基于MFD的区域双层边界协调控制研究
2017-08-10刘娜傅惠
刘娜,傅惠
(广东工业大学机电工程学院,广州 510006)
基于MFD的区域双层边界协调控制研究
刘娜,傅惠
(广东工业大学机电工程学院,广州 510006)
提出一种基于宏观基本图(MFD)的城市区域双层边界交通协调控制策略。上层以网络输出量最大和延误时间最小为目标,采用模型预测控制算法进行优化求解得到区域控制参数;下层分解实现区域边界控制参数,使各子区拥堵均衡化。用MATLAB进行数值仿真,对不同控制策略下的交通拥堵状况进行对比分析。经验证:所提出的控制策略可有效地协调各子区流量,缓解交通拥堵,提高整个路网的性能。
0 引言
国内大中城市面临交通拥堵和大气污染两大城市问题,而这两大难题都与城市交通有关。目前,缓解城市交通拥挤的问题,主要有两个方法:一是加强交通基础设施建设,适应高速增长的交通需求;二是对交通流进行科学的组织与管控,充分发挥现有交通网络的通行潜力,最大程度上使交通流有序流动。由于智能交通是一个复杂的系统,解决城市交通问题不能单靠扩建道路来达到预期效果。如何利用已有的道路基础设施,通过交通控制、交通诱导等手段,对在途交通流进行合理的控制、管理,以实现出行交通流(需求)在有限路网(供给)中的合理时空分布,从而减少甚至避免交通拥堵更具有现实意义,也已成为广大学者普遍关注的问题。
基于上述情况,本文提出一种基于宏观基本图(MFD)的城市区域双层边界交通协调控制策略。以宏观交通基本图作为路网的性能表征工具,实现对各子区边界入口的流量控制(即边界控制)。这样就将问题描述层次,从路口级提升到子区级,从而降低了问题描述的复杂度,也降低了对路网完备交通数据的要求。
1 基于MFD的城市交通网络系统
1.1 区域MFDs系统
我们将一个车辆密度分布不均衡的城市CBD交通网络划分为2个区域RI,I=1,2,如图1所示,R1为中心保护区,R2为外围区。对于两个区域的交通系统而言,有两种内部交通需求D11(t)和D22(t)[veh/s]分别产生于区域R1和区域R2;一种外部交通需求D21(t)[veh/s],以 R2为起点,R1作为终点的交通需求。相对于这3种交通需求,车辆交通状态也对应分为 3类 N11(t)、N22(t)、N21(t)[veh/s]。 NIJ(t)表示 t时刻,区域RI中以区域RJ为目的地的车辆数。NI(t)[veh]表示t时刻,区域 RI中总的车辆数,即
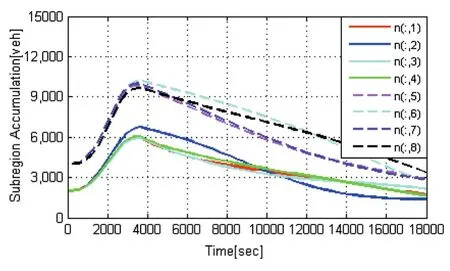
对于划分后的每个区域RI都有一个界限清晰、分散度较低的MFD,用来反映该区域中移动车辆总数NI(t)与该区域的完成流GI(NI(t))[veh/s]之间的关系。所谓区域完成流,即该区域与邻区间的转移流与该区域内部转移流之和。相邻区域R1和R2间的流量转移由设置在区域边界路口的区域边界控制器U(t)(其中0 图1 区域MFDs系统 我们假设同一区域内所有车辆的行驶距离相同(即不考虑车辆在区域内的起始点、目的地与行驶路径的不同而造成的行驶距离的差异),那么区域转移车流量与区域输出车流量满足如下公式: 1.2 子区MFDs系统 为了减小上述区域内车辆密度分布的不均衡性,我们将上述保护区R1和外围区R2再次划分成8个子区SRi,i=1, 8,如图2所示。对于子区交通系统,qij(t)[veh/s]表示t时刻从子区SRi到子区SRj的交通流需求;nij(t)[veh]则对应为t时刻子区SRi中以子区SRj为目的地的车辆ni(t)[veh]为t时刻子区SRi中总的车辆数,即。对于划分后的每个子区SRi同样都有一个界限清晰、分散度较低的MFD,用来反映该子区中移动车辆总数ni(t)与该子区的完成流之间的关系。用表示从子区SRi中以SRj为目的地转移到子区SRh中的车流量,其中 i≠j,h∈ξi,ξi表示子区 SRi的相邻子区集合。mij(t)[veh/s]表示t时刻从子区SRi转移到子区SRj的交通流,。每组相邻的两个子区间都存在一个子区流量控制器uij(t),0 图2 子区MFDs系统 由于子区MFDs系统的控制目标是:1)协调各子区间的车流量,使得拥堵均衡化;2)分解实现区域边界控制参数U(t)。因此,子区流量控制器分为两个类型:1)子区边界控制器uPFC,设置在中心区与外围区边界处的两个相邻子区间(这两个子区分别属于不同的区域),用于分解实现区域边界控制器U的控制作用,通过协调边界子区间流量的交换来达到协调中心保护区与外围区间的流量转移;2)子区内部控制器uIFC,设置在同一区域内的两个子区间,用于协调同一区域内相邻子区间的交通流,使该区域内各子区拥堵状况均匀化,从而使整个区域交通性能处于最优状态。 2.1 宏观基本图概述 MFD(即宏观基本图)正式定义由Daganzo和Geroliminis于2008年给出[1]。认为MFD是道路网络的基本属性,可以描述网络中移动车辆数和网络运行水平之间的普遍关系,独立于交通外部需求。Daganzo提出MFD的概念后,通过日本横滨等地的实地数据采集与阿姆斯特丹等城市的仿真研究,验证了城市路网中MFD的存在[2,3-5]。通过对实地的数据采集、处理与流量散点图分析研究,Daganzo认为MFD为三角形[3]。马莹莹通过VISSIM仿真,发现当网络内交通流量在一定范围内时,区域中的输出车辆数保持不变,即其图形类似一个梯形[6]。 为了得到区域的MFD图,我们需要对经过预处理的交通检测器采集的数据进行加权处理,以表示区域级的交通状态参数,其加权公式如下所示: 其中:Ri表示区域i,Gi和Ni分别代表区域i的加权流量和总的车辆数,qr和or分别表示路段r上用检测器检测得到的车流量和时间占有率,Lr和lr为路段r的车道数和路长,s为平均车长(一般取s=5米)。 MFD除了可以通过仿真和实际数据获取,还可以通过数学解析模型来构造。Daganzo等[7]利用旧金山网络数据提出了一个精确的分析表达式来表达MFD,如下公式(4)所示: 其中:Gi(Ni(t))和Ni(t)分别表示t时刻,区域i的总的输出量和总的车辆数,A1、A2、A3、A4为常数,由实际路网决定。 2.2 非均匀性对MFD影响研究 研究表明,实际路网中由于时空拥堵的不均匀性,网络中存在“滞回现象”[8-9]。所谓“滞回现象”是指所采集的数据在流量与占有率比例关系图形中构成封闭曲线,而不是线性曲线。而引发这种现象的主要原因是由于交通路网中车辆密度分布的不均匀性和采集数据量的不足。 为了研究交通网络中车流密度分布的不均匀性对MFD的影响,本文基于广州市天河区的交通检测数据进行交通网络的密度不均匀性分析研究。研究选取的交通网络地图如图3所示,检测数据为2015年3月、4月、5月的数据,数据采集时间间隔为30秒,为了避免城市交通中的间断流现象造成的数据的巨大波动,这里,我们采用5分钟的间隔进行采集数据的处理。 图3 不同平均占有率与占有率标准差下的网络平均流量 如图3所示,平均占有率表征为交通网络拥堵水平的指标,占有率标准差为权衡交通网络不均匀性的指标。由图3可知,当网络平均占有率值较小(即网络交通状况畅通)时,交通网络平均流量与占有率标准差成正比例关系,此时整个网络处于畅通状态。当车辆数增加到一定程度时,占有率标准差不断增大,车流密度分布的不均匀性开始对交通网络性能产生影响,从而使得网络平均流量与占有率标准差呈现反比例关系。当网络整体拥堵水平达到20%时,网络平均流量开始不受网络密度不均匀性的影响。Mazloumian的研究中也曾得出相似的结论,认为当网络较通畅时,网络平均流量与网络不均匀性成反比例关系,而当网络拥挤水平达到50%时,网络平均流量将不再受网络车流密度分布不均匀性的影响[10]。 然而,我们不能认为此现象为交通网络中的普遍现象,因为我们的研究中还存在一些缺陷。如我们检测器的覆盖率并没有达到100%,所以我们的研究数据的不足可能会使我们的分析产生偏差。但是,不论该现象是否普遍,由于“磁滞现象”的存在,空间密度分布不均匀的交通网络所呈现出来的网络流量小于那些近些满足均匀条件(道路密度偏差小)的网络流量[11,12]。这里,我们将不均匀性的影响考虑到MFD的函数解析式中为: 式中,A1、A2、A3、A4为常数,由实际路网确定;SDi(t)为区域Ri的占有率标准差;Err(t)为拟合误差。 3.1 上层区域边界控制 该层控制目标是使网络车辆延迟最小化的同时输出量最大。这里我们采用模型预测控制算法进行优化建模,并使用遗传算法进行求解。模型预测控制算法在均匀交通网络的边界控制策略中的应用可参考文献[13-14]。 交通网络中车辆总延误时间为网络中所有移动车辆的在途行驶时间,可表示为: 交通网络中系统整体输出量可看作是网络中所有到达目的地的车流量的总和,可表示为: 对于整个交通网络系统而言,各区域的车辆数不能超过区域的最大容量值,边界控制参数不能超出其给定的上下限。故上述所述交通区域网络系统整体优化目标函数可表示为: 3.2 下层子区协调控制 上层区域边界控制的主要目的是为了使网络总体延迟最小化。然而,这种控制方法是在假设网络拥堵水平均匀的基础上提出的。对于实际不均匀性路网,直接应用这种控制方法并不是最优的。因此,这节我们将介绍一种子区流量控制器,通过调节子区间的控制参数协调个子区间的车辆数,使各子区间的拥堵均匀化,从而改善整个交通网络的性能。下层子区间车流量协调的依据主要是使同一区域内各子区车辆数均匀化并处于使子区性能最优处(即MFD中的临界车辆数),这里,我们取预测时域Kp内的平均车辆数为控制步长kc时区域的理想车辆数: 则该区域内各子区的理想车辆数由各子区容量在该区域内的比值确定: 其中,θi为子区SRi在所属区域中所占容量比值;χ为子区流量控制器判断标志,χ=1表示子区内部控制器,χ=0表示子区边界控制器。 则子区流量控制器计算公式为: 为了验证上述模型的有效性,本文对其进行MAT⁃LAB数值仿真验证。仿真路网为上文提到的广州市天河区交通路网,整个仿真时段取18000秒,仿真样本时间为300秒,预测时域为20,区域车流量初始值为具体仿真测试分为“无控制”、“常数参数控制”和“区域双层边界控制”三种方案。“无控制”方案中,不对区域之间流量的交换进行控制,即边界控制参数u=1;“常数参数控制”方案中,将所有边界控制参数设定为一个统一的常数,这里我们取0.5。仿真结果如图4、图5、图6所示: 图4 无控制策略下各子区车辆变化 图5 常数控制策略下各子区车辆变化 从仿真结果可知,对于“无控制”的交通区域网络系统,子区5、6、7、8在不同仿真时刻达到最大车辆容量,分别为 1500辆、1400辆、1500辆、1100辆,子区内发生交通阻塞,如图4。而对于“常数参数控制”的交通区域网络系统,只有子区2在仿真疏散后期发生交通阻塞,车辆数达到其最大容量值9000辆,如图5。图6为实施本文提出的基于MFD的区域双层边界协调控制策略的仿真效果图,所有子区整个过程都没有达到拥堵阻塞状态,在仿真过程中,各子区车辆数一直处于相对均衡状态。通过不同控制策略下的仿真结果进行比较,发现所提出的基于MFD的区域双层边界协调控制策略起到了均衡交通流量,减少延误时间,改善交通网络性能的作用。 图6 区域双层边界控制策略下各子区车辆变化 本文紧密结合城市交通控制系统的特点,借助宏观基本图(MFD)作为交通路网的性能表征工具,并将其用于交通控制与诱导的优化建模,使得区域交通控制策略复杂度与计算量大大降低。基于采集的实时交通数据将网络的非均匀性对区域MFD形状的影响进行分析,并得出MFD函数解析式。提出基于宏观基本图(MFD)的城市区域双层边界交通协调控制策略,给出系统优化模型,并用实际数据进行MATLAB数值仿真验证了该控制方法的有效性。本文的研究工作为城市智能交通控制系统的发展提供了理论与技术支持。 [1]Ampountolas,K.,Zheng,N.and Geroliminis N..Perimeter Flow Control of Bi-modal Urban Road Networks:A Robust Feedback Control Approach.European Control Conference:9-14,2014. [2]Geroliminis N.,Daganzo C.F..Existence of Urban-scale Macroscopic Fundamental Diagrams:Some Experimental Findings.Transportation Research Part B,2008,42(9):759-770. [3]Daganzo C F.Urban gridlock:Macroscopic Modeling and Mitigation Approaches[J].Transportation Research Part B Methodological,2007,41(1):49-62. [4]Cassidy M J,Jang K,Daganzo C F.Macroscopic Fundamental Diagrams for Freeway Networks:Theory and Observation[J].2011,2260(-1):8-15. [5]Geroliminis N,Daganzo C F.Macroscopic Modeling of Traffic in Cities[C].Transportation Research Board 86th Annual Meeting,2007. [6]马莹莹.面向交通小区的交通控制策略研究[M],2009. [7]Daganzo C F,Geroliminis N.An Analytical Approximation for the Macroscopic Fundamental Diagram of Urban Traffic[J].Transportation Research Part B Methodological,2008,42(9):771-781. [8]Geroliminis,N.and Sun J..Hysteresis Phenomena of A Macroscopic Fundamental Diagram in Freeway Networks.Procedia-Social and Behavioral Sciences,2011,17:213-28. [9]Geroliminis,N.,Sun,J.,2011b.Properties of A Well-defined Macroscopic Fundamental Diagram For Urban Traffic.Transportation Research Part B 45(3),605-617. [10]Ramezani M,Haddad J,Geroliminis N.Dynamics of Heterogeneity in Urban Networks:Aggregated Traffic Modeling and Hierarchical Control[J].Transportation Research Part B Methodological,2015,74:1-19. [11]Mahmassani,H.S.,Saberi,M.,Zockaie,A.,2013.Urban Network Gridlock:Theory,Characteristics,and Dynamics.Transportation Research Part C:Emerging Technologies 36,480–497. [12]Knoop,V.,Hoogendoorn,S.,van Lint,H.,2013.The Impact of Traffic Dynamics on the Macroscopic Fundamental Diagram.In:92nd Annual Meeting of Transportation Research Board.Washington,DC,USA. [13]Geroliminis,N.,Haddad,J.,Ramezani,M.,2013.Optimal Perimeter Control for Two Urban Regions with Macroscopic Fundamental Diagrams:A Model Predictive Approach.IEEE Transactions on Intelligent Transportation Systems 14(1):348-359 [14]Haddad,J.,Ramezani,M.,Geroliminis,N.,2013.Cooperative Traffic Control of a Mixed Network with Two Urban Regions and a Freeway.Transportation Research Part B 54:17-36 Research on Hierarchical Perimeter Control Based on Macroscopic Fundamental Diagram LIU Na,FU Hui To alleviate urban traffic congestion,proposes a hierarchical perimeter control strategy for regional urban traffic based on the Macroscopic Fundamental Diagram(MFD)to improve the effectiveness of the whole network.In the high-level,adopts the model predictive control ap⁃proach to solve the optimal control problem such that the network total delay is minimized and the network capacity is maximized,and cal⁃culates the regional optimal control inputs.In the low-level,the goal of the subregional controller is to realize regional optimal control in⁃puts and minimize the regional heterogeneity.Presents several numerical simulations with MATLAB to verify the effect of the proposed hi⁃erarchical perimeter control strategy.Simulation experiments show that the proposed control strategy can effectively coordinate the each subregional traffic flow and improve the network performances so as to alleviate urban traffic congestion. 国家自然科学基金(No.6157020428) 刘娜(1992-),女,湖北荆州人,硕士,硕士,研究方向为智能交通研究 2017-03-31 2017-06-10 1007-1423(2017)17-0010-06 10.3969/j.issn.1007-1423.2017.17.002 宏观基本图;边界控制;非均匀性;模型预测控制 傅惠(1981-),男,湖北荆州人,副教授,博士,研究方向为智能交通系统 Macroscopic Fundamental Diagram;Perimeter Control;Heterogeneity;Model Predictive Control


2 网络非均匀性对MFD的影响

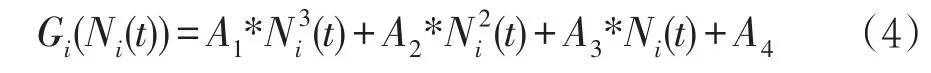


3 区域双层边界协调控制模型


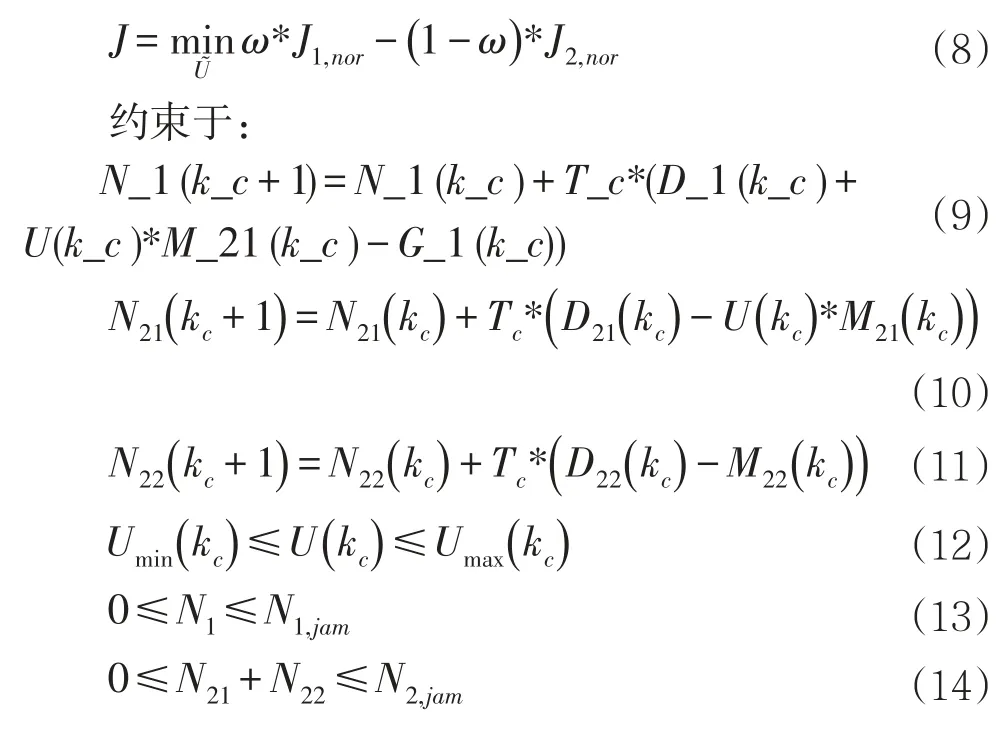


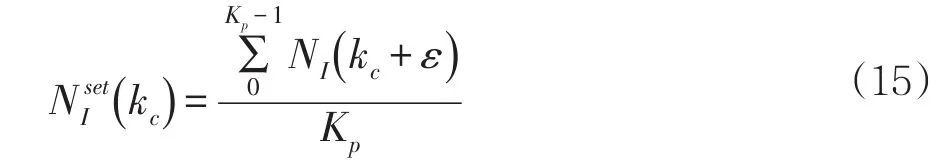


4 仿真验证


5 结语
(School of Electromechanical Engineering,Guangdong University of Technology,Guangzhou 510006)
