基于LuGre摩擦理论的动态轮胎模型研究

李胜琴，赵银宝

(东北林业大学 交通学院， 哈尔滨 150040)



基于LuGre摩擦理论的动态轮胎模型研究

李胜琴，赵银宝

(东北林业大学 交通学院， 哈尔滨 150040)

基于LuGre动态摩擦理论，建立了用于研究车辆动力学特性的动态轮胎模型，推导了车辆轮胎纵向力和侧向力的表达式，以此作为基础进行整车动力学的模拟仿真。采用遗传算法对轮胎模型中的稳态及动态参数进行辨识，比较分析了模型参数对模型精度的影响。利用Matlab/Simulink建立起自由度整车动力学模型，通过进行转弯制动仿真来对本文所建立的轮胎模型进行了验证。结果表明：本文所建立的动态轮胎模型准确度较好，能够用于车辆动态性能仿真研究。

LuGre摩擦理论；轮胎模型；整车模型

轮胎作为车辆重要的组成部分，是车辆和路面接触的唯一载体，轮胎的力学特性对汽车的操纵稳定性、动力性以及制动安全性有着极其重要的影响，是研究和分析车辆动力学性能的基础[1]。车辆在行驶过程中，所受到的外力绝大部分来源于车轮和路面间的相互作用[2]，因而在对车辆进行系统动力学仿真研究时，轮胎的力学特性，尤其是动态运动过程中的运动特性研究则至关重要。

在目前的轮胎仿真中，稳态轮胎模型可以很好地拟合轮胎试验数据，简化分析和计算过程，从而得到了广泛的应用。但是稳态模型是在高度控制的实验室条件下得到的，不能及时捕捉到轮胎的动态特性，而在LuGre轮胎动力学摩擦模型中，轮胎和地面间接触摩擦力的变化状态可以通过对时间的微分方程体现出来，并利用摩擦理论来描述轮胎和路面间的接触摩擦。因此，该模型可准确描述轮胎和路面之间的摩擦力，实现对车辆转向制动等行为的实时控制。

1995年，Canudas 等[3]以刷子模型为基础，推导出轮胎动力学摩擦模型，称为“LuGre动力学摩擦模型”，该模型引入一个变量来对轮胎内部的摩擦状态进行表示，然后结合该变量对时间的微分共同来描述轮胎与路面之间的摩擦，因此可准确地对轮胎与路面之间的摩擦效应进行表达。2002年，E.Velenis 等[4]扩展了LuGre模型，使得该模型可以准确地描述轮胎的纵向以及侧向受力行为。2004年，J.Deur等[5]考虑到轮胎模型参数和法向载荷之间的关系，对LuGre轮胎模型进行了改进，使得LuGre轮胎模型能更方便地用于车辆模型仿真和控制。

1 LuGre动态轮胎模型

LuGre轮胎模型主要有两种表达形式，即集中式轮胎模型和分布式轮胎模型，前者设定轮胎和路面是点接触，用常微分方程表示，对时间进行积分即可求解；后者设定轮胎和路面是面接触，用偏微分方程来表示，需要在时间和空间上都积分才可求解[6]。

分布式LuGre轮胎模型示意图如图1所示，将轮胎和路面接触的区域简化为矩形，应用微分理论，设接触面的长度为L，认为接触面由一系列的单元组成，每个单元所受的摩擦力用一阶模型来表示。

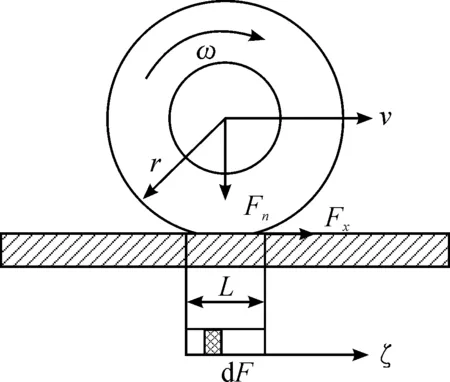
图1 分布式LuGre轮胎模型

模型的数学表达式如式(1)～(3)所示：

(1)

(2)

(3)

式中：fn(ζ)为轮胎接地印迹方向上的压力分布函数；σ0为轮胎纵向刚度系数；σ1为轮胎纵向阻尼系数；σ2为轮胎相对黏滞阻尼系数；z为轮胎平均弹性形变量；θ为不同路面的摩擦因数，在冰、雪、湿沥青路面、干沥青路面上，取值依次为0.1、0.2、0.6、0.8；F为轮胎的摩擦力；Fn为轮胎受垂直载荷；μc为库仑摩擦因数；μs为静摩擦因数；通常认为μc≤μs。

基于LuGre分布式摩擦模型的工作原理，借助准确的车辆动力学模型，建立起能够描述车辆摩擦状态的表达式，有利于后续对路面附着状态进行实时估计和对车辆主动安全性控制策略展开研究。

2 模型参数分析

作为车辆和路面唯一接触的部分，轮胎的纵滑特性和与路面的附着特性会影响到车辆行驶中的驱动及制动性能，通常用μ-s曲线(轮胎/路面摩擦因数和滑移率曲线)来描述轮胎和地面附着性的好坏[7-8]。由于路面和轮胎自身的特性在运动过程中不断变化，导致系统的模型参数发生变化，因此有必要对模型参数进行分析。

根据LuGre分布式轮胎模型，推导出轮胎模型μ-s关系式为：

(4)

(5)

(6)

其中滑移率s∈(0,1)。

在研究模型中的某一个参数变化对滑移率的影响时，假设其余的参数不会发生变化，模型μ-s曲线的变化只随单参数发生变化，由于轮胎纵向阻尼系数σ1对μ-s曲线无影响，本文选取剩余几个模型参数和路面条件的变化，对参数值附近的几个点进行比较分析。

轮胎模型取不同库仑摩擦因数和不同静摩擦因数时对μ-s的曲线影响如图2所示。可以看出，μc对μ-s曲线的影响主要集中在滑移率为0.2～1时，对较低滑移率(0～0.1)之间的影响很小，μs主要影响中低滑移率时摩擦因数的数值，随着数值的增加，峰值摩擦因数逐渐增大，整体曲线都呈现上移的趋势；对于图2(a)，摩擦因数的差值最大在0.2，由于车辆在正常行驶时，滑移率通常维持在较低的范围，此时的摩擦因数差别不大。图2(b)摩擦因数的差值变化控制在0.1之间，所以μc、μs对模型的精度影响比较小。

当轮胎模型其他参数取值不变，轮胎纵向刚度系数发生变化时，对μ-s曲线产生的影响如图3所示，可以看出，轮胎纵向刚度系数的变化主要影响摩擦因数峰值的变化，对滑移率0.1～0.3范围内影响比较集中。随着σ0取值的增大，峰值摩擦因数变大，但是相对的滑移率数值有减小的趋势。此外，在中高段滑移率时，μ-s曲线基本重合。轮胎纵向刚度系数对于摩擦因数造成的误差很小，最大在0.05，σ0对于模型的精度影响最小。

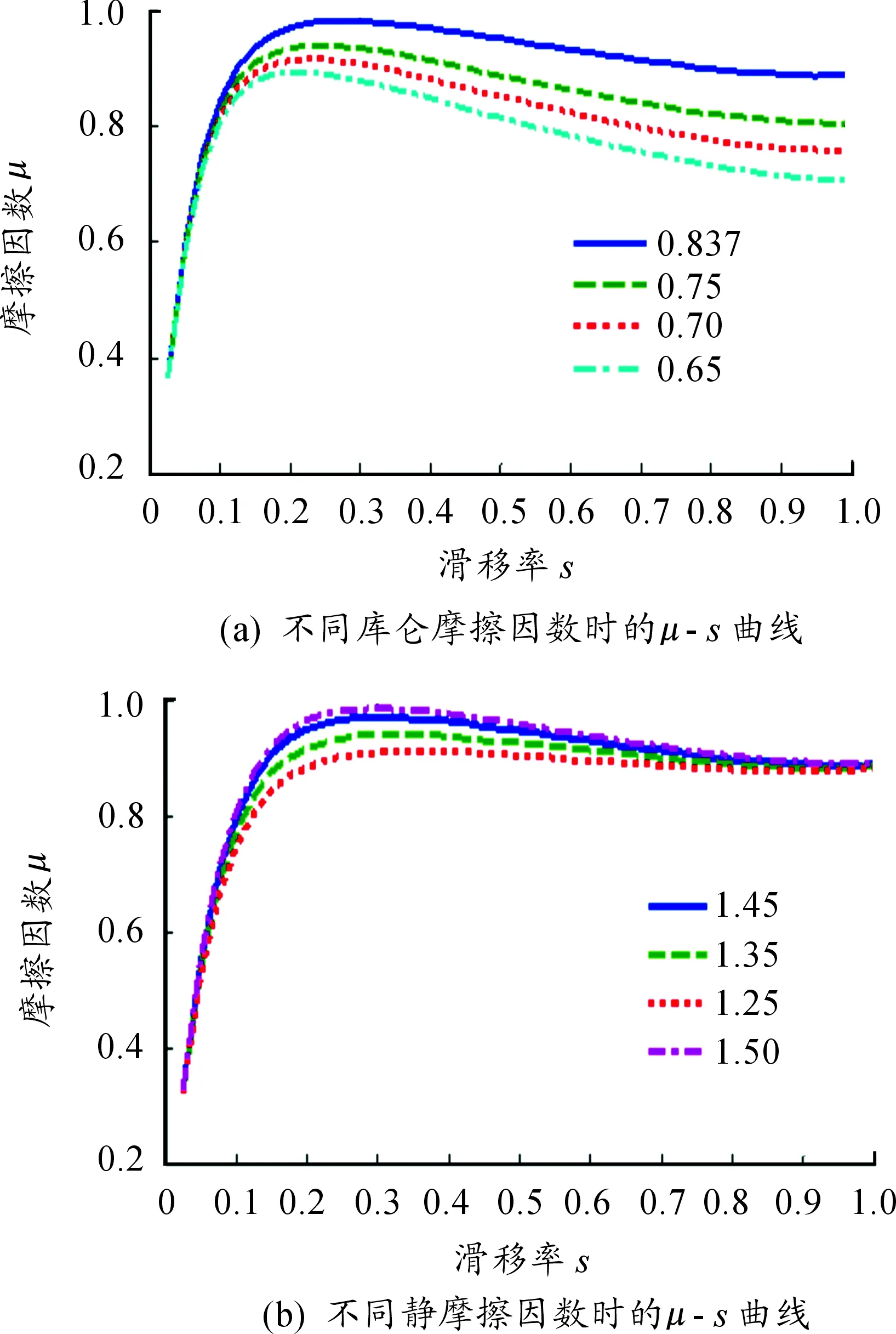
图2 μc、μs对μ-s曲线的影响

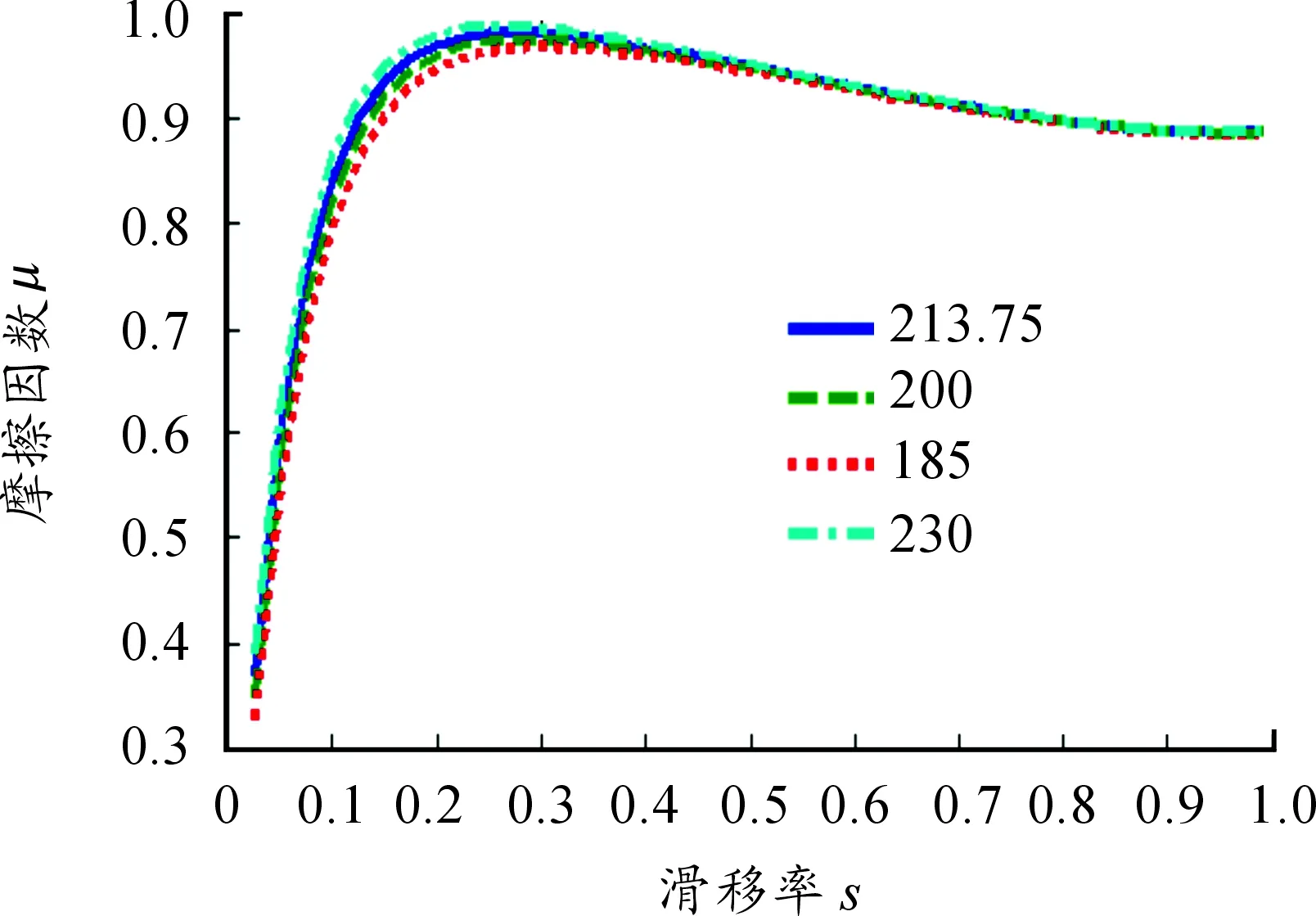
图3 σ0对μ-s曲线的影响

轮胎/路面间附着系数θ在冰、雪、湿沥青路面、干沥青路面取值依次为0.1、0.2、0.6、0.8，不同的路面条件对于μ-s曲线的影响如图4所示，可以看出，摩擦因数受路面条件的影响非常大。当路面附着系数逐渐增大时，对应的摩擦因数的峰值增加较快，并且峰值系数对应的滑移率数值向左偏移，μ-s曲线整体趋势向上偏移，且幅度比较大，μ-s曲线对路面的敏感性强，整体变化趋势符合实际试验结果。

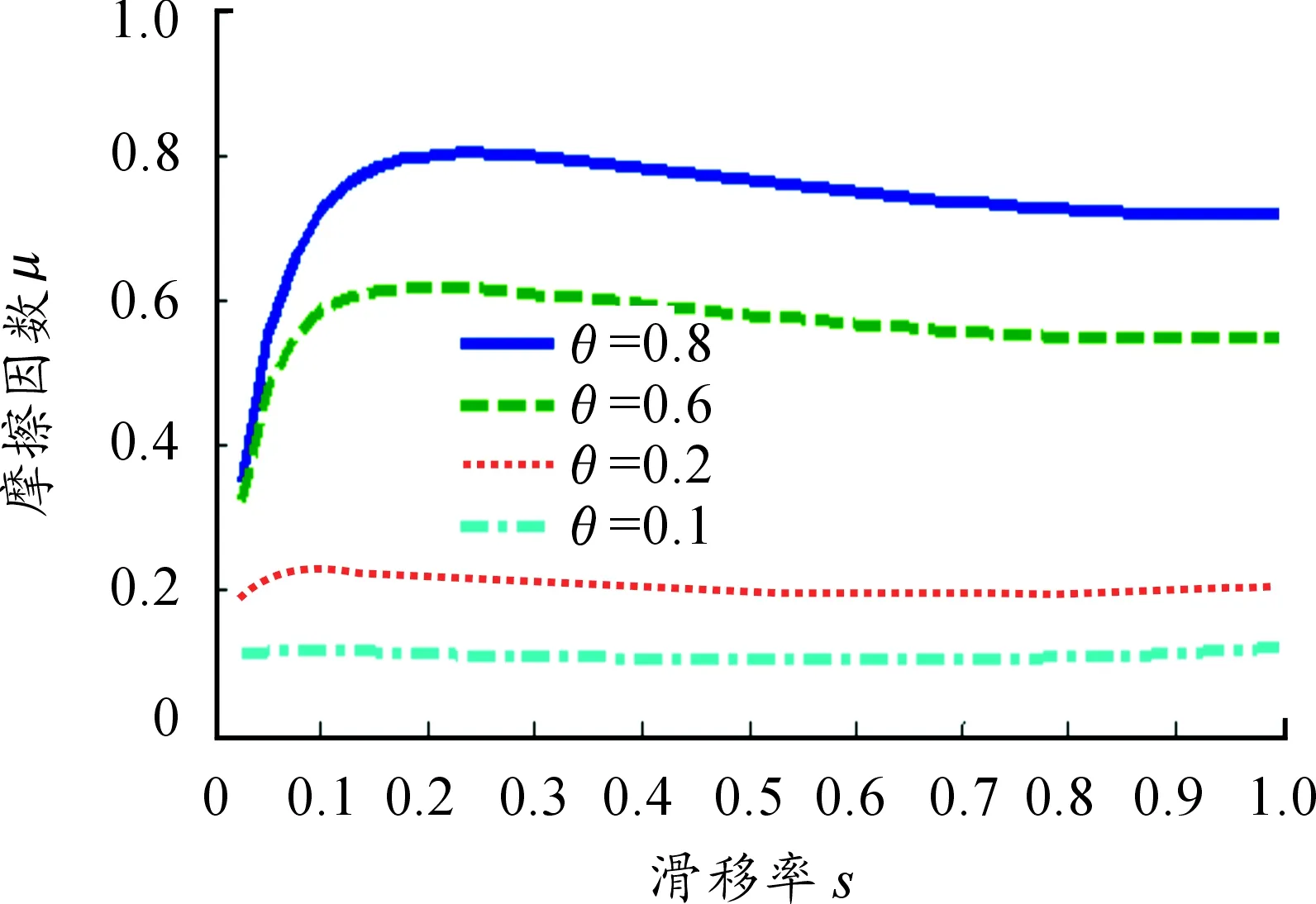
图4 不同路面条件时的μ-s曲线

综合以上的模型参数分析，可以得出，LuGre轮胎模型的参数拟合误差对于模型的预测结果影响不大，根据经验选取一组参数来计算轮胎的纵向力和侧向力。

3 LuGre轮胎模型的应用

车辆系统动力学把车辆看作是一个动态系统，研究车辆在受到力以及力矩作用时的动态响应特性，然后分析响应特性对车辆各种性能的影响。本文拟建立整车七自由度仿真模型，选择转弯制动作为试验工况，对整车运动变化进行仿真分析。

3.1 动力学模型

为了研究方便，对车辆实际运动状态进行一定简化：前轮转角直接施加在车轮上；转向系统是刚性的，有固定的传动比，输入通过转向盘施加给车轮；不考虑悬架的作用，认为车辆不受垂向路面不平激励；左右前轮转角相同；车辆绕x轴的侧倾角和绕y轴的俯仰角为零；车辆的4个轮胎的特性都相同；不考虑空气阻力以及滚动阻力对车辆造成的影响[9-10]。基于以上假设条件，简化后的车辆动力学模型如图5所示。

根据牛顿定律建立的车辆的横摆运动、纵向及侧向运动的动力学方程如式(7)～(9)所示。

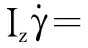
(7)

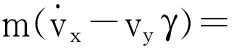
(8)

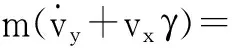
(9)

车辆4个车轮的转动动力学方程如式(10)所示：

(10)

式中：m为整车的质量；vy为车辆的侧向速度；vx为车辆的纵向速度；γ为车辆的横摆角速度；δ为前轮转角；Iz为整车绕z轴的转动惯量；Fxi为4个车轮的纵向力，其中i=fl,fr,rl,rr；Fyi为4个车轮的侧向力；wi为4个车轮的角速度；Tbi为4个车轮上的制动力矩；Jw为轮胎的转动惯量；a为质心到前轴的距离；b为质心到后轴的距离；d1为前轴轮距；d2为后轴轮距；R为车轮的滚动半径。

图5 简化后的车辆动力学模型

本文将轮胎和路面的接触简化为仅在二维平面的运动，此时研究的二维LuGre轮胎模型需要用到的坐标系如图6所示。

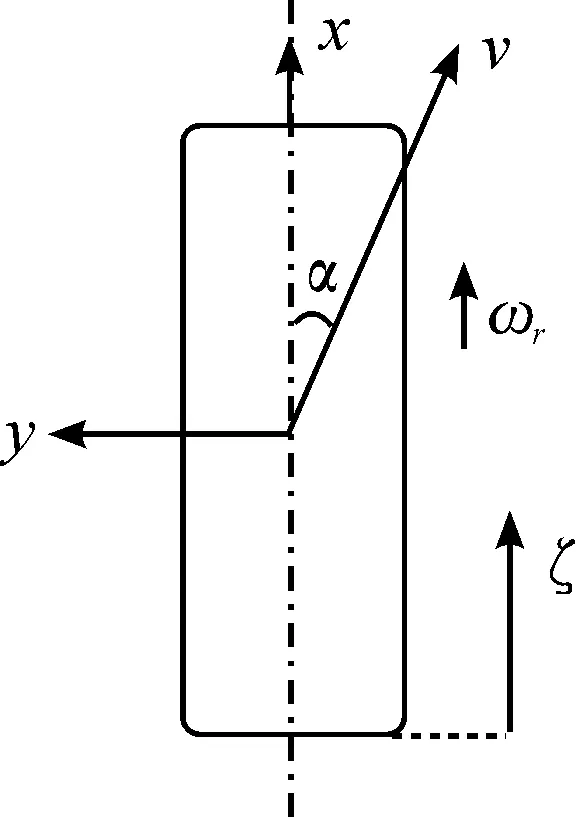
图6 LuGre轮胎模型坐标系

轮胎和路面的接地印记是矩形，设其长度是L，宽度为W，假设该矩形接触面是由无数个微小单元体组成，每个单元体都具有二维LuGre轮胎模型的特性。该坐标系中，r为轮胎的滚动半径，ω为车轮的角速度，v为车轮前进速度，α为车轮侧偏角。把纵向和侧向的相对运动速度分别定义：

(11)

则车辆动力学模型中，轮胎与路面之间的纵向力、侧向力可用式(12)表示：

(12)

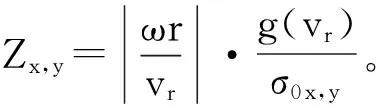
3.2 整车模型初步仿真

根据以上公式，在Matlab/Simulnk中建立整车动力学模型，对其进行转弯制动仿真分析，通过车辆运行状态的变化趋势，来研究车辆的转弯制动特性。让车辆以速度为54 km/h(15 m/s)的速度匀速前进，在1 s时，设定前轮转角输入为5°，如图7(a)所示，查阅资料得角传动比为18，此时的方向盘转角为90°；给4个车轮相同的制动力矩，大小是600 N·m，如图7(b)所示，假设在转弯制动的瞬间，车辆驱动力矩突变为零。具体的参数数值见表1。

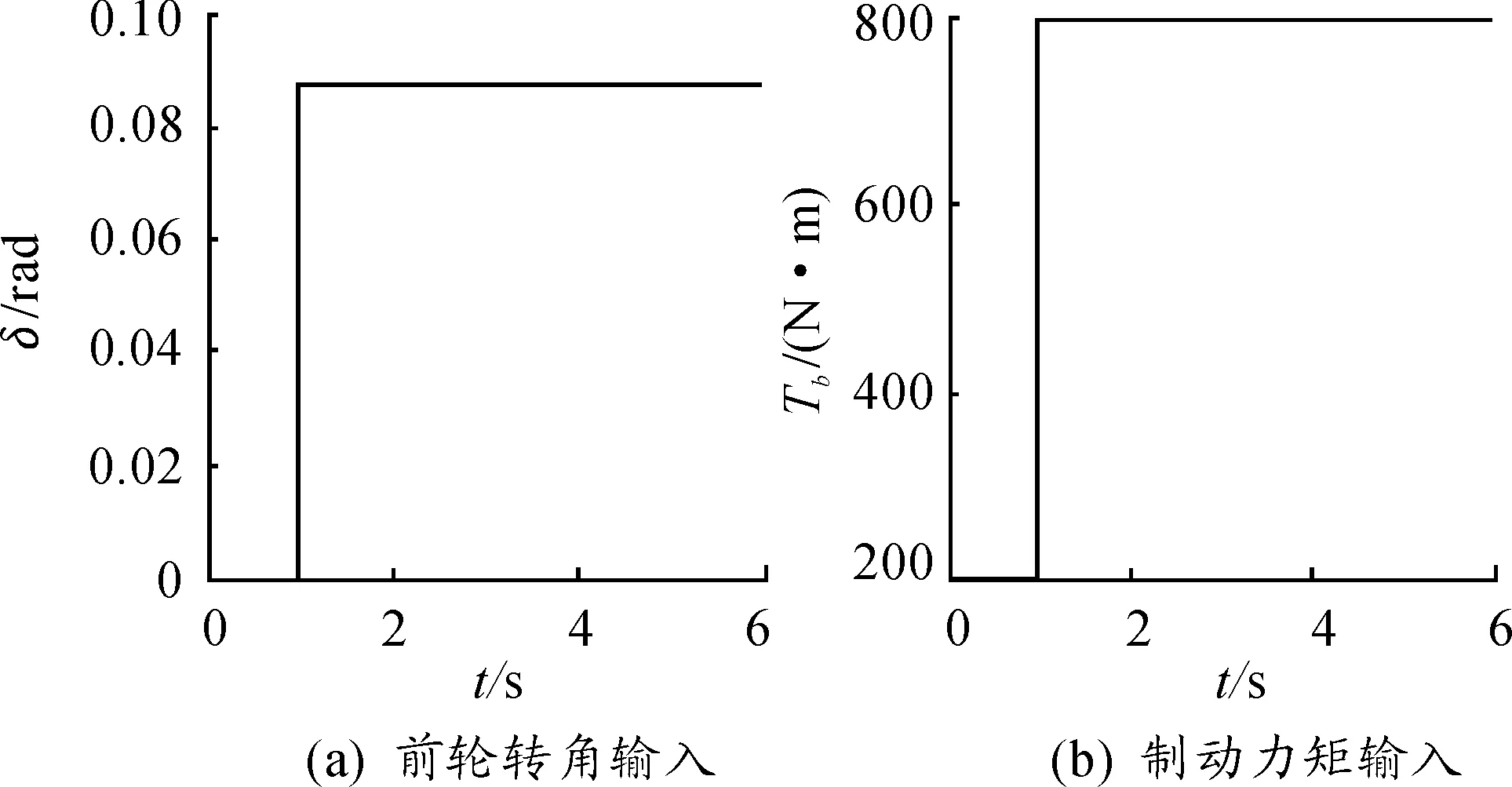
图7 仿真输入条件

本文选取了几个能用来描述车辆运动特性的性能指标，进而对车辆的运行状态进行分析。

车辆在转弯制动过程中纵向速度和侧向速度随时间的变化趋势如图8所示，可以看出，车辆的纵向速度减小直至车速减为零，根据曲线的斜率可以推导出纵向减速度在转弯开始的瞬间最大，然后逐渐减小；侧向速度在转弯开始时瞬间增大到最大值，然后减小，发生波动，最后数值为零，车辆停止，在这个过程中，曲线呈现出波浪形变化，不同于采用稳态轮胎模型时的仿真曲线，这是LuGre轮胎模型仿真曲线的特点。

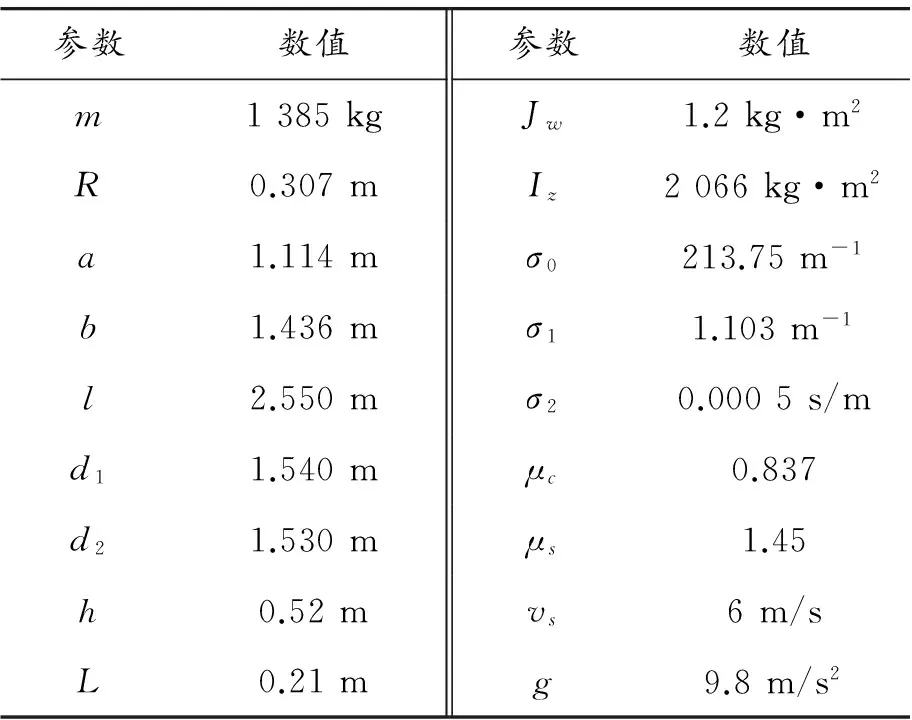
表1 整车参数

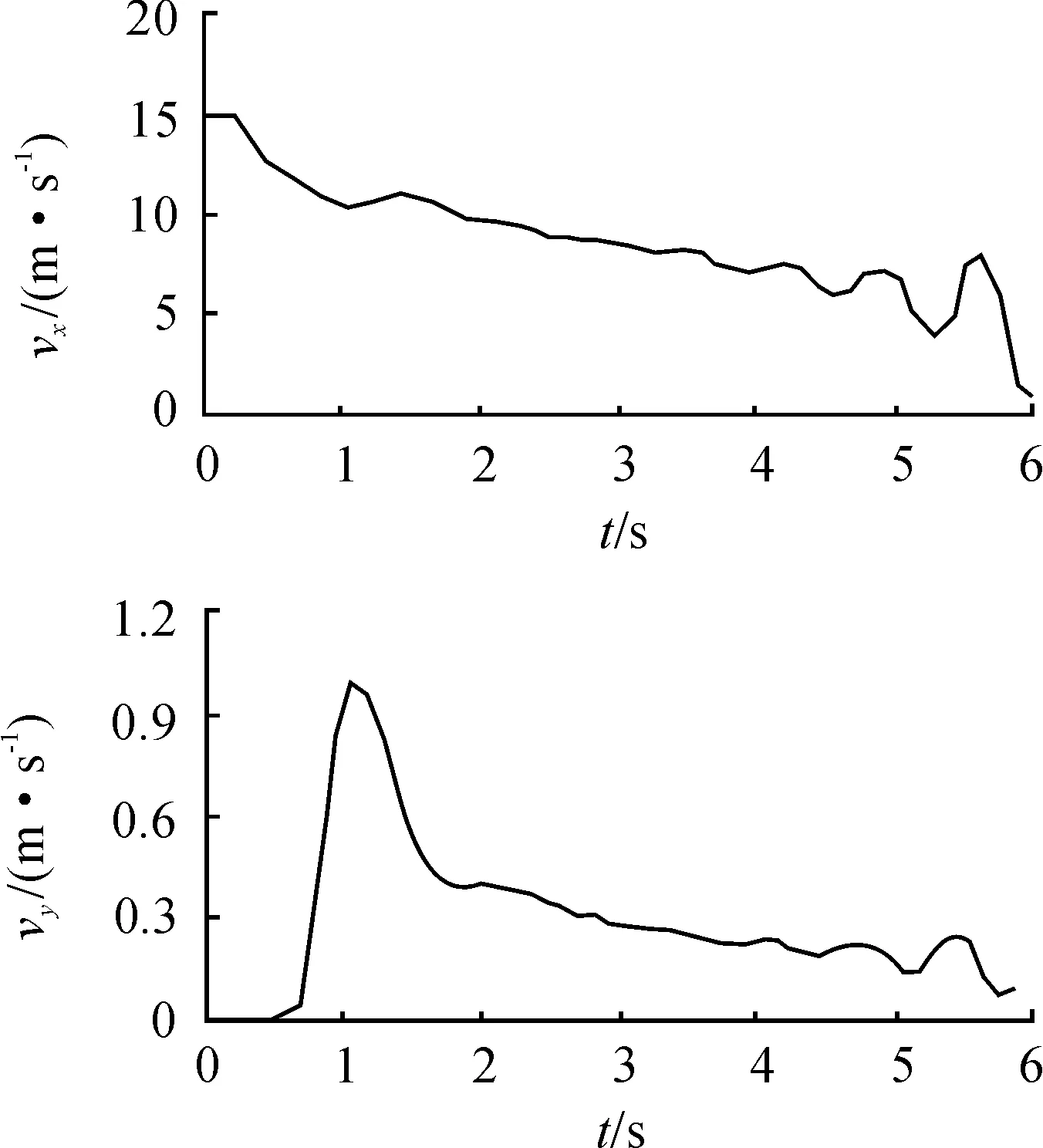
图8 纵向速度和侧向速度随时间变化曲线

横摆角速度和质心侧偏角随时间的变化趋势如图9所示，在转弯开始的瞬间，前轮输入导致横摆角速度增大，到达最大值后随着车速的降低而相应减小；由于车轮侧偏角的产生导致质心侧偏角有一定的波动，质心侧偏角逐渐增大，后期随着时间的延长其变化不再明显，车辆不会再发生大的波动。在这个过程中，曲线具有轻微的波动性，同样体现出轮胎的动态特性，证明本文研究的动态轮胎模型是适用的。

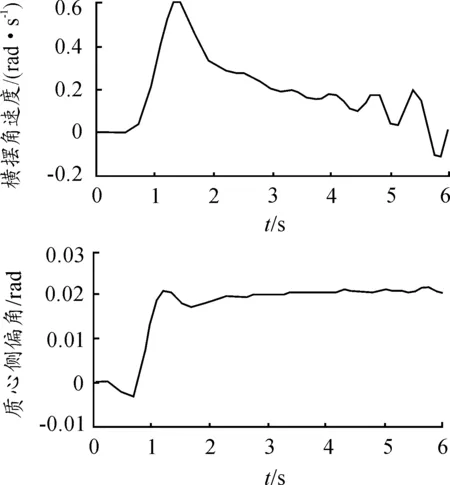
图9 横摆角速度和质心侧偏角随时间变化曲线

4 结论

1) 基于LuGre动态摩擦理论，建立用于车辆动力学特性研究的LuGre动态轮胎模型，并对其库仑摩擦因数、静摩擦因数、轮胎纵向刚度、纵向阻尼系数等关键参数进行了辨识；选择几组不同参数进行比较分析，结果表明所辨识参数精度较高，能用于LuGre轮胎模型的应用研究。

2) 建立包含LuGre轮胎模型在内的七自由度整车动力学模型，应用该模型对车辆转弯制动过程进行了仿真研究，选取车辆横摆角速度等具有代表性的运动参数进行比较。结果表明，参数的变化趋势符合车辆转弯制动过程的运动特性，该轮胎模型能用于车辆动力学仿真研究。

[1] 袁忠诚.轮胎稳态模型研究[D].长春：吉林大学,2006.

[2] 郑文刚，陆永婕，陈恩利，等.基于ADAMS/MATLAB联合仿真的LuGre动态轮胎模型研究[J].动力学与控制学报,2016,14(3):247-252.

[3] 张淼.LuGre轮胎模型与车辆动力学软件的接口研究和实现[D].西安：长安大学,2014.

[4] VELENIS E,TSIOTRAS P,de WIT C C.Extension of the LuGre Dynamic Tire Friction Model to 2D Motion[J].Proceedings of the 10th Mediterranean Conference on Control and Automation.2002.

[5] DEUR J,ASGARI J,HROVAT D.A 3D Brush-type Dynamic Tire Friction Model[J].Vehicle System Dyna-mics,2004,42(3):133-173.

[6] 郭孔辉.汽车操纵动力学[M].长春:吉林科学技术出版社,2012.

[7] 温兴清.基于动态摩擦模型的路面辨识及最优刹车控制研究[D].长沙：中南大学,2008.

[8] 黄铧,左曙光,杨宪武,等.基于LuGre 摩擦模型的轮胎自振系统数值分析[J].计算机辅助工程,2009,18(4):19-23.

[9] 向红标,谭文斌,李醒飞,等.基于LuGre模型的自适应摩擦补偿[J].机械工程学报,2012,48(17):70-74.

[10]殷国栋，金贤建，张云.分布式驱动电动汽车底盘动力学控制研究综述[J].重庆理工大学学报(自然科学)，2016，30(8)：13-20.

(责任编辑 刘 舸)

Research of Dynamic Tire Model Based on LuGre Friction Theory

LI Shengqin, ZHAO Yinbao

(Traffic College,Northeast Forest University, Harbin 150040, China)

Based on the dynamic friction theory, the dynamic tire LuGre model which could be used to study the vehicle dynamic characteristics was set up, and the expressions to describe the vehicle tire longitudinal and lateral forces were established, as a basis for vehicle dynamics simulation. This paper used the genetic algorithm as a tool to identify the model in the static parameters, and then going the parameter identification of dynamic model, and it analyzed the influence of model parameters on the model accuracy. Seven degrees of freedom vehicle dynamics model is set up in the Matlab/Simulink, including the vehicle longitudinal motion, lateral movement and yawing motion and dynamic characteristics of the four wheel rotation. The results show that the accuracy of the established dynamic tire model is good, and it can be used in vehicle dynamic characteristics simulation research.

LuGre friction theory; tire model; vehicle model

2017-02-25

黑龙江省自然科学基金资助项目(E2016003)；中央高校基本科研业务费专项资金资助项目(DL13CB07)

李胜琴(1976—)，女，黑龙江哈尔滨人，博士，副教授，主要从事车辆系统动力学及控制研究，E-mail: lishengqin@126.com。

李胜琴，赵银宝.基于LuGre摩擦理论的动态轮胎模型研究[J].重庆理工大学学报(自然科学)，2017(7):34-39.

format：LI Shengqin, ZHAO Yinbao.Research of Dynamic Tire Model Based on LuGre Friction Theory [J].Journal of Chongqing University of Technology(Natural Science)，2017(7):34-39.

10.3969/j.issn.1674-8425(z).2017.07.005

U467.4

A

1674-8425(2017)07-0034-06