基于PCA和PSO-SVM的手写数字识别应用研究

张校非，白艳萍，郝 岩

(中北大学 理学院， 太原 030051)



基于PCA和PSO-SVM的手写数字识别应用研究

张校非，白艳萍，郝 岩

(中北大学 理学院， 太原 030051)

针对当前手写数字识别正确率较低这一不足，提出了一种主成分分析(PCA)和粒子群算法优化支持向量机(PSO-SVM)的手写数字识别方法。首先，利用PCA降低输入数据的维数，然后把降维的数据作为SVM的输入，用PSO不断优化SVM中的核函数参数g和惩罚因子c，以提高分类精度。实验结果表明：同传统的SVM、GA-SVM、网格搜索算法、卷积神经网络(CNN)相比，PSO-SVM方法分类方法具有最高的识别准确率且运算效率也较高，达98.2%，性能上优于其他几种分类算法。

主成分分析；粒子群算法；支持向量机；手写数字识别

在模式识别的领域中，手写数字识别是其中的一个重要方面。随着计算机和信息技术的日益发展，特别是大数据时代的到来，对手写数字识别的准确度提出了更高的要求。人眼对不同的手写数字识别能力有限，目前对各类数字字体识别，特别是在脱机手写数字识别方面仍处在发展阶段，识别效果仍然不够好[1]。因此，对于手写数字识别的研究具有重大现实意义。

目前，应用于手写数字识别的算法很多,例如有贝叶斯算法[2]、k-means算法[3]、神经网络算法[4-5]、支持向量机(SVM)[6-7]等，其中SVM 分类算法有很好的泛化能力与学习能力[8-10]。SVM 分类算法是以结构风险最小化为目标，所求得的解是全局最优解,该算法克服“维数灾难”问题，使分类算法的效率大大增加，被广泛应用于信号分类、人脸识别、文本分类、垃圾邮件过滤、手写体的识别等领域[11]。

支持向量机在性能优化上还存在很大的问题，为了使其性能达到最优，本文首先用主成分分析(PCA)将手写数字数据进行降维，其次将支持向量机(SVM)与粒子群算法(PSO)相结合，用PSO优化SVM中的相关参数(主要是惩罚参数c和核函数参数g)，避免了欠学习及过学习状态的发生。与传统的SVM、GA-SVM、卷积神经网络(CNN)相比，粒子群算法(PSO-SVM)的识别正确率有显著提高。

1 主成分分析法和PSO-SVM基本原理

1.1 主成分分析(PCA)

主成分分析(principal component analysis，PCA)又称主分量分析，是由皮尔逊(Pearson)于1901年首先引入，后来由霍特林(Hotelling)在1933年进行了发展[1-13]。PCA是一种通过降维方法，把多个变量化为少数几个变量主成分的多元统计方法，这些主成分能够反映原始变量的大部分信息，通常用原始变量的线性组合来表示，为使这些主成分所包含的信息互不重叠，要求各主成分之间相互无关。

主成分分析降维的过程其实就是坐标系旋转变换的过程，新坐标系的各个坐标轴方向是原始数据变差最大的方向，各主成分表达式就是新旧坐标系的转换关系式[14]。

1.2 粒子群算法(PSO)

粒子群优化算法(particle swarm optimization,PSO)最早由Kenney和Eberhart于1995年提出，PSO算法源于对鸟类捕食行为的研究。在鸟类捕食时，每只鸟类找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟类的周围区域[15-17]。

PSO的寻优步骤为：首先随机初始化粒子的位置X和粒子的速度v,然后通过迭代来寻找空间中的最优解。在每次迭代过程中，粒子通过个体极值和全局极值来更新自身的速度和位置，更新公式如下：

(1)

(2)

式中，w为惯性权重；d=1,2,…是种群的维数；i=1,2,…,m是种群的规模；t为当前迭代次数；Vid为粒子的速度；Pid和Pgd分别代表粒子的个体最优值和全局最优值；a1和a2为正的非负常数，称为加速因子；r1和r2为分布在[0,1]之间的随机数。

1.3 PCA和PSO-SVM算法优化步骤

由于手写数字数据集中的每一个数据为一个28×28像素点的图像，一共784维数据，这意味着每个样本有784维数据，这样不但使计算时间增加，而且冗余的信息还会降低分类的精度，所以采用PCA进行降维。

惩罚因子c和核函数参数g对SVM预测精度的影响较大，因此本文将识别正确率当作PSO的适应度函数来不断优化参数c、g，使适应度函数的值达到最大。故提出一种基于粒子群算法的支持向量机优化算法(PSO-SVM)，算法步骤如下：

1) 首先用PCA将手写数字特征进行降维，将降维后的数据作为SVM中的输入；

2) 初始化SVM的惩罚因子c和核函数参数g；

3) 初始化种群的位置和速度，以SVM算法所求得的准确率作为粒子的适应度函数；

4) 用PSO算法对个体粒子进行更新，产生新的粒子并计算其适应度函数值；

5) 判断当前粒子的个体极值是否为种群的全局最优解。若是，则将当前的个体极值替换为全局最优解；若不是，则返回步骤4；

6) 将优化后的参数用于SVM手写数字分类器进行训练，并用手写数字测试集进行测试。

算法主要步骤伪代码如下：

%数据预处理

[Train_data,Test_data,ps]=scaleForSVM(train_data,test_data,0,0.1);

[Train_data,Test_data]=pcaForSVM(Train_data,Test_data,85);

%% 选择最佳的SVM参数c&g

[bestacc,bestc,bestg] = psoSVMcgForClass(train_data_label,data_train);

% 利用最佳的参数进行SVM网络训练

cmd = ['-c ',num2str(bestc),' -g ',num2str(bestg)];

model = svmtrain(train_data_label,data_train,cmd);

%% 子函数 psoSVMcgForClass.m

[bestCVaccuarcy,bestc,bestg,pso_option=psoSVMcgForClass(train_data_label,train,pso_option)

%个体最优更新

if fitness(j) < local_fitness(j)

local_x(j,:) = pop(j,:);

local_fitness(j) = fitness(j);

end

if abs(fitness(j)-local_fitness(j) )<=eps && pop(j,1) < local_x(j,1)

local_x(j,:) = pop(j,:);

local_fitness(j) = fitness(j);

end

%群体最优更新

if fitness(j) < global_fitness

global_x = pop(j,:);

global_fitness = fitness(j);

end

% SVM网络预测

[predict_label,accuracy] = svmpredict(test_label,test_data,model);

2 仿真实验

2.1 PCA降维处理

实验的数据来自于MNIST数据库，共有70 000个样本，从中挑选出60 000个样本作为PSO-SVM训练数据、1 000个样本作为测试数据，有的数字人眼很难区分，部分样本如图1所示。

图1 手写数字样本

首先进行归一化，经过反复实验对比，将样本数据归一化至[0,0.1]区间时，分类效果最好。数据集中每个样本大小均为28×28，即784维数据，这意味着每个样本均有784维数据，这不仅会增加样本的训练时间，也影响到分类器的处理性能。所以，首先要进行PCA降维，除去样本中的冗余信息，同时增加分类器的效率。提取输入数据85%的贡献率，由784维降到59维，降低了92.5%的维数。降维后的前10个特征贡献率如图2所示。

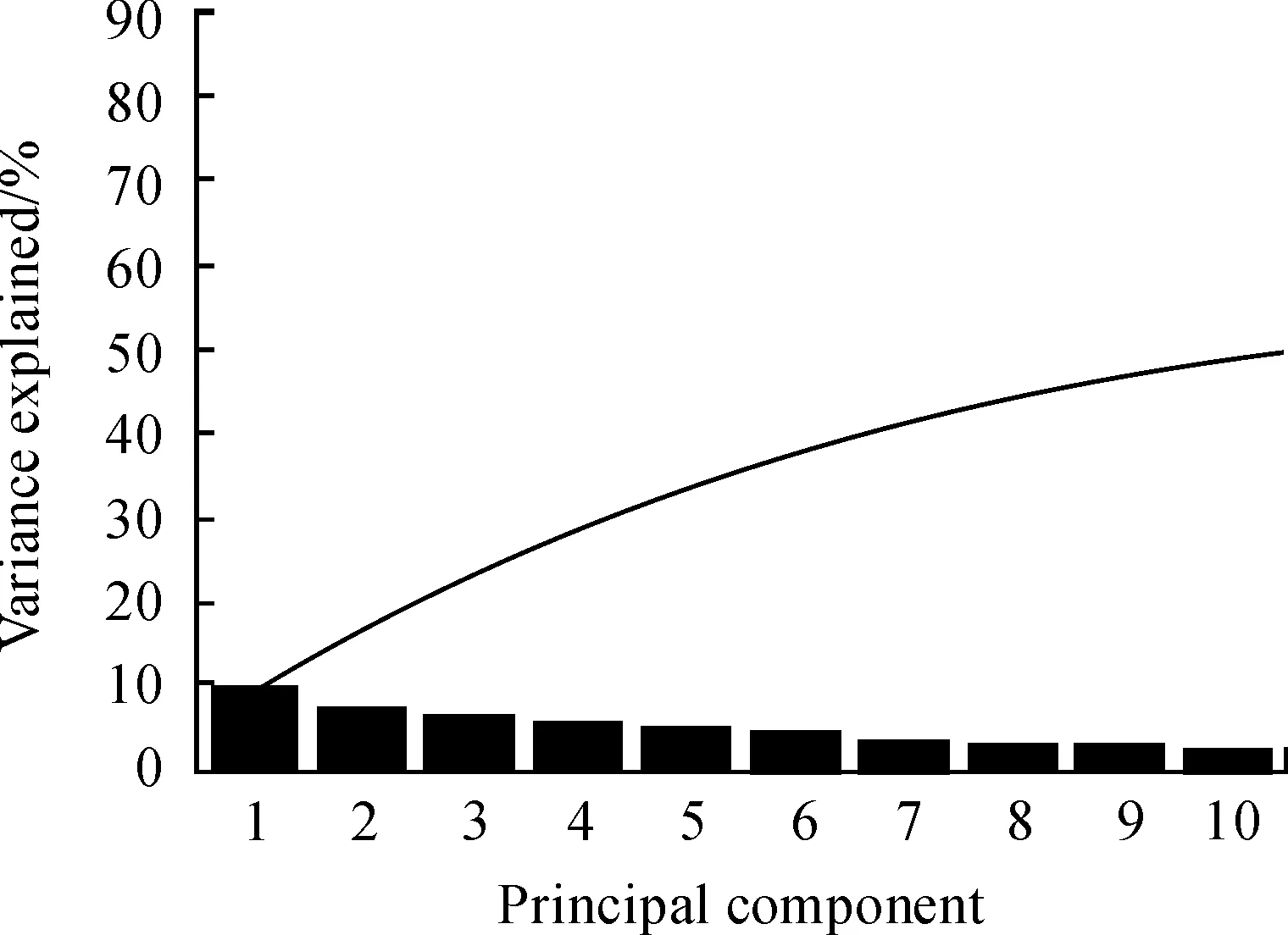
图2 PCA提取出的前10个主成分

从图2中可以看出：前10个特征的累积贡献率达50%以上，与初始的数据维数相比，降低了98.7%，即用1.3%的数据量代表了数据50%以上的特征，这大大降低了数据的复杂度，提高了算法的运算效率。

2.2 PSO-SVM仿真实验

将PCA降维后的数据输入SVM中，利用PSO算法优化SVM，初始种群为20，进化代数为200，c1=1.5，c2=1.7。首先对PSO-SVM进行训练，适应度曲线如图3所示。

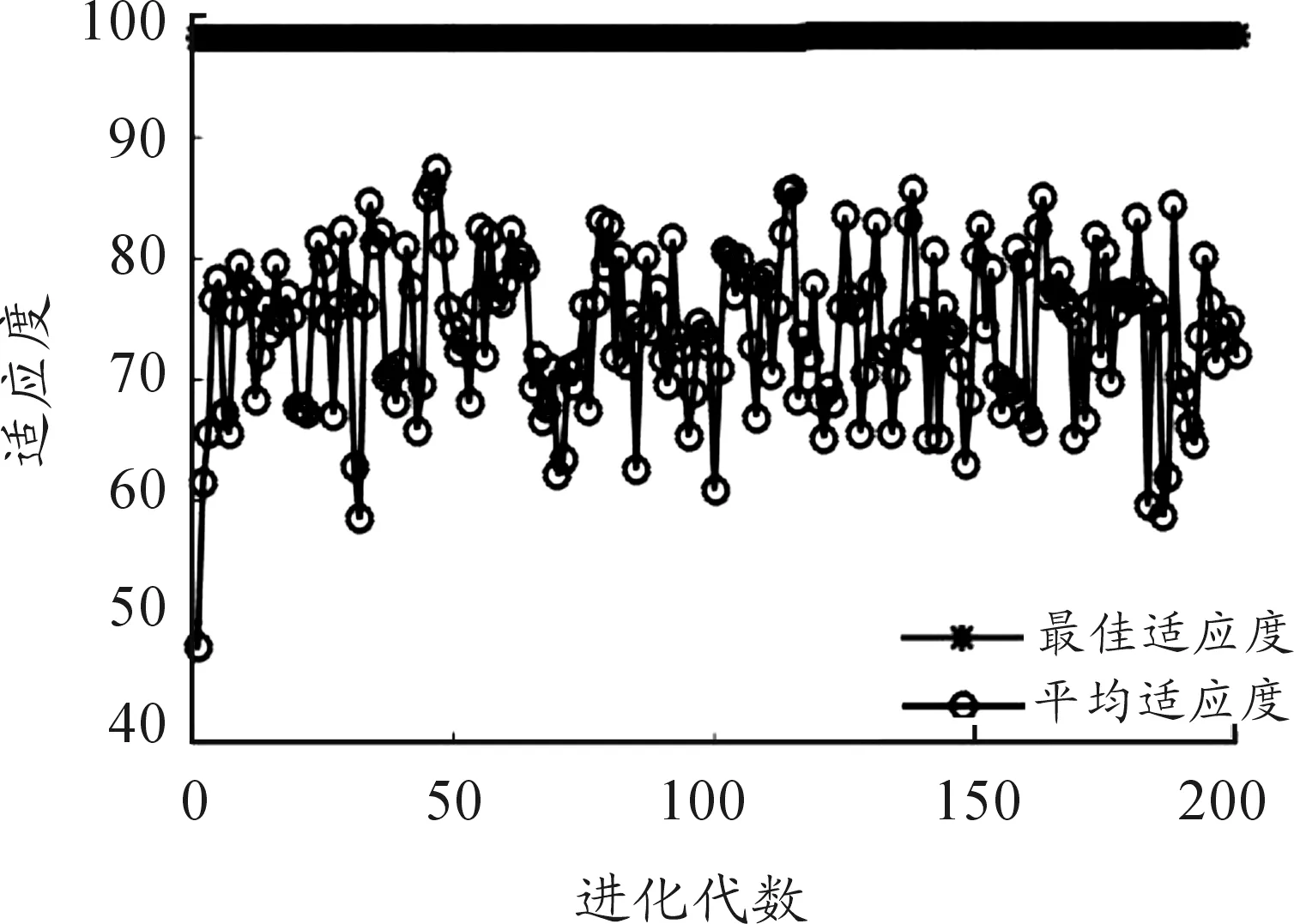
图3 PSO寻找最佳参数的适应度(准确率)曲线

图中x轴代表进化代数，y轴代表训练集的准确率，可以看出：训练过程中粒子的最佳正确率达98.4%，此时惩罚因子c和核函数参数g分别为66.188 8和0.803 34。

下面对测试集进行测试，实验结果如图4所示：

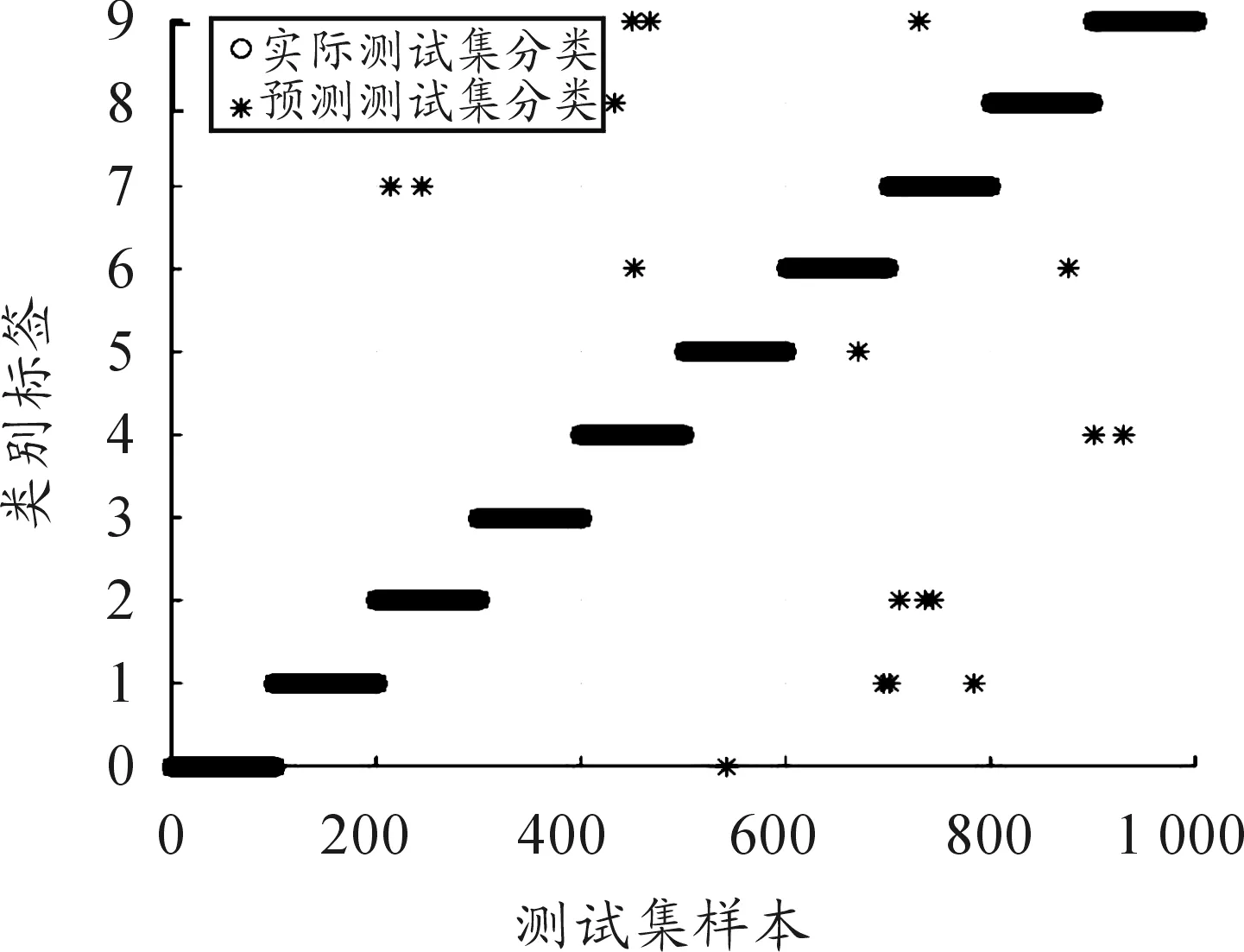
图4 测试结果

通过测试可知：本文所用的方法对手写数字的识别正确率达98.2%，只错分了18个数字，其中对0、1两个数字的识别正确率更是高达100%。又对每种分类器进行50次实验，取50次的平均值：分别与SVM、GA-SVM、网格搜索算法、卷积神经网络(CNN)等几种方法进行了对比，对比结果见表1。

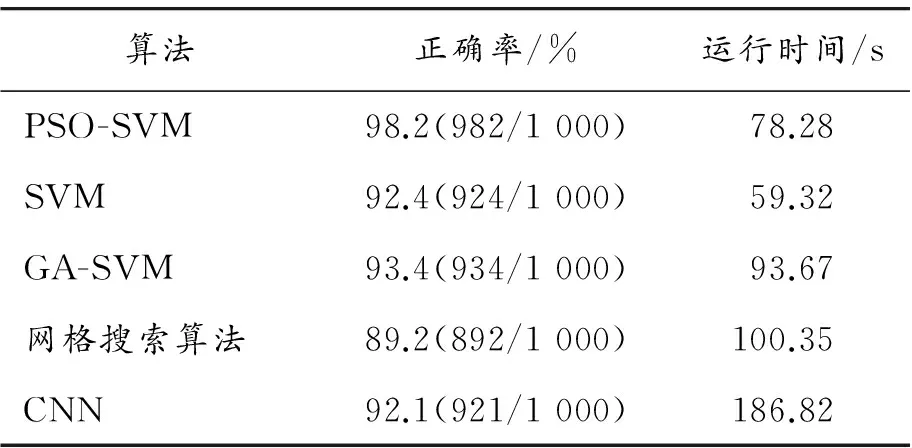
表1 各类算法分类性能对比

从表1中可以看出：PSO-SVM对手写数字数据集在这5种算法中的分类正确率最高，达98.2%。从运行时间上来看，PSO-SVM仅次于SVM，效率高于GA-SVM、网络搜索算法、CNN等3种算法。因此，PSO-SVM算法有更高的精度，且在运算时间上也有很大的优势，具有一定的适用性。

3 结束语

本文首先通过PCA将手写数字集进行降维，其次用PSO算法对SVM中的参数c、g反复训练，不断提升SVM分类器的性能。实验结果表明：PSO-SVM算法对手写数字集的正确识别率有一定的提高，且运算效率较高。同其他几种算法相比，该方法在手写数字识别上有较好的应用前景。

[1] 陈浩翔,蔡建明,刘铿然,等.手写数字深度特征学习与识别[J].计算机技术与发展,2016(7):19-23.

[2] 何岩.统计稀疏学习中的贝叶斯非参数建模方法及应用研究[D].杭州:浙江大学,2012.

[3] 王伟.Kmeans聚类与多波谱阈值相结合的云检测和烟检测算法研究[D].合肥:中国科学技术大学,2011.

[4] 韩力群.人工神经网络教程[M].北京:北京邮电大学出版社,2006.

[5] LÉCUN Y,BOTTOU L,BENGIO Y,et al.Gradient-based learning applied to document recognition[J].Proceedings of the IEEE,1998,86(11):2278-2324.

[6] VAPNIK V.Statistical Learning Theory[M].New York:Wiley,1998.

[7] 牛强,王志晓,陈岱.基于 SVM 的中文网页分类方法的研究[J].计算机工程与应用,2007,28(8):1893-1895.

[8] 吴益红,许钢,江娟娟,等.基于LBP和SVM的工件图像特征识别研究[J].重庆理工大学学报(自然科学),2016,30(1):77-84.

[9] 朱兵,董恩生,郭纲.基于EIS-SVM的飞机复合材料健康监测研究[J].压电与声光,2016(1):115-120.

[10]程思嘉,张昌宏.基于粒子群算法优化最小二乘支持向量机的电路故障诊断方法[J].四川兵工学报,2016,37(3):98-101.

[11]崔健明,刘建明,廖周宇.基于SVM算法的文本分类技术研究[J].计算机仿真,2013,30(2):299-302.

[12]YANG J,ZHANG D,FRANGI A F,et al.Two-dimensional PCA:a new approach to appearance-based face representation and recognition[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2004,26(1):131.

[13]KE Y,SUKTHANKAR R.PCA-SIFT:a more distinctive representation for local image descriptors[J].2004,2(2):506-513.

[14]谢中华.MATlAB统计分析与应用：40个案例分析[M].北京:北京航空航天大学出版社,2015.

[15]SHI Y,EBERHART R C.Empirical study of particle swarm optimization[J].Journal of System Simulation,1999,3(1):31-37.

[16]LIANG J J,QIN A K,SUGANTHAN P N,et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.

[17]李洋,王小川,郁磊,等.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013.

(责任编辑 何杰玲)

Application Research of Handwritten Numeral Recognition Based on PCA and PSO-SVM

ZHANG Xiaofei, BAI Yanping， HAO Yan

(College of Science, North University of China, Taiyuan 030051, China)

In this paper, a new method of handwritten numeral recognition based on principal component analysis (PCA) and particle swarm optimization (PSO-SVM) is proposed for the problem of low accuracy of handwritten digit recognition. Firstly, the dimension of the input data is reduced by PCA, then the dimension reduction data is used as the input of SVM, and the kernel function parametergand the penalty factorcin SVM are optimized by PSO to improve the classification accuracy. The experimental results show that SVM and GA-SVM, with the traditional grid search algorithm, convolutional neural network (CNN) compared with the classification method of PSO-SVM method and it has higher recognition accuracy rate and the operation efficiency is the highest, reached 98.2%, and the performance is better than other types of classification algorithms.

principal component analysis; particle swarm algorithm; support vector machine; handwritten numeral recognition

2016-12-08

国家自然科学基金资助项目(61275120)；山西省回国留学人员科研资助项目(2016-088)

张校非(1991—)，男，硕士研究生，主要从事现代优化算法、神经网络在组合优化中的应用研究，E-mail：598095564@qq.com; 白艳萍(1962—)，女，教授，博士生导师，主要从事神经网络在函数逼近与预测中的应用、神经网络在组合优化中的应用、数据处理与数据融合、非线性动力学的数学建摸与研究，E-mail：974167293@qq.com。

张校非，白艳萍，郝岩.基于PCA和PSO-SVM的手写数字识别应用研究[J].重庆理工大学学报(自然科学)，2017(7):140-144.

format：ZHANG Xiaofei,BAI Yanping，HAO Yan.Application Research of Handwritten Numeral Recognition Based on PCA and PSO-SVM[J].Journal of Chongqing University of Technology(Natural Science)，2017(7):140-144.

10.3969/j.issn.1674-8425(z).2017.07.022

TP39

A

1674-8425(2017)07-0140-05