运用几何直观，发展学生学习力

江苏省苏州市吴江区山湖花园小学 张 斌…

运用几何直观，发展学生学习力

江苏省苏州市吴江区山湖花园小学 张 斌…

几何直观不仅是一种数学思想方法，更是学生数学核心素养的重要组成部分。在数学教学中，运用几何直观，能够发展学生问题的表征力、思维力和创造力。通过几何直观，可以让学生健康用脑、和谐用脑、友善用脑，进而培养学生的数学创造力。

几何直观；数学学习；学习力

几何直观是数学学科中一种极为重要的思想方法，也是学生数学核心素养的重要组成部分。借助几何直观，能够让数学中的复杂问题简单化、抽象问题具体化，进而帮助学生直观、生动地理解数学，形成解决问题的宽畅思路，运用“几何直观”，能够有效地发展学生的数学学习力。

一、运用“几何直观”，发展学生的表征力

数学表征力是学生数学学习的重要学力。对于小学生而言，数学知识无疑是抽象的，因此，将抽象的数学知识直观地表征出来，是学生数学素养形成的一个重要标识。例如，学习认数、学习整数的加减法时，学生常常借助实物、学具或者教具，如小棒、计数器等对数的认识、运算进行直观表征；解决一些数学问题时，学生常常借助画图来表征题意；对于一些行程问题，学生常常展开实地表演或者想象表演等。凡此种种，都是学生数学表征力的体现。教学中，教师要呵护、开发、创新学生表征问题的能力。

例如教学《解决问题的策略——间隔排列》（苏教版小学数学教材第5册）时，面对主题图——“小兔与蘑菇”、“木桩与篱笆”、“夹子与手帕”，有学生用文字叙述，如兔子比蘑菇多一个，蘑菇比兔子少一个；有学生用图形表示，如△比☆多一个，☆比△少一个；还有学生用符号表示，如a比b多一个，b比a少一个等等。对于学生的表征，教师要深度介入，把脉学生的问题，如有学生用图形、符号表征题意时，两端物体并不比中间物体多一个，对此，教师要引导学生展开对比，从两端物体比中间物体多一个，到两端物体和中间物体相等，再到两端物体比中间物体少一个，既要让学生找出它们的区别，也要引导学生洞察它们的联系。只有当学生建立了对应思想后，他们才能真正理解“为什么两端物体相同，两端物体比中间物体多一个”。

正确的数学表征，是解决数学问题的前提和基础。教学中，教师要鼓励学生运用自己的方式呈现自己的思考过程，著名数学家华罗庚说过：“形缺数时难入微，数缺形时少直观。”当学生有意识地、自觉地将抽象的数、规律与具体的形结合起来时，他们就迈上了数学的想象之旅、创造之旅。

二、运用“几何直观”，发展学生思维力

发展学生的思维力，让学生能够借助直观进行推理是几何直观的精髓。在数学教学中，教师要充分运用几何直观，引导学生分析、比较，让学生能够展开直观性的推理。同时，将学生的语言表达与直观图形有机结合起来，实现学生头脑中的表象系统与言语系统的相互转换，促进学生的数学理解，激发学生的数学创造力、

例如教学苏教版《解决问题的策略——相遇问题》（苏教版小学数学教材第8册）的例题——小明家和小芳家分别在学校的西面和东面。小明每分钟走70米，小芳每分钟走60米，他俩同时从家里出发走向学校，经过4分钟两人在校门口相遇，他们两家相距多少米？

笔者在教学中充分运用几何直观，引导学生在纸上画出相应的直观示意图，将复杂的数学问题变得形象，明晰学生解决问题的思路。

1.厘清“问”题，培植作图能力

面对题目中纷繁的信息，学生因事想图。小明每分钟走70米，小芳每分钟走60米，所以学生在用一份表示小明和小芳的速度时，表示小明速度的每份线段要画得长些，表示小芳速度的每份线段要画得短些。他们经过4分钟相遇，说明小明行走了4分钟，小芳也行走了4分钟，因此在画线段图时都应该画这样的4份。

2.看“图”想事，突出思维过程

当学生画图后，笔者引导学生运用“图”叙述题意。“题图结合”，展开分析。小明和小芳同时从家出发，同时相遇，说明他们行驶的时间是相等的。由于小明的速度快些，小芳的速度慢些，所以相同时间内，小明行走的路程应该比小芳行走的路程长些。如此，学生通过图理解了解决问题的难点，把握了问题的实质内涵。

3.依“图”说理，形成解题思路

学生根据自己画的图，形成了两种问题解决方案：一是分别求出小芳和小明的行走路程，然后计算出总路程；二是根据图意，先求出两人每分钟行走多少米，也就是速度和，然后再求出总路程。

学生创图、画图，然后充分发掘图的功能。通过“图导”、“图构”，学生将自己的思维过程清楚地表达出来，并努力理解他人的思考方式。直观、形象化的图形，助推学生突破思维的瓶颈，进而有效地解决问题。

三、运用“几何直观”，发展学生的创造力

发展学生的想象力、推理力等是几何直观教学的核心。在数学教学中，教师要引导学生依图联想，培养学生的创新意识和实践能力。小学生思维的特质是形象思维占据主导地位，并逐步向抽象思维过渡。在教学中，教师要引导学生善于将抽象的问题形象化，将内隐的思维外显化、可视化。

例如教学《解决问题的策略——画图》（苏教版小学数学教材第8册）时，学生遇到了这样的一道题：育才小学有一块周长为50米的长方形试验田。如果长和宽各增加5米，这块试验田的面积增加了多少平方米？学生依据题意将图画好后，其创造性思维令人惊讶。（如右图）

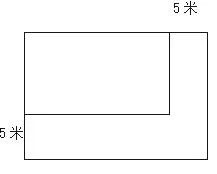
在交流展示中，有学生采用假设法：假设原来长方形的长是20米，宽是5米，原来的面积是100平方米，现在的面积是250平方米，现在的面积比原来的面积增加了150平方米。有学生采用分割法：将增加的面积分成三部分。第一部分的面积是“宽×5”；第二部分的面积是“5×5”；第三部分的面积是“长×5”。将第一部分和第三部分合并，也就是宽×5+长×5，即“周长的一半×5”。所以用50÷2×5=125（平方米），125+25=150（平方米）。还有学生采用重叠法：首先将现在长方形的周长求出是50+20=70（米），然后将增加的部分分割成两个互相重叠的部分：第一部分用宽×5；第二部分用长×5；再减去重叠部分的面积。列式就是（长+宽）×5-25，也就是35×5-25=150（平方米）。

著名数学教育家张广厚先生说，“数学无疑是一门高度抽象的学科，需要人们具有高度抽象思维的能力，但同时也需要很强的几何直观能力。”在数学教学中，发展学生几何直观，能够开发学生的左右脑，让学生的抽象性、概括性的逻辑思维与直观、顿悟式的直觉思维紧密相连。如此，才能开掘学生的大脑潜能，让学生健康用脑、和谐用脑、友善用脑，进而激发学生的数学创造性。