对考查向量的试题背景分析与教学备考建议
2017-08-09上海市第四中学
上海市第四中学 …周 科
对考查向量的试题背景分析与教学备考建议
上海市第四中学 …周 科
《上海市高中数学学科教学基本要求》(试验本)以及《普通高等学校招生全国统一考试上海卷考试手册》都强调对学生创新意识和创新能力的考查,考查的目的是基于强调培养中学生的个性品质,开拓中学生的数学视野,促进中学生理性思维的逐步形成。多年来,上海的高考试卷命制过程中都希望所命制的试卷能很好地贴切这一考查要求,通过命题专家的努力,这些年的数学高考卷都出现了很多具有创新性的试题。但这些好题也恰恰是学生难以逾越的一道道坎,这一方面暴露出当前数学教学中知识迁移、组合、融汇的程度不高,能力区域不宽泛,创新意识不强,同时,学生也没能很好地发挥数学基本思想、基本方法在这类题中的基础性、工具性作用。本文仅就向量及其应用中的问题,通过几个典型例题做一个探究。
一、向量题的考查特点分析及典型例题剖析
1.以向量为背景,考查三角函数
依据《上海市中小学数学课程标准(试行稿)》及其调整意见和高考选拔人才的选拔要求,结合中学教学实际,考试旨在考查学生的数学素养。如何在三角函数、向量这些传统意义下的中低档试题中进行能力立意呢?近几年的上海卷给出了较为满意的回答。譬如:
例1 (2016年高考数学上海卷理科第12题)在平面直角坐标系中,已知上的一个动点,则的取值范围是。
试题分析:本题利用数形结合思想,将问题转化到单位圆中,从而转化成平面向量的坐标运算,利用三角函数的图象和性质,得到的取值范围。主要考查了考生的逻辑推理能力、基本运算求解能力、数形结合思想、转化与化归思想等。
2.以向量为背景,考查函数的值域
高考命题以基础知识为载体,结合对基本思想、基本方法与技能的考查,突出考查学生分析问题、转化问题、解决问题的能力,在解题思路和方法的寻找上突显学生的数学素养。近几年高考数学上海卷在这一点上做得比较成功。譬如:
例2 (2012年高考数学上海卷理科12题) 在平行四边形ABCD中,边AB、CD的长分别为2、1,若M、N分别是边BC、 CD上的点,且满足的取值范围是。

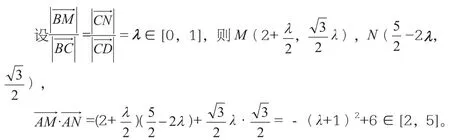
解法1是用向量的数量积运算,将其转化为函数问题;解法2是采用“建系”,用平面向量运算的坐标表示转化为函数问题。本题较好地考查了学生用数学基本知识和技能解决数学问题的能力。
3.以向量为背景,考查概率
高考命题要遵循《考试说明》,在高考数学《考试说明》中提出试题具备高信度、效度、必要的区分度和适当的难度。传统涉及概率的试题一直是单一知识点,将向量和概率相结合,较为充分地践行了这一宗旨。
例3 (2016年高考数学上海卷理科第14题) 如图,在平面直角坐标系xOy中,O为正八边形的中心,,任取不同的两点点P满足则点P落在第一象限的概率是
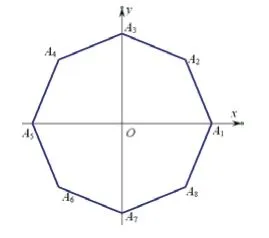
试题分析:本题主要考查古典概型概率的计算。解答本题的关键在于能准确确定所研究对象的基本事件空间、基本事件个数,利用概率的计算公式求解。本题能较好地考查考生的数学应用意识、基本运算求解能力、数形结合思想等。
4.……以向量为背景,考查解析几何中存在性问题
例4 (2014年高考数学上海卷理科第14题) 已知曲线若对于点存在C上的点P和 L上的点Q使得的取值范围为。

本题考查了两个基本能力:推理论证和运算求解。运算能力是思维能力和运算技能的结合,提高运算求解能力的关键是“算理”,要让思在算之前,通过思明确算的方向,并对运算结果有一定的预见性。
5.以向量为背景,考查多变量问题
现在已进入大数据的信息化时代,高考试题也顺应这一变化,命题时除了设置一些“三基”试题外,也设置了一些信息量大、多变量的问题。譬如:

本题信息量大,综合性强,思维要求高,考查学生对信息的提取和处理能力,考查学生运算求解能力和分析、解决问题的能力。
二、备考建议
1.注重基础,加强知识交汇性训练
结合近几年上海卷对向量知识点的考查特点,在向量复习中要注重对基础知识的内在挖掘,考查知识的交汇性问题比较多,因而在课堂教学中,我们要注重基础知识,加强能力培养,从注重学习结果向注重学习过程转变,要从学会转向会学,要让学生从被动接受转向主动发现,要从信息单向传递转向信息多向交流,以适应课程改革的新要求。
2.重视数学思想方法的应用,培养学生运算能力
解决数学问题是离不开数学思想方法的,数学思想方法在解决问题中有着举足轻重的地位,方法选择得当,往往有出奇制胜的效果,方法思路混乱,可能导致思维受阻。另外,要加强学生运算能力的培养,有不少学生就是因为运算能力不强导致计算错误,进而影响解题的进度,使得解答陷入困境。
3.解题思路的生成才是教学的重点
高三主要是解题教学,解题教学就是教会学生学会如何解题、怎样解题,而不是只给学生讲题、把题讲明白、把题讲懂。高三教学中教学时间紧、任务重,总感觉时间不够用,课堂上师生都有些囫囵吞枣——基础教学不够扎实,例题、习题的讲解更是急于求成,教师往往不注重“解题思路的生成过程”的分析、传授、讲解,而过多地关注或停留在答案和解题上。著名教育学家波利亚的解题理论告诉我们:解题要做到“七分构思(读题、审题、发散、联想、归纳),三分表述(书写、运算、订正、反思与回顾)”;解题无外乎就是“架起由已知通向未知的桥梁,桥梁承载着数学知识、思想、方法、能力、技巧”。教学中教师必须清楚“我讲明白,不等于学生明白,更不等于学生理解、掌握和熟练运用”,加强解题教学的过程分析、注重解题思路与脉络生成的传授是教会学生的关键。
4.适当加大向量的研究难度,突出其工具性
从近几年的高考试题来看,有关向量的考查难度呈不断增大的趋势。向量是代数和几何的桥梁,向量既可作为表达问题的工具,也可作为解决问题的工具,本文例3中的向量兼备两者的功能。
5.加强对上海卷考试大纲和考试说明的研究
高考命题的指导思想之一,是突出对数学基础知识、基本技能、基本思想方法的考查。《考试说明》中对知识的考查要求依次分为三个层级:记忆水平;解释性理解水平;探究性理解水平。考试要求对向量的考查要求为:(1)解释性理解平面向量分解定理,会求向量的长度及夹角,懂得运用向量方法进行简单的几何证明;(2)探究性理解向量的数量积运算及其性质,平面向量的坐标表示,会用坐标讨论两个向量的平行或垂直。在复习过程中要依据学科基本要求和考试说明,仔细推敲、认真研究、全面铺开,不放过任何一个可能考查到的知识点,注重在知识交汇处设置问题,培养学生处理综合问题的能力。
6.注重回归课本,加强对往年试题的研究
课本是教学之本,在最后的复习过程中,一定要加强对课本习题、重点例题的探究,注重对教材的挖掘和利用,许多好的高考试题都源于教材而高于教材,是对教材的二次开发和再利用,因此一定要用好教材,加强对课本的研究。
[1]2017年《普通高等学校招生全国统一考试上海卷考试手册》
[2]过家福,王华民.三角函数、向量试题特点及应对策略[J].中学数学教学与参考,2017(5).
[3]胡书军,李素香,霍红梅.解题思路的生成才是解题教学的重中之重[J].中学数学教学与参考,2016(5).
