设而不求在解题中的灵活应用
2017-08-08福建
福建 林 静
设而不求在解题中的灵活应用
福建 林 静
“设而不求”是数学解题中一种灵活并能简化计算的解题方法,通过把存在但难求的某个量假设出来,利用代换来规避正面强求的计算,应用恰当可以起到事半功倍的作用.
1.设而不求在函数与导数中的应用



【例2】(2016·新课标Ⅰ卷理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(Ⅰ)求a的取值范围;
(Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2<2.【解析】(Ⅰ)由f(x)=(x-2)ex+a(x-1)2=0
当x<1时,g′(x)<0,g(x)为减函数,x→+1,g(x)→-∞;x→-∞,g(x)→0;
当x>1时,g′(x)>0,g(x)为增函数,x→+1,g(x)→-∞;x→∞,g(x)→+∞.
由条件得-a<0即a>0.则a的取值范围为(0,+∞).
(Ⅱ)法一:由(Ⅰ)可知当a>0时直线y=-a与y=g(x)有两个交点且g(x1)=g(x2).
由条件不妨设x1<1,x2>1,则2-x1>1,则g(x2)=g(x1)<g(2-x1),而y=g(x)在x>1上为单调递增函数,x2<2-x1,则x1+x2<2.
法二:由条件不妨设x1<1,x2>1,则2-x1>1,
则f(x2)=f(x1)=(x1-2)ex1+a(x1-1)2=0,
则f(2-x1)=-x1e2-x1+a(x1-1)2.
设h(x)=-xe2-x-(x-2)ex,
则h′(x)=(x-1)(e2-x-ex)<0,h(x)>h(1)=0.
即f(2-x1)>0=f(x2).
由a>0,可判断f(x)在x>1上单调递增,2-x1>x2,
即x1+x2<2.
【评析】法一根据直线y=-a与y=g(x)有两个交点,假设交点(x1,g(x1)),(x2,g(x2))利用对称性、函数增长速度以及函数的单调性找出g(x1)与g(2-x1)的大小关系.避免了求交点的坐标;法二是假设方程的解并用解表示参数建立函数,利用单调性寻找关系2-x1>x2,避免了解方程.
2.设而不求在解三角形中的应用
通过假设未知数建立方程,借用未知数利用设而不求解决三角形中的有关问题.
【例3】(2011·新课标卷Ⅰ理·16)在△ABC中,∠B= 60°,则AB+2BC的最大值为_______.
【解析】条件中只有一边和一角,因此要设置未知数,建立方程,构建函数.
【例4】在△ABC中,角A、B、C所对应的边分别为a、b、 c,c=2,点D在AC上.

(Ⅰ)当BD⊥AB,且BD=2时,求BC的长;
(Ⅱ)当AD=2DC且BD=1时,求△ABC的面积S△ABC.
【解析】(Ⅰ)由正弦定理易求.

即9x2=a2+2a+4①,∵∠ADB+∠BDC=π,
化简得:6x2=2a2+1②,
【评析】通过假设线段DC的长x建立方程①②,通过替换x解决了问题规避了烦琐的计算.
3.设而不求在直线与圆锥曲线相交位置关系问题中的应用
(1)设而不求在求直线与圆锥曲线相交得到的弦长中的应用
通过韦达定理利用避免了求直线与圆锥曲线的交点坐标.
【例5】(2016·新课标Ⅰ卷理·20)设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C、D两点,过B作AC的平行线交AD于点E.
(Ⅰ)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(Ⅱ)设点E的轨迹为曲线C1,直线l交C1于MN两点,过B且与l垂直的直线与圆A交于PQ两点,求四边形MPNQ面积的取值范围.

法二:由条件可设M(x1,y1),N(x2,y2),
若m≠0,直线l的方程为x=my+1,
即mx+y-m=0.
所以四边形MPNQ面积为

若m=0,直线l的方程为x=1,
易求|MN|=3,|PQ|=8,四边形MPNQ面积为12.综上,四边形MPNQ面积的取值范围为.
法三:由条件可设M(x1,y1),N(x2,y2),若k∈R,k≠0,直线l的方程为y=k(x-1),
即x+ky-1=0.
则.
若k∈,直线l的方程为x=1,
易求|MN|=3,|PQ|=8,四边形MPNQ面积为12.
【评析】通过假设直线l交曲线C1的交点MN的坐标,利用韦达定理巧妙地避免正面求交点坐标的复杂计算.
(2)设而不求在求动点的轨迹方程中的应用
利用设而不求建立所求点的坐标与主动点的坐标之间的关系,再通过主动点所在的曲线建立所求点的轨迹方程.
【例6】已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.
(Ⅰ)求线段AP中点的轨迹方程;
(Ⅱ)若∠PBQ=90°,求线段PQ中点的轨迹方程.
【解析】(Ⅰ)线段AP中点的轨迹方程为(x-1)2+y2=1,过程略;
(Ⅱ)设线段PQ中点坐标为(x,y),点P(x1,y1),Q(x2,y2).则x1+x2=2x,y1+y2=2y.
即(x1-1)(x2-1)+(y1-1)(y2-1)=0
x1x2+y1y2-2x-2y+2=0,由(x1+x2)2+(y1+y2)2=4x2+4y2得x2+y2-x-y=1.
线段PQ中点的轨迹方程为x2+y2-x-y=1.
(3)设而不求在证明定值中的应用
通过假设点的坐标利用它所满足的曲线方程而解决问题.
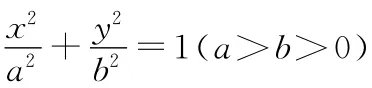
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P的椭圆C上一点直线PA与y轴交于点M,直线PB与N轴交于点N.

4.设而不求在有关向量问题中的应用
【例8】已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么的最小值为 ( )

【解析】通过假设未知数,利用未知数建立所求问题的函数解析式,使用设而不求解决问题.
设∠APO=α(0°<α<90°),
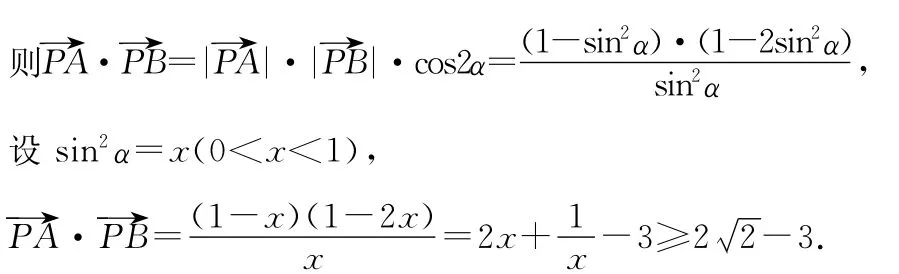
通过以上例题可以看到,设而不求在数学解题中是一种灵活且能突破计算瓶颈的方法.
(作者单位:福建省武平第一中学)
