立体几何中的球类模型问题

长春 林逸凡

立体几何中的球类模型问题

长春 林逸凡

球与多面体的内接外切问题是立体几何中一类常见的特殊题型，球类问题有着自身独特的解题方法和数学思想．近年来，在各地的高考题与模拟题中，球类模型问题频频出现，越来越受到命题者的青睐．本文展示了球类模型问题的几种常见题型，并归纳解决相应问题的常见解题思路与技巧．

一、截面法

【例1】半径为4的球的两条弦AB、CD的长度分别等于，M、N分别为AB、CD的中点，每条弦的两端都在球面上运动，有下列四个命题：①弦AB、CD可能相交于点M；②弦AB、CD可能相交于点N；③MN的最大值为5；④MN的最小值为1．其中真命题的个数为 （ ）

A．1个 B．2个 C．3个 D．4个

【解析】当弦AB、CD相交时，则在一个截面圆上，由于AB＜CD，所以弦AB、CD可能相交于点M，弦AB、CD不可能相交于点N．故①是真命题；②是假命题；连接OM、ON，当OMN为三角形时，由于OM＋ON＞MN，OMON＜MN，所以，当MN共线且在球心O的不同侧时，MN取得最大值5；当MN共线且在球心O的同侧时，MN取得最小值1．故③④为真命题．

【点评】解决球类模型的截面问题时，通常策略是“化立体为平面”，确定截面所确定的圆面的半径，将“截面与球”的问题转化为“大圆与弦”的问题．

球心到截面的距离d与球半径R及截面圆的半径r有下面关系：．

【变式】已知过球面上三点A、B、C的截面和球心的距离等于球半径的一半，且AB＝BC＝CA＝1，则该球的半径是 （ ）

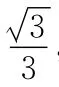
【例2】在半径为R的球内做内接圆柱，则内接圆柱全面积的最大值是 （ ）

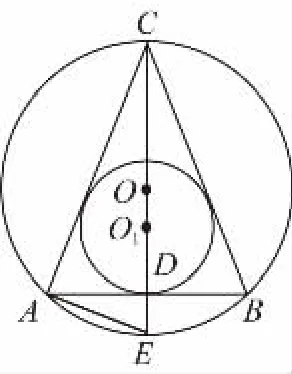
【变式】一个高为16的圆锥内接于一个体积为972π的球，在圆锥内又有一个内切球．

求：（Ⅰ）圆锥的侧面积；

（Ⅱ）圆锥的内切球的体积．

【解析】（Ⅰ）如图所示，作轴截面，则等腰三角形CAB内接于⊙O，⊙O1内切于△CAB，

二、体积桥

【例3】设棱锥M－ABCD的底面是正方形，且MA＝MD，MA⊥AB，如果△AMD的面积为1，试求能够放入这个棱锥的最大球的半径．

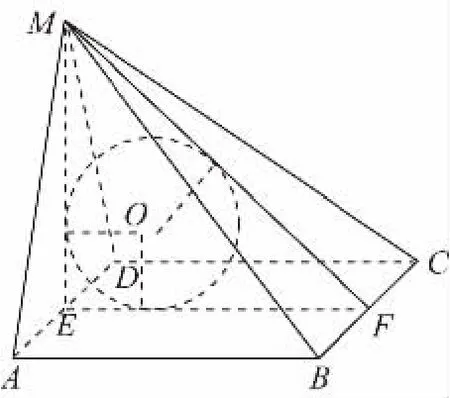
【解析】因为AB⊥AD，AB⊥AM，

所以AB⊥平面MAD．

所以平面MAD⊥平面ABCD，

设E是AD的中点，从而ME⊥AD．

所以ME⊥平面ABCD，ME⊥EF，

能够放入这个棱锥的最大球为与平面MAD、平面ABCD、平面MBC相切的球，

不妨设O∈平面MEF，

于是O是△MEF的内心．设球O的半径为r，

【变式】正四面体的棱长为3，则它的外接球的表面积等于 （ ）

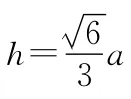
三、射影法

【例4】一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为36π，那么这个正三棱柱的体积是 （ ）

【解析】球半径为R＝3，正三棱柱的高即为2R＝6，将正三棱柱拦腰横切一刀，球的截面为一个大圆，正三棱柱的截面为正三角形，大圆是正三角形的内切圆，故正三角形的边长为，从而得正三棱柱的体积是．

【点评】射影法，作球心到其中一个面的射影，则相应的线段应与面垂直，而球心与顶点连线即为外接球半径，设出未知数，列方程求解．正棱柱是上下底面都是正多边形的直棱柱，故外接球心在底面的射影应为正多边形的中心，对于多边形的边为偶数条的情况，如正四棱柱、正六棱柱，由对称性，外接球心即为上下底面相对四个顶点连出的矩形的对角线长的一半；对于多边形的边为奇数条的情况，如正三棱柱、正五棱柱，可连接外接球心与底面中心，该线段长即为棱柱高的一半，再连接球心与一个顶点，该长度即为外接球的半径，利用勾股定理列方程求解．

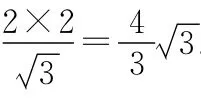
【变式2】一个正六棱柱的各个顶点都在一个球的表面上，这个六棱柱的侧棱长是它的底面的边长a的2倍，则该球的半径为_______．

【解析】由对称性，外接球心即为上下底面相对四个顶点连出的矩形的对角线长的一半，底外接圆的直径为2a，侧棱长2a，故该球的半径是边长为2a的正方形的对角线长的一半，即．

四、补形法

【例5】直三棱柱ABC－A1B1C1的各顶点都在同一球面上，若AB＝AC＝AA1＝2，∠BAC＝120°，则此球的表面积等于_______．

【解析】因为AB＝AC，∠BAC＝120°，A，B，C可看作一个正六边形的三个顶点，故可将这个直三棱柱ABCA1B1C1补形，装回到一个正六棱柱中，二者的外接球是一样的，转化为求正六棱柱的外接球半径．由对称性，外接球心即为上下底面相对四个顶点连出的矩形的对角线长的一半，底外接圆的直径为4，侧棱长2，故矩形的对角线长为，外接球半径为，表面积等于20π．

【点评】补形法，将多面体嵌入到形状更对称、且具有相同的外接球的长方体、正棱柱中去，再转用第四种策略求解．

【变式】若三棱锥的三条侧棱两两垂直，且侧棱长均为，则其外接球的表面积是_______．

【解析】法一（补形法）：装回到边长为的立方体中，易得立方体体对角线为3，从而外接球的半径，从而表面积是9π．

五、以点代球

【例6】三个半径为1的球，两两相切放置于水平桌面上，在三球中间上方再放上一个半径为2的球，则其最高点距离桌面的距离为 （ ）

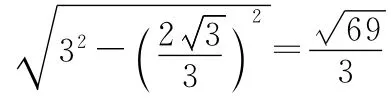
【点评】“擒贼先擒王”，解球抓球心，先抓住球心之间的位置关系，再转为球与球、球与面之间的关系．球与球外切时，球心之间的线段的长度为两球的半径之和，当多个球相切时，则球心的连线可构成多面体．

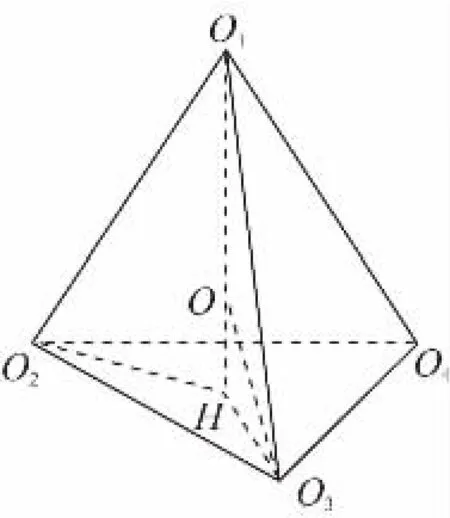
【变式】半径为R的球内部装有4个半径为r的小球，则小球半径r的最大值是 （ ）

【解析】将4个小球的球心连接起来够成一个正四面体，

O1在底面O2O3O4上的射影设为H，则大球的球心O显然在O1H上，如图所示．

（作者单位：吉林省长春市吉大附中实验学校）