绝对值不等式的求解策略

河北 陈星萌

绝对值不等式的求解策略

河北 陈星萌

解绝对值不等式是高考的热点和重点，而解含绝对值的不等式的关键是去掉绝对值的符号，其基本思想是把含绝对值的不等式转为不含绝对值的不等式．

解含有绝对值不等式时，去掉绝对值符号的方法主要有：公式法、分段讨论法、平方法、几何法等．这几种方法应用时各有利弊，在解只含有一个绝对值的不等式时，用公式法较为简便；但是若不等式含有多个绝对值时，则应采用分段讨论法；应用平方法时，要注意只有在不等式两边均为正的情况下才能运用．

一般的，含绝对值不等式的常用解法主要有如下几种方法，我们分别讨论．

一、基本性质法

二、几何意义法

根据绝对值的几何意义，｜x｜是指数轴上点x到原点的距离；｜x1－x2｜是指数轴上x1、x2两点间的距离；而｜xa｜＋｜x－b｜的几何意义则是在数轴上设与实数x、a、b对应的点分别为P、A、B，上式的几何意义为｜PA｜＋｜PB｜．因此，我们完全能够利用绝对值的几何意义简便求解以下类型的不等式：｜ax＋b｜≤c；｜ax＋b｜≥c；｜x－a｜＋｜x－b｜≥c；｜x－a｜＋｜x－b｜≤c．

【例2】解下列不等式：

（1）｜x－1｜＋｜x＋2｜≥5；

（2）｜x＋1｜＋｜x－1｜≥3．

【解析】（1）｜x－1｜＋｜x＋2｜≥5的几何意义是数轴上的点到1与－2的距离之和大于等于5的实数，所以不等式的解为x≤－3或x≥2，即不等式的解集为（－∞，－3］∪［2，＋∞）．

（2）如下图，设数轴上与－1、1对应的点分别为A、B，那么A、B两点的距离和为2，因此区间［－1，1］上的数都不是不等式的解．

设在A点左侧有一点A1到A、B两点的距离和为3，A1对应数轴上的x．

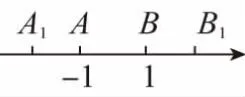
同理设B点右侧有一点B1到A，B两点距离和为3，B1对应数轴上的x，

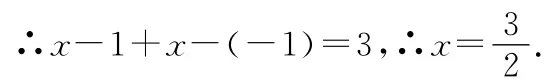
从数轴上可看到，点A1、B1之间的点到A，B的距离之和都小于3；点A1的左边或点B1的右边的任何点到A、B的距离之和都大于3．

三、定义法（或叫零点分区间法）

含有两个或两个以上绝对值符号的不等式，可用零点分区间法脱去绝对值符号，将其转化为与之等价的不含绝对值符号的不等式（组）求解．

用零点分段法解绝对值不等式的步骤：①求零点；②划区间，去掉绝对值符号；③分别解去掉绝对值的不等式；④取每个结果的并集，注意在分段时不要遗漏区间的端点值．

【例3】解不等式：｜x－2｜＋x｜x＋2｜＞2．

【解析】当x≤－2时，不等式化为（2－x）＋x（－x－2）＞2，解得－3＜x≤－2；

当－2＜x＜2时，不等式化为（2－x）＋x（x＋2）＞2，解得－2＜x＜－1或0＜x＜2；

当x≥2时，不等式化为（x－2）＋x（x＋2）＞2，解得x≥2；

所以原不等式的解集为｛x｜－3＜x＜－1或x＞0｝．

四、平方法

利用两边平方也可以去掉绝对值符号，这适应于两边都是正数的绝对值不等式．对于形如｜ax＋b｜≥｜cx＋d｜的不等式，可以利用两边平方的形式转化为二次不等式求解．

【例4】解下列不等式：

（1）｜2x－1｜＞｜2x－3｜；

（2）x2－｜x｜－2＜0．

【解析】（1）本题也可采取前面的方法：采取用零点分区间讨论去掉绝对值，但是比较复杂．如果利用两边平方，即根据｜a｜＞｜b｜a2＞b2解之，则更显得流畅简洁．原不等式同解于（2x－1）2＞（2x－3）2，即4x2－4x＋1＞4x2－12x＋9，即8x＞8，得x＞1．所以原不等式的解集为｛x｜x＞1｝．

（2）不等式原不等式可化为｜x｜2－｜x｜－2＜0，解得－1＜｜x｜＜2．∵｜x｜≥0，∴0≤｜x｜＜2，∴－2＜x＜2．

∴原不等式的解集为｛x｜－2＜x＜2｝．

【变式】解不等式｜x－2｜＜｜x＋1｜．

五、数形结合法

对于｜x－a｜＋｜x－b｜≥c（c＞0）和｜x－a｜＋｜x－b｜≤c（c＞0）形式的不等式，可以直接去掉绝对值，转化成分段函数，画出分段函数的图象，也可以作出不等式两边所对应的两个函数和y1＝｜x－a｜＋｜x－b｜和y2＝c的图象，然后结合图象图象求解．

【例5】解不等式｜2x－1｜＋｜x－3｜≤4．

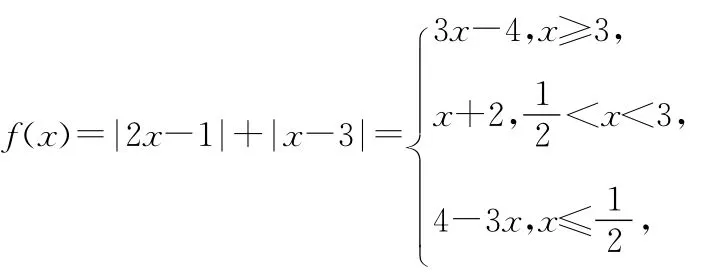
其图象如图所示，与直线y＝4相交于点A（0，4）和B（2，4），∴该不等式的解集为｛x｜0≤x≤2｝．

【变式】已知函数f（x）＝｜x＋1｜－｜2x－3｜，求不等式｜f（x）｜＞1的解集．

【答案】f（x）＝｜x＋1｜－｜2x－3｜

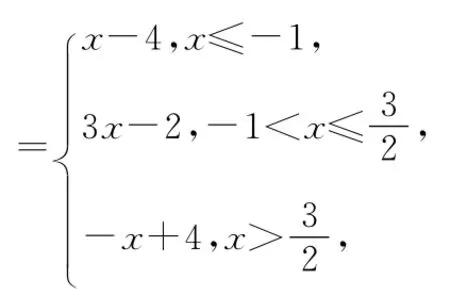
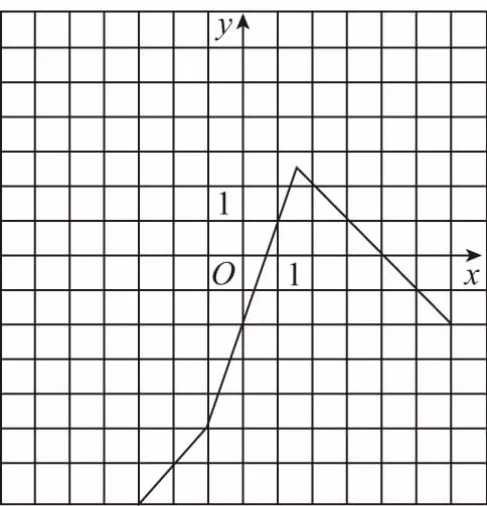
故y＝f（x）的图象如图所示．

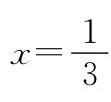
六、含参数的绝对值不等式

的取值范围是_______．

【解析】通过讨论x的范围结合二次函数的性质得到Δ≥0，求出a的范围即可．

若存在x∈R使g（x）≥f（x），

即x2＋｜x－a｜＋a－4≤0有解，

x≥a时，x2＋x－4≤0，显然有解，

x＜a时，x2－x＋2a－4≤0，

解含有参数的绝对值不等式时，除按绝对值不等式来解外，还必须对参数进行分类讨论，在讨论时，要注意“不重不漏”的原则．同时，解含有参数的绝对值不等式时，常常由于忽略了对参数的正负讨论而出现错误，应该注意避免．

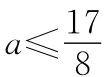
形如｜f（x）｜＞g（x）的不等式可借助｜ax＋b｜＞c的解法，转化为f（x）＜－g（x）或f（x）＞g（x）（g（x）＞0），当然｜f（x）｜＜g（x）－g（x）＜f（x）＜g（x）．如果f（x）的正负能确定的话，也可以直接去掉绝对值符号．

【例7】设a＞0，b＞0，解关于x的不等式：｜ax－2｜≥bx．

【解析】原不等式可化为ax－2≥bx或ax－2≤－bx，即

【答案】原不等式可化为｜x－1｜＜｜x＋a｜．

两边平方得x2－2x＋1＜x2＋2ax＋a2，

即2（a＋1）x＞1－a2，当a＋1＞0，即a＞－1时，

当a＋1＝0，即a＝－1时，∴此时原不等式无解．

当a＋1＜0，即a＜－1时，

纵观近年各地高考数学试题，在对不等式的考查中，绝对值不等式的解法是高考的热点和重点问题，可谓每年必考、每卷必考，题目难度一般为中、低档，着重考查利用数形结合的能力以及化归与转化思想．高考对这部分要求不是太高，高考中有选择题和填空的形式，而新课标等则以选做题的形式考查．可以预计2017年高考绝对值不等式仍将是考试的重点，应引起我们的高度重视．

（作者单位：河北省衡水市第一中学）