全国高考圆锥曲线命题规律研究

江苏 韩文美 陆维香

全国高考圆锥曲线命题规律研究

江苏 韩文美 陆维香

一、全国高考圆锥曲线部分试题特点及命题规律

1．从地位上看：圆锥曲线在高考中一直占据重要的地位，理科总体稳定，文科分值有变小的趋势（转化为直线与圆内容），稳中求新，难度较前几年有变小的趋势．

2．从方向上看：考题遵循《考试大纲》和《考试说明》，立足基础，贴近教材，突出能力考查．

3．从题型上看：选择题、解答题为主，也出现个别填空题，一般题量维持在“一大二小”，有时文科会有其中的一题变为直线与圆内容，分值维持在17～22分左右．

4．从考频上看：结合近六年新课标高考Ⅰ中的文理卷，考查椭圆知识出现12次，考查双曲线知识出现10次，考查抛物线知识出现13次，这三个知识的考查次数基本相当；而在解答题中，以考查椭圆与抛物线为主，其中考查椭圆知识出现4次，考查抛物线知识出现5次．

5．从难度上看：以中档题和难题为主，选择题一般位于4～5题与9～10题的位置，填空题一般位于14～16题的位置，大题一般位于解答题第五题的位置．

6．从考点上看：重点考查椭圆、双曲线、抛物线的定义、标准方程与几何性质，直线与圆锥曲线的位置关系，轨迹方程的求解，圆锥曲线与平面向量、导数、不等式等的交汇与综合问题等．

二、全国高考圆锥曲线部分重点、热点、难点、冷点分析

1．圆锥曲线的定义问题

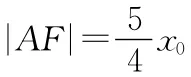
A．1 B．2 C．4 D．8

【分析】结合定义把抛物线上的点到焦点的距离转化为抛物线上的点到准线的距离，通过该点的横坐标与p的关系建立方程，即可求解对应的参数值．

【点评】圆锥曲线的定义一直是新课标高考的一大热点问题，几乎每两年的高考题就会出现一次，是一个高频考点．其命题规律是：（1）直接根据定义求解对应的圆锥曲线方程或轨迹方程；（2）根据定义结合圆锥曲线方程转化确定对应线段长度的和或差、参数值等，能达到化难为易、化繁为简、事半功倍的效果．

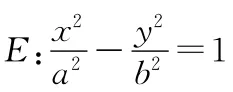
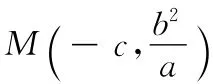
2．圆锥曲线的方程问题

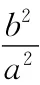
【解析】设A（x1，y1），B（x2，y2），则x1＋x2＝2，y1＋y2＝－2，

把点A、B代入方程后两式相减，

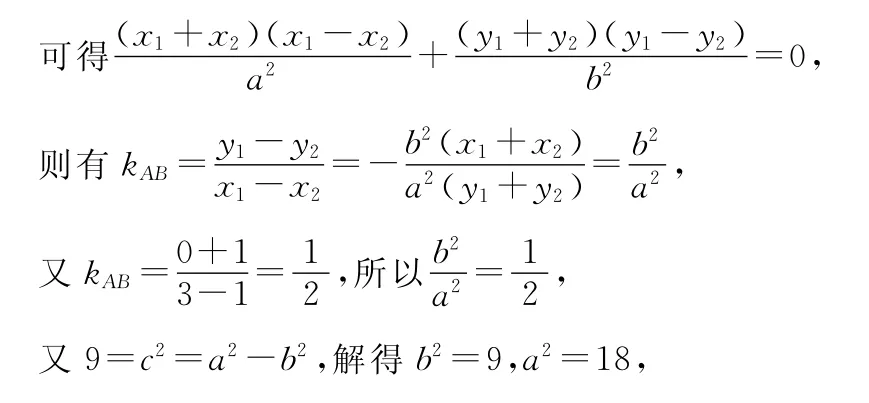
【点评】圆锥曲线的方程一直是高考的重点问题，凡是涉及圆锥曲线的问题几乎都与对应的方程有关，这是一个回避不了的高频考点．其命题规律是：根据圆锥曲线的定义确定方程，结合圆锥曲线的性质确定方程，结合解析几何中曲线的位置关系确定方程等．同时，圆锥曲线的方程的求解有时单独设置问题，有时通过圆锥曲线的方程的求解来达到解决相关几何性质的目的，有时圆锥曲线的方程的求解只是问题解决的一部分，这些都是高考中比较常见的命题方式．

【变式2】（2015·新课标Ⅱ文·15）已知双曲线过点（4，，且渐近线方程为，则该双曲线的标准方程为________．

3．圆锥曲线的几何性质问题

【分析】设出相应的顶点与焦点，利用题目条件建立关系式，并利用等积法思维来转化与应用，进而确定参数a与c的关系式，从而得以求解椭圆的离心率．

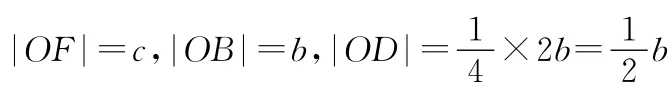
【点评】圆锥曲线的几何性质是新课标高考的一大热点问题，有时也是问题设置的难点所在．圆锥曲线的几何性质沟通定义、方程、直线与圆锥曲线的位置关系等问题，是圆锥曲线中不可或缺的一大考点．其命题规律是：求解圆锥曲线的离心率、相应点（顶点或焦点）的坐标、双曲线的渐近线、抛物线的准线，有时还涉及不同圆锥曲线之间的比较与关系，相应点与线之间的位置关系与距离问题等，都是高考中比较常见的命题类型．

【变式3】（2014·新课标Ⅰ理·4）已知F为双曲线C：x2－my2＝3m（m＞0）的一个焦点，则点F到C的一条渐近线的距离为 （ ）

【解析】可得渐近线方程为及c＝，则对应距离为．

【点评】本题的结果可作为一条双曲线的性质记下来，即“双曲线的焦点到渐近线的距离等于b”．

4．直线与圆锥曲线的位置关系问题

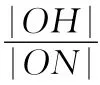
【分析】（1）求出直线ON的方程，与抛物线方程联立，求出H点的坐标，即可求出相应的比值；（2）求出直线MH的方程，与抛物线方程联立求解，即可判断直线MH与C的交点个数．

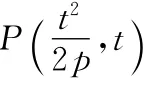
（2）直线MH与C除H以外没有其他公共点．理由如下：

【点评】直线与圆锥曲线的位置关系一直是高考中解答题部分回避不了的考点，有时小题中也经常出现，是高考的一大热点与难点问题，几乎每年高考均有涉及．其命题规律是：通过直线与圆锥曲线的位置关系的建立，解决中点弦问题、弦长问题、位置关系问题等，常常以综合题的形式出现，一般为中档题和难题．往往通过数形结合建立相应的关系式或通过代数形式转化为二元二次方程组的解的问题进行讨论来解决．

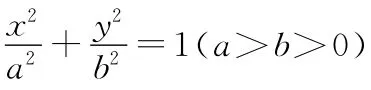
（1）求E的方程；

（2）设过A的动直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程．

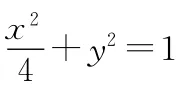
5．圆锥曲线中的轨迹问题

【典例5】（2016·新课标Ⅰ理·20）设圆x2＋y2＋2x－15＝0的圆心为A，直线l过点B（1，0）且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E．证明｜EA｜＋｜EB｜为定值，并写出点E的轨迹方程．（节选）

【分析】通过平行线的性质，结合圆的相关性质，通过三角形中等角对等边的转化确定定值问题，并利用椭圆的定义来求解相应的轨迹方程．

【解析】因为｜AD｜＝｜AC｜，EB∥AC，

故∠EBD＝∠ACD＝∠ADC，所以｜EB｜＝｜ED｜，

故｜EA｜＋｜EB｜＝｜EA｜＋｜ED｜＝｜AD｜，

又圆A的标准方程为（x＋1）2＋y2＝16，

从而｜AD｜＝4，

所以｜EA｜＋｜EB｜＝4，

由题设得A（－1，0），B（1，0），｜AB｜＝2，

【点评】轨迹问题经常作为高考解答题中的一部分出现在新课标高考的试题中，是高考的一个热点问题，关键是抓住条件，结合对应的方法加以求解，为进一步研究圆锥曲线的相关问题打下基础．这是近年来新课标高考中轨迹问题的命题规律，难度不大，只是作为综合题的切入点出现．

【变式5】（2016·新课标Ⅲ·20）已知抛物线C：y2＝2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点．若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程．

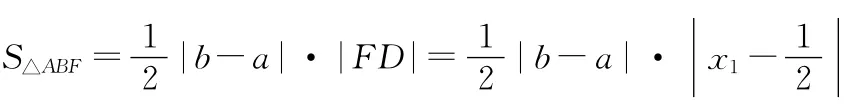
6．圆锥曲线中的最值问题

【分析】要求△APF的周长的最小值，其实就是转化为求解三角形三边长之和，根据已知条件与双曲线定义加以转化为已知边的长度问题与已知量的等价条件来分析，根据直线与双曲线的位置关系，通过数形结合确定点P的位置，通过求解点P的坐标进而利用三角形的面积公式来处理．

【解析】设双曲线的左焦点为F1，根据双曲线的定义可知｜PF｜＝2a＋｜PF1｜，则△APF的周长为｜PA｜＋｜PF｜＋｜AF｜＝｜PA｜＋2a＋｜PF1｜＋｜AF｜，

由于｜AF｜＋2a是定值，要使△APF的周长最小，则｜PA｜＋｜PF1｜最小，即P、A、F1共线，

【点评】圆锥曲线中的最值问题是高考题中的常考问题之一，也是高考中的一大难点，往往难度比较大，知识交汇性强．新课标高考中最值问题的命题规律是：参数的最值问题、几何图形的面积的最值问题等，而距离的最值问题等会是新课标高考的一大冷点．此类问题创新性强、思维拓展、难度较大．

（1）求M的方程；

（2）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．

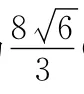
7．圆锥曲线中的定值问题

（1）求C的方程；

（2）直线l不过原点O且不平行于坐标轴，l与C有两个交点A、B，线段AB中点为M．证明：直线OM的斜率与直线l的斜率的乘积为定值．

【分析】（1）根据椭圆的离心率公式、已知椭圆上的点以及关系式a2＝b2＋c2可求得椭圆的方程；（2）设出直线l的方程，通过联立方程，确定线段AB的中点M 的坐标，利用斜率公式求解对应的斜率，即可得以证明两相关直线的斜率的乘积为定值．

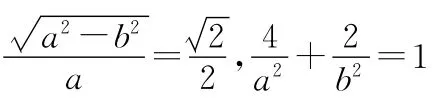
解得a2＝8，b2＝4，

（2）设直线l：y＝kx＋b（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），

得（2k2＋1）x2＋4kbx＋2b2－8＝0，

所以直线OM的斜率与直线l的斜率的乘积为定值．

【点评】圆锥曲线中的定值问题是新课标高考命题的一个热点，也是圆锥曲线问题中的一个难点．新课标高考中定值问题的命题规律是：关系式乘积的定值、比值的定值、参数关系式的定值、数量积的定值、直线过定点等问题，有时作为小题出现，有时是综合题中的较难部分．往往依题设条件直接推导出定值或由特殊情形找到定值，然后进行一般性推理论证．

【变式7】（2015·新课标Ⅱ理·20）已知椭圆C：9x2＋y2＝m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值．（节选）

8．圆锥曲线中的探究问题

【典例8】（2015·新课标Ⅰ理·20）在直角坐标系xOy中，曲线与直线l：y＝kx＋a（a＞0）交与M，N两点．

（1）当k＝0时，分别求C在点M和N处的切线方程；

（2）y轴上是否存在点P，使得当k变动时，总有∠OPM＝∠OPN？说明理由．

【分析】（1）求出M，N的坐标，利用导数求出C在点M和N 处的切线方程；（2）作出判定，利用设而不求思想将y＝kx＋a代入曲线C的方程整理成关于x的一元二次方程，设出M，N的坐标和P点坐标，利用设而不求思想，将直线PM，PN的斜率之和用a表示出来，利用直线PM，PN的斜率之和为0，即可求出a，b的关系，从而找出适合条件的P点坐标．

【解析】（1）由题设可得，或

（2）存在符合题意的点，证明如下：

设P（0，b）为符合题意的点，M（x1，y1），N（x2，y2），直线PM、PN的斜率分别为k1、k2，将y＝kx＋a代入C的方程整理得x2－4kx－4a＝0，故x1＋x2＝4k，x1x2＝－4a，

当b＝－a时，有k1＋k2＝0，则直线PM的倾斜角与直线PN的倾斜角互补，

故∠OPM＝∠OPN，所以P（0，－a）符合题意．

【点评】圆锥曲线的探究问题一直是新课标高考试卷中的热点与难点问题之一，也是2017年新课标高考的冷点问题，要引起高度重视．圆锥曲线的探究问题命题规律主要是：包括探索条件型与探索存在型两主要大类，其试题立意新颖，形式多样，体现了“开放探索，考查探究精神，开拓展现创新意识的空间”的高考命题指导思想与命题原则，已成为高考试题的一个新亮点，也是新课程理念下的一道亮丽的风景线．

【变式8】（2015·新课标Ⅱ理·20）已知椭圆C：9x2＋y2＝m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．若l过点，延长线段OM与C交于点P，四边形OAPB能否为平行四边形？若能，求此时l的斜率，若不能，说明理由．

（节选）

【解析】当l的斜率为时，四边形OAPB能为平行四边形．（过程略）

（作者单位：江苏省张家港职业教育中心校）