在阅卷中思考提升
——从一道中考题学生解题过程中折射出的教学问题
2017-08-07朱叶青
朱叶青
(浙江省杭州市萧山区北干初级中学,浙江 杭州 311200)
在阅卷中思考提升
——从一道中考题学生解题过程中折射出的教学问题
朱叶青
(浙江省杭州市萧山区北干初级中学,浙江 杭州 311200)
教师在平时教学中要重视课本,高于课本,用好教材,用活教材.注重学生的解题过程,善于从学生的解题过程中发现存在的问题.笔者就浙江省2014年某市初中数学卷中一道试题进行阅卷后的思考.
中考;阅卷;教学;思考
纵观近年来各地的中考试题,不难发现考查内容依据“《全日制义务教育数学课程标准》以下简称《标准》”回归课本,体现基础性.很多题目都可以在课本中找到原型,对纠正一些教师抛开数学课本进行题海训练的做法有一定作用.2016年本人有幸参加中考初中数学网上阅卷,其中第23题不管是学生还是老师第一眼见到它绝对会很高兴,因为“众里寻他千百度,她却在课本练习处.”追根寻源,此题源于教材《浙教版数学八年级上册》第86页16题.此题就学生的解题过程中发现值得深思的教学问题.

等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.
(1)若AE=CF,①求证:AF=BE,并求∠APB的度数.②若AE=2,试求AP·AF的值.
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
【典型情形一】此题空白或得0分的学生有5000多名,占参加中考总人数的百分之十几.
此题的第(1)①源于教材,教材中的原题是:
如图①,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.
【原因分析一】笔者分析认为此题空白或得0分的绝大部分同学是因为学习态度不端正,缺乏责任感所造成,这部分同学可以说在学校基本已经放弃学习.因为第(1)①源于教材《浙教版数学八年级上册》第86页第16题,并且比教材中还要更简单,因为多了“AF=BE”的证明,学生更容易想到通过全等进行解决问题.而全等三角形的证明应该说是初中几何图形这部分内容中最基本的推理,对于学生来说也是最得心应手的推理.再说求∠APB的度数,即使你从推理的角度得出,只要学生有想多得1分欲望,很容易猜到答案的120°,或者用量角器量出∠APB的度数也可得1分.
【教学思考一】重视课本,高于课本,用好教材,用活教材
纵观这几年的中考数学试题,我们发现,相当数量的题是书本上的例题、习题的间接引用、巧作改编而成的,综合题也是集基础知识的组合、加工及发展,体现出关注教材之基础功能.这类试题往往具有典型性,源于、高于、活于教材.因此,在教学中,要排除各种资料的干扰,充分发挥教材的作用,对典型的例、习题重视挖掘其蕴含的深层潜力,认真探索一题多解,一题多变,一题多用、一题多思等.
【典型情形二】第(1)②不会做或方法不好的同学占20%左右.

【原因分析二】第(1)②不会做的学生可以看出对基本图形不够熟悉,这题是《相似三角形》主题中典型的“A”型.而思考方法不好的学生则是因缺乏数学整体思想意识,要求AP·AF的值,在学生脑里就想到先分别求出AP和AF,所以导致思考方法不合理.
【教学思考二】要把对数学思想方法的领悟放在首位
数学思想方法是数学中的精髓,是联系数学中各类知识的纽带,最常见的数学思想有:函数与方程、转化与化归、分类讨论、数形结合等.总之,无论是听讲、阅读,还是进行复习、作业,都要认真领悟这些思想方法,学会运用这些思想方法.这样,不仅能学得知识,还能认识知识缘起和发展的过程、以及解题思路探索的过程、解题方法和规律抽象概括的过程,从而培养优秀的思维方法,促进自身数学能力的发展.

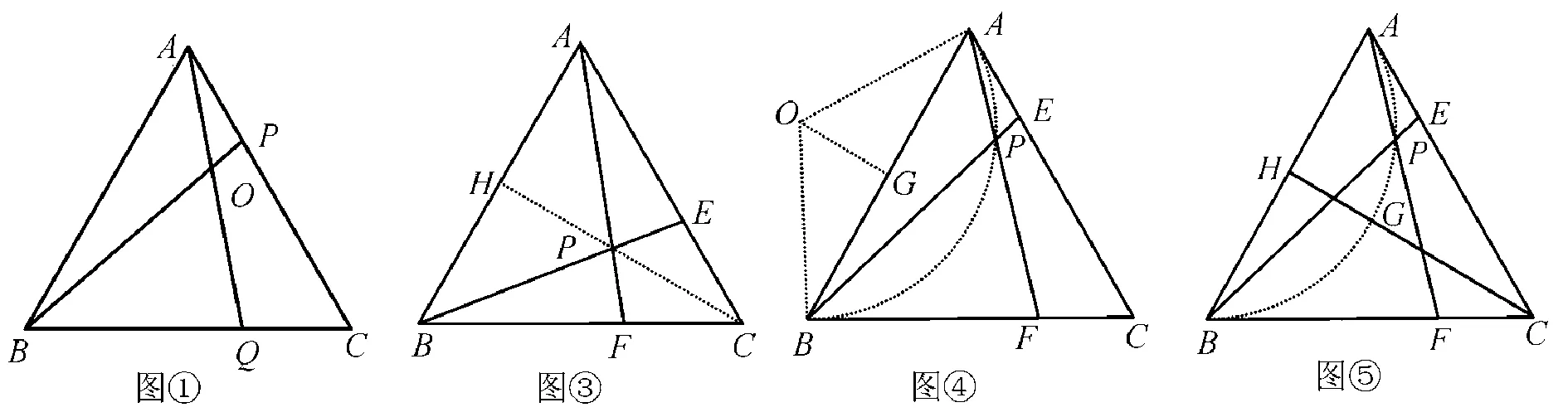
【原因分析三】很多学生一看到这种动点轨迹问题就被吓倒了,根本就不敢去尝试解决问题.个人认为主要是由于平时教师在课堂上留给学生思考、动手、探究的时间太少了,遇到这样较新的问题很多学生根本就无从下手.
【教学思考三A】注重探究过程,培养探究的习惯与能力
要促进学生能力的发展,教师要关注引导学生关注自主学习体验的过程,重视知识的呈现过程.数学概念、定理、法则等知识的推理逻辑过程,需要经历观察、分析、综合、归纳、类比、猜想及证明过程.就本题而言探究动点所经过的路径长,在九年级最后的复习阶段学生肯定会有所接触,但为什么只有15%左右的学生敢去尝试呢?就是因为学生从来就没有真的掌握解题的方法.比如九年级在最后一轮专题复习中,不要急于赶进度,必须一个专题一个专题好好落实,敢于花时间、留空间让学生动手活动、观察、分析、尝试、讨论.比如轨迹问题一定要让学生动笔画,学生必须要有充分的实践空间,在自主探索、实践、合作交流等活动中解除困惑,在合作交流、与人分享和独立思考的氛围中,学会倾听、质疑、说服、推广而直至豁然开朗.
【教学思考三B】学会质疑,开启走向探究之路的大门
教师需引导学生积极主动地去学、去思、去问,鼓励学生多问、深问、怪问.特别是对有“独到见解”或“异想天开”“别出心裁”的学生应更多关注,跟踪动态.教师在赏识、鼓励学生质疑的同时,还要培养学生学会质疑的能力.鼓励学生去质疑、批判、否定,敢于和课本挑刺,敢于与老师挑战;同时对于自己的解题过程能做到“回头望”,能认真反思结果的合理性等,养成日思严谨的思维习惯.对于第(2)小题要善于观察条件的细微变化,如:(1)为什么把AE=CF变为(2)AF=BE?这样对题目有什么影响?要求点P经过的路径长,需先知道什么?我得通过什么方法得到路径的轨迹?等等.多问自己几个为什么?从而把问题解决.
【教学思考三C】突破思维定势,培养学生思维的灵活性
介于以上的思考,笔者认为:在教学中,教师应该把课堂的时间和空间尽可能多的还给学生;在课后,对不同的学生给予不同的指导,对不同的学生提出不同的要求;在改作业时,不能简单的批改对与错,更应注重学生的解题过程,从中发现问题,以便及时改之;在平时,不断给自己充电,争取走在新课改的前沿;在完成教学工作之余,多思考、多反思、勤动笔,做个研究型的教师.
[1]刘兼,孙晓天.全日制义务教育数学课程标准(实验稿)[M].北京:北京师范大学出版社,2002.
[2]顾继玲,章飞主.初中数学新课程教学法[M].北京:开明出版社,2003:4-5.
[3]张丽晨.初中数学课堂教学艺术[M].北京:中国林业出版社,2004:299-303.
[4]郭味纯.教师怎样进行写反思与写案例和论文[M].北京:中国林业出版社,2000:7-20.
[责任编辑:李克柏]
2017-05-01
朱叶青(1983-),女,浙江杭州人,本科,中学二级教师,从事中学数学教育.
G632
B
1008-0333(2017)17-0007-02
