过阻尼搓板势系统的随机共振∗
2017-08-07谢勇刘若男
谢勇刘若男
1)(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,西安 710049)
2)(西安交通大学数学与统计学院,西安 710049)
过阻尼搓板势系统的随机共振∗
谢勇1)†刘若男2)
1)(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室,西安 710049)
2)(西安交通大学数学与统计学院,西安 710049)
(2017年2月10日收到;2017年3月21日收到修改稿)
研究在周期信号和高斯白噪声共同作用下过阻尼搓板势系统的随机共振.由于用直接模拟法研究随机系统所用时间较多,考虑用半解析的方法对系统的随机共振现象进行研究.在弱周期信号极限下,结合线性响应理论和扰动展开法提出一种计算系统线性响应的矩方法.在此基础上,利用Floquet理论和非扰动展开法将矩方法扩展到系统非线性响应的计算.通过直接数值模拟结果和矩方法所得结果的比较展示了矩方法的有效性并采用均方差作为量化指标给出其适用的参数范围.研究结果表明,以系统的功率谱放大因子作为量化指标,发现在适当的参数条件下,系统的共振曲线有一个单峰出现,说明过阻尼搓板势系统存在随机共振现象.而且在一定范围内调节偏置参数时,共振曲线的峰值随偏置参数的增大而增大;在调节驱动幅值时,随机共振效应随驱动幅值的增大而增强.
随机共振,线性响应理论,Floquet理论,矩方法
1 引 言
随机共振本质上是一种噪声增强信噪比的统计现象,是Benzi等[1]在解释地球冰川时代周期性发生现象时所提出的概念.目前随机共振现象已广为人知[2,3],并跨越学科边界存在于多个学科领域,如细胞生物学[4]、化学反应[5]、经济金融[6]、信号探测[7,8]、社会系统[9]等.
布朗粒子在周期势系统中的运动是一个非常重要的理论抽象模型,比如超离子导体的导电性[10]、约瑟夫森结[11]、分子生物马达[12]等.因此,周期势系统中的随机共振现象不论是在过阻尼[13−17]还是欠阻尼[18−22]情形下都引起了广泛的研究兴趣.Kim和Sung[13]利用数值方法对周期势系统中的随机共振进行了研究,通过跃迁模型说明了过阻尼周期势系统中不存在随机共振现象.Dan等[14]研究了非均匀介质中质点在过阻尼搓板势系统中的运动,发现当选取质点的迁移率作为量化指标时,系统会出现随机共振的现象.Tu等[15]对非均匀介质中非对称耦合粒子在周期势场中的运动建立了分数阶模型,采用分数阶差分法进行数值仿真研究其定向输运现象,发现当系统存在噪声时,粒子链平均速度出现了广义随机共振现象.Fronzoni和Mannella[16]通过搭建锁相环电路进行直接模拟发现了倾斜的周期势系统中的随机共振现象,但在尝试用基于线性响应理论的方法研究随机共振时,其理论推导和模拟结果的符合程度并不令人满意.Marchesoni[17]考察了白噪声激励下过阻尼搓板势系统的随机共振现象,研究表明在线性响应意义下,当满足绝热近似条件时,随机共振会发生在临界偏置附近.我们考虑用半解析的矩方法研究周期信号和高斯白噪声共同作用的过阻尼搓板势系统的随机共振.本文以一个单位质量的质点在搓板势系统中的过阻尼运动为研究对象,其势函数表达式为满足以下Langevin方程:

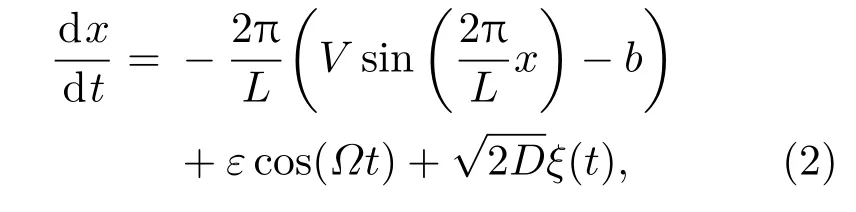
其中V=V0/γ,b=b0/γ,ε=ε0/γ,D=/γ.
当周期信号非常弱时,即0<ε≪1,此时系统(2)对应的确定性系统近似地等价为

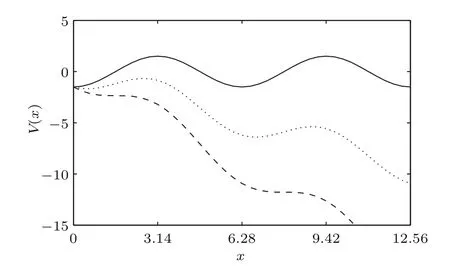
图1 系统势函数V(x) (参数V=1.5,L=2π;b=0(实线),b=0.5V(点线),b=V(短划线))Fig.1.The potential function.The curves correspond to b=0(solid line),b=0.5V(dotted line),and b=V(dashed line),respectively,when V=1.5 and L=2π.
本文首先应用线性响应理论对受弱周期信号激励的过阻尼搓板势系统进行研究,提出基于扰动展开法的矩方法,通过比较矩方法和直接数值模拟法所得结果验证矩方法的有效性,并通过计算系统功率谱放大因子研究随机共振现象.然后,根据Floquet理论,给出基于非扰动展开法的矩方法,并对其适用范围加以研究.
2 基于扰动展开法的矩方法
以P(x,t)表示系统(2)在时刻t的状态概率密度,则它的Fokker-Planck(FP)方程为
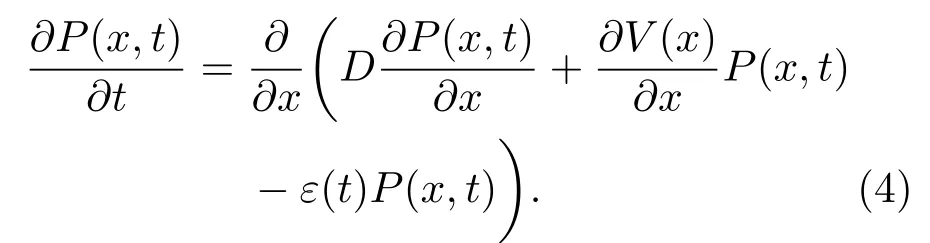
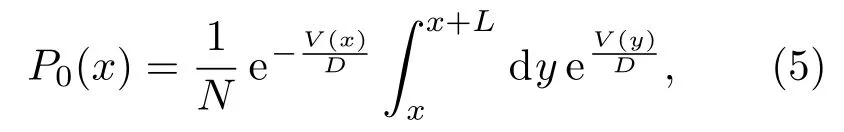
假设ε≪1,在线性响应意义下,方程(4)的解可以分解为[25]
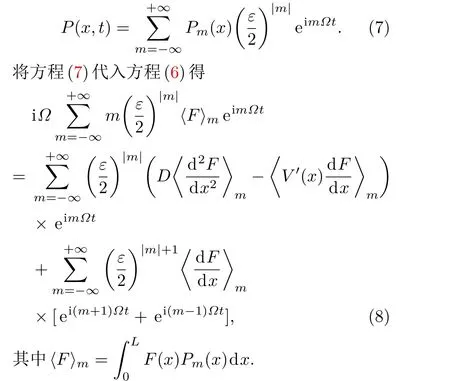
利用三角函数系的正交性并舍去ε的高次项得
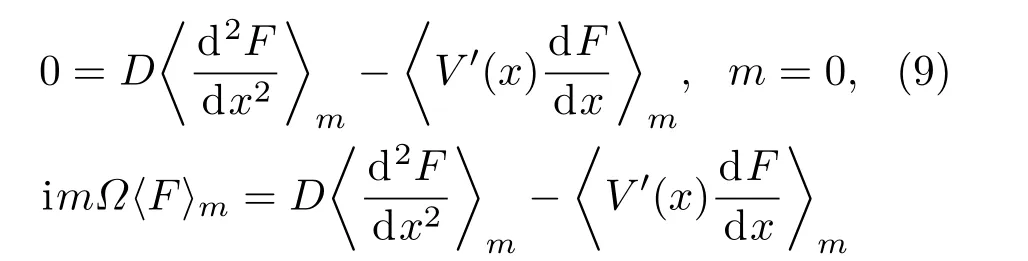
由概率规范化性质可知,P(x,t)必须满足约束条件
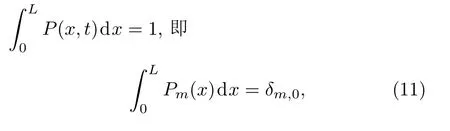
其中δm,0为Kronecker符号.
考虑到pm(x)是周期为L的函数,把它展成如下形式的三角级数[26]:
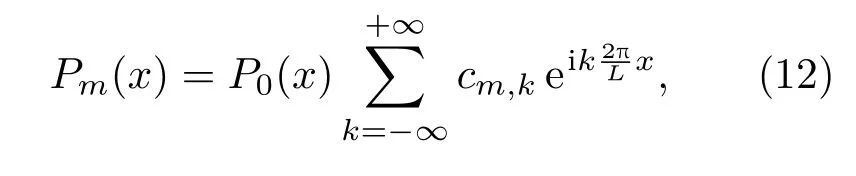
其中c0,k=δ0,k,并且选取
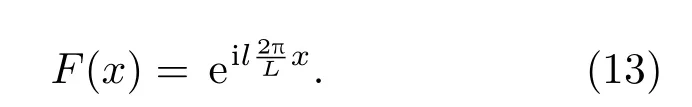
将展(12),(13)式代入方程(10),有

这里〈·〉0表示对未扰随机系统的平稳分布(3)取期望,也称作未扰随机系统的平稳矩.
当l=0即F(x)=1时,有

这和概率规范化性质(11)式一致.
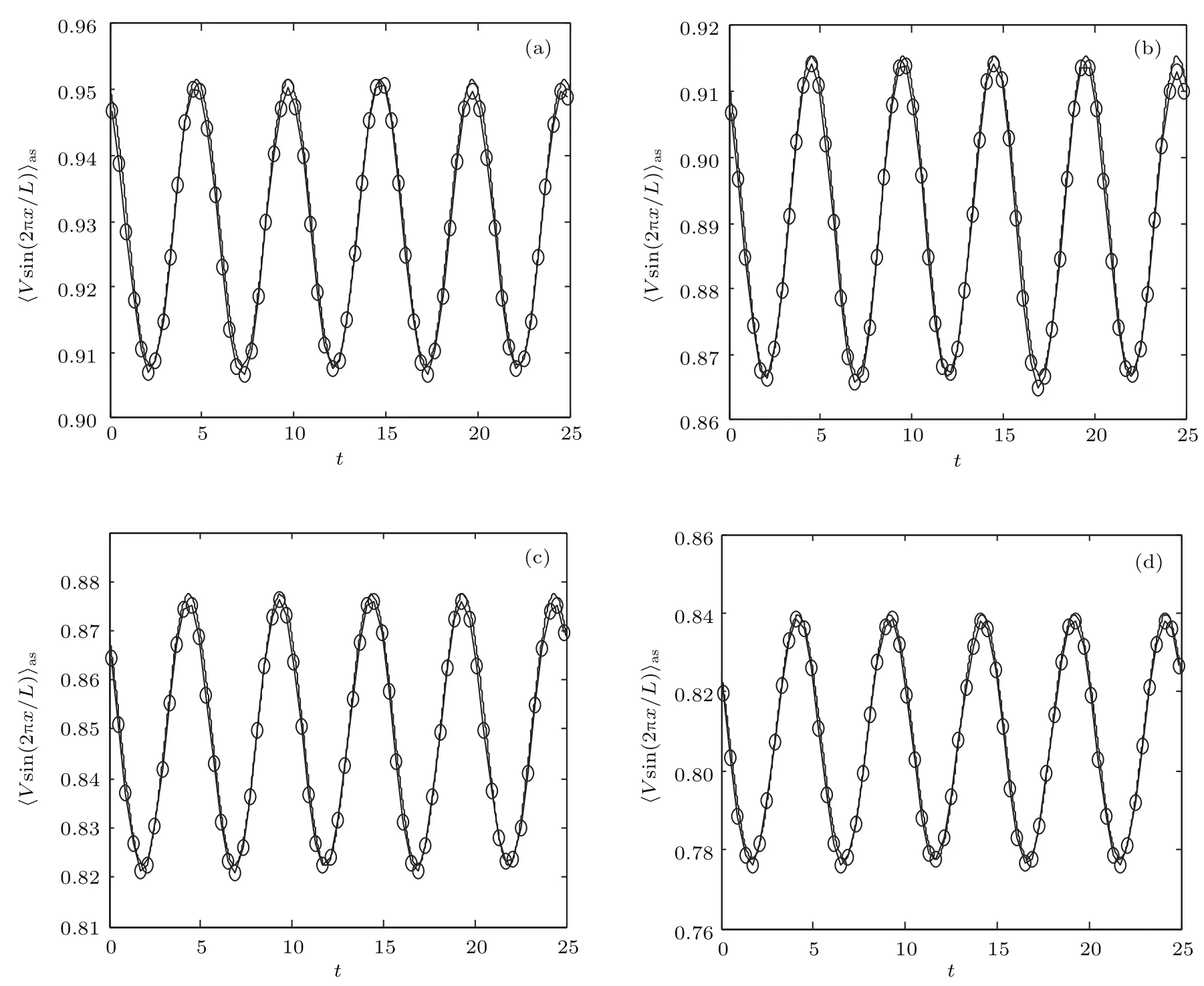
图2 系统的长时间总体均值响应(矩方法(实线)、直接模拟法(圆圈)),其中,参数D=0.2,Ω =0.4π,V=1.5,L=2π,ε=0.05;b为(a)0.95V,(b)V,(c)1.05V,(d)1.1VFig.2.The long time ensemble averages calculated from stochastic simulation(circle)and the method of moments(solid line).The parameter b corresponds to(a)0.95V,(b)V,(c)1.05V,and(d)1.1V,respectively,when D=0.2,Ω =0.4π,V=1.5,L=2π,and ε =0.05.
由文献[27]可知,系统的m阶线性敏感性可由未扰随机系统的平稳矩表示为
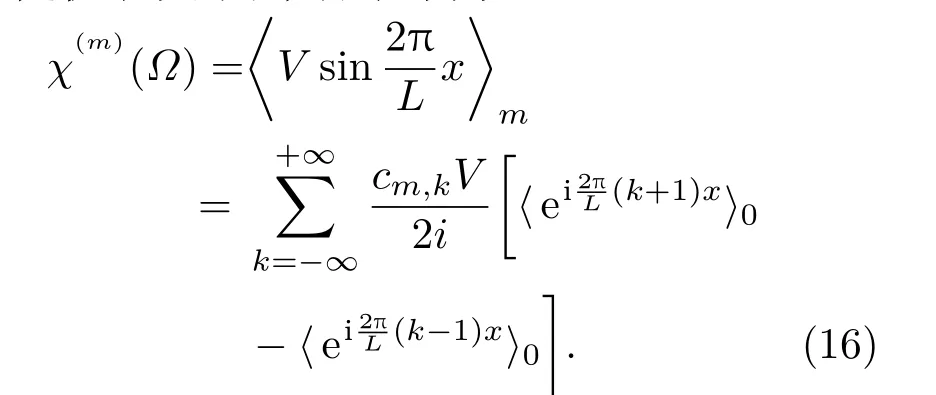
系统的长时间线性响应可以表示为
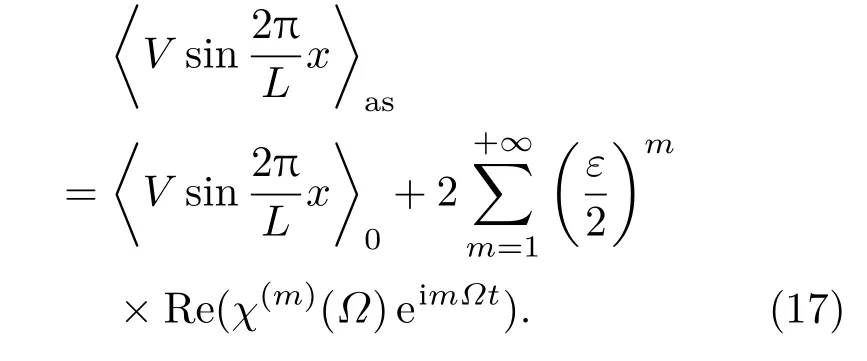
为了求解方程(14),必须选择一个截断阶K使得|k|6 K,计算结果表明,当K取16之后的值时,结果没有明显变化,因此取K=16展示数值结果.为了验证基于扰动展开法的矩方法的精确性,我们用Box-Muller随机数算法[28]生成高斯白噪声,在此基础上用欧拉算法对系统(2)进行直接模拟,并将该直接模拟的结果与矩方法计算所得结果进行比较.图2给出了两种方法计算的系统的长时间总体均值响应,可见数值模拟与矩方法所得的结果几乎完全符合,这说明了矩方法的有效性.
3 基于非扰动展开法的矩方法
对于任意ε,根据Floquet理论,FP方程(4)的长时间解是时间的周期函数,其周期与输入周期信号相同,即考虑到长时间解的周期性,可将其按傅里叶级数展开[29,30]
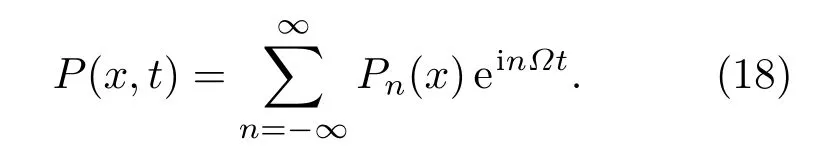
将展(18)式代入方程(6),有
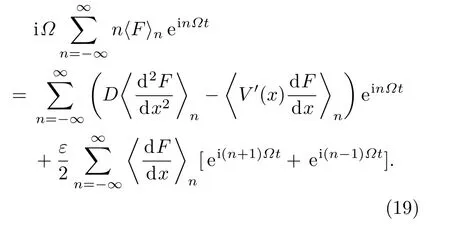
利用三角函数系的正交性得
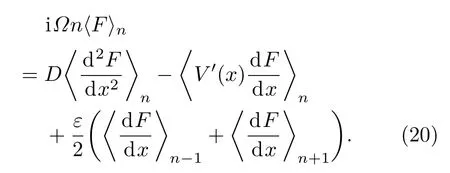
下面过程和线性响应的计算相似.考虑到未知函数Pn(x)必须满足周期边界条件,把它展成如下形式的三角级数:
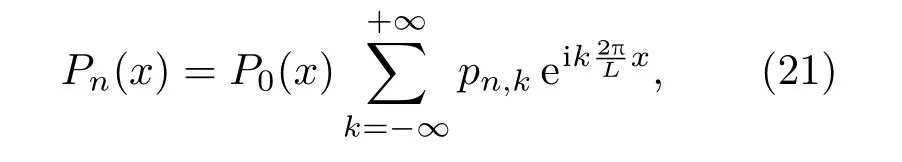
有p0,k=δ0,k,将展(21)式代入方程(20)并且选取有

其中l=0时概率规范化性质自然满足.
系统n阶响应敏感性可由未扰随机系统的平稳矩表示为
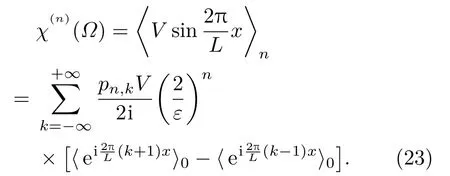
系统的长时间响应可以表示为
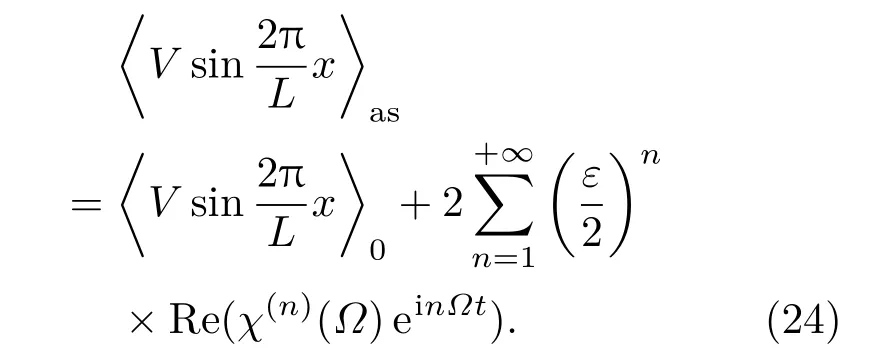
选取截断阶N=10,K=16,应用高斯块消去法,对方程(22)进行求解,并且为了验证基于非扰动展开法的矩方法的准确性,图3给出了矩方法和直接模拟法得到的系统(2)的长时间总体均值响应.由图3可见,这两种方法所得结果符合程度较高,这表明了该方法在计算系统响应时的有效性.
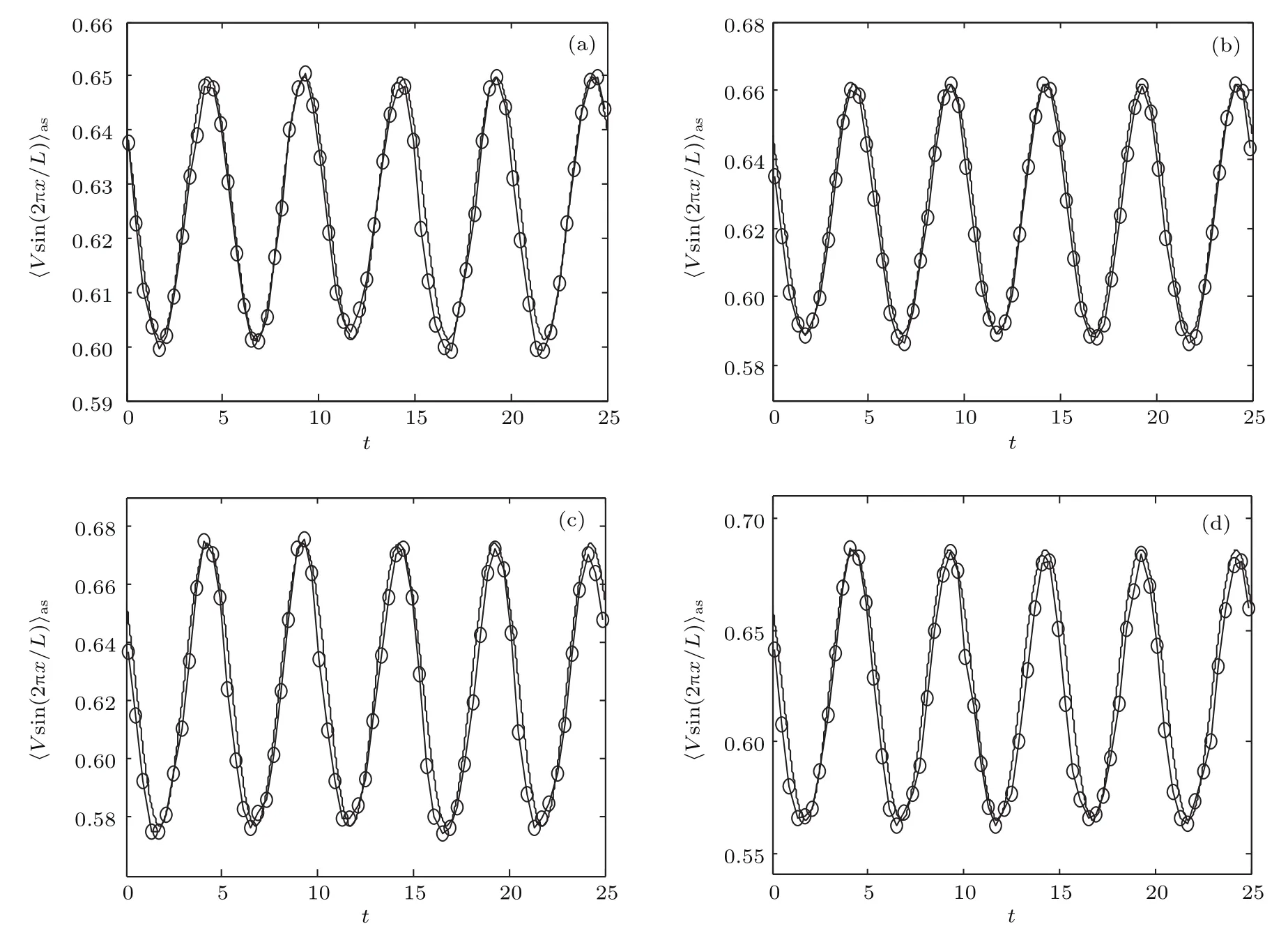
图3 系统的长时间总体均值响应(矩方法(实线)、直接模拟法(圆圈)),其中,参数D=0.6,Ω =0.4π,V=1.5,L=2π,b=V;ε为(a)0.1,(b)0.15,(c)0.2,(d)0.25Fig.3.The long time ensemble averages calculated from stochastic simulation(circle)and the method of moments(solid line).The parameter ε corresponds to(a)0.1,(b)0.15,(c)0.2,and(d)0.25,respectively,when D=0.6,Ω =0.4π,V=1.5,L=2π,and b=V.
4 搓板势系统的随机共振
这里选取前三阶谐波的谱放大因子|χ(n)|2,n=1,2,3作为观察系统(2)的随机共振现象的量化指标,图4和图5给出了在弱周期信号极限下,基于扰动展开法的矩方法计算的谱放大因子随噪声强度的演化曲线.由图4和图5中共振曲线的非单调性可知系统存在随机共振现象,且在一定的偏置范围内,随着偏置b的逐渐增加,共振曲线的峰值逐渐增加,而共振峰对应的噪声强度逐渐减小.对于充分大的阻尼,我们可以忽略惯性效应,在没有噪声时,质点将进行爬行运动.有噪声时质点在过阻尼搓板势系统中不会长时间停留在固定状态,而是会在某一时刻被“踢出”势阱,向与其相邻的更低的势阱运动.随机共振理论指出,当有噪声的系统发生随机共振时,部分噪声能量会转化为有用的信号能量.系统的势垒与系统、信号和噪声三者发生协同效应的条件有关,其高度揭示了系统按照信号的频率节奏产生跃迁、进入随机共振状态时信号和噪声所需的能量.势垒高度越低,意味着系统进入随机共振状态时所需能量越少.反之,所需的能量越多.当增大偏置b时,势垒高度会降低,即质点在向更低的势阱运动时所需的能量降低,从而由噪声引起的阱间跃迁更容易发生.
下面从随机系统的功率谱出发研究随机共振现象,考虑到b-sinx关于x的周期性,采用{sinx(t)}的功率谱描述系统响应,其定义如下[31]:
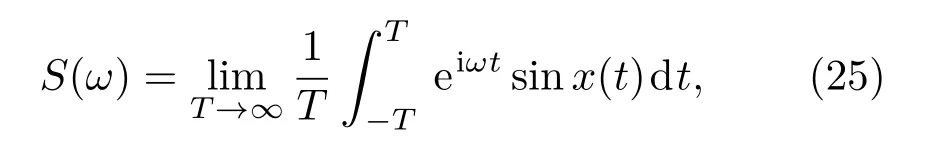
其中功率谱S(ω)在计算时取为1000次实验的平均值.随机共振作为周期信号和噪声之间的一种协作效应,系统(2)若存在随机共振现象,则其输出响应具有和输入周期信号相同的频率,即系统的功率谱在驱动频率处应该有峰值,并且在随机共振的最优噪声强度处峰值最大.图6(a)和图6(b)分别给出了系统输出响应在频率f=0.2和f=0.4处的功率谱随噪声强度的演化.将图6(a)和图4(b)、图6(b)和图5(a)进行比较可以看出,从功率谱出发所得一阶谐波的最优噪声水平D=0.1、二阶谐波的最优噪声水平D=0.2和矩方法计算所得的一致.
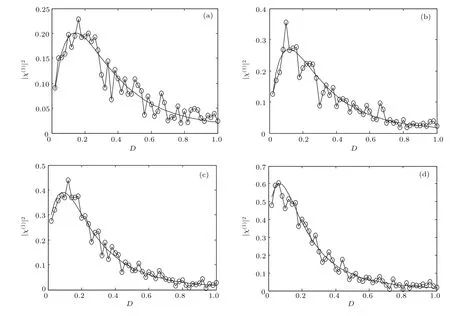
图4 一阶谐波功率谱放大因子随噪声强度的演化(矩方法(实线)、直接模拟法(圆圈)),其中,参数ε=0.05,Ω =0.4π,V=1.5,L=2π;b为(a)0.95V,(b)V,(c)1.05V,(d)1.1VFig.4.The dependence of the spectral ampli fi cation factor on the noise intensity at the fi rst harmonic:stochastic simulation(circle)and the method of moments(solid line).The parameter b corresponds to(a)0.95V,(b)V,(c)1.05V,and(d)1.1V,respectively,when Ω =0.4π,V=1.5,L=2π,and ε =0.05.
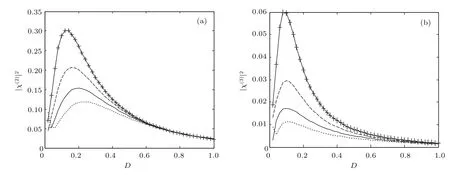
图5 (a)二阶谐波和(b)三阶谐波功率谱放大因子随噪声强度的演化,其中,参数Ω=0.4π,V=1.5,L=2π;b为0.95V(点线),V(实线),1.05V(短划线),1.1V(+)Fig.5.The dependence of the spectral ampli fi cation factor on the noise intensity at(a)the second harmonic and(b)the third harmonic.The parameter b corresponds to 0.95V(dotted line),V(solid line),1.05V(dashed line),and 1.1V(+),respectively,when Ω =0.4π,V=1.5,and L=2π.
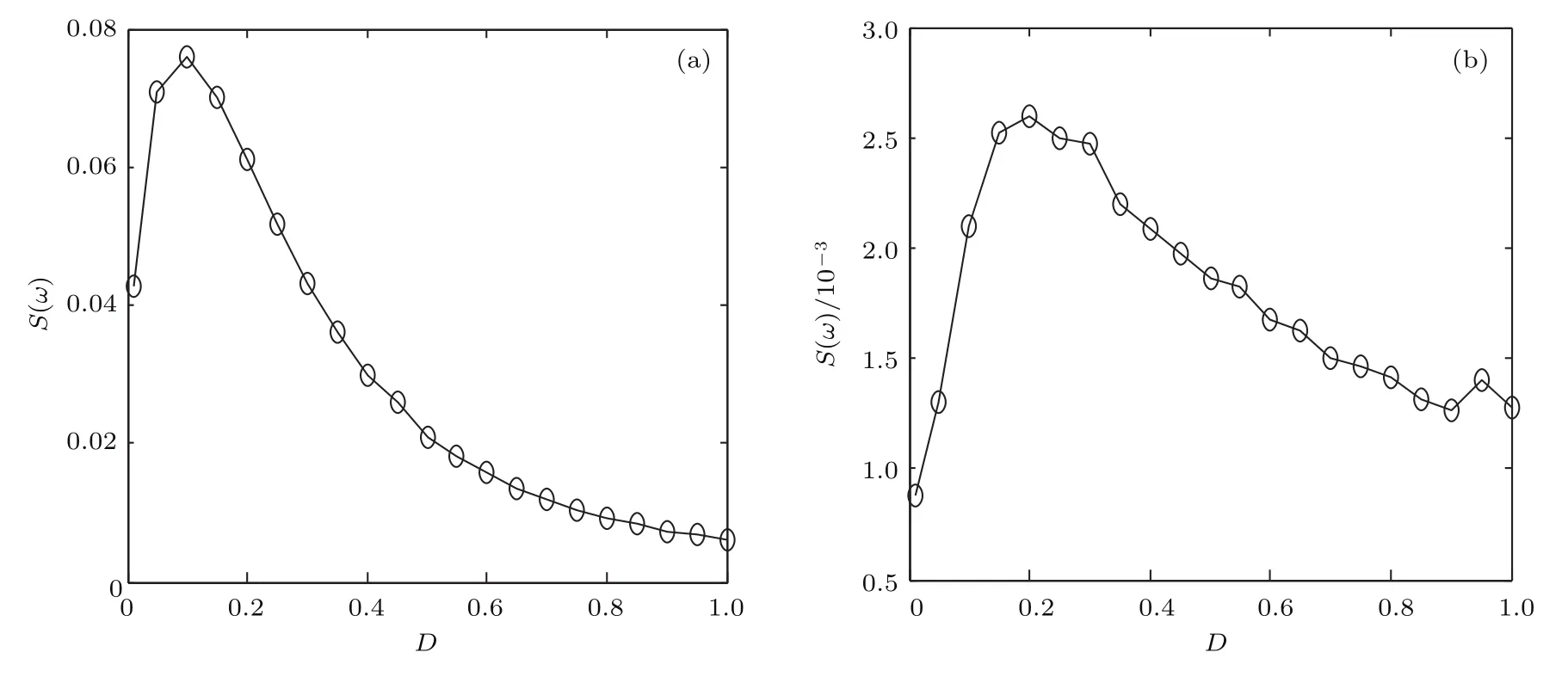
图6 系统输出响应在频率(a)f=0.2,(b)f=0.4处的功率谱随噪声强度的演化,其中,参数ε=0.05,Ω =0.4π,V=1.5,L=2π,b=VFig.6.The dependence of the power spectrum of the system output response on the noise intensity at the frequency(a)f=0.2,(b)f=0.4.The parameters ε=0.05,Ω =0.4π,V=1.5,L=2π,and b=V.

图7 一阶谐波功率谱放大因子随噪声强度的演化(矩方法(实线)、直接模拟法(圆圈)),其中,参数Ω =0.4π,V=1.5,L=2π,b=V;ε为(a)0.1,(b)0.15,(c)0.2,(d)0.25Fig.7.The dependence of the spectral ampli fi cation factor on the noise intensity at the fi rst harmonic:stochastic simulation(circle)and the method of moments(solid line).The parameter ε corresponds to(a)0.1,(b)0.15,(c)0.2,and(d)0.25,respectively,when Ω =0.4π,V=1.5,L=2π,and b=V.
为了进一步研究周期信号的幅值对随机共振效应的影响,在图7和图8展示了不同驱动幅值下由基于非扰动展开法的矩方法计算的系统(2)前三阶谐波的谱放大因子随噪声强度演化的结果.将该方法所得的一阶谐波的计算结果与直接模拟的结果进行比较,发现在ε 6 0.25的情况这两种方法符合较好,这验证了矩方法的有效性.由图7和图8可见,随着周期信号幅值的增大,随机共振效应会增强.周期信号幅值对系统随机共振效应的影响与偏置类似,增大周期信号的幅值相当于降低势垒高度,使得系统进入随机共振状态所需的能量降低,但是由于考虑的幅值远小于偏置,对势垒高度的改变并不明显,即所需能量的改变也不明显,所以增大幅值时,随机共振效应虽然有所增强,但对应的最优噪声强度并没有明显改变.为了得到基于非扰动展开法的矩方法的适用范围,采用均方差作为比较不同信号幅值下理论和数值计算差异性的量化指标,定量分析矩方法和随机模拟法所得结果的差异性.图9给出了均方差随信号幅值的演化,由图可见当ε 6 0.25时误差小于0.1%,这说明矩方法的适用范围是ε 6 0.25.
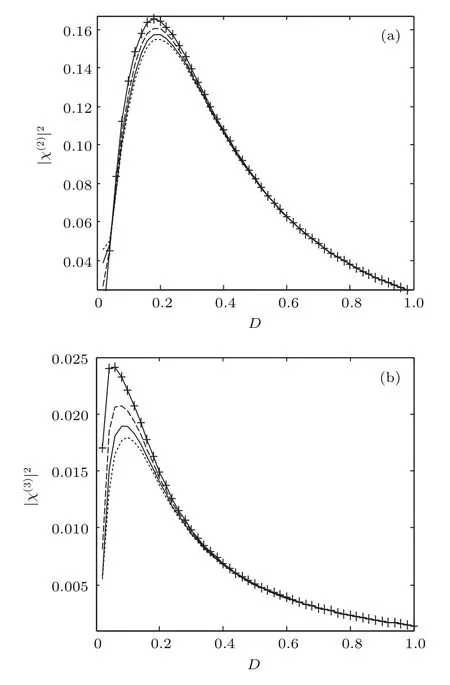
图8 (a)二阶谐波和(b)三阶谐波功率谱放大因子随噪声强度的演化,其中,参数Ω =0.4π,V=1.5,L=2π,b=V;ε为0.1(点线),0.15(实线),0.2(短划线),0.25(+)Fig.8.The dependence of the spectral ampli fi cation factor on the noise intensity at(a)the second harmonic and(b)the third harmonic.The parameter ε corresponds to 0.1(dotted line),0.15(solid line),0.2(dashed line),and 0.25(+),respectively,whenΩ =0.4π,V=1.5,L=2π,and b=V.
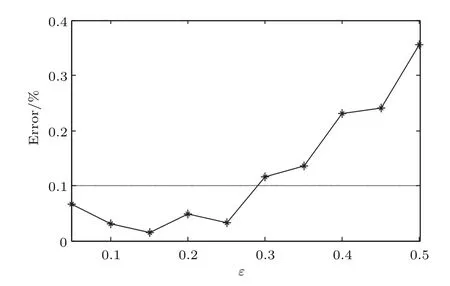
图9 均方差随信号幅值的演化,其中,参数Ω=0.4π,V=1.5,L=2π,b=VFig.9.The dependence of the mean error on the amplitude of the periodic signal. The parametersΩ =0.4π,V=1.5,L=2π,and b=V.
5 结 论
目前,对过阻尼搓板势系统的研究大多基于直接模拟法,花费时间较多,因此,本文采用矩方法研究受周期信号和高斯白噪声激励的过阻尼搓板势系统中的随机共振现象,研究工作表明在适当的参数条件下,过阻尼搓板势系统中存在随机共振现象.在线性响应意义下,采用谱放大因子作为随机共振现象的量化指标,基于扰动级数展开法的矩方法和直接模拟法所得的谱放大因子随噪声强度的演化曲线得到很好的拟合,这说明了矩方法的有效性.周期信号较大时,我们给出了基于非扰动展开法的计算系统非线性响应的矩方法,展示了前三阶谐波谱放大因子的计算结果,将该方法所得的一阶谐波的计算结果和直接模拟的结果进行了比较,验证了矩方法的有效性,并且通过采用均方差作为比较这两种方法在不同信号幅值下差异性的量化指标,得到矩方法的适用范围是ε 6 0.25.而且在一定范围内共振曲线的峰值随偏置参数的增大而增大,随机共振效应随驱动幅值的增大而增强.搓板势系统对于研究超离子导体的导电性、约瑟夫森结中超电流的波动、ad-原子在晶体表面的运动等物理问题具有现实针对性.本文所得的谱放大因子的适用范围突破了以往绝热近似条件和线性响应条件[16,17]的限制,使得矩方法在更广泛的参数范围下都有效,接下来我们将把这种方法推广到欠阻尼的情况.
[1]Benzi R,Sutera A,Vulpiani A 1981 J.Phys.A 14 L453
[2]Gammaitoni L,Hanggi P,Hung P,Marchesoni F 1998 Rev.Mod.Phys.70 223
[3]McNamara B,Wiesenfeld K,Roy R 1988 Phys.Rev.Lett.60 2626
[4]Paulsson J,Ehrenberg M 2000 Phys.Rev.Lett.84 5447
[5]Leonard D S,Reichl L E 1994 Phys.Rev.E 49 1734
[6]Mao X M,Sun K,Ouyang Q 2002 Chin.Phys.11 1106
[7]Zhang G L,Lü X L,Kang Y M 2012 Acta Phys.Sin.61 040501(in Chinese)[张广丽,吕希路,康艳梅 2012物理学报61 040501]
[8]Jiao S B,Ren C,Huang W C,Liang Y M 2013 Acta Phys.Sin.62 210501(in Chinese)[焦尚彬,任超,黄伟超,梁炎明2013物理学报62 210501]
[9]Wallace R,Wallace D,Andrews H 1997 Environ.Plan.A 29 525
[10]Asaklil A,Boughaleb Y,Mazroui M,Chhib M,Arroum L E 2003 Solid State Ion.159 331
[11]Falco A M 1976 Amer.J.Phys.44 733
[12]Hanggi P,Talkner P,Borkovec M 1990 Rev.Mod.Phys.62 251
[13]Kim Y W,Sung W 1998 Phys.Rev.E 57 R6237
[14]Dan D,Mahato M C,Jayannavar A M 1999 Phys.Rev.E 60 6421
[15]Tu Z,Lai L,Luo M K 2014 Acta Phys.Sin.63 120503(in Chinese)[屠浙,赖莉,罗懋康 2014物理学报 63 120503]
[16]Fronzoni L,Mannela R 1993 J.Stat.Phys.70 501
[17]Marchesoni F 1997 Phys.Lett.A 231 61
[18]Saikia S,Jayannavar A M,Mahato M C 2011 Phys.Rev.E 83 061121
[19]Reenbohn W L,Pohlong S S,Mahato M C 2012 Phys.Rev.E 85 031144
[20]Saikia S 2014 Physica A 416 411
[21]Liu K H,Jin Y F 2013 Physica A 392 5283
[22]Ma Z M,Jin Y F 2015 Acta Phys.Sin.64 240502(in Chinese)[马正木,靳艳飞 2015物理学报 64 240502]
[23]Risken H 1989 The Fokker Planck Equation(Berlin:Springer)pp287–289
[24]Monnai T,Sugita A,Hirashima J,Nakamura K 2006 Physica D 219 177
[25]Kang Y M,Jiang Y L 2008 Chin.Phys.Lett.25 3578
[26]Kang Y M,Jiang J,Xie Y 2011 J.Phys.A:Math.Theor.44 035002
[27]Evistigneev M,Pankov V,Prince R H 2001 J.Phys.A:Math.Gen.34 2595
[28]Fox R F,Gatland I R,Vemuri G,Roy R 1988 Phys.Rev.A 38 5938
[29]Jung P 1993 Phys.Rep.234 175
[30]Asish K D 2015 Physica D 303 1
[31]Qian M,Wang G X,Zhang X J 2000 Phys.Rev.E 62 6469
PACS:05.45.–a,05.40.–a,05.45.Mt,05.40.CaDOI:10.7498/aps.66.120501
Stochastic resonance in overdamped washboard potential system∗
Xie Yong1)†Liu Ruo-Nan2)
1)(State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,Xi’an 710049,China)
2)(School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an 710049,China)
10 February 2017;revised manuscript
21 March 2017)
Brownian motion in a washboard potential has practical signi fi cance in investigating a lot of physical problems such as the electrical conductivity of super-ionic conductor,the fl uctuation of super-current in Josephson junction,and the ad-atom motion on crystal surface.In this paper,we study the overdamped motion of a Brownian particle in a washboard potential driven jointly by a periodic signal and an additive Gaussian white noise.Since the direct simulation about stochastic system is always time-consuming,the purpose of this paper is to introduce a simple and useful technique to study the linear and nonlinear responses of overdamped washboard potential systems.In the limit of a weak periodic signal,combining the linear response theory and the perturbation expansion method,we propose the method of moments to calculate the linear response of the system.On this basis,by the Floquet theory and the non-perturbation expansion method,the method of moments is extended to calculating the nonlinear response of the system.The long time ensemble average and the spectral ampli fi cation factor of the fi rst harmonic calculated from direct numerical simulation and from the method of moments demonstrate that they are in good agreement,which shows the validity of the method we proposed.Furthermore,the dependence of the spectral ampli fi cation factor at the fi rst three harmonics on the noise intensity is investigated.It is observed that for appropriate parameters,the curve of the spectral ampli fi cation factor versus the noise intensity exhibits a peaking behavior which is a signature of stochastic resonance.Then we discuss the in fl uences of the bias parameter and the amplitude of the periodic signal on the stochastic resonance.The results show that with the increase of the bias parameter in a certain range,the peak value of the resonance curve increases and the noise intensity corresponding to the resonance peak decreases.With the increase of the driven amplitude,comparing the changes of the resonance curves,we can conclude that the e ff ect of stochastic resonance becomes more prominent.At the same time,by using the mean square error as the quantitative indicator to compare the di ff erence between the results obtained from the method of moments and from the stochastic simulation under di ff erent signal amplitudes,we fi nd that the method of moments is applicable when the amplitude of the periodic signal is lesser than 0.25.
stochastic resonance,linear response theory,Floquet theory,the method of moments
10.7498/aps.66.120501
∗国家自然科学基金(批准号:11672219,11372233)资助的课题.
†通信作者.E-mail:yxie@mail.xjtu.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.11672219,11372233).
†Corresponding author.E-mail:yxie@mail.xjtu.edu.cn
