一种通用的卫星导航信号码时延估计误差评估方法∗

刘桢张嘉怡 陆明泉 黄洁 赵拥军

1)(信息工程大学导航与空天目标工程学院,郑州 450001)

2)(清华大学电子工程系,北京 100084)

一种通用的卫星导航信号码时延估计误差评估方法∗

刘桢1)†张嘉怡2)陆明泉2)黄洁1)赵拥军1)

1)(信息工程大学导航与空天目标工程学院,郑州 450001)

2)(清华大学电子工程系,北京 100084)

(2017年3月13日收到;2017年4月6日收到修改稿)

卫星导航信号的码时延估计误差是决定系统服务性能的关键因素,迫切需要对多种不同调制与复用方式的导航信号进行全面的码时延估计误差性能评估,从而为后期的系统应用提供重要的选择依据.为此,本文提出了通用的码时延估计误差评估方法.首先,概括了导航接收机的码跟踪环路模型,根据是否匹配接收以及是否相干处理,将目前的导航接收机归纳为四种类型.其次,在假设码时延估计误差非常小的条件下,分别给出了匹配接收下相干处理和非相干处理时的估计误差以及相互之间的关系;推导了非匹配接收下非相干处理时的估计误差,并讨论了与相干处理时的关系.最后,推导了码时延估计误差的齐夫-扎凯界限,解决了估计误差不满足非常小这一假设条件时的评估.本文提出的评估方法均以导航信号的功率谱密度表示,为信号设计和接收机的研制提供了重要的理论指导,同时也给具体信号的评估带来了极大便利.仿真实验中对新一代典型导航信号的码时延估计误差做了有效评估.

卫星导航信号,码时延估计误差,评估方法

1 引 言

卫星导航系统能够为用户提供高质量的定位、导航和授时(positioning,navigation and timing,PNT)服务,在国防、航空、金融以及电力等众多领域获得了非常广泛的应用,并展现出了巨大的军事价值和经济价值[1,2].随着卫星导航应用领域的不断拓展,军民用户对PNT性能的需求不断提高,而采用更加先进的导航信号调制与复用技术是提升PNT性能的关键[3].因此,在新一代卫星导航系统升级与建设的需求下,导航信号调制与复用技术取得了重大进展.截至目前,已提出了多种单个信号分量的调制方式[4−13]和多路信号分量的恒包络复用方法[14−18],新的信号体制仍在陆续提出,迫切需要对这些信号的码时延估计误差性能做出有效评估,进而为接下来各系统的选用提供重要的参考依据.因此,需要建立完善的卫星导航信号码时延估计误差性能评估方法.

码时延估计误差的大小不仅与信号体制有关,与卫星导航接收机的接收模式和码跟踪环路的处理方式也紧密相关.新一代卫星导航接收机的接收模式可分为两种类型:一种是继续采用传统的完整接收模式,参考信号与接收信号相同,即匹配接收.理论上该接收模式下可以得到最佳的码跟踪性能,但是在处理二进制偏移载波(binary o ff set carrier,BOC)类信号时存在码跟踪模糊的问题,会导致严重的错误结果;另一种是参考信号与接收信号不再相同,即非匹配接收.目前,非匹配接收模式在BOC类信号处理中得到了广泛应用.为了消除跟踪模糊问题,通常用传统的二进制相移键控(binary phase shifting keying,BPSK)信号作为参考信号只接收BOC类信号的其中一个边带[19−22],或者通过构造特殊的参考信号实现两个边带的综合接收[23−25].另外,为了降低接收机的带宽以及复杂度,有时也用低阶的BOC信号接收高阶的BOC类信号,如用BOC(1,1)信号接收复用BOC(multiplex BOC,MBOC)(6,1,1/11)信号[26,27],所需带宽仅为原来的六分之一.无论是匹配模式还是非匹配模式的导航接收机,它们的码跟踪环路都包括相干处理和非相干处理两种情况.因此,导航接收机总共可划分为四种类型:匹配模式下相干处理、匹配模式下非相干处理、非匹配模式下相干处理以及非匹配模式下非相干处理.由于每种类型下的码时延估计误差都不相同,因而需要给出每种类型下的码时延估计误差评估方法.文献[28,29]分别推导了匹配模式下相干和非相干处理时的码时延估计误差,其中文献[28]也推导了码时延估计误差的克拉美罗下界(Cramér-Rao lower bound,CRLB),文献[30]推导了非匹配模式下相干处理时的码时延估计误差,这些结果得到了广泛应用.但是,目前还没有文献对非匹配模式下非相干处理时的码时延估计误差进行研究,也没有给出适合各种条件的码时延估计误差评估方法.

为此,本文推导了非匹配模式下非相干处理时的码时延估计误差,并分别讨论了在不同噪声环境以及码环间隔下同其他三种类型码时延估计误差之间的关系.上述四种类型的结果都是在码时延估计误差非常小这一假设条件下推导而来,但在复杂环境下载噪比较低时,码时延估计误差并不满足假设条件,此时就无法应用上述的结果进行评估.因此,本文又推导了导航信号码时延估计误差的齐夫-扎凯界(Ziv-Zakai bound,ZZB),ZZB的推导不需要码时延估计误差非常小的假设条件,很好地解决了低载噪比条件下码时延估计误差的评估.因此,结合已有的成果,本文给出了适用于各种情况的码时延估计误差评估方法,所有的误差表达式均以导航信号的功率谱密度表示,给具体信号的评估带来了很大方便.

本文第2部分给出了基带接收信号模型;第3部分给出了接收机码跟踪环路模型;第4部分推导了非匹配模式下导航信号的码时延估计误差;第5部分推导了码时延估计误差的ZZB;第6部分为仿真分析;最后为结论.

2 基带接收信号模型

不同调制方式的导航信号经过接收机前端滤波后,基带信号均可表示为

式中,s(t)为导航信号,其扩频码可能经过导航电文或二次码的调制,平均功率和归一化功率谱密度分别为Cs和Gs(f),即为码时延,取值在0到一个码片Tc之间;θ为载波初始相位,在[0,2π]上均匀分布;w(t)=n(t)+l(t)为噪声,其中n(t)是双边功率谱密度为N0/2的高斯白噪声,l(t)是功率谱密度为ClGl(f)的窄带干扰,即

3 接收机码跟踪环路模型

现代导航接收机中码跟踪环路通常采用延迟锁定环(delay lock loop,DLL),包括相干延迟锁定环(coherent DLL,CDLL)和非相干延迟锁定环(non-coherent DLL,NDLL)两种类型,分别对应相干处理和非相干处理,实际应用根据具体的信号环境而定[1].图1给出了典型的码跟踪环路模型.

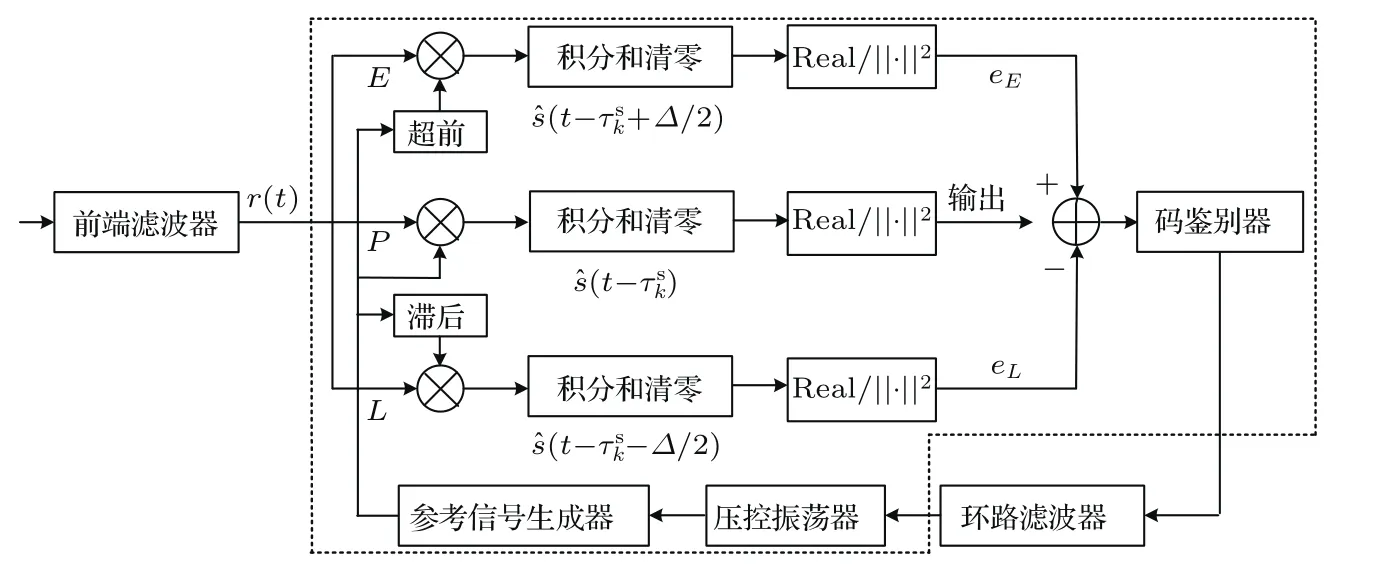
图1 典型的导航接收机码跟踪环路模型Fig.1.Model of typical navigation receiver’s code tracking loop.

图1模型中,实部Real和模的平方∥·∥2分别对应CDLL和NDLL.根据基带接收信号r(t)与参考信号ˆs(t)是否相同分为匹配接收模式和非匹配接收模式.将图1中的虚线部分抽象为开环估计器以后,可得到图2的等效模型.

图2 典型导航接收机码跟踪环路的等效模型Fig.2. Equivalent model of typical navigation receiver’s code tracking loop.

图2模型中,开环与闭环之间的关系更加清晰.讨论码时延估计误差的前提是码跟踪环路是收敛的,通常对收敛的保守估计方法是:三倍的码时延估计误差均方差不得超过鉴别器牵入范围的一半[1],即

(2)式中σtDLL为热噪声均方差,Re为码环受到的动态引力误差,d为鉴别器牵入范围的一半.需要注意的是(2)式假定码环未受载波环的辅助,当载波环辅助时范围会更大,具体可参考文献[1].文献[28]推导了平滑估计量的方差与未平滑估计量的方差之间的关系为

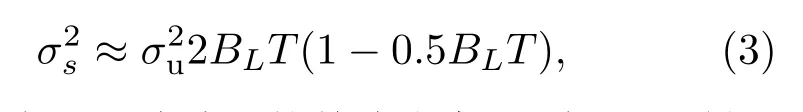
其中,BL为平滑滤波器的单边带宽,T为积分时间.(3)式为码时延估计误差的推导提供了极大便利.文献[28]中分别推导了码时延估计误差的CRLB以及匹配接收模式下采用CDLL时的码时延估计误差,其表达式分别为

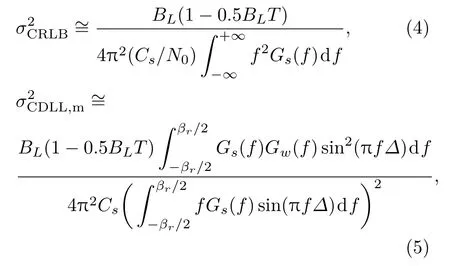
(5)式中∆为码环间隔.文献[29]中推导了匹配接收模式下采用NDLL时的码时延估计误差:

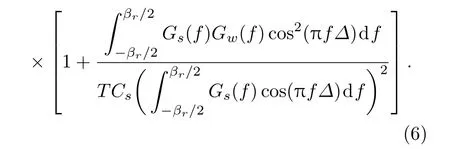
(4)式反映了导航信号所能达到的最高理论测距精度,其中,积分项称为Gabor带宽,反映信号本身的测距能力.Gabor带宽值越大,信号的测距精度越高,这为导航信号设计指明了一个目标,就是使得信号的功率谱密度尽可能多地占用通带内的高频分量.文献[13]提出了Gabor带宽的最优化方法.

4 非匹配模式下导航信号的码时延估计误差

4.1 相干处理时导航信号的码时延估计误差

针对相干处理的情况,文献[30]推导了白噪声环境下的码时延估计误差,但存在干扰时的结果与其相似,下面给出存在干扰时的结果.

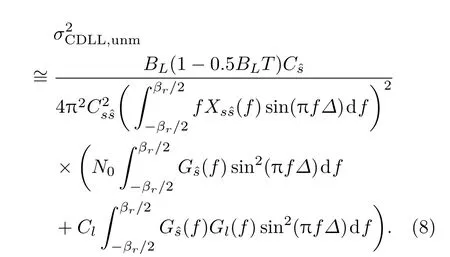
当噪声w(t)中不存在窄带干扰n(t)时,(8)式可以简化为

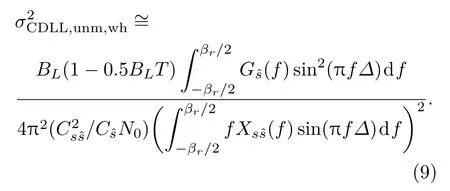
(10)式就是(5)式不含干扰时的结果,其中,CNR=Cs/N0表示载噪比,当码环间隔∆→ 0时,(10)式又可进一步简化为

此时(11)式退化为(4)式的结果,也就是码时延估计误差的CRLB.这说明随着码环间隔∆变小,码时延估计误差性能提高,主要是因为窄的码环间隔具有良好的抗多径能力,从而改善了码时延估计误差性能.但是实际中码环间隔∆不能太小,否则影响接收机的动态范围.对于任意的码环间隔∆,可以证明(11)式均小于(10)式.

4.2 非相干处理时导航信号的码时延估计误差

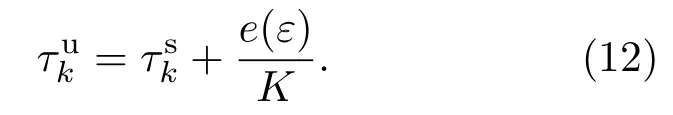
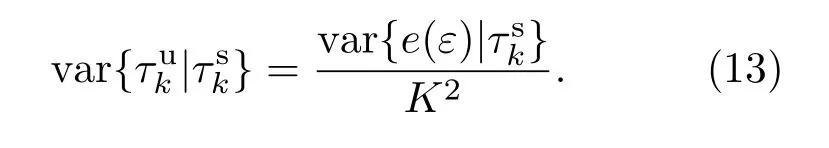
将附录A中的(A10)式代入(13)式后,化简可得

通过与(7)式的比较发现,(15)式中括号外的部分就是相干条件下的方差因此可进一步写为

当噪声w(t)中只含高斯白噪声时,Gw(f)=N0,结合(9)和(16)式可以表示为

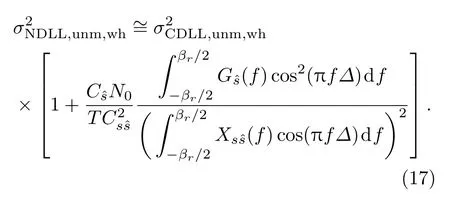
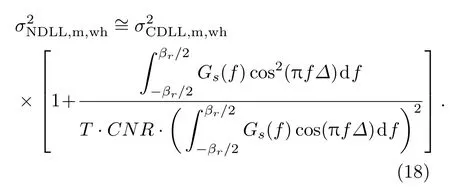
当码环间隔∆ → 0时,结合(11)和(17)式进一步简化为

从(16)—(19)式中可以看出,无论是否匹配接收、码环间隔是否趋于零以及噪声是否为高斯噪声,非相干处理与相干处理时的码时延估计误差都存在相似的关系,即非相干处理时的误差σ2NDLL等于相干处理时的误差σ2CDLL与因式[1+αSL]的乘积,其中因式αSL为非相干处理带来的平方损耗.

上述讨论的各种误差结果,均是在假设码时延估计误差非常小的条件下推导而来.如本文结果的推导中,在附录A的(A6)式向(A7)式的推导过程中就需要用到假设条件.上述各种结果的推导均基于相同的假设条件,下面对其进行近似:

(20)式中的两个近似等式可看作是等价的.因此,由sin(x)的泰勒级数可得,当误差满足ε<1/(20πf)时,(20)式中的近似足够精确.由于前端滤波器的双边带宽为2βr,因此可以得到误差需要满足的条件为

需要注意的是,由于信号的功率谱密度Gs(f)在带宽外迅速衰减,因而带宽外的f2Gs(f)对Gabor带宽的贡献越来越小.因此,(21)式是最严格的条件,对于具体的导航信号,误差ε的条件会进一步放宽.当误差不满足假设条件时,上述结果均不再适用.从码时延估计误差的表达式也可以看出,码时延估计误差随着载噪比的减小而一直增加.但从导航信号捕获和跟踪环节来看,信号完成捕获后码时延的不确定度在半个码片以内,也就是说跟踪阶段的任何码误差应该小于半个码片.产生这种问题的原因在于码时延估计误差较大时,上述结果便不再成立.

5 码时延估计误差的ZZB

导航信号的码时延估计过程可以等效为一个对所有可能时延的判断过程.假设ˆt0为估计时延,接收信号s(t)是两个等概率信号s(t−x)或s(t−x−τ)中的一个,其中,x和x+τ分别表示两个等概率信号的时延.导航信号码时延的不确定范围在一个扩频码片持续时间Tc以内,因而x和x+τ的取值范围均为[0,Tc].因此,进行以下估计是合理的:

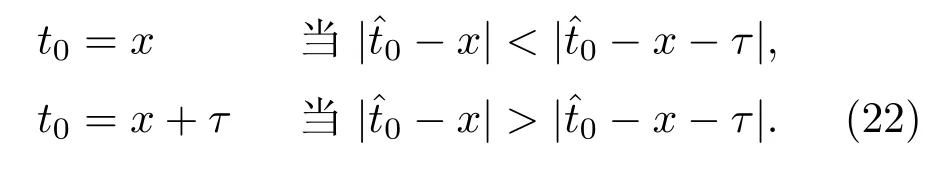
(22)式正好是一个二元假设检验问题,在平均错误概率最小条件下是最优的.当接收信号为r(t)=s(t−t0)+n(t)时,二元假设检验问题的最小错误概率可写为[31,32]

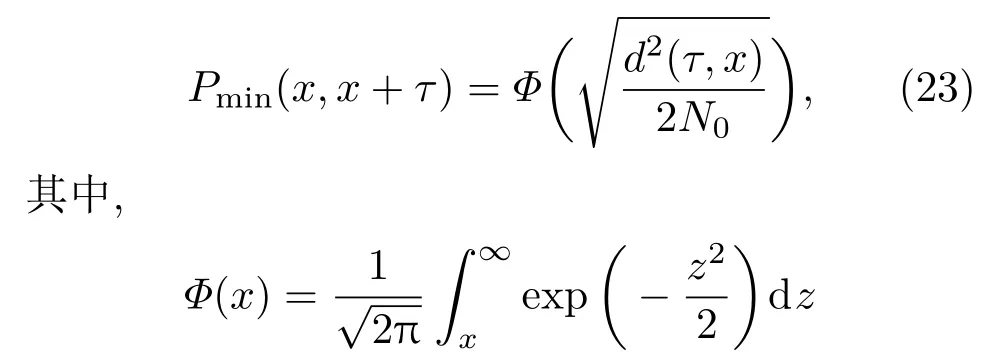
是标准正态分布的概率表述;d2(τ,x)表示信号之间的平均距离,

(24)式中,积分上限T表示信号的持续时间.在最小错误概率Pmin(x,x+τ)下,对于估计误差ε=t0−0,则估计过程中的均方误差可推导为[31,32]

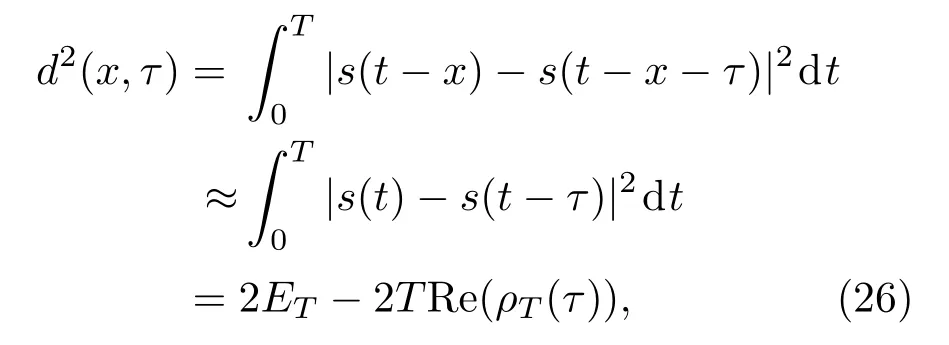
(26)式中ET表示T内信号s(t)的能量,

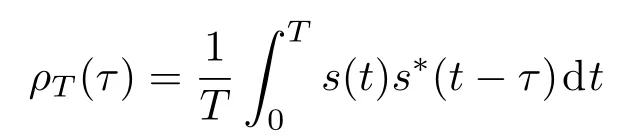
表示s(t)的自相关函数.假设信号s(t)的功率谱密度为CsGs(f),且满足

Gs(f)为偶函数,Cs为平均功率.由于自相关函数ρT(τ)与功率谱密度CsGs(f)是一对傅里叶变换对,因此可以得到下式:

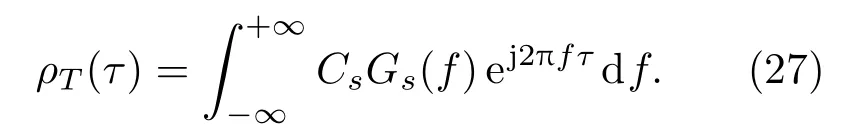
将(27)式代入(26)式中后可以得到

由于信号能量ET可写为以下形式:

将(29)式代入(28)式中后可进一步化简为

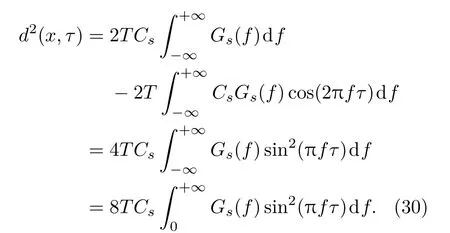
将(30)式代入(23)式后可得

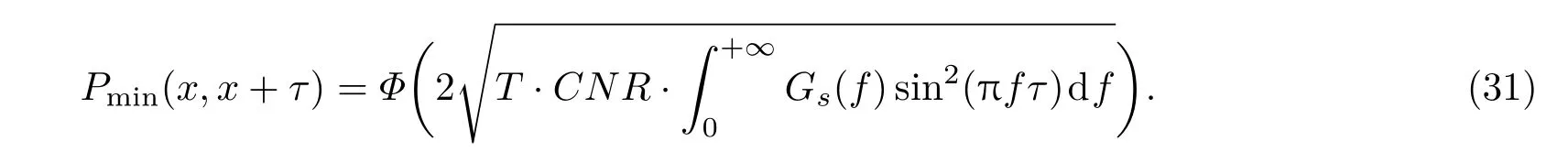
(31)式中CNR=Cs/N0代表载噪比,将(31)式代入(25)式后可得到码时延估计误差的ZZB的表达式为

由(32)式可以看出,当信号持续时间T越长、载噪比CNR越高时,ZZB的值就越小,即码时延估计误差越小,另外,因式

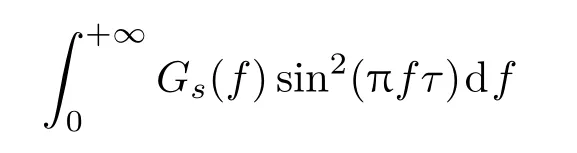
在一定程度上也表达了Gabor带宽的含义,但是与第3节和第4节的结果相比,都不再是直接的反比关系.假设载噪比CNR足够小时,即

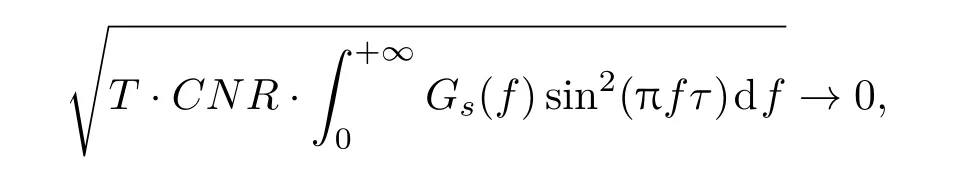
6 仿真分析

本文对典型导航信号的码时延估计误差进行评估,选用的信号包括已经得到应用的BOC(1,1),MBOC(6,1,1/11)和交替BOC(alternative BOC,AltBOC)(15,10)信号以及最新提出的非对称恒包络BOC(asymmetric constant envelope BOC,ACEBOC)(15,10)[17]和双极性副载波(bipolar subcarrier ACEBOC,BS-ACEBOC)(15,10)[18]信号,其中ACEBOC和BS-ACEBOC的功率分配比例设为P=[3,1,3,1],这两种方式是我国北斗三代系统B2频点的理想选择.仿真包括两个部分:一是匹配接收和非匹配接收时的误差;二是误差的ZZB.

仿真1匹配接收和非匹配接收时的误差

仿真以非相干处理为例,非匹配接收时采用BOC类信号的单边带BPSK-Like方法,参考信号为BPSK(1)和BPSK(10)信号,仿真中环路带宽BL=0.6 Hz,积分时间T=20 ms,码环间隔∆=0.8Tc.仿真中接收机带宽有多种设置:一是2,4,14以及24 MHz,用于低码速率信号,其中2 MHz用于BPSK(1)的匹配接收和BOC(1,1)和MBOC(6,1,1/11)的非匹配接收;4 MHz和14 MHz分别用于BOC(1,1)和MBOC(6,1,1/11)的匹配接收,24 MHz用于这两种信号码时延估计误差的CRLB计算;二是20,50以及90 MHz,用于高码速率信号,其中20 MHz用于BPSK(10)的匹配接收和AltBOC(15,10),ACEBOC(15,10)以及BSACEBOC(15,10)的非匹配接收,50 MHz和90 MHz分别用于这三种双频调制信号的匹配接收和码时延估计误差CRLB的计算.图3给出了各信号的Gabor带宽随接收机带宽变化的情况,图4和图5分别给出了低码速率和高码速率下码时延估计误差的均方差随载噪比的变化情况.

图3 (网刊彩色)Gabor带宽随接收机带宽的变化Fig.3.(color online)Gabor bandwidth variation with respect to receiver’s bandwidth.

从图3可以看出,对于低码速率信号,由于高频分量BOC(6,1)的存在,MBOC(6,1,1/11)的Gabor带宽最大,BPSK(1)的最小;对于高码速率信号,接收带宽在45 MHz以内或者在80—100 MHz之间时,BS-ACEBOC(15,10)具有一定的优势,而当接收带宽在45—80 MHz以内时,BS-ACEBOC(15,10)的Gabor带宽小于其他两种信号;在接收带宽的整个区间,ACEBOC(15,10)和AltBOC(15,10)的Gabor带宽相当;当接收带宽在20 MHz以内时,BPSK(10)的Gabor带宽大于三种复用信号的Gabor带宽,这主要是因为它们频谱的主瓣被搬移到中心频点的两侧.Gabor带宽决定着信号的码时延估计误差性能,Gabor带宽越大,码时延估计误差性能越好.图3中各信号的Gabor带宽能够帮助解释图4和图5的结果.

图4 (网刊彩色)低码速率信号的码时延估计误差随载噪比的变化Fig.4.(color online)Code delay estimation error of low code rate signals with respect to CNR.

从图4可以看出,MBOC(6,1,1/11)的码时延估计误差的CRLB和匹配接收时的码时延估计误差都明显优于BOC(1,1)信号,这主要是因为对于相应的接收带宽,MBOC(6,1,1/11)的Gabor带宽大于BOC(1,1)信号的Gabor带宽.但在2 MHz带宽下非匹配接收时,BOC(1,1)的码跟踪性能略优于MBOC(6,1,1/11),这与匹配接收和CRLB的结果正好相反.这是因为2 MHz带宽内MBOC(6,1,1/11)的BOC(6,1)高频分量被滤除了,只剩下了BOC(1,1)分量,此时剩余的功率分量没有单纯的BOC(1,1)大.与BPSK(1)匹配接收的结果相比,BOC(1,1)和MBOC(6,1,1/11)非匹配接收时码跟踪性能损失了约2 dB.

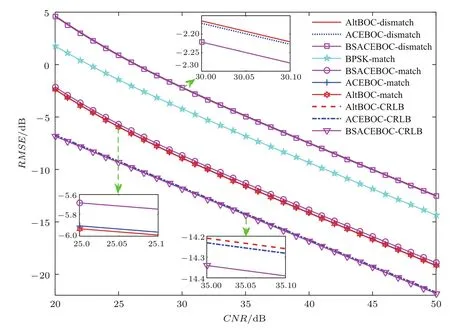
图5 (网刊彩色)高码速率信号的码时延估计误差随载噪比的变化Fig.5.(color online)Code delay estimation error of high code rate signals with respect to CNR.

从图5可以看出,带宽为90 MHz时,BSACEBOC(15,10)的码时延估计误差的CRLB小于其他两种信号,这是因为此时其Gabor带宽最大;但在匹配接收时BSACEBOC(15,10)的误差却最大,这是因为接收带宽为50 MHz时,BSACEBOC(15,10)的Gabor带宽小于其他两种信号;对于20 MHz带宽时的非匹配接收,BSACEBOC(15,10)的误差优于其他两种信号.需要注意的是,此时与BPSK(10)信号匹配接收的结果相比,三种复用信号的码跟踪性能损失了约3 dB.

结合图4和图5可以看出,采用单边带非匹配接收时,五种BOC类信号的码跟踪性能相比于相应的CRLB,性能均约有12 dB的损失;与匹配接收时的码跟踪性能相比,约有5—7 dB的性能损失;与参考信号匹配接收时的性能相比约有3 dB的性能损失.这些结论对于区间[20,50]dB·Hz内的任意载噪比都是成立的.非匹配接收时码跟踪性能损失的原因主要有三点:一是单边带接收造成3 dB的功率损失;二是非匹配接收使得BOC类信号的一些固有性能损失,如自相关函数展宽,这会导致测距精度的降低;三是BOC类信号功率谱密度的最大值并非恰好在与中心频点相距副载波频率的位置,而是在稍微靠近中心频点的位置,这就导致每个边带的主瓣与参考信号的主瓣并没有对齐,从而造成一定的性能损失.产生这种问题的主要原因是BOC类信号上下两个边带之间的相互影响所致.

总之,在BOC类信号的非匹配接收中,是以一定的码跟踪性能损失换取自相关函数模糊度的消除以及与传统信号处理架构的良好兼容,从而降低接收机的复杂度.目前,在一些非高精度要求的接收机中,非匹配接收处理得到了广泛应用.

仿真2误差的ZZB

仿真中为了突显低载噪比下ZZB的性能,载噪比的范围设置为[−20,40]dB·Hz,而目前接收机能达到的最低值约为10 dB·Hz.同时,为了与ZZB进行性能以及适用场合的分析比较,也给出了CRLB的仿真.

从图6可以看出,对于低码速率信号,当载噪比大于约22 dB·Hz时,ZZB和CRLB之间的差距变小并且保持稳定,当载噪比小于约22 dB·Hz时,两者之间的差距先增大然后减小,在载噪比约等于−13 dB·Hz时两者重合,随后ZZB趋于固定值而CRLB一直呈线性增加;高码速率信号具有与低码速率信号相似的结论,由于三路高码速率信号的功率谱非常接近,因而它们的ZZB和CRLB均呈现良好的一致性.当载噪比持续降低时,高码速率信号和低码速率信号的ZZB趋于相应的固定值.其中,BPSK(1),BOC(1,1)以及MBOC(6,1,1/11)趋于极限值19.5 dB,而AltBOC(15,10),ACEBOC(15,10)以及BS-ACEBOC(15,10)趋于极限值9.5 dB,这两个极限值正好满足理论界限而此时的CRLB则分别约为27 dB和35 dB,远远大于ZZB.

从图6和上述的分析可以得出ZZB和CRLB的应用场合:对于具体的导航信号,在大范围载噪比区间,如[−20,40]dB·Hz,根据其ZZB和CRLB的对数曲线可以得到它们之间的差距明显变大时对应的载噪比值,以此载噪比值为界限,当信号的载噪比大于或小于此值时,分别应用CRLB和ZZB对码时延估计误差进行评估.

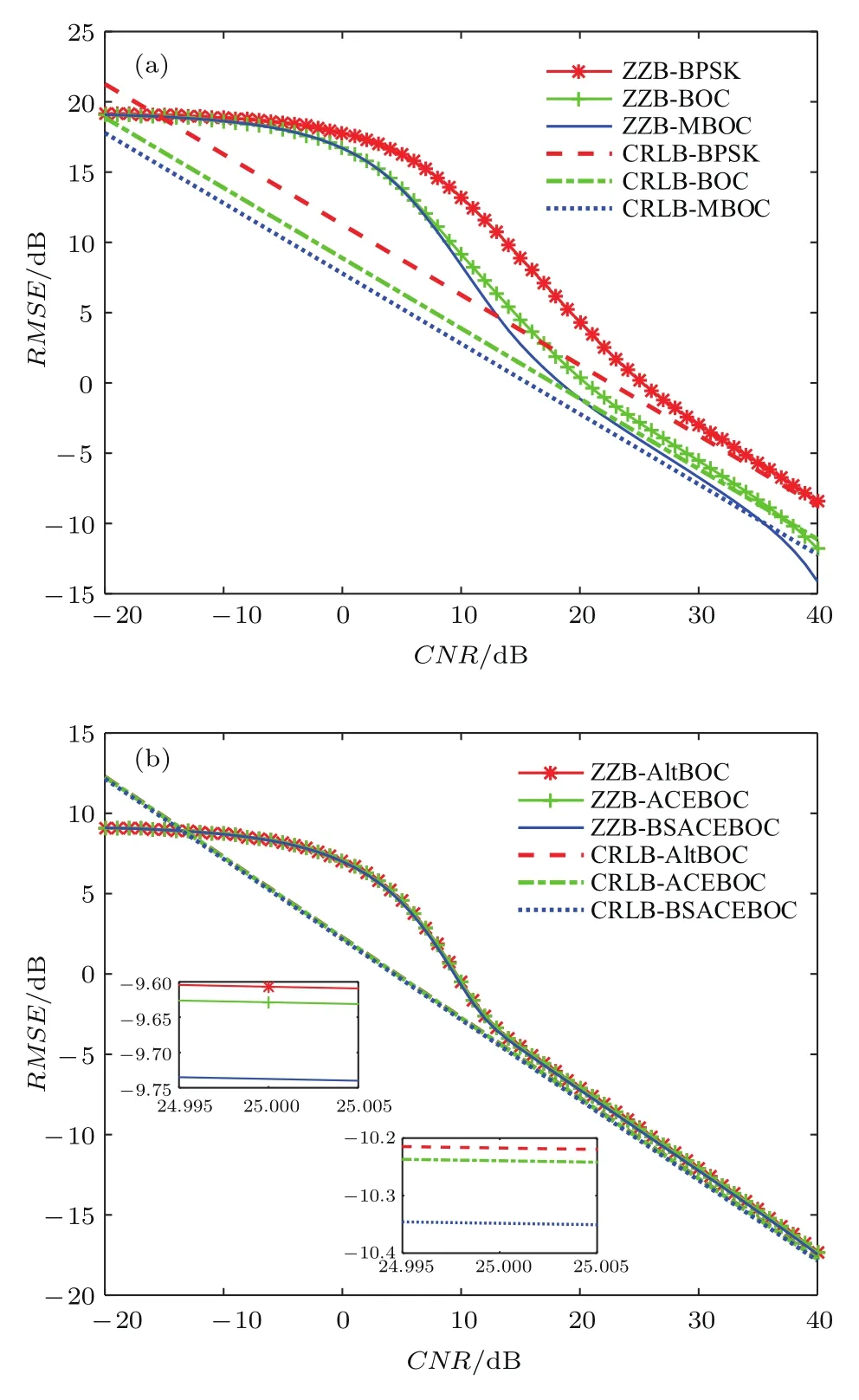
图6 (网刊彩色)码时延估计误差的ZZB和CRLB随载噪比的变化(a)低码速率信号;(b)高码速率信号Fig.6.(color online)The ZZB and CRLB of code delay estimation error with respect to CNR:(a)Low code rate signals;(b)high code rate signals.

7 结 论

本文根据目前导航接收机的结构,概括了码跟踪环路的等效模型,根据接收信号与参考信号是否匹配以及码跟踪环路中处理方式是否相干,将导航信号码时延估计误差的评估归纳为四种类型,在码时延估计误差满足非常小的假设条件下,推导了非匹配模式下非相干处理时的码时延估计误差,并讨论了同其他三种类型下码时延估计误差之间的关系.当码时延估计误差不满足非常小的假设条件时,推导了新的码时延估计误差界限,从而给出了适用于各种情况的码时延估计误差评估方法.仿真实验中对典型导航信号的码时延估计误差进行了评估,实验结果与理论分析完全符合.因此,本文方法能在未来导航信号设计以及我国北斗三代系统的信号遴选方面提供重要的指导.

附录A 非匹配接收模式下非相干处理时码时延估计误差的条件方差推导

非相干处理时,根据图1中的环路模型,此时码鉴别器的输入e为超前和滞后支路积分结果的模的平方的差,是k时刻码时延估计误差ε=t0−tsk的函数,其表达式可以写为

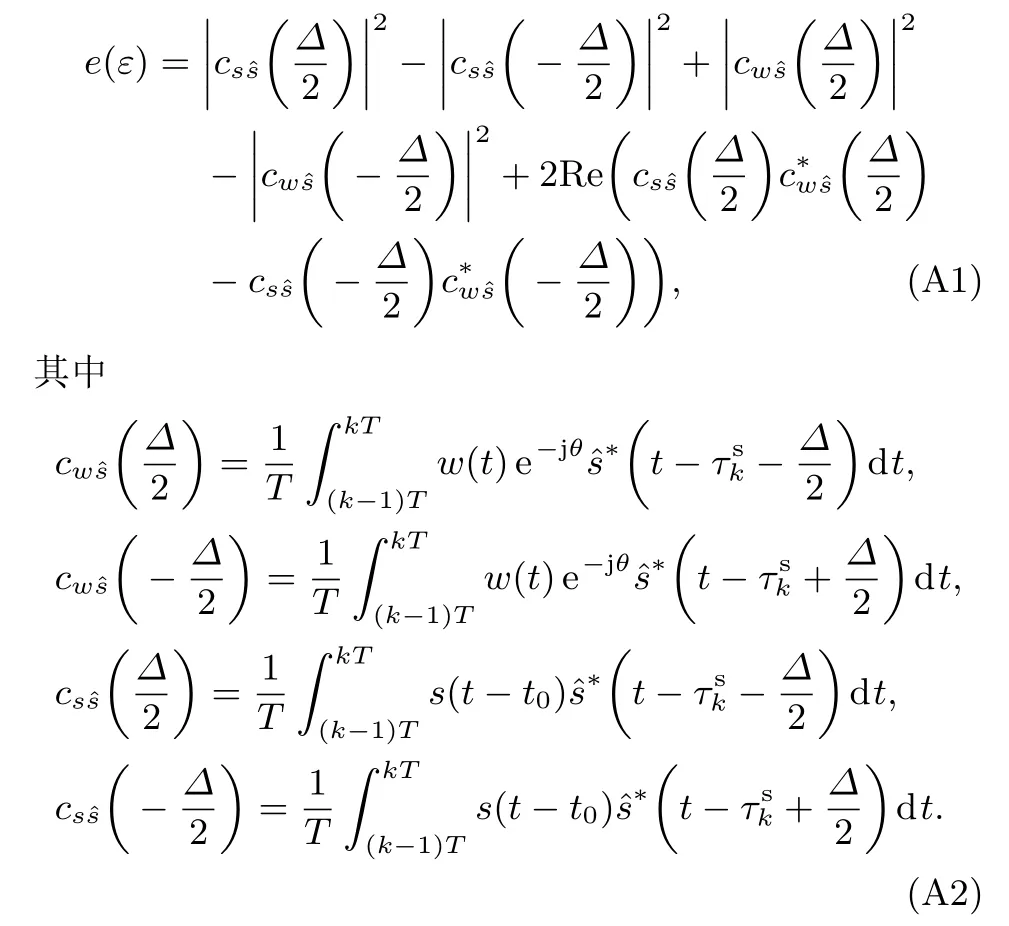
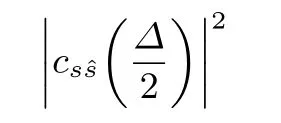
假设误差ε非常小,需要特别注意这一假设条件,不满足这一假设条件时需要重新讨论.在此假设条件下可认为cos(2πfε)≈ 1,sin(2πfε)≈ 2πfε,因此,(A6)式可进一步化简为

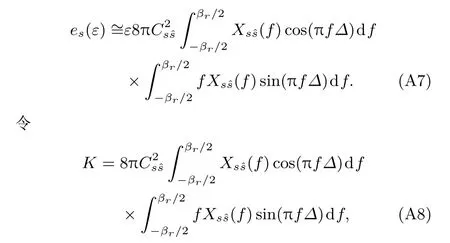
则K被称为鉴别因子,表示了码时延估计误差ε的放大倍数,因此,误差信号e(ε)可写为

经过一系列化简,可得到误差信号e(ε)的条件方差为

[1]Xie G 2009 GPS Principle and Receiver Design(Beijing:Electronic Industry Press)pp1–4(in Chinese)[谢钢 2009 GPS原理与接收机设计 (北京:电子工业出版社)第1—4页]

[2]Wang S Z,Zhu G W,Bai W H,Liu C L,Sun Y Q,Du Q F,Wang X Y,Meng X G,Yang G L,Yang Z D,Zhang X X,Bi Y M,Wang D W,Xia J M,Wu D,Cai Y R,Han Y 2015 Acta Phys.Sin.64 089301(in Chinese)[王树志,朱光武,白伟华,柳聪亮,孙越强,杜起飞,王先毅,孟祥广,杨光林,杨忠东,张效信,毕研盟,王冬伟,夏俊明,吴迪,蔡跃荣,韩英2015物理学报64 089301]

[3]Zhu Y H 2016 Ph.D.Dissertation(Beijing:Tsinghua University)(in Chinese)[朱永辉 2016博士学位论文 (北京:清华大学)]

[4]Yao Z,Lu M Q 2016 New Generation Satellite Navigation System Signal Design Principle and Implementation Technology(Beijing:Electronic Industry Press)pp15–20(in Chinese)[姚铮,陆明泉2016新一代卫星导航系统信号设计原理与实现技术 (北京:电子工业出版社)第15—20页]

[5]Betz J W 1999 Proceedings of the Institute of Navigation’s National Technical Meeting San Diego,USA,January 14–16,1999 p639

[6]Sun Z X,Yu Y,Zhou F,Liu S Z,Qiao G 2014 Acta Phys.Sin.63 104301(in Chinese)[孙宗鑫,于洋,周锋,刘凇佐,乔钢2014物理学报63 104301]

[7]Hegarty C J,Betz J W,Saidi A 2004 Proceedings of the 60th Annual Meeting of The Institute of Navigation Dayton,USA,June 7–9,2005 p56

[8]Hein G W,Avila-Rodriguez J A,Wallner S,Pratt A R,Owen J I R,Issler J L 2006 Proceedings of the International Technical Meeting of the Institute of Navigation San Diego,California,USA,April 25–27,2006 p883

[9]Zitounia S,Rouabahb K,Chikouchec D,Mokranie K,Atiab S,Harbaf R,Ravierf P 2016 Aerosp.Sci.Technol.50 112

[10]Betz J W,Cahn C R,Dafesh P A,Hegarty C J,Hudnut K W,Jones A J 2006 Proceedings of the 2006 National Technical Meeting of The Institute of Navigation Monterey,CA,USA,January 18–20,2006 p685

[11]Yao Z,Lu M Q,Feng Z M 2010 Sci.China:Phys.Mech.Astron.40 575(in Chinese)[姚铮,陆明泉,冯振明 2010中国科学:物理学力学天文学40 575]

[12]Avila-Rodriguez J A 2008 Ph.D.Dissertation(Munich:University FAF Munich)

[13]Zhang X M,Yao Z,Lu M Q 2011 Sci.China:Phys.Mech.Astron.54 1077

[14]Lestarquit L,Artaud G,Issler J L 2008 Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation Savannah,GA,USA,September 16–19,2008 p961

[15]Tang Z P,Zhou H W,Wei J L,Yan T,Liu Y Q,Ran Y H,Zhou Y L 2011 Sci.China:Phys.Mech.Astron.54 1014

[16]Shivaramaiah N C,Dempster A G,Rizos C 2013 IEEE Trans.Aerosp.Electron.Syst.49 1119

[17]Yao Z,Zhang J Y,Lu M Q 2016 IEEE Trans.Aerosp.Electron.Syst.52 466

[18]Guo F,Yao Z,Lu M Q 2016 GPS Solut.20 1

[19]Martin N,Leblond V,Guillotel G,Heiries V 2003 Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation Portland,OR,USA,September 9–12,2003 p188

[20]Hodgart M S,Blunt P D 2007 Electron.Lett.43 877

[21]Shivaramaiah N C,Dempster A G,Rizos C 2009 Proceedings of the European Navigation Conference on Global Navigation Satellite Systems Citeseer,Braunschweig,Germany,October 19–21,2009 p1

[22]Benedetto F,Giunta G,Lohan E S,Renfors M 2013 IEEE Trans.Veh.Technol.62 1350

[23]Yao Z,Cui X W,Lu M Q,Feng Z M 2010 IEEE Trans.Aerosp.Electron.Syst.46 1782

[24]Yan T,Wei J,Tang Z P,Qu B,Zhou Z H 2015 Wireless Pers.Commun.84 2835

[25]Yan T,Wei J L,Tang Z P 2015 GPS Solut.19 623

[26]Lohan ES 2010 Proceedings of the Institute of Navigation Indian Wells,USA,May 4–6,2010 p245

[27]Macchi F,Petovello M G,Lachapelle G 2008 Proceedings of the Institute of Navigation Savannah,GA,USA,September 16–19,2008 p982

[28]Betz J W,Kolodziejski K R 2009 IEEE Trans.Aerosp.Electron.Syst.45 1538

[29]Betz J W,Kolodziejski K R 2009 IEEE Trans.Aerosp.Electron.Syst.45 1551

[30]Yao Z,Lu M Q 2011 Electron.Lett.47 878

[31]Brian M S,Liu N,Xu Z Y 2010 IEEE Trans.Signal Process.58 2729

[32]Dan C,Moshe Z,Jacob Z 1975 IEEE Trans.Inform.Theory 21 90

PACS:91.10.Fc,84.40.Ua,89.70.–aDOI:10.7498/aps.66.129101

Universal evaluation criteria for code delay estimation error of satellite navigation signals∗

Liu Zhen1)†Zhang Jia-Yi2)Lu Ming-Quan2)Huang Jie1)Zhao Yong-Jun1)

1)(School of Navigation and Aerospace Target Engineering,Information Engineering University,Zhengzhou 450001,China)
2)(Department of Electronic Engineering,Tsinghua University,Beijing 100084,China)

13 March 2017;revised manuscript

6 April 2017)

With the system upgrading and construction demand for new generation global navigation satellite system(GNSS),the navigation signal modulation and multiplexing technology have made great progress.Up to now,many modulation modes for single signal component and many constant-envelope multiplexing methods for multiple signal components have been proposed,meanwhile the new signal structure continues to be presented.The satellite navigation signal code delay estimation error is the most critical factor that determines system service performance.Therefore,it is urgent to give an overall performance evaluation on code delay estimation error of GNSS signals with di ff erent modulation and multiplexing modes,and consequently provide a crucial selection basis for subsequent system application.The code delay estimation error is related to not only signal structure,but also receiver’s receiving model and processing method of code tracking loop.The receiving models of new generation navigation receivers can be classi fi ed as two types.One is matched receiving model which means that the reference signal is the same as receiving signal,and the other is unmatched receiving model,where the reference signal is not the same as receiving signal.Recently,the unmatched receiving model has been extensively applied to the processing of binary o ff set carrier class signals.

Therefore,in this paper we propose an integrated evaluation method for code delay estimation error of navigation signals.Firstly,the equivalent model for the code tracking loop of navigation receivers is generalized and the current navigation receivers are classi fi ed as four types based on whether matched receiving or coherent processing is used.Because the code delay estimation error is dependent on the type,it is necessary to provide an evaluation method for each type.Then,on the assumed condition that the code delay estimation error is very small,the expressions of code delay estimation error for coherent processing and non-coherent processing under matched receiving model are respectively presented and the relationships between each other are discussed under various noise environments and the code loop interval going to zero.The expression of code delay estimation error for non-coherent processing under unmatched receiving model is derived and the relationship with coherent processing is discussed under the same condition as matched receiving model.Finally,the Ziv-Zakai bound of code delay estimation error is derived,which provides a perfect evaluation method when the code delay estimation error is not very small.The proposed method is expressed by power spectrum density of navigation signals,which provides important theoretical guidance for signal design and receiver development,and simultaneously brings great convenience to the evaluation of the signal.Simulation experiment attests to e ff ective evaluation on the code delay estimation error of new generation typical navigation signals.

satellite navigation signals,code delay estimation error,evaluation criteria

10.7498/aps.66.129101

∗国家自然科学基金(批准号:D040103)资助的课题.

†通信作者.E-mail:liuzheninformation@163.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.D040103).

†Corresponding author.E-mail:liuzheninformation@163.com