自适应非凸稀疏正则化下自适应光学系统加性噪声的去除∗

张艳艳 陈苏婷 葛俊祥 万发雨 梅永 周晓彦

(南京信息工程大学,江苏省气象探测与信息处理重点实验室,江苏省气象传感网技术工程中心,江苏省大气环境与装备技术协同创新中心,南京 210044)

自适应非凸稀疏正则化下自适应光学系统加性噪声的去除∗

张艳艳†陈苏婷 葛俊祥 万发雨 梅永 周晓彦

(南京信息工程大学,江苏省气象探测与信息处理重点实验室,江苏省气象传感网技术工程中心,江苏省大气环境与装备技术协同创新中心,南京 210044)

(2017年1月23日收到;2017年3月29日收到修改稿)

自适应光学系统可以实时测量并校正波前信息,但是系统中大量的噪声严重影响了系统的探测精度.自适应光学系统中一般为加性噪声,本文提出一种全新的变分处理模型去除加性噪声,该模型采用自适应非凸正则项.非凸正则项在保持图像细节上较凸正则项具有更好的效果,能更好地保持点源目标的完整性.另外,根据不同区域的噪声水平自适应地构建正则化参数,使不同区域的像素点受到不同程度的噪声抑制,可以更好地保持目标的边缘细节.在算法实现上,为了解决非凸正则项收敛性较差的缺陷,采用分裂Bregman算法及增广拉格朗日对偶算法进行计算.实验及数值仿真结果都表明,该方法能够较好地去除系统中的加性噪声,且光斑信号保存得较为完整,处理后的质心探测精度及信噪比较高.

自适应光学,加性噪声,自适应正则化,非凸

1 引 言

自适应光学(adaptive optics,AO)系统通过实时测量[1−3]、校正受到大气湍流扰动影响的光波前来提高成像系统的成像质量[4,5],在天文观测等领域具有重要的应用.AO系统的噪声为加性噪声,其噪声模型为[6]

其中uk是观测图像,fk是待恢复图像,nk是噪声.对于AO系统而言,nk最主要的来源是背景噪声、电荷耦合器件(CCD)的读出噪声等,其中的背景噪声整靶面分布均匀,较为容易处理[6].读出噪声的分布符合均值为零、方差为σ2的高斯形式,是AO系统中最主要的噪声源,本文只对读出噪声进行分析.

文献[7]提出采用减阈值的方法去除AO系统的加性噪声,并论证了最优阈值的存在.Arines和Ares[8]提出使用最小方差的阈值计算方法.另外,Thomas[9]提出了使用加窗一阶矩的算法来计算质心,加窗法可以有效地降低窗口以外的噪声对质心探测精度的影响,通过适当改变探测窗口面积大小来降低远离光斑质心位置的像素的影响,以提高质心探测精度.但是窗口的尺寸并不能一味地减小,当光斑像素点不能全部在计算窗口内时,误差将增大,因此在利用加窗法进行质心计算时,窗口尺寸的选取至关重要.Baker和Moallem[10]提出了加权一阶矩算法,该算法利用的是光斑信号的高斯形态分布以及光斑信号的灰度值与噪声信号灰度值的差别,光斑信号的灰度值要高于噪声的灰度值,若将整幅图像乘以一个在光斑质心位置处高斯分布的函数,则相当于对光斑图像进行了非线性的增强.

对于去除加性噪声,Rudin等[11]提出了著名的基于全变差的噪声模型.随后又有学者提出了热扩散方程,并在此基础上提出了一系列的改进方法,其中最为广泛使用的是Tikhonov正则项.Tikhonov正则项是平滑的凸正则项,对于保持图像的细节效果不好.随后又有学者提出了非凸正则化模型,实验表明非凸的正则项在保持图像细节上较凸正则项具有更好的效果[11−15].但是,非凸正则项却带来一个问题,就是计算的复杂度.另外,全变差模型的正则化参数通常为常量,这使得位于不同区域的像素点受到的噪声抑制程度相同,导致同质区域的光滑程度不够,或者边缘、纹理区域过度光滑,从而影响噪声抑制效果[16].

基于以上分析,本文提出一种新的非凸正则项的加性噪声去除模型,该模型能够自适应调整正则化参数,在去噪的同时能够较好地保持AO系统的点源目标图像,提高系统的质心探测精度.数值及实验结果表明新模型能够更好地去除点源目标噪声,提高质心探测精度.

2 非凸正则项模型分析

从噪声图中恢复出目标图像信号f的问题可转化为以下问题的求解[17],

其中,∥a∥0表示向量a的L0范数,即向量a的非零元素个数;元素gk做归一化处理后即为原子;ak为各项原子对应分解系数.此时f的求解问题转化为

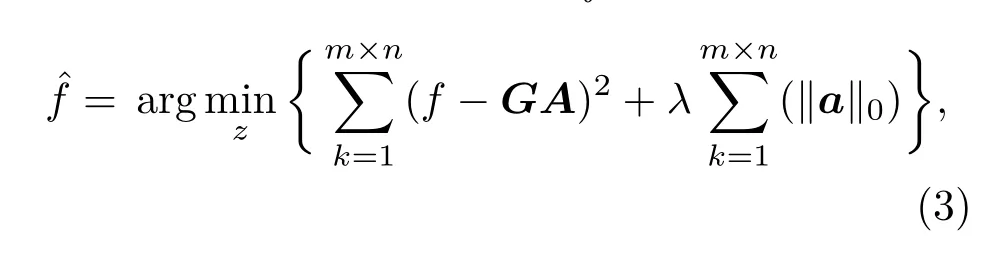
(3)式中L0范数的非凸性,使(3)式的求解变成了NP难的组合优化问题.最初,Mallat和Zhang[18]通过迭代的贪婪算法(匹配追踪算法)来求解;随后,Donoho和Tsaig[19,20]用L1范数取代L0范数,将(3)式转换成(4)式进行优化求解,

在(4)式中,正则化参数λ的大小决定噪声抑制的程度,对于同质区域,λ的取值应该偏大,但是较大的λ会使得噪声抑制过度,从而造成边缘、纹理细节信息的丢失;而对于边缘、纹理细节区域,会造成同质区域噪声的抑制不足.不管是(3)式还是(4)式,其中λ的取值都是固定的,但是这对于保持图像的细节而言并不是最好的选择,尤其对于AO图像,由于点源目标较小,图像细节不清晰,固定的λ值使得去噪之后的光斑的失真度更高,质心精度降低.因此,有必要选择可以自适应调整的参数.

文献[16]提出了采用变分模型解决以上问题,并采用λi替换λ的方法进行自适应的参数选取,本文基于此思路提出了适用于AO系统点源目标的提取方法.文献[16]利用最大后验概率估计得到相应的最小化问题,将(4)式转化为

式中ϕ(·)为正则化函数,

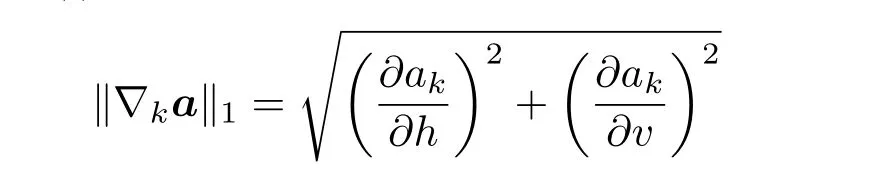
表示系数ak的梯度,其中分别代表水平和垂直方向的偏导.文献[16]提出将其中的ϕ∥∇ka∥1项替换成一个关于∇ka的函数,

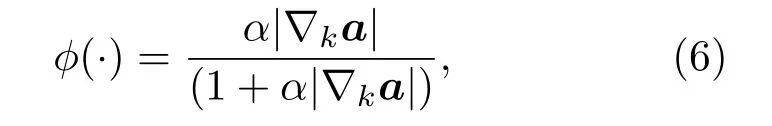
其中α是一个足够大的辅助常数.则λk的Euler-Lagrange方程为

上述方法可以自适应选取正则化参数,具有较好的效果,但是由于光学点源目标较小,细节较少,直接采用(7)式约束效果较差.因此本文针对此类点源目标提出了一种新的定义方法,

此模型与(6)式相比,对于|∇ka|进行偏导处理.(6)和(8)式的比较如图1所示,其中为了简便起见,引入新的变量s,并令s=|∇ka|.从图1可以看出,在s<1时,(8)式的取值较(6)式略小,但是在s>1时,(8)式的取值较(6)式具有明显的增大,而s<1时对应于点源目标图像的目标与噪声的梯度较大,这也说明该正则项能够更好地保持光斑图像的完整度,提高质心探测精度.

所提出正则项具有以下特点.

1)此正则项参数在稀疏领域具有优势.事实上,我们所提出的正则项可以看作是a的梯度模量的稀疏测量.其中相当于梯度模量a的L1范数,而我们提出的非凸正则项可以看做的L0范数,此时的β需要设置的较大.而L0较L1范数具有更大的稀疏性,因此其能够更好地进行稀释分解及保存点源目标的边缘.

2)此正则项可以防止图像的过平滑.为了防止边缘的过平滑,ϕ(·)应该呈现增长的趋势,但其终值(其中c是常数),使得正则项的作用不会影响到a的梯度,我们所提出的算法满足此要求.

图1 正则项ϕ(s)=s/(1+s)和ϕ(s)=s2/(1+s2)的比较Fig.1.The comparison of two nonconvex regularization function ϕ(s)=s/(1+s)and ϕ(s)=s2/(1+s2).

3)本文的正则项是非凸项,虽然非凸项收敛性较差,但是非凸正则化参数对于图像的微小变化更为敏感,可以更好地保持图像边缘的细节信息,对于本身细节就较少的AO点源目标来说具有更好的提取效果.

3 解决方法

尽管新正则项在图像的保边方面具有一定优势,但由于它的非凸性,模型(5)很难采用经典的算法直接进行求解,本文采用分裂Bregman算法[21]及增广拉格朗日对偶算法[22]相结合的方法进行求解.

首先引入辅助变量v∈Rr,将无约束的极小化模型(5)转化为如下含有约束的极小化模型:

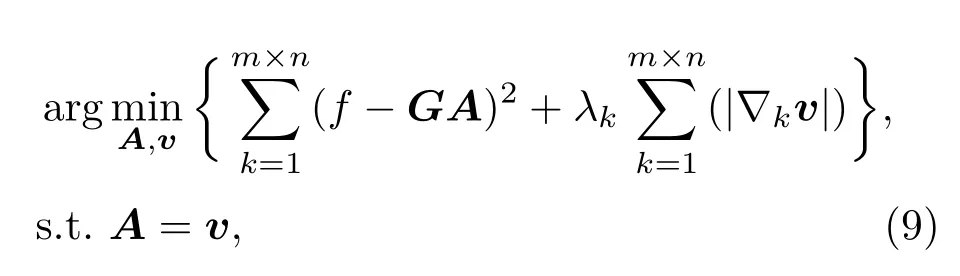
求解(9)式的分裂Bregman算法的步骤如下:

1)选取图像,给定参数初始值µ>0,λk>0,选择Global字典,并令迭代指标i=1;

2)求解(a(i),v(i)),

3)根据极小化问题(10)的解,更新ri:

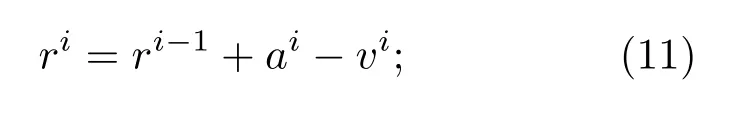
4)更新i=i+1,当步骤2和3收敛时,输出a(i),v(i);否则,返回步骤2;

5)采用交替迭代的方法进行求解a(i)和v(i),即求解如下的两个公式,

4 数值处理结果及分析

4.1 仿真结果

为便于参数的调节,我们模拟了含有不同噪声水平的光斑图像,模拟条件如下:图像大小为201 pixels×201 pixels,光斑中心(x0,y0)坐标为(100,100),峰值50 ADU,等效高斯宽度为σA=1.25 pixels.此条件下模拟出的目标光斑在5×5像元内集中了80%以上的能量.

在实验中,我们发现对去噪效果影响较大的参数是β,此参数不仅依赖于噪声的强度,而且图像本身对其影响也较大.在去噪过程中,此参数对点源图像的复原精度及细节保留程度均有较大的影响,但是如何有效调节参数β使得去噪效果达到最佳,是本文下一步的研究方向.根据多次实验测试,本文中β的取值在[0,5]之间.

我们分别将测试图像加上不同强度的高斯噪声,噪声强度主要体现在其方差σ上,σ的取值较小意味着噪声的强度较弱[23−25],本文σ取值为[1,8].比较了所提出算法模型及减阈值算法的峰值信噪比(PSNR)及质心探测精度,PSNR的定义式为

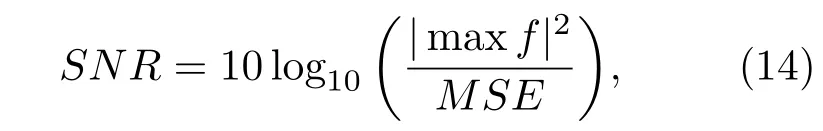
式中maxf表示真实图像f的最大值,MSE表示为

质心探测精度采用质心偏差的平均偏差的均方根值(RMS)及峰谷值(PV),其中质心偏差的PV表示其偏差的峰谷值,RMS表示质心偏差的起伏.

对光斑图像添加不同水平的噪声,如图2所示,可以看出随着σ的增大,光斑信号被噪声所淹没.图3是采用减阈值算法后的光斑图像,可以看出在σ较小时,采用减阈值算法效果较好,但是随着σ值的增大、图像噪声的增强,减阈值算法对噪声的滤除效果较差.图4是采用(6)式进行处理后的效果,可以看出在信噪比较低的情况下,该算法较减阈值算法对噪声的处理能力具有明显的优势,但是,该算法对光斑的完整性保持不好,从而会影响质心探测的精度.图5是采用本文算法处理后的效果,可以看出在保持良好的去噪性能的基础上,本文算法能够较好地保持光斑的边缘,使光斑信号更加完整.

图2 含有不同噪声水平的的光斑图像Fig.2.The spots under di ff erent noise levels.

图3 减阈值算法处理后的效果Fig.3.The spots obtained by using threshold reduction algorithm.

图4 采用(6)式作为正则项处理后的结果Fig.4. The processing results obtained by using Eq.(6)as a adaptively regularization term.

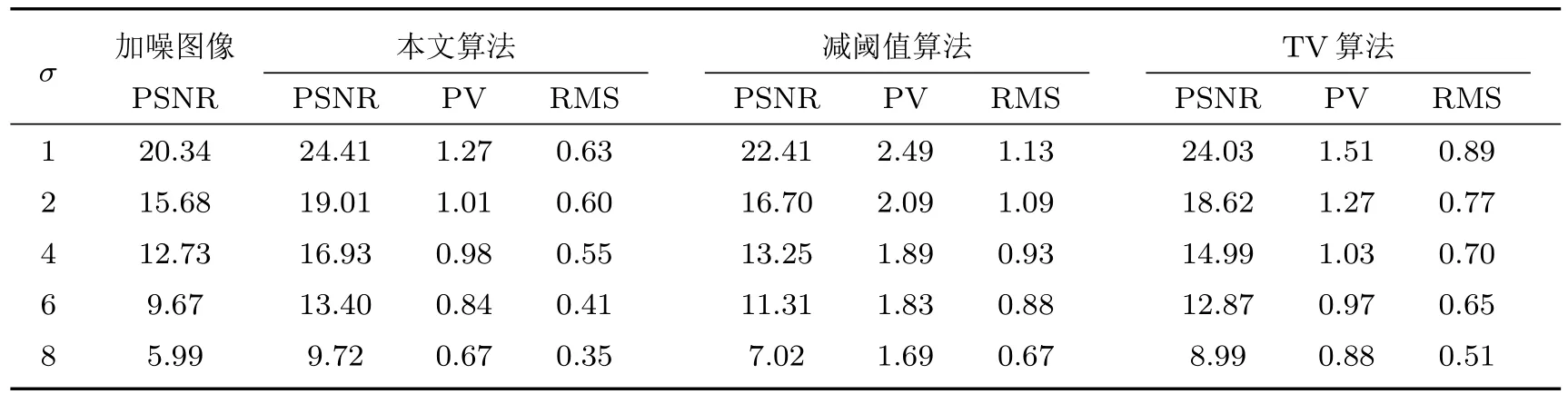
表1 不同噪声水平下各算法处理后质心偏差RMS,PV及PSNR比较Table 1.The comparison of centroid deviation’s RMS,PV and PSNR under di ff erent noise levels for three processing methods.

图5 本文提出算法处理效果Fig.5.The processing obtained by results using our proposed model.

图6 (a)较小子孔径时含有噪声的光斑图像;(b)减阈值效果图;(c)采用(6)式处理后的效果图;(d)本文算法处理后的效果图Fig.6.(a)Small size sub-aperture image with noise;(b)the image after subtracting the threshold;(c)the processing results obtained by using Eq.(6)as a adaptively regularization term;(d)the image after processed by the proposed method.

一般地基光电望远镜AO系统,子孔径及光斑都较小,本文对此情况下的处理效果进行了仿真分析.仿真参数:子孔径大小为10 pixels×10 pixels,峰值50 ADU,艾里斑集中在2×2像素内,此模拟子孔径图像的信噪比约为14 dB.从图6可以看出,虽然处理效果较大尺寸子孔径图像略有下降,但其去除噪声的效果要好于减阈值算法,另外,在光斑的边缘细节处理上要明显好于(6)式的处理结果.

为了进一步验证本文算法的有效性,对比分析了处理前后的质心偏差,如图7所示.从图7可以看出,三种算法处理后的质心偏差都随着噪声强度的增加而增大,但可以较为明显地看出本文算法的优势.另外,比较表1中处理前后的PSNR及质心探测精度可以看出,本文所提出的模型与减阈值算法及文献[16]算法相比能够获得更高的PSNR及更低的质心探测误差.

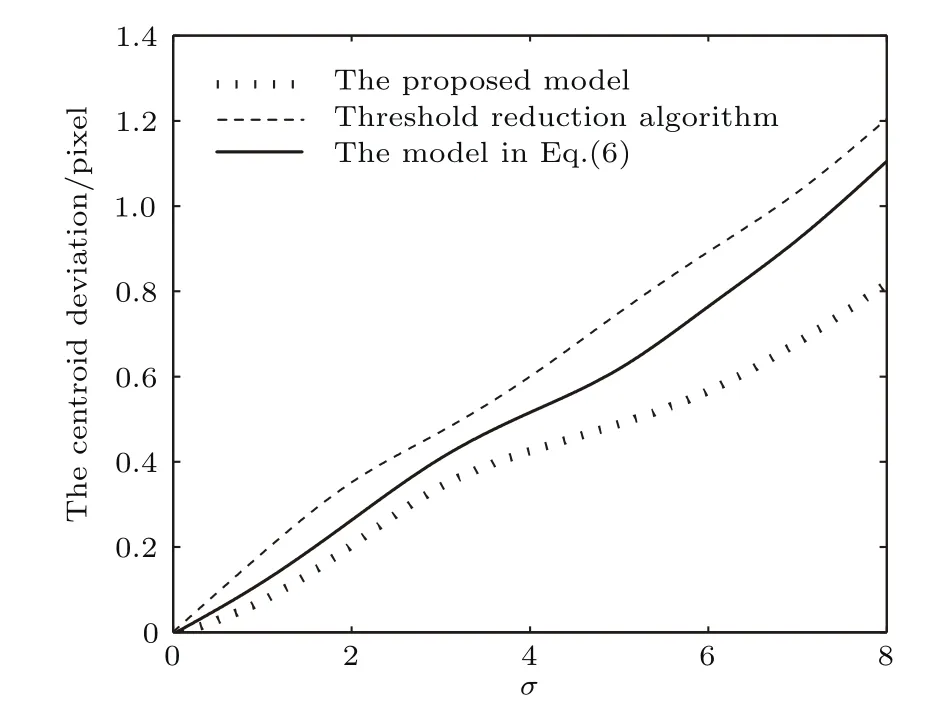
图7 不同噪声水平下各算法处理后的质心偏差图Fig.7. The centroid deviation comparison among these three methods.

4.2 实验结果与分析

为了验证本文算法的有效性,另选择夏克-哈特曼图像进行实验,并将几种算法处理的效果进行了比较,如图8所示.实验中,光斑大小为6 pixel×6 pixel,CCD靶面为(768×484)pixels,子孔径大小为(20×20)pixels,有效子孔径数400,每一个子孔径为一个0.51 mm的方孔.图8(a)是所采集到的含有较强噪声的图像,信噪比约为18 dB.图8(b)是减阈值处理的效果图,此时所选取的阈值大小为最优阈值的估计值,约为27 ADU,可以看出经过减阈值处理后仍有较强的噪声残留,处理后的信噪比约为25 dB,略有提高.图8(c)是采用(6)式作为自适应正则项处理后的结果,处理后的信噪比约为26.5 dB,较减阈值算法稍有提高.图8(d)是采用本文提出的方法处理后的结果,可以看出个子孔径光斑提取效果较好,且天光背景噪声滤除较为干净,此时信噪比约为32.7 dB.

图8 (a)含有较强天光背景的夏克-哈特曼图像;(b)减阈值效果图;(c)采用(6)式处理后的效果图;(d)本文算法处理后的效果图Fig.8.(a)Shack-Hartmann image with high background;(b)the image after subtracting the threshold;(c)the processing results by using Eq.(6)as a adaptively regularization term;(d)the image processed by the proposed method.

图9是选取上述哈特曼的单个子孔径图像进行处理前后的对比分析,从图中可以看出,处理前天光背景较强,光斑被背景及噪声淹没,减阈值算法处理后噪声起伏仍较大,采用本文算法处理后,光斑目标提取较好.由此可以看出,在信噪比较低时,本文算法较减阈值算法仍然有较大的优势.

在信号较弱即信噪比更低时对上述算法的处理效果进行对比分析,为方便起见,选取了部分子孔径进行结果演示,如图10所示.从图10可以看出,由于光斑信号较弱,几乎被噪声所淹没,此时信噪比约为12 dB.减阈值算法处理后噪声起伏仍较大,光斑提取效果较差,处理后信噪比约为13.5 dB,稍有提高.图10(c)是采用(6)式处理后的结果,可见仍有大量噪声残留,且目标光斑不完整,处理后的信噪比约为19.5 dB.图10(d)是采用本文方法处理后的结果,可以看出由于原光斑较弱,处理后仍有一定的噪声残留,此时信噪比约为25 dB,且光斑保留较图10(c)更为完整.

图9 (a)含有噪声的单个子孔径图像;(b)减阈值处理后效果图;(c)采用(6)式处理后的效果图;(d)本文算法处理后的效果图Fig.9.(a)Sub-aperture image before being processed;(b)the image after subtracting the threshold;(c)the processing results by using Eq.(6)as a adaptively regularization term;(d)the image processed by the proposed method.

5 结 论

本文提出了一种新的去除AO系统加性噪声的方法,该方法考虑到点源目标特性,采用非凸正则项在稀疏域进行处理,能够更好地保持点源目标.对该方法的优势进行了详细的讨论.为了克服非凸正则项收敛性差的特点,本文采用分裂Bregman算法及增广拉格朗日对偶算法对该模型进行计算.仿真及实验结果表明,本文所提出的非凸正则化模型能够较好地去除噪声,提高点源光斑目标的质心探测精度.

图10 (a),(b)光斑较弱时低信噪比的夏克-哈特曼及单个子孔径图像;(c),(d)减阈值效果图及单个子孔径图像;(e),(f)采用(6)式处理后的效果图及单个子孔径图像;(g),(h)本文算法处理后的效果图及单个子孔径图像Fig.10.(a)Shack-Hartmann image with weak signal in low signal-to-noise ratio and(b)the corresponding subaperture image;(c)the image after subtracting the threshold and(d)the corresponding sub-aperture image;(e)the processing results by using Eq.(6)as a adaptively regularization term and(f)the corresponding sub-aperture image;(g)the image processed by the proposed method and(h)the corresponding sub-aperture image.

[1]Roberto R,Enrico M,Gianpaolo V 2000 Nature 403 54

[2]Law N M,Morton T,Baranec C,Riddle R,Ravichandran G,Ziegler C,Das H K 2014 Astrophys.J.791 35

[3]Adams E R,Dupree A K,Kulesa C,McCarthy D 2013 Astron.J.146 71

[4]Li C H,Xian H,Rao C H,Jiang W H 2006 Opt.Lett.31 2821

[5]Li C H,Xian H,Jiang W H,Rao C H 2007 Appl.Phys.B 88 367

[6]Shen F,Jiang W H 2000 Acta Opt.Sin.20 666(in Chinese)[沈锋,姜文汉 2000光学学报 20 666]

[7]Ma X Y,Rao C H,Zheng H Q 2009 Opt.Express 17 8525

[8]Arines J,Ares J 2002 Opt.Lett.27 497

[9]Thomas S 2004 Proc.SPIE 5490 1238

[10]Baker K L,Moallem M M 2007 Opt.Express 15 5147

[11]Rudin L I,Osher S,Fatemi E 1992 Physica D 60 1

[12]Strong D M,Chan T F 1996 Spatially and Scale Adaptive Total Variation Based Regularization and Anisotropic Di ff usion in Image Processing Diusion in Image Processing,UCLA Math Department CAM Report

[13]Ramani S,Blu T,Unser M 2008 IEEE Trans.Image Process.17 1540

[14]Lin Y,Wohlberg B,Guo H 2010 Signal Process.90 2546

[15]Aubert G,Aujol J 2008 Siam.J.Appl.Math.68 925

[16]Han Y,Feng X C,Baciu G,Wang W W 2013 Pattern Recogn.46 989

[17]Alliney S,Ruzinsky S A 1994 IEEE Trans.Signal Process.42 618

[18]Mallat S M,Zhang Z F 1993 IEEE Trans.Signal Process.41 3397

[19]Donoho D 2006 IEEE Trans.Inform.Theory 52 1289

[20]Donoho D,Tsaig Y 2006 Signal Process.86 533

[21]Goldstein T,Osher S 2009 Siam.J.Imag.Sci.2 323

[22]Tai X C,Wu C 2009 Scale Space and Variational Methods in Computer Vision Norway,June 1–5,2009 p502

[23]Gang P,Zeng H,Xuan L 2008 Chin.Phys.Lett.25 989

[24]Zhu Z Y,Da Y L,Li F H,Quan Q M,Cheng L Y,Zhao L C,Li X 2016 Chin.Phys.B 25 090702

[25]Cheng S Y,Liu W J,Chen S Q,Dong L Z,Yang P,Xu B 2015 Chin.Phys.B 24 084214

PACS:95.75.Qr,42.68.–w,07.05.PjDOI:10.7498/aps.66.129501

Removal of additive noise in adaptive optics system based on adaptive nonconvex sparse regularization∗

Zhang Yan-Yan†Chen Su-Ting Ge Jun-Xiang Wan Fa-Yu Mei Yong Zhou Xiao-Yan

(Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology,Jiangsu Technology and Engineering Center of Meteorological Sensor Network,Jiangsu Key Laboratory of Meteorological Observation and Information
Processing,Nanjing University of Information and Science Technology,Nanjing 210044,China)

23 January 2017;revised manuscript

29 March 2017)

Adaptive optics(AO)system which is widely used in astronomical observations can improve the image quality by the real-time measurement and correction of the wave-front.One of the main problems in the AO system is the poor quality of the image because of the system noises.The noises in AO system are additive noises.The main sources of the noises are the background noise,the photon noise,and the readout noise of charge-coupled device.The background noise is distributed evenly and is easy to process.The photon noise is dependent on the characteristics of the spot itself.Readout noise,which is Gaussian distribution with the mean value of 0 and the variance of σ2,is the main noise source in AO system.In this paper,we focus on the readout noise and propose a new regularization model to remove additive noises from the AO system.In this model,the regularization parameters can be adaptively changed.A nonconvex regularization term is used to make the homogeneous region of the image smooth efficiently,while the integrity of the spot can be well restored.The properties of the regularization proposed are shown below.1)The proposed nonconvex regularization term can act as the L0norm which is sparser than L1norm.2)The proposed model can protect the edge of the spot from over smoothing.To prevent the edges from over smoothing,the regularization parameter must be an increasing function.Moreover,it converges to a constant so that it cannot a ff ect the strong gradient of the image.3)The regularization term proposed is nonconvex which is more sensible to the minor change of the image.Therefore,the edges of the image can be better preserved.Though the proposed model can well preserve the edges of the spot,it is difficult to resolve by traditional methods because of the nonconvexity.Split Bregman algorithm and augmented Lagrangian duality algorithm are used to solve this problem.We can obtain a denoised spot image as well as an edge indicator by using the proposed model.The visual and quantitative evaluations are used to value the restored images.The evaluating indicators are the peak signal-to-noise ratio and centroid detecting error which includes the root mean square and the peak valley value of the centroid deviation.The simulation and experimental results show the efficiency of this model in removing the additive noises from the AO system.

adaptive optics,additive noise,adaptively regularization term,nonconvex

10.7498/aps.66.129501

∗国家自然科学基金(批准号:61071164)、江苏省高校自然科学研究基金重大项目(批准号:12KJA510001)、江苏省气象探测与信息处理重点实验室项目(批准号:KDXS1405)、江苏省2016大学生实践创新计划(批准号:201610300254)、江苏高校优势学科II期建设工程和江苏省双创计划资助的课题.

†通信作者.E-mail:002243@nuist.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Nature Science Foundation of China(Grant No.61071164),the Major Project of Nature Science Foundation of Higher Education Institution of Jiangsu Province,China(Grant No.12KJA510001),the Program of Jiangsu Key Laboratory of Meteorological Observation and Information Processing,China(Grant No.KDXS1405),the Jiangsu Province College Students Practice and Innovation Training Platform,China(Grant No.201610300254),the Priority Academic Program Development of Jiangsu Higher Education Institutions,China,and the Jiangsu Innovation and Entrepreneurship Group Talents Plan,China.

†Corresponding author.E-mail:002243@nuist.edu.cn