同轴结构中压力波法测量空间电荷分布的物理模型研究∗

孙雅丽 张冶文†Stephane Hole2) 马朋 郭聪郑飞虎 安振连

1)(同济大学电气工程系,上海 201804)

2)(ESPCI-ParisTech,Paris 75005)

3)(同济大学,上海市特殊人工微结构材料与技术重点实验室,上海 200092)

同轴结构中压力波法测量空间电荷分布的物理模型研究∗

孙雅丽1)张冶文1)3)†Stephane Hole1)2)马朋3)郭聪1)郑飞虎1)安振连1)

1)(同济大学电气工程系,上海 201804)

2)(ESPCI-ParisTech,Paris 75005)

3)(同济大学,上海市特殊人工微结构材料与技术重点实验室,上海 200092)

(2016年12月15日收到;2017年4月7日收到修改稿)

从压力波法测量平板样本中空间电荷分布的理论分析出发,提出了对于同轴结构的固体电介质中空间电荷分布的压力波法测量的物理模型,并得出了测量电流的解析的数学表达式.依据泊松方程,考虑样品内的电场强度、介电常数和空间电荷密度随外界声波扰动而发生变化,将圆柱试样受到的压力波的影响分解成样品形变和质点位移两部分,进而得到了以同轴结构中空间电荷分布的压力波法测量的电压与电流表达式.测量电流的数学表达式表明,对于同轴结构,压力波法的测量电流信号不像平板结构中那样基本正比于空间电荷分布,而是应该做进一步的修正处理.

空间电荷分布,压力波法,固体电介质,同轴结构

1 引 言

固体电介质中的空间电荷测量方法与技术在近30年中取得了巨大进步,目前国际上普遍认可空间电荷对绝缘材料的电特性有明显的影响[1],因此使得固体电介质空间电荷研究成为研究热点问题之一.空间电荷测量技术是空间电荷研究的基础,绝缘电介质中空间电荷分布测量技术的不断进步使得空间电荷研究不断取得成果.20世纪80年代之前出现了有损的测量技术,80年代出现了多种无损测量技术,而在90年代之后趋于成熟,开始应用到绝缘材料的研究中[2].

现在已经有很多种空间电荷的测量方法:1976年,Collins[3]提出了热脉冲法;同年,Laurenceau等[4,5]提出压力脉冲法;在此基础上实现了激光诱导压力波(laser induced pressure propagation,LIPP)法[6];后来还出现了压电诱导压力波(piezo-electric induced pressure wave propagation,PIPWP)法[7],目前将PIPWP法与LIPP法统称PWP法,即压力波法;而Lang和Das-Gupta[8]在热脉冲法的基础上共同提出了激光光强调制法.与压力波法基本平行的还有一种比较成熟的测量方法是电声脉冲(pulsed electro-acoustic,PEA)法[9].目前,在对于绝缘材料的空间电荷特性研究中,PWP法和PEA法是比较常用的两种测量方法[10].

以上这些测量方法的物理模型都是基于平板电介质结构,所得到的空间电荷分布也都是针对平板在深度方向上的空间分布.对于平板结构,由于其波传播规律比较简单,物理模型也比较清楚,因此现在已经有了规范的测量技术[11,12].而对于同轴结构,例如在同轴的电力电缆中,以及在中心导体为金属细丝的高度不均匀电场的结构中,目前的空间电荷测量方法的理论分析是不完全适用的.有的作者用近似的处理方法,直接用平板试样对实验数据进行修正,用纵向深度比例调整的方法解决同轴结构中的空间电荷测量问题[13,14].只是一种非常粗糙的近似处理方法,缺乏清楚可信的理论分析基础,没有明确的物理模型,不能从原理上解决问题.因此很有必要对压力波法测量同轴结构的固体电介质中空间电荷分布建立一个清楚可信的物理模型,从而进行严格的数学分析,得到压力波传播法对于同轴结构中空间电荷分布测量的解析表达式.

本文重点介绍压力波法在同轴结构的固体电介质中空间电荷分布测量的理论模型,其物理模型以同轴结构的波动方程与同轴的压力波向内传播的波动方程及其解为基础,考虑样品内电场强度、介电常数和空间电荷密度随外界声波扰动而发生变化,将圆柱试样受到的压力波影响分解成样品形变和质点位移两部分,进而得到同轴结构的固体电介质中空间电荷分布测量的电流解析表达式.

2 同心圆柱试样中压力波法测量的物理模型

在激光压力波法中,激光照在靶上就会生成压力波.当扰动的弹性波在介质中以声速传播时,破坏了介质内部原先的弹性力和电荷产生的电场力的平衡,引起介质中的电荷发生微小位移,电荷的微小位移又导致介质电极上的感应电荷量的变化.因此在外电路上可观测到电流或电压信号的变化,从而获得介质中空间电荷分布的有关信息.

假设均匀介质的内径、外径分别为rB和rA,因此可以得到样品两电极的电位差Um(t)为

其中UB,UA分别为内外径处的电位;E(r,t)为电场强度.当样品内的电荷受到外界声波扰动而失去平衡位置时,泊松方程中的电场强度、介电常数、空间电荷密度均发生变化.如图1所示,只考虑一维情况,当样品内的电荷受到外界声波扰动而失去平衡位置时,电场强度E(r,t)则成为E(r,t)+δE(r,t),介电常数ε变成ε+δε,空间电荷密度ρ(r,t)变成ρ(r,t)+δρ(r,t),并且发生扰动后忽略二次项可得

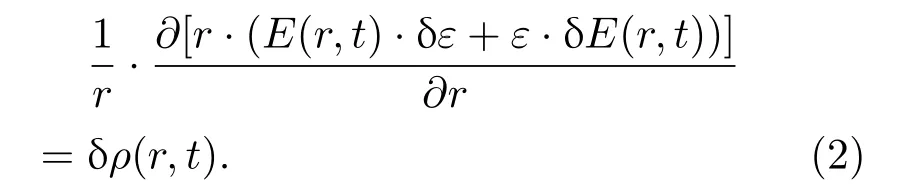
如图2所示的坐标系,假设压力波从样品的右侧开始传播,那么在压力波扰动之前样品内的任意质点a相对于原点的位置为r,样品受到压力波扰动时,样品的介电常数、空间电荷的密度等物理量都将相应地发生变化.我们可将扰动过程分成两个步骤:I)样品只发生形变;II)不考虑形变,仅考虑质点发生位移η(r,t)[15,16].

图1 压力波法测量原理Fig.1.The measurement principle of PWP method.

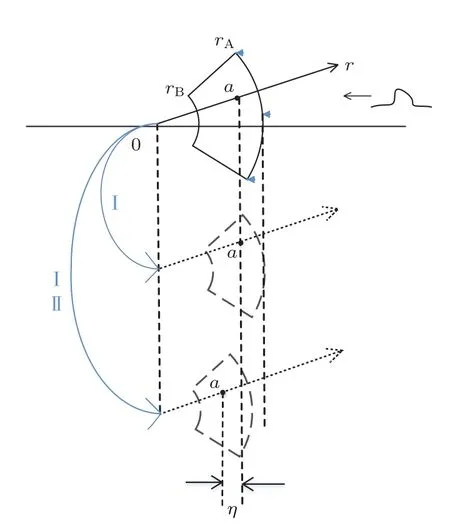
图2 外界扰动对样品作用的示意图Fig.2.In fl uence of the disturbance.

2.1 样品形变的影响

假设样品在受到扰动发生形变后,质点a相对于坐标轴没有位移,如果样品受到扰动以前介电常数为ε,根据材料变化的性质,发生扰动以后样品的r点介电常数增量可表示为[5]

式中ε′为扰动后的介电常数,p(r,t)表示r点处的剖面压强,χ是杨氏模量Y的倒数,A是与材料性质有关的量.在轴对称结构,柱坐标系(r,θ,z)内,若只有内部均布径向载荷作用,则容器的变形可以看作平面应变,即位移η(r,t)不为零,且应变为−∇·η(r,t)[17],故

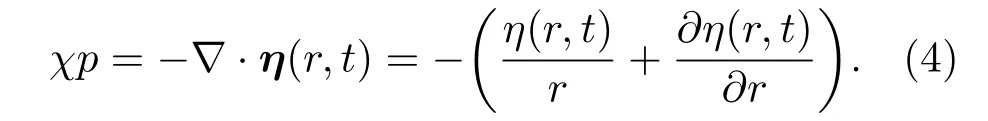
同理,发生扰动后r点的空间电荷密度的增量(δρ)1为

式中ρ′(r,t)为扰动后的介电常数.

2.2 质点位移的影响

将原来的材料视为各向同性的固体样本,故原来介电常数ε可以看作为常数.实际上我们任意选取的质点a在样品发生形变的同时,它相对固定坐标轴上的r点发生了相对微小位移η(r,t),如果只考虑位移,那么对于坐标轴上的r点,由于空间电荷分布的不均匀性,质点位移造成的r点空间电荷密度的增量(δρ)2为

同时考虑I和II两种情况,因此可得

综合考虑介电常数和空间电荷密度的变化并将其代入(2)式进行积分计算可得到样品中两电极的电位差为

图3所示为同轴结构压力波法原理图,假设同轴圆柱试样的电容为C0,由于压力波的作用,空间电荷的运动会产生一定的电流,考虑到上述计算的电位差是两电极之间的电位差,因此外部的测量电流方向应与试样内部电流方向相反,那么根据电流和电压之间的关系可进一步得出圆柱试样的电流方程,

图3 同轴结构压力波法原理图Fig.3.The principle diagram of the coaxial structure in PWP method.

从方程(10)可知电流的变化与压力波和位移相关,但是该方程并不能直接反映压力波与电流之间的关系.因此我们将通过研究圆柱坐标系的波动方程,得出位移和压力波的关系,从而得出与压力波相关的电流方程.在传播过程中,压力波以的速度向中心汇聚[18],故压力波可近似得

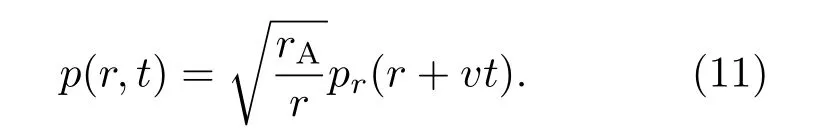
根据已知压力波和位移的关系为

通过傅里叶变换可以得到位移和压力波的关系满足

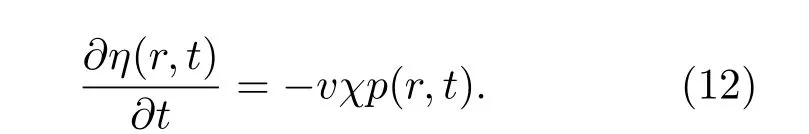
将其代入(10)式可得

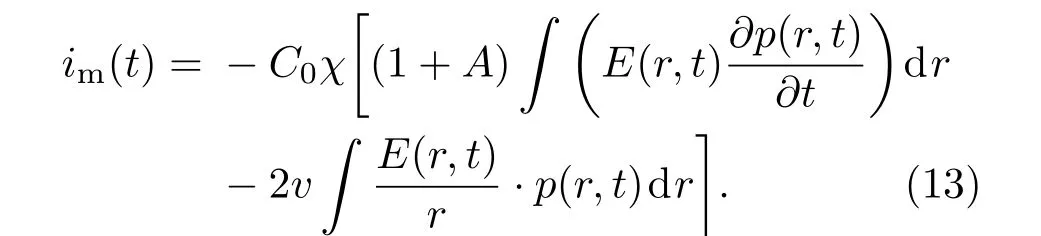
(13)式表示对样品施加压力波前后电极两端的短路电流,并反∫映(了压力波传播)时的变化过程,其中项反映压力波∫在 内外侧电极上空间电荷的瞬时变化,而则反映压力波在圆柱试样的绝缘层中传播的空间电荷变化情况.式中C0为同轴圆柱试样的电容,χ为杨氏模量Y的倒数,A是与材料特性相关的量,v表示压力波在试样中的传播速度,p(r,t)表示任意一点r处的剖面压强,E(r,t)表示任意一点r处的电场强度.

3 测量电流的近似直观表达式

假设压力脉冲p(r,t)沿r轴的负方向以声波v传播,而且在传播过程中无畸变和衰减,其波前位置为r=rA+vt,则满足关系式dr/dt=v.利用

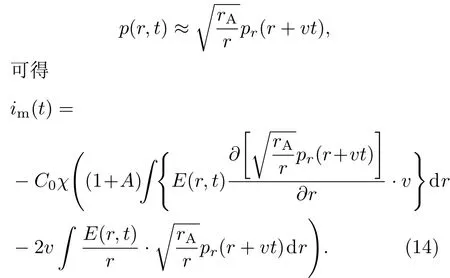
假设压力波为很窄的矩形脉冲波,脉宽为τ,压力为P0的压力波在试样中无衰减和畸变,由外向内传播.其中P0为t=0时,在r=rA处的压力波幅值.且近似认为E(r,t)≈E(r,0),根据泊松方程可以将电流方程简化为

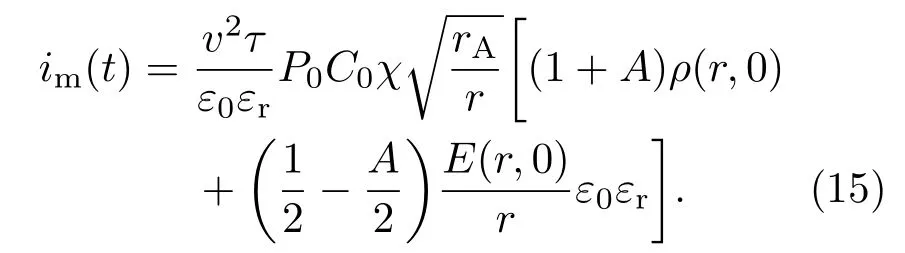
(15)式表明,对于同轴结构的绝缘介质试样,用压力波法可以得到相应的测量电流,可以用(15)式近似表示,其中ρ(r,0)表示压力波传播到任意质点r处的空间电荷密度,在半径不是非常小的情况下,上式中的第二项与场强直接相关,它与(1+A)ρ(r,0)相比明显较小,在很多情况下可以忽略不计.因此基本上可以认为测量电流与空间电荷密度成正相关.但是由于压力波的聚焦作用,越靠近轴心处,电流的幅度越大,因此同轴试样的压力波法电流信号不像平板试样那样正比于空间电荷分布,而是必须进行必要的半径纠正.

4 圆柱形试样的空间电荷实验测量

因无法直接用实验的方法验证以上公式的正确性,故采用与平板试样实验对比的方法进行验证.平板试样的短路电流为[19]

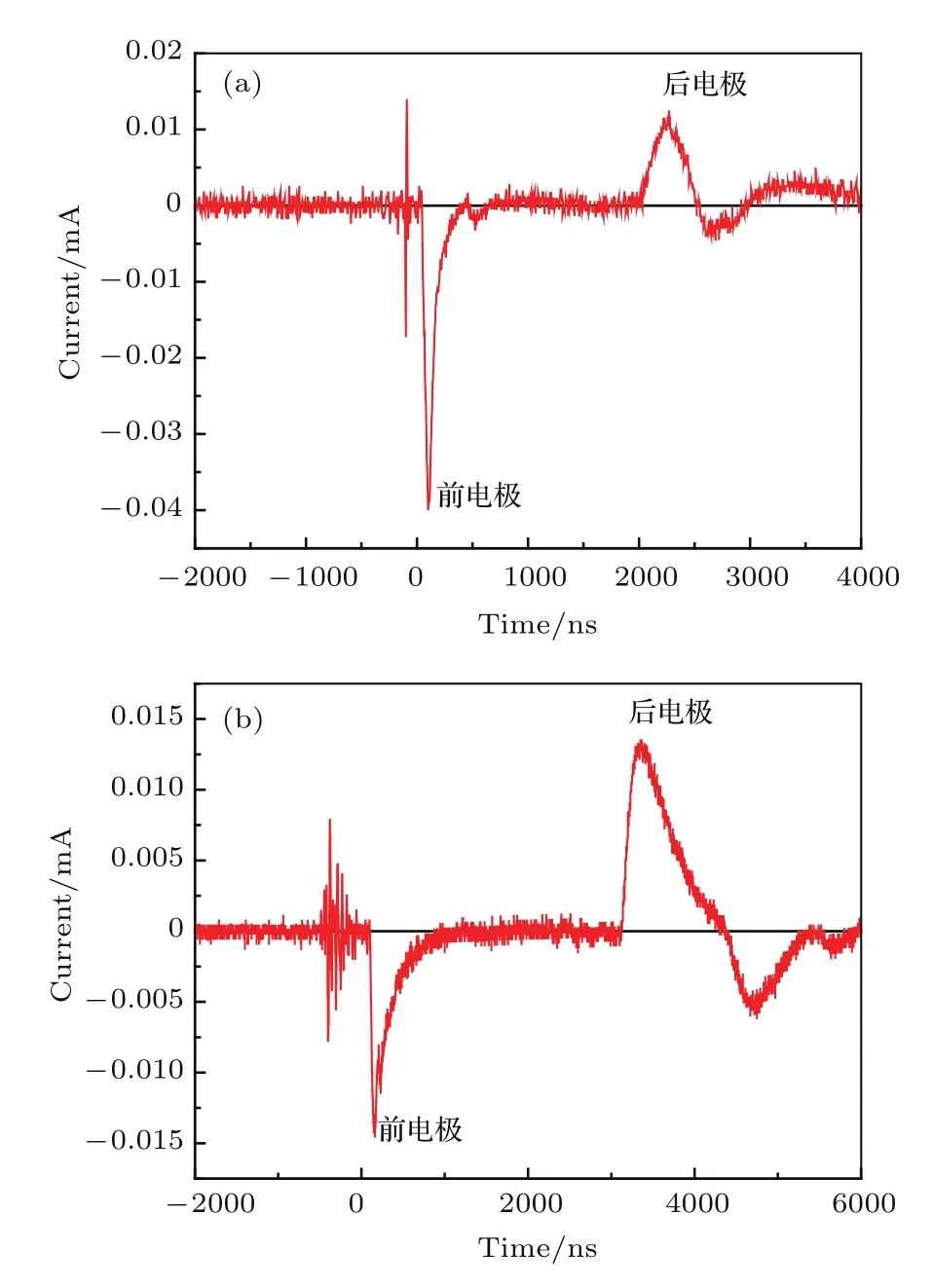
图4 (a)4.5 mm平板样品在−10 kV电压下的测量电流[21];(b)绝缘层厚度为4.5 mm电缆样品在−10 kV电压下的测量电流Fig.4.(a)The induced current signal measured from the planar sample with the thickness of 4.5 mm under the voltage of−10 kV;(b)the induced current signal measured from the cable with thickness of insulating layer of 4.5 mm under the voltage of−10 kV.

由于聚合物样品本身存在一定的压力波色散,因此前电极与后电极的信号幅度不同,而信号的积分面积接近[20].为此,对前电极信号与后电极信号的积分面积进行比较可以分析压力波法信号的有效性.图4(a)所示为4.5 mm平板样品在−10 kV电压下的测量电流信号,此时,压力波在平板样品内传播的过程中产生的出口处电流信号与入口处电流信号的面积比为0.82(理论值应为1).由(16)式可知,压力波传播的过程中,其出口处短路电流应与入口处短路电流相等,而实际上存在压力波的色散与衰减,因此在实际的测量信号中,其出口处电流信号会略小于入口处电流信号.

图4(b)所示为绝缘层厚度为4.5 mm、内导体半径为5 mm、外导体半径为9.5 mm、电缆试样在−10 kV电压下的测量电流信号[20],可知出口处电流信号与入口处电流信号之比为2.23.由(15)式得出口处短路电流与入口处短路电流信号比应为2.62,由此可得实际测量信号约为理论值的0.85倍,与平板试样的0.82基本相同.因此,本文得出的空间电荷表达式(15)是可信的.

5 结 论

本文阐述了同轴圆柱试样中空间电荷分布的测量原理与数据处理方法.与平板试样相比较,激光照在靶上就会生成同心柱面压力波,由于同轴结构的影响,压力声波在向内传播的过程中会产生明显的压力波聚焦效应,从而引起测量信号随着声波的传播逐渐增大.与平板试样相比较,圆柱形试样的空间电荷测量信号的分析理解更为复杂.

[1]Boggs S 2004 IEEE Electr.Insul.Mag.20 22

[2]Lewiner J 2010 IEEE Trans.Dielectr.Electr.Insul.171096

[3]Collins R E 1976 J.Appl.Phys.47 4804

[4]Laurenceau P,Ball J,Dreyfus G,Lewiner J 1976 CR Acad.Sci.Paris 283 135

[5]Laurenceau P,Dreyfus G,Lewiner J 1977 Phys.Rev.Lett.38 46

[6]Sessler G M,West J E,Gerhard G 1982 Phys.Rev.Lett.48 563

[7]Satoh Y,Tanaka Y,Takada T 1997 Electr.Eng.Jpn.121 1

[8]Lang S B,Das-Gupta D K 1986 J.Appl.Phys.59 2151

[9]Li Y,Yasuda M,Takada T 1994 IEEE Trans.Dielectr.Electr.Insul.1 188

[10]Lewiner J,Hole S,Ditchi T 2005 IEEE Trans.Dielectr.Electr.Insul.12 114

[11]International Electrotechnical Commission 2012 Calibration of Space Charge Measuring Equipment based on the Pulsed Electroacoustic(PEA)Measurement Principle IEC/TS 62758-2012

[12]InternationalElectrotechnicalCommission Measurement of Internal Electric Field In Insulating Materials-Pressure Wave Propagation Method IEC/TR 62836-2013

[13]Mahdavi S,Alquie C,Lewiner J 1989 CEIDP 10 296

[14]Choo W,Chen G,Swingler S G 2011 IEEE Trans.Dielectr.Electr.Insul.18 596

[15]Zheng F H,Zhang Y W,Wu C S,Li J X,Xia Z F 2003 Acta Phys.Sin.52 1137(in Chinese)[郑飞虎,张冶文,吴长顺,李吉晓,夏忠福2003物理学报52 1137]

[16]Hole S 2012 IEEE Trans.Dielectr.Electr.Insul.19 1208

[17]Morsse P M,Ingard K U(translated by Lü R Y,Yang X R)1986 Theoretical Acoustics(Beijing:Science Press)pp299–302(in Chinese)[莫尔斯 P M,英格特K U 著(吕如榆,杨训仁 译)1986理论声学 (北京:科学出版社)第299—302页]

[18]Morsse P M,Ingard K U(translated by Lü R Y,Yang X R)1986 Theoretical Acoustics(Beijing:Science Press)pp420–421(in Chinese)[莫尔斯 P M,英格特K U 著 (吕如榆,杨训仁 译)1986理论声学(北京:科学出版社)第420—421页]

[19]Hu L Q,Zhang Y W,Zheng F H 2005 IEEE Trans.Dielectr.Electr.Insul.12 809

[20]Ma P,Zhang Y W,Holé S,Zheng F H,An Z L 2015 Meas.Sci.Technol.27 025003

[21]Guo C,Zhang Y W,Zheng F H,An Z L,Zhu Z E,Yang L M,Zhang J,Yu E K 2017 1st IEEE International Conference on Electrical Materials and Power Equipment Xi’an,China,May 14–17,2017 p30

PACS:77.22.–d,77.65.Fs,43.20.+g,06.20.–fDOI:10.7498/aps.66.127701

Physical model for space charge distribution measured by pressure wave propagation method in coaxial geometry∗

Sun Ya-Li1)Zhang Ye-Wen1)3)†Stephane Hole1)2)Ma Peng3)Guo Cong1)Zheng Fei-Hu1)An Zhen-Lian1)

1)(Department of Electrical Engineering,Tongji University,Shanghai 201804,China)
2)(ESPCI-ParisTech,Paris 75005,France)
3)(Shanghai Key Laboratory of Special Arti fi cial Microstructure Materials and Technology,Tongji University,Shanghai 200092,China)

15 December 2016;revised manuscript

7 April 2017)

With the rapid development of the science and technology,the application of the high voltage power cable has become more and more extensive.Now,it is generally accepted that space charge has an important e ff ect on the electrical properties of insulating material in a high voltage cable.The measurement of space charge is the research base for the behaviors and properties of space charge in the polymer dielectric.Actually,the pressure wave propagation(PWP)method and pulsed electroacoustic(PEA)method are two sophisticated methods of measuring the space charge.However,these two methods are based on a planar sample.For measuring the space charge in a real cable,it is necessary to need the correct and precise mathematical expressions for the PWP method and PEA method.

According to the theoretical analysis of the space charge distributions in the plate samples,measured by the pressure wave propagation method,we propose a physical model and its mathematical method of treating space charge distribution data measured in a coaxial geometry.In terms of Poisson equation,the in fl uences of pressure waves on coaxial samples can be divided into two parts,namely,sample deformation and particle displacement.These two parts take into consideration the variations of the sample electric fi eld,dielectric constant and density of space charge disturbed by pressure waves.Therefore,the voltage and current equations about the space charge distribution in the coaxial structure are found.The mathematical expression for the current measured indicates that compared with the current measured in the planar structure,which is proportional to the space charge distribution,the current signal measured in the coaxial structure should be further corrected.

This paper also shows the experimental results which are the induced current signals picked from the planar sample and coaxial sample respectively.The results indicate that the current measured in the planar sample is proportional to the space charge distribution.However,the current measured in the planar sample is related to the inner and outer diameter of the dielectric,which veri fi es the correctness of the mathematical expression.

Due to the in fl uence of the coaxial structure of the high voltage cable,the pressure wave focusing e ff ect is obvious as the pressure wave propagates along the axis,which causes the measurement signal to increase gradually with the propagation of sound wave.As a consequence,the electric fi eld and the space charge density will change apparently.Due to the in fl uence of the pressure wave focusing e ff ect,the current and voltage signal will be ampli fi ed more obviously in cable,and the current measured by the PWP method shows the distribution of space charge density in cable.

space charge distribution,pressure wave propagation method,solid dielectric,coaxial structure

10.7498/aps.66.127701

∗国家自然科学基金(批准号:51477118)资助的课题.

†通信作者.E-mail:yewen.zhang@tongji.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant No.51477118).

†Corresponding author.E-mail:yewen.zhang@tongji.edu.cn