多空穴错位分布对石墨纳米带中热输运的影响∗

周欣 高仁斌 谭仕华 彭小芳†蒋湘涛包本刚

1)(中南林业科技大学理学院,长沙 410004)

2)(中南林业科技大学计算机与信息工程学院,长沙 410004)

3)(湖南科技学院教务处,永州 425100)

多空穴错位分布对石墨纳米带中热输运的影响∗

周欣1)高仁斌1)谭仕华1)彭小芳1)†蒋湘涛2)‡包本刚3)

1)(中南林业科技大学理学院,长沙 410004)

2)(中南林业科技大学计算机与信息工程学院,长沙 410004)

3)(湖南科技学院教务处,永州 425100)

(2017年2月22日收到;2017年3月31日收到修改稿)

利用非平衡格林函数方法研究了石墨纳米带中三空穴错位分布对热输运性质的影响.研究结果发现:三空穴竖直并排结构对低频声子的散射较小,导致低温区域三空穴竖直并排时热导最大,而在高频区域,三空穴竖直并排结构对高频声子的散射较大,导致较高温度区域三空穴竖直并排时热导最小;三空穴的相对错位分布仅能较大幅度地调节面内声学模高频声子的透射概率,而三空穴的相对错位分布能较大幅度地调节垂直振动膜高频声子和低频声子的透射概率,导致三空穴的相对错位分布不仅能大幅调节面内声学模和垂直振动模的高温热导,也能大幅调节垂直振动模的低温热导.研究结果阐明了空穴位置不同的石墨纳米带的热导特性,为设计基于石墨纳米带的热输运量子器件提供了有效的理论依据.

非平衡格林函数,声学声子输运,热导,量子体系

1 引 言

近年来,随着微加工技术的不断进步,已能够制造尺寸小于30 nm的低维尺度纳米结构[1,2],一些由硅、黑磷等单元素或硼氮、二硫化钼等多元素构成的二维六角晶体单原子层材料也在实验中被成功制造[3].石墨烯是新型单原子层二维碳纳米材料,自从2004年首次发现以来,由于具有特异的物理和化学性质,例如低能无质量Dirac电子的线性色散关系[4]、已知材料中最强的机械强度[5]、极高的电子迁移率(106cm2/(V·s))等[6]引起了人们的极大兴趣.特别地,由于拥有创记录的极高的热导性质(约3000 Wm/K)[7],石墨烯的热输运性质受到许多科研群体的广泛关注[8−23],利用机械切割、电子束刻蚀等方法[24],石墨烯能够被制备成各种宽度以及各种几何边界的准一维条形量子结构,即石墨纳米带.在这些低维尺度的石墨纳米带中,热导(包括声子热导、电子热导以及光子热导)是量子化的,热导的基本量子化单元是π2k2BT/(3h)(kB是玻尔兹曼常数,h是布朗克常数,T是温度),独立于材料以及载流子性质.研究表明,当石墨纳米带带宽低于10 nm时[1]其具有半导体性质,热导的主要载体是声学声子,由于量子受限制约着声子的色散关系和群速,导致其热导性质有别于体材料.一些科研群体深入研究了基于石墨烯构建的量子结构的热输运性质[15]并发现了许多新奇的热输运现象,例如:缺陷导致的热环流[25]、被突变结构加强的低温热导[26]、不对称三端石墨纳米带结构中的热整流[27,28]、拓扑结构中反常的热导性质[29]等.研究表明,石墨纳米带中的热输运性质与石墨纳米带边缘的粗糙程度[30]、各种缺陷[10−18]、弯曲程度[31]、超晶格[32]、同位素[33]、外力应变以及界面接触[34,35]、结构尺寸[36]、异质结[37]等密切相关,且能被设计成具有优良品质的热电材料[38,39]、高品质的热导调制器[31]、具有负微分效应的热导器件[40].这些研究中空穴对石墨纳米带热输运的调制受到了极大的关注,例如空穴导致的透射深谷[41]、量子环加强的热电性质[42]等.最近,Peng和Chen[18]对比研究了石墨纳米带中空穴对面内声学模(IPMs)与垂直平面声学模(FPMs)的声学声子输运和热导的不同影响,主要阐述了空穴位于石墨纳米带中心位置时对热导的影响.然而实际制备的石墨纳米带中空穴的分布应该是更复杂随机的错位分布情形,而多空穴的错位分布对热导的调制很少见诸报道,有关多空穴的错位分布对热输运的影响的系统研究至今仍然很缺乏.因此,有必要进一步研究错位分布的多空穴结构对热输运的影响,这对于量子器件的设计具有非常重要的物理意义.

众所周知,根据边缘碳原子几何排列的不同,石墨纳米带可以分为扶手椅型石墨纳米带和锯齿型石墨纳米带[22],且在这两种不同种类的石墨纳米带中热输运性质存在明显的差异[43].本文主要关注锯齿型石墨纳米带,研究结果发现三空穴在石墨纳米带中相对旋转或相对平移能大幅调节石墨纳米带中的热导;在低温区域,当三空穴并列且竖直于石墨纳米带横向方位排列时(即竖直并排结构,如图1所示)热导最大,而在高温区域三空穴竖直并排结构的热导最小;三空穴的相对位置变化仅能大幅调节IPMs高频声子的透射概率和高温热导,而三空穴的相对位置变化不仅能大幅调节垂直振动模高频声子的透射概率和高温热导,也能大幅调节垂直振动模低频声子的透射概率和低温热导.上述结果为这个领域提供了新的内容,有助于研究人员从理论和实验上更深入地理解相关结构中的声学声子输运和热导性质.

2 理论模型与公式

图1为含三个空穴锯齿型石墨纳米带的模型图,分为3个区域,根据Landauer公式和线性响应假设,石墨纳米带中的热流可以写为

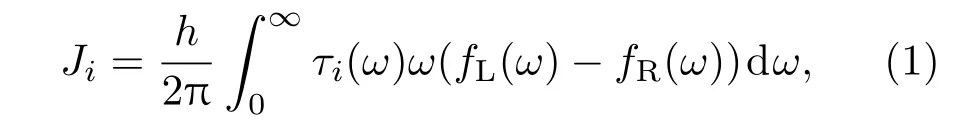
其中fL/R(ω)=1/[exp(hω/kBTL/R)− 1]是石墨纳米带中的声子Bose-Einstein分布函数,τi(ω)是第i支模的声子从左至右穿越散射区域的透射系数.图1左边红色区域(L)是温度为T1的能量输入热库,中间是声子散射区域(C),右边蓝色区域(R)是温度为T2的能量输出热库.假设温度差δT(δT=T1−T2>0)趋近于0,则可直接采用平均温度T[T=(T1+T2)/2]计算.由于常温下石墨烯的声子平均自由程远大于同等尺寸大小的含空穴的石墨烯纳米带GNRs的平均自由程,所以电-声相互作用忽略不计.在弹性散射近似下,计算热导的公式可写为

其中,β=1/(kBT).研究表明[18],石墨纳米带中存在两种声学模:IPMs和FPMs,且这两种声学模的耦合可以忽略.因此,其哈密顿方程可表示为

石墨纳米带中总的声子透射概率和热导可分解为IPMs和FPMs的声子透射概率和热导,并可对其进行独立计算.

图1 (网刊彩色)具有三个空穴的锯齿型石墨纳米带的结构示意图Fig.1. (color online)Schematics zigzag graphene nanoribbons with three cavities.

在谐波近似的情况下,FPMs的哈密顿方程可表示为

IPMs的哈密顿方程表示为

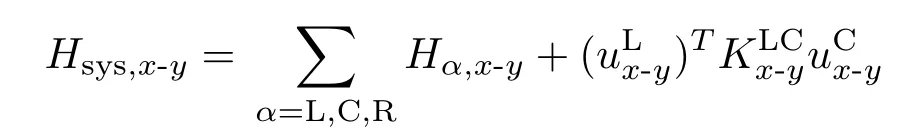
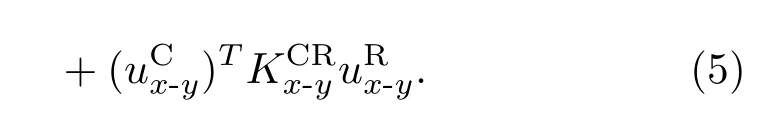
由于Brenner’s经验势,可以在β计算碳原子之间的力常数,对于FPMs,完整线性系统的动力矩阵可表示为

IPMs的动力矩阵可表示为

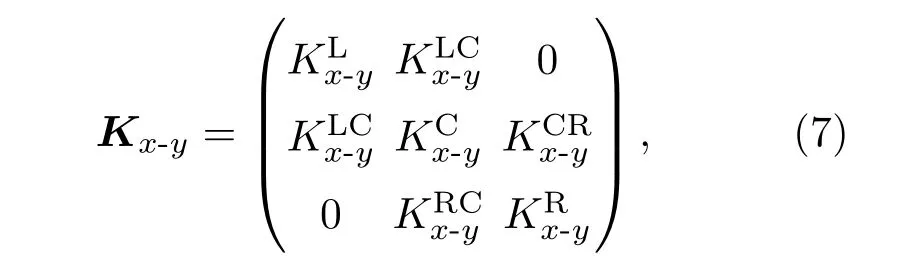
通过非平衡格林函数方法,FPMs的格林函数可以写成

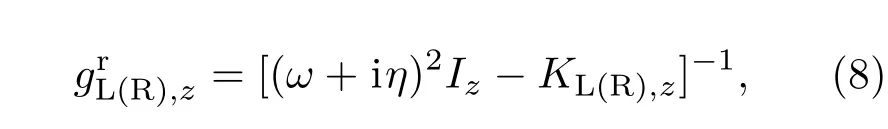
IPMs的格林函数可以写成

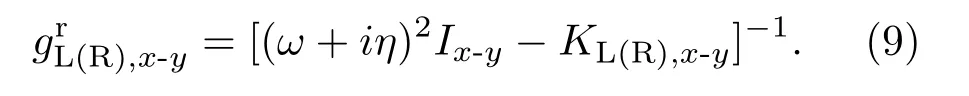
本文中计算声子的透射概率τi是计算热导的关键,FPMs的透射概率可以表示为

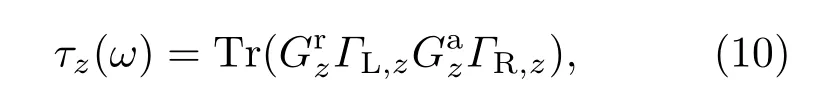
IPMs的透射概率表示为

其 中ΓL(R),z = −2ImΣL(R),z和ΓL(R),x-y =−2ImΣL(R),x-y分别是在IPMs和FPMs中作为能量输入端和能量输出端的接触扩展函数,Gr(a)z和Gr(a)x-y分别是IPMs和FPMs中间散射区域的推迟/超前格林函数,分别表示为

其中,Gaz=(Grz)+和Gax-y=(Grx-y)+,通过上述方法可计算出该结构中的声子透射概率和热导.

3 数值结果和分析

图2描述了宽度n=15且含三个空穴的石墨纳米带中总的约化热导随温度的变化关系.从图2(a)和图2(c)可以看到,当温度趋近于0 K时,约化热导总是趋近于3,这与三个空穴在量子结构中的分布位置无关,是由于当T→0时,仅有三支截止频率为零的长波长声学模被激发,即两支截止频率为零的IPMs和一支截止频率为零的FPMs,这些长波长声学声子的波长远长于散射结构的结构尺寸,散射结构对长波长声学声子的散射很小的缘故.随着温度的升高,频率较大的IPMs和FPMs被激发,入射声子与被结构反射回的声子相互作用,导致透射谱呈现振荡透射峰-谷结构;同时,这些较大频率的声学声子被散射结构散射,使声子透射概率降低,导致约化热导随着温度的升高而降低.随着温度的继续升高,截止频率大于零的声学模被激发,总的声子透射概率明显增大,因此约化热导也随温度的升高而增大.比较图2(a)中的实线、划线、点线、点划线发现,三空穴的不同位置分布对应的热导曲线存在明显的区别:从内插图中可以看出,在极低的温度区域(0—6 K),三空穴竖直并排时热导最大,当空穴1和空穴3以空穴2为中心旋转时,约化热导随之降低;而在较高的温度区域,三空穴竖直并排时热导最小,当空穴1和空穴3以空穴2为中心旋转时,约化热导明显增大;而且随着温度的升高,它们的约化热导差值也随着扩大.这些热导性质能从图2(b)中相对应的透射谱得到很好的解释:在低频区域,虽然散射结构对低频声子的散射导致了这些声子的透射都呈现不规则的峰-谷结构,但是在图2(b)中可清楚地看到,当三空穴竖直并排时对声子的散射影响最小,因此声子透射相对较大,从而导致约化热导在低温区域相对较高;而在高频区域,三空穴竖直并排时对声子的透射概率明显低于旋转后的结构或者旋转后并平移的结构对声子的透射概率,因而导致三空穴竖直并排时的高温热导明显低于旋转后的结构或者旋转后并平移的结构的热导.观察图2(a)和图2(c)所示的热导曲线,不仅发现三空穴竖直并排时的约化热导总是在低温区域最大,在高温区域最小,还发现两幅图中三空穴竖直并排时的约化热导相对较大的低温度区域范围却不一致:从内插图中可以看出,图2(a)的低温度范围为0—6 K,而图2(c)的低温度范围为0—15 K.三空穴竖直并排结构与旋转空穴结构的透射谱比较发现,三空穴竖直并排结构对应的透射曲线相对较大区域的范围为0—10 cm−1(图2(b)),而三空穴竖直并排结构与平移空穴结构的透射谱比较发现,三空穴竖直并排结构对应的透射曲线较大区域的范围为0—30 cm−1(图2(d)).这表明,空穴的平移对低频声子的散射比空穴的旋转对低频声子的散射影响更大,因而导致较大温度范围内更低的低温热导.这些研究表明,空穴结构在量子线中的分布能明显调节量子线中的热导.

图2 (网刊彩色)(a),(b)锯齿型石墨纳米带中三空穴分布为图1结构(实线),以图1结构中的空穴2为中心,空穴1和3旋转49◦(短划线),90◦(点线),以及旋转90◦后三个空穴整体下移6α(点划线)时,总的约化热导随温度的变化以及总的√透射概率随频率√的变化;(c),(d)锯齿型石墨纳√米带中三空穴分布为图1结构(实线√),图1结构中固定空穴3,空穴2右移43α(短划线),83α(点线),以及空穴2右移83α后再下移6α,且空穴1右移43α(点划线)时,总的约化热导随温度的变化以及总的透射概率随频率的变化;α是原子间的键长;内插图表示相对应结构中低温区域的约化热导和低频区域的透射概率Fig.2.(color online)(a),(c)The total reduced thermal conductance as a function of temperature;(b),(d)the total transmission rate as a function of frequency;in panels(a),(b),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the case shown in Fig.1,dashed and dotted curves respectively correspond to the cases that the cavities 1 and 3 rotate 49◦and 90◦about the cavity 2 fi xed as the centre in Fig.1,dash-dotted curves correspond to the case that the cavities 1 and 3 fi rst rotate 90◦about the cavity 2,and then the three cavities move down 6α;in panels(c),(d),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the √case shown√ in Fig.1,dashed and dotted curves respectively correspond to the cases that the cavity 2 move right 43α and 83α w√hen the cavity 3 is fi xed in Fig.1,dash-dotted curves corres√pond to the case that the cavity 2 fi rst moves right 83α and then moves down 6α,and the cavity 1 moves right 43α.Here,α is the bond length between the atoms.The insets describe thetotalreducedthermalconductancein the low temperatureregion andthe total transmissionrate in the low frequency region,respectively.

为了研究空穴在石墨纳米带中不同位置分布对IPMs和FPMs热输运性质的影响,图3给出了IPMs和FPMs的透射谱.从图3可清楚地看到当频率趋近于0 K时,IPMs与FPMs的透射概率分别趋近于2和1,这是由于分别有两支截止频率为零的长波长IPMs与一支截止频率为零的FPMs被激发的缘故.随着频率的增加,截止频率大于零的高频声学支被激发,这些被激发的声学模被散射结构散射后与入射模相互作用,导致出现复杂的透射峰-谷结构.然而IPMs的透射谱的峰-谷结构的振荡剧烈程度明显大于FPMs,这是由于在高频区域,面内的横向声学模与纵向声学模都被激发且相互耦合,而面内被激发的IPMs明显多于FPMs,因此更多被激发的IPMs耦合导致其呈现振荡更加剧烈的透射峰-谷结构.此外,研究发现,虽然三空穴的平移与旋转都能调节IPMs与FPMs的透射概率,然而对这两类振动模的调节幅度也存在明显的差异:三空穴的相对位置改变对IPMs的低频范围的声子透射调节不是很明显,而对高频范围的声子透射调节却较大;而三空穴的相对位置改变对FPMs的低频区域与高频区域的声学声子的透射概率的调节都非常大.这些研究表明可通过调节空穴的不同位置分布来有区别地调制IPMs与FPMs的透射概率.

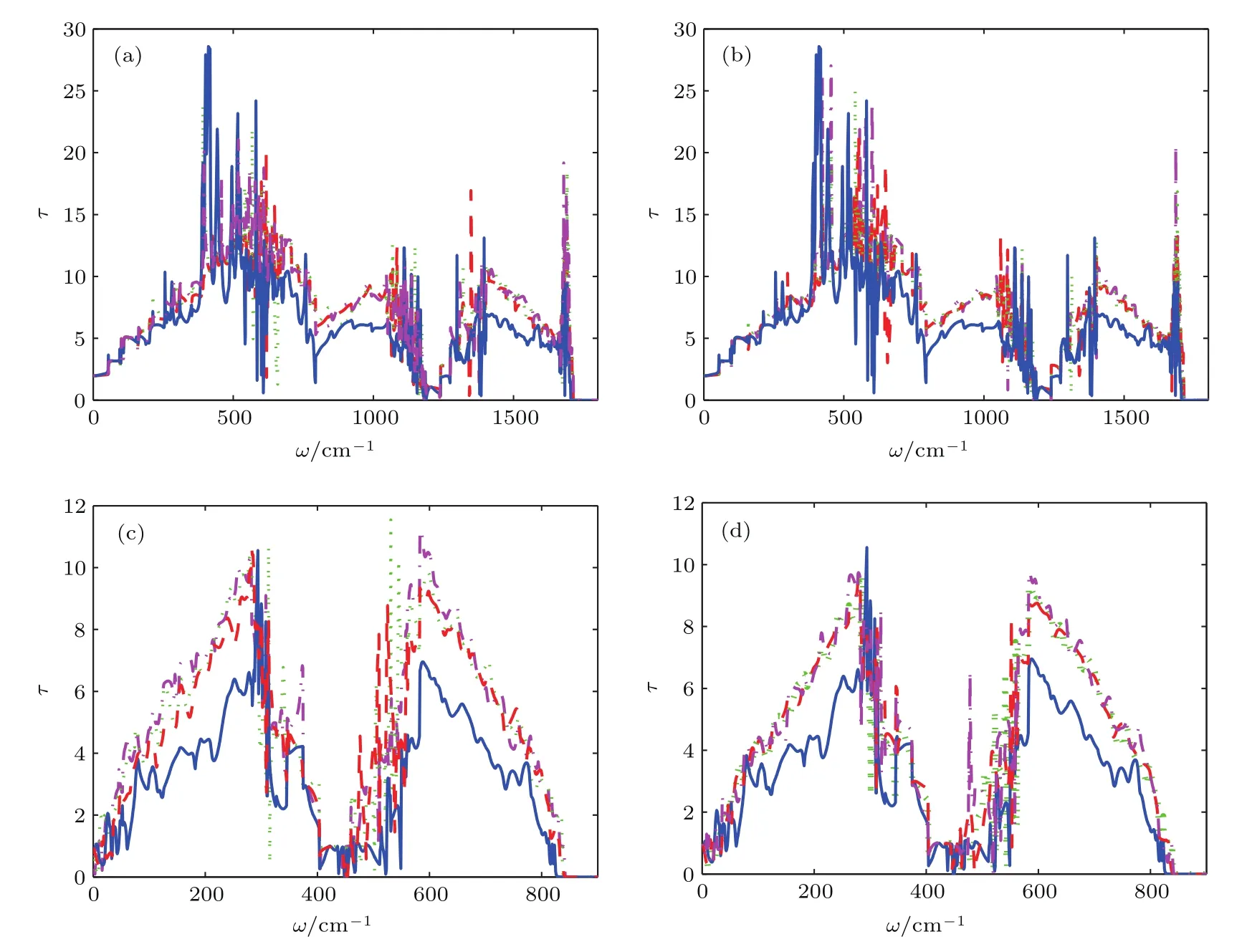
图3 (网刊彩色)(a),(c)锯齿型石墨纳米带中三空穴分布为图1结构(实线),以图1结构中的空穴2为中心,空穴1和3旋转49◦(短划线),90◦(点线),以及旋转90◦后三个空穴整体下移6α(点划线)时,IPM√s和FPMs的透√射概率;(b),(d)锯齿型石墨纳√米带中三空穴分布为图1结构(实√线),图1结构中固定空穴3,空穴2右移43α(短划线),83α(点线),以及空穴2右移83α后再下移6α,且空穴1右移43α(点划线)时,IPMs和FPMs的透射概率Fig.3.(color online)The transmission rates of IPMs(panels(a),(b))and FPMs(panels(c),(d));in panels(a),(c),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the case shown in Fig.1,dashed and dotted curves respectively correspond to the cases that the cavities 1 and 3 rotate 49◦and 90◦about the cavity 2 fi xed as the centre in Fig.1,dash-dotted curves correspond to the case that the cavities 1 and 3 fi rst rotate 90◦about the cavity 2,and then the three cavities move down 6α;in panels(b),(d),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the√ case shown√ in Fig.1,dashed and dotted curves respectively correspond to the cases that the cavity 2 move right 43α and 83α w√hen the cavity 3 is fi xed in Fig.1,dash-dotted curves corresp√ond to the case that the cavity 2 fi rst moves right 83α and then moves down 6α,and the cavity 1 moves right 43α.

图4 (网刊彩色)(a),(c)锯齿型石墨纳米带中三空穴分布为图1结构(实线),以图1结构中的空穴2为中心,空穴1和3旋转49◦(短划线),90◦(点线),以及旋转90◦后三个空穴整体下移6α(点划线)时,IPM√s和FPMs的约√化热导;(b),(d)锯齿型石墨纳√米带中三空穴分布为图1结构(实线√),图1结构中固定空穴3,空穴2右移43α(短划线),83α(点线),以及空穴2右移83α后再下移6α,且空穴1右移43α(点划线)时,IPMs和FPMs的约化热导Fig.4.(color online)The reduced thermal conductance of IPMs(panels(a),(b))and FPMs(panels(c),(d));in panels(a),(c),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the case shown in Fig.1,dashed and dotted curves respectively correspond to the cases that the cavities 1 and 3 rotate 49◦and 90◦about the cavity 2 fi xed as the centre in Fig.1,dash-dotted curves correspond to the case that the cavities 1 and 3 fi rst rotate 90◦about the cavity 2,and then the three cavities move down 6α;in panels(b),(d),for the distributions of three cavities of zigzag graphene nanoribbons,solid curves correspond to the√ case show√nin Fig.1,dashed and dotted curves respectively correspond to the cases that the cavity 2 move right 43α and 83α w√hen the cavity 3 is fi xed in Fig.1,dash-dotted curves corresp√ond to the case that the cavity 2 fi rst moves right 83α and then moves down 6α,and the cavity 1 moves right 43α.

图4给出了IPMs与FPMs的约化热导随温度的变化.从图4可以看出,当温度趋近于0 K时,IPMs与FPMs的约化热导分别趋近于2和1且不受散射区域的影响,这是由于温度趋近于0 K时只有两支起振频率为零的面内长波长声学模和一支起振频率为零的垂直平面长波长振动声学模被激发的缘故.在极低温度范围(0—10 K)内约化热导随温度的升高呈现下降的趋势,这是由于随着温度的升高,一些高频声子被激发,被激发的高频率声子被散射,结构散射导致了约化热导的下降,随着温度的进一步上升,起振频率大于零的高频声学支被激发,约化热导迅速上升.对于IPMs,不管是两空穴绕中间空穴的相对旋转,还是空穴间的相对平移,在约0—150 K的温度范围内,约化热导几乎不受影响.这是因为低温范围的热导主要由低频声子的输运贡献.从图3(a)和图3(b)可以看到,IPMs模的低频声子的输运几乎不受空穴在量子线中的相对错位的影响,因此热导也几乎不受空穴相对错位的影响,包括空穴间的相对平移和相对旋转.而在温度大于150 K的相对高温区域,大量高频声子被激发,热导主要是由高频声子的输运而贡献的.从图3(a)和图3(b)所示透射谱可清晰地看到,高频声子的透射明显依赖于空穴在量子线中的位置分布.因此,IPMs贡献的高温热导也依赖于空穴在量子线中的位置分布.而对于FPMs贡献的热导在低温到高温范围都高度依赖于三空穴的相对旋转以及相对平移,这是由于FPMs的透射概率在低频范围和高频范围都高度依赖于这些空穴的相对平移和旋转,这一点可清楚地从图3(c)和图3(d)中看到.比较图4(c)和图4(d),可看到三空穴的相对旋转对FPMs约化热导的调节效果比三空穴的相对平移对FPMs约化热导的调节效果明显.这是由于三空穴的相对旋转对FPMs高频声子的透射概率的影响大于三空穴的相对平移对FPMs高频声子的透射概率的影响.这些研究表明,可通过空穴平移或旋转来分别调制IPMs与FPMs的约化热导.

4 结 论

采用非平衡格林函数方法,在保持石墨纳米带带宽不变的情况下,研究了存在三个空穴的石墨纳米带中弹性声学声子输运和热导特性,得到了一些有趣的物理结果:1)三空穴竖直并排结构对低频声子的散射较小,导致低温区域三空穴竖直并排时热导最大;2)三空穴竖直并排结构对高频声子的散射较大,导致在较高温度区域三空穴竖直并排时热导最小;3)三空穴的相对错位分布仅能较大幅度地调节IPMs高频声子的透射概率,导致三空穴的相对平移或旋转仅能大幅调节IPMs的高温热导;4)三空穴的相对错位分布能较大幅度地调节FPMs的高频声子和低频声子的透射概率,导致三空穴的相对平移或旋转不仅能大幅调节FPMs的高温热导,也能大幅调节FPMs的低温热导.此研究结果可为设计基于石墨纳米带的热量子器件提供有价值的物理模型和理论参考.

[1]Li X,Wang X,Zhang L,Lee S,Dai H 2008 Science 319 1229

[2]Chen X B,Duan W H 2015 Acta Phys.Sin.64 186302(in Chinese)[陈晓彬,段文晖 2015物理学报 64 186302]

[3]Zhai X C,Qi F H,Xu Y F,Zhou X F,Jin G J 2015 Prog.Phys.35 1(in Chinese)[翟学超,戚凤华,许亚芳,周兴飞,金国钧2015物理学进展35 1]

[4]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 109

[5]Lee C,Wei X,Kysar J W,Hone J 2008 Science 321 385

[6]Du X,Skachko I,Barker A,Andrei E Y 2008 Nat.Nanotechnol.3 491

[7]Balandin A A 2011 Nat.Mater.10 569

[8]Peng X F,Wang X J,Gong Z Q,Chen K Q 2011 Appl.Phys.Lett.99 233105

[9]Peng X F,Zhou X,Tan S H,Wang X J,Chen K Q 2017 Carbon 113 334

[10]Tan S H,Tang L M,Xie Z X,Pan C N,Chen K Q 2013 Carbon 65 181

[11]Chen X K,Xie Z X,Zhou W X,Tang L M,Chen K Q 2016 Appl.Phys.Lett.109 023101

[12]Chen K Q,Li W X,Duan W,Shuai Z,Gu B L 2005 Phys.Rev.B 72 045422

[13]Peng X F,Chen K Q,Wan Q,Zou B S,Duan W 2010 Phys.Rev.B 81 195317

[14]Xu Y,Chen X,Wang J S,Gu B L,Duan W 2010 Phys.Rev.B 81 195425

[15]Xu Y,Li Z,Duan W 2014 Small 10 2182

[16]Xu W,Zhang G,Li B 2015 J.Chem.Phys.143 154703

[17]Xu Y,Tang P,Zhang S C 2015 Phys.Rev.B 92 081112

[18]Peng X F,Chen K Q 2014 Carbon 77 360

[19]Peng X F,Chen K Q 2016 Carbon 100 36

[20]Yao H F,Xie Y E,Ou Y T,Chen Y P 2013 Acta Phys.Sin.62 068102(in Chinese)[姚海峰,谢月娥,欧阳滔,陈元平2013物理学报62 068102]

[21]Hua Y C,Cao B Y 2015 Acta Phys.Sin.64 146501(in Chinese)[华钰超,曹炳阳 2015物理学报 64 146501]

[22]Ouyang F P,Xu H,Li M J 2008 Acta Phys.Chim.Sin.24 328(in Chinese)[欧阳方平,徐慧,李明君2008物理化学学报24 328]

[23]Huang W Q,Huang G F,Wang L L,Huang B Y 2007 Phys.Rev.B 75 233415

[24]Bao Z G,Chen Y P,Ouyang T,Yang K K,Zhong J X 2011 Acta Phys.Sin.60 028103(in Chinese)[鲍志刚,陈元平,欧阳滔,杨凯科,钟建新2011物理学报60 028103]

[25]Morooka M,Yamamoto T,Watanabe K 2008 Phys.Rev.B 77 033412

[26]Peng X F,Wang X J,Chen L Q,Chen K Q 2012 Europhys.Lett.98 56001

[27]Ouyang T,Chen Y,Xie Y 2010 Phys.Rev.B 82 245403

[28]Yang N,Zhang G,Li B 2009 Appl.Phys.Lett.95 033107

[29]Liu X J,Zhang G,Zhang Y W 2016 Nano Lett.16 4954

[30]Sevincli H,Cuniberti G 2010 Phys.Rev.B 81 113401

[31]Ouyang T,Chen Y,Xie Y,Stocks G M,Zhong J X 2011 Appl.Phys.Lett.99 233101

[32]Zhu T,Ertekin E 2014 Phys.Rev.B 90 195209

[33]Ouyang T,Chen Y P,Yang K K,Zhong J X 2009 Europhys.Lett.88 28002

[34]Chen J,Zhang G,Li B 2013 Nanoscale 5 532

[35]Chen J,Walther J H,Koumoutsakos P 2014 Nano Lett.14 819

[36]Peng X F,Xiong C,Wang X J,Chen L Q,Luo Y F,Li J B 2013 Comput.Mater.Sci.77 440

[37]Pan C N,Xie Z X,Tang L M,Chen K Q 2012 Appl.Phys.Lett.101 103115

[38]Zheng H,Liu H J,Tan X J,Lü H Y,Pan L,Shi J,Tang X F 2012 Appl.Phys.Lett.100 093104

[39]Huang W,Wang J S,Liang G 2011 Phys.Rev.B 84 045410

[40]Hu J,Wang Y,Vallabhaneni A,Ruan X,Chen Y P 2011 Phys.Rev.B 99 113101

[41]Xie Z X,Chen K Q,Duan W H 2011 J.Phys.-Condens.Matter 23 315302

[42]Bretin M S,Malyshev A V,Orellana P A,Dominguez Adame F 2015 Phys.Rev.B 91 085431

[43]Xu Y,Chen X,Gu B L,Duan W 2009 Appl.Phys.Lett.95 233116

PACS:63.22.Rc,73.23.Ad,44.10.+iDOI:10.7498/aps.66.126302

In fl uence of multi-cavity dislocation distribution on thermal conductance in graphene nanoribbons∗

Zhou Xin1)Gao Ren-Bin1)Tan Shi-Hua1)Peng Xiao-Fang1)†Jiang Xiang-Tao2)‡Bao Ben-Gang3)

1)(Institute of Mathematics and Physics,Central South University of Forestry and Technology,Changsha 410004,China)
2)(Institute of Computer and Information Engineering,Central South University of Forestry and Technology,Changsha 410004,China)
3)(Office of Academic A ff airs,Hunan University of Science and Engineering,Yongzhou 425100,China)

22 February 2017;revised manuscript

31 March 2017)

Using non-equilibrium Green’s function method and keeping the zigzag carbon chains unchanged,we investigate the transmission rate of acoustic phonon and the reduced thermal conductance in the graphene nanoribbons with three cavities.The results show that the reduced thermal conductance approaches to 3π2k2BT/(3h)in the limit T → 0 K.Due to the fact that only long wavelength acoustic phonons with zero cuto fffrequency are excited at such low temperatures,the scattering in fl uence on the long wavelength acoustic phonons by the dislocation distribution of three cavities in the graphene nanoribbons can be ignored and these phonons can go through the scattering region perfectly.As the temperature goes up,the reduced thermal conductance decreases.This is because the high-frequency phonons are excited and these high-frequency phonons are scattered easily by the scattering structures.With the further rise of temperature,acoustic phonon modes with the cuto fffrequency greater than zero are excited,which leads to a rapid increase of the reduced thermal conductance.This study shows that in higher frequency region,the transmission spectra display complex peak-dip structures,which results from the fact that in higher frequency region,more phonon modes are excited and scattered in the middle scattering region with three cavities,and the scattering phonons are coupled with the incident phonons.When the three cavities are aligned perpendicularly to the edge of the graphene nanoribbons,the scattering from low-frequency phonons by the scattering structures is smallest,which leads to the fact that the reduced thermal conductance is largest at low temperatures;however,at high temperatures,the reduced thermal conductance is smallest when the three cavities is aligned perpendicularly to the edge of the graphene nanoribbons.This is because the scattering from high-frequency phonons by the scattering structures is biggest.These results show that the acousticphonon transport and the reduced thermal conductance are dependent on the relative position of the three cavities.In addition,the dislocation distribution of the three cavities can only modulate obviously the high-temperature thermal conductance of the in-plane modes(IPMs).This is because the change of the relative position of the quantum dots can only modulate greatly the high-frequency phonon transmission rate and less modulate the low-frequency phonon transmission rate of the IPMs.However,the dislocation distribution of the three cavities can adjust obviously not only the high-temperature thermal conductance of the fl exural phonon modes(FPMs),but also the low-temperature thermal conductance of the FPMs.This is because the change of the relative position of the three cavities can modulate greatly phonon transmission rates of fl exural phonon modes in the low-frequency and high-frequency regions.These results provide an e ff ective theoretical basis for designing the thermal transport quantum devices based on graphene nanoribbons.

nonequilibrium Green’s functions,acoustic phonon transport,thermal conductance,quantum system

10.7498/aps.66.126302

∗国家自然科学基金(批准号:11247030,61272147,61602529)、湖南省自然科学基金(批准号:14JJ4054)、湖南省教育厅基金(批准号:12B136,12C0446)、中南林业科技大学人才引进计划(批准号:104-0160)和中南林业科技大学研究生科技创新基金(批准号:CX2016B26)资助的课题.

†通信作者.E-mail:xiaofangpeng11@163.com

‡通信作者.E-mail:xtjiang@csuft.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.11247030,61272147,61602529),the Hunan Provincial Natural Science Foundation,China(Grant No.14JJ4054),the Research Foundation of Hunan Provincial Education Department,China(Grant Nos.12B136,12C0446),the Talent Introducing Foundation of Central South University of Forestry and Technology,China(Grant No.104-0160),and the Scienti fi c Innovation Fund for Graduate of Central South University of Forestry and Technology,China(Grant No.CX2016B26).

†Corresponding author.E-mail:xiaofangpeng11@163.com

‡Corresponding author.E-mail:xtjiang@csuft.edu.cn