基于摩擦特性的榫接合节点抗拔力研究

胡文刚，关惠元

(南京林业大学家居与工业设计学院，南京210037)

基于摩擦特性的榫接合节点抗拔力研究

胡文刚，关惠元*

(南京林业大学家居与工业设计学院，南京210037)

通过创新的测量方法对椭圆榫接合节点的摩擦特性进行了研究，基于合理的条件假设，建立了椭圆榫接合节点抗拔力的数学模型，并通过椭圆榫接合T形构件的抗拔力试验对模型计算结果进行了检验。研究结果表明，基于本研究所采用的加工方式，木材在平面接触状态下，接触面纹理角度、接触面积以及接触压力对木材与木材间的摩擦系数无明显影响。各接触面粗糙度测量结果表明，横纹不同纹理角度和顺纹不同纹理角度下的粗糙度基本相等。通过创新的试验方法对不同纹理角度的椭圆榫接合节点摩擦系数进行测量，其结果与平面接触状态下的测量结果基本一致，平均摩擦系数约为0.54。试验验证阶段对采用椭圆榫接合的T形构件抗拔力进行了测量，得到抗拔力平均值为3 192.5 N，标准差为398 N，而通过本研究建立的数学模型计算所得的榫接合节点抗拔力为2 928.08 N。数学模型计算结果与试验结果的最大值及最小值的误差均在标准差范围内。因此，本研究所建立的力学模型可用于实木椭圆榫接合节点抗拔力的估算，并为榫接合节点在胶合状态下的力学特性研究，以及实木榫接合家具结构设计提供依据。

榫接合；摩擦系数；抗拔力；数学模型

榫接合作为我国传统实木家具的主要连接方式被沿用至今，不采用任何金属五金及胶黏剂，仅凭榫孔与榫头之间的紧密配合，就能达到理想的接合强度。前人对实木榫接合力学性能的研究主要集中于影响榫接合节点强度的因素，如配合参量[1-2]、节点形式[3-4]、胶黏剂种类和厚度[5-6]以及不同树种等[7]，对影响节点强度的深层因素研究相对较少，如节点间的摩擦特性以及胶合界面特性[8]等。张莲洁等[9]以库仑定律为原理对不同木质材料间的摩擦系数进行了研究，发现木材比重与材料间摩擦系数存在一定的负相关性。此外，木材间的摩擦系数与加工方式有密切联系，研究表明，随着刀具转速的增加，尤其在高转速下，木材表面间的摩擦系数有降低趋势[10-11]。在木质胶合产品的加工工艺选择与使用性能评价中，胶黏剂渗透性能和界面力学性能是重要的评判标准[12]，但在榫接合节点强度方面的研究较少。

笔者仅对影响榫接合节点摩擦特性的因素进行了研究，通过创新的测量方法得到了节点的摩擦系数，并通过表面粗糙度对其进行了检验；随后，通过合理假设提出了基于摩擦特性的榫接合节点抗拔力数学模型；最后，通过试验测得榫接合节点的抗拔力，并与数学模型计算结果进行了对比分析。

1 材料与方法

1.1 试验材料与设备

榉木(Zelkovaserrata(Thunb.) Makino)，购自本地木材商，含水率11.91%～12.03%，气干密度0.69～0.71 g/cm3。AG-X型万能力学实验机，日本岛津公司；TR240型粗糙度测试仪，上海速雷电力仪器公司；WPC型数控机床，加工精度为0.01 mm，上海原力数控机电有限公司。

1.2 试件及加工方法

本研究中所有试件均采用数控机床进行加工。在摩擦系数影响因素研究阶段，采用平面接触状态进行研究，各接触面纹理角度如表1所示，其中，试件1的尺寸为35 mm×35 mm×18 mm，试件2的尺寸为70 mm×45 mm×18 mm。表中试件长度方向为数控机床刀具的进给方向，试件1为不同纹理角度榫孔接触面，试件2为不同纹理角度榫头接触面。同时，在加工过程中保证平面试件分别与榫头及榫孔的纹理角度和加工路径一致，且在试验过程中试件1滑动方向与榫头拔出方向相同。

在平面接触状态研究基础之上，采用图1所示的试件，按照榫接合试件的真实尺寸分别制作榫孔及榫头，保证配合量与真实榫接合抗拔力测试试件相同。将榫孔从中部剖开，并用胶黏剂将榫头与榫孔的一半进行黏结，另一部分榫孔可自由滑动。同时，为保证加载时配重能够稳定地放置于试件节点处，本研究采用了双椭圆榫的形式，测定了5 kg配重下不同纹理角度的榫接合节点摩擦系数。

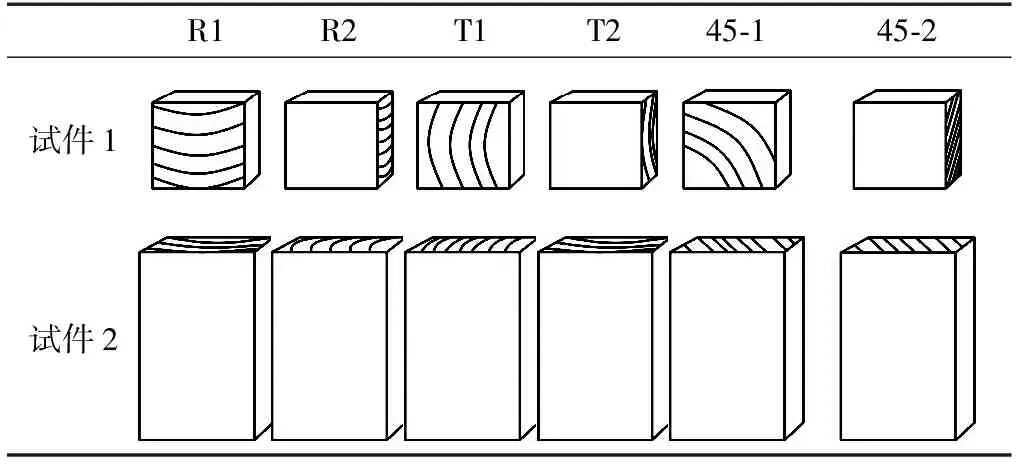
表1 接触对组合

图1 摩擦系数测量试件Fig. 1 Specimen of measuring friction coefficient

榫接合抗拔力测量试件为椭圆榫接合的T形构件，试件尺寸如图2所示。其中，腿部与拉挡的截面纹理均为径向(R)；榫头宽度与榫孔长度方向为过盈配合，过盈量为0.12 mm；榫头厚度方向与榫孔宽度方向为间隙配合，间隙为0.2 mm。

1.3 试验方法

基于库仑摩擦定律测量木材与木材界面的摩擦系数，通过万能力学试验机配合自行设计的测量装置进行测量(图3)，加载速度为1 mm/min。底板通过螺栓固定在试验机底部，试验机加载接口与试验机相连，通过转向机构和钢丝绳将竖直方向的拉力转为水平方向。配重与试件1共同作为正压力，在钢丝绳的牵引力下在试件2表面滑动。当试件1由静止开始滑动时，即可测得试件1与试件2的静摩擦系数μ，这也是两者间的最大滑动摩擦系数，计算公式如式(1)，试验前需测量转向机构的效率。

μ=Fp/[(m1+m2)g]

(1)

式中：F为力学试验机显示的拉力，N；p为定滑轮的效率；m1为配重质量、m2为试件1质量，kg；g为重力加速度。

分别研究了正压力、接触面纹理角度及接触面积等因素对摩擦系数的影响，配重分别为2，5和8 kg。接触面纹理角度如表1所示，接触面尺寸分别为25 mm×25 mm、25 mm×35 mm和35 mm×35 mm，每个水平分别测量10次。试验采用逐层递进的研究方法，首先研究了配重及木材纹理角度对摩擦系数的影响，如其中某一因素对摩擦系数无显著影响，则在研究另一因素对摩擦系数的影响时，将此因素固定，以此类推，逐步研究各因素对木材摩擦系数的影响。

测量木材表面粗糙度时，分别对6组接触对的9种(其中有3种相同)平面进行测量，每个试件上均匀取三点测量榫头拔出方向的粗糙度，每种平面制作6个试件，测量18次。椭圆榫接合抗拨力测试时,试验机加载速度为5 mm/min，共测量20个试件，记录榫头被拔出时载荷的最大值。

图3 摩擦系数测量装置Fig. 3 Equipment of measuring friction coefficient

2 椭圆榫节点抗拔力的数学模型

椭圆榫在接合时，因其接触面为曲面，导致应力分布不均匀，这主要是由于榫头装入榫孔时不同部位的变形量不一致所造成的，通过常规设备很难对其进行测量。为了计算椭圆榫接合节点的应力分布，笔者做出以下合理的模型假设，并建立了椭圆榫节点抗拔力的数学模型。

2.1 模型假设

数学模型是建立在一些合理假设前提下的科学和工程模型，本研究中所建立的榫接合节点表面应力分布模型则基于以下假设条件：

1)根据现有的实木榫接合工艺，榫头宽度方向与榫孔长度方向(y轴)为过盈配合，榫头厚度方向和榫孔宽度方向(x轴)为间隙配合，如图4所示。因过盈量较小，故假设其为弹性变形，同时，在榫头被压缩后，横向(x轴)会产生微小变形，但横向为间隙配合，因此假设横向榫头直线部分与榫孔并无接触，或虽接触但接触压力较小，导致产生的摩擦力更小，故模型中对其进行了忽略，仅考虑过盈配合的圆弧段摩擦力。

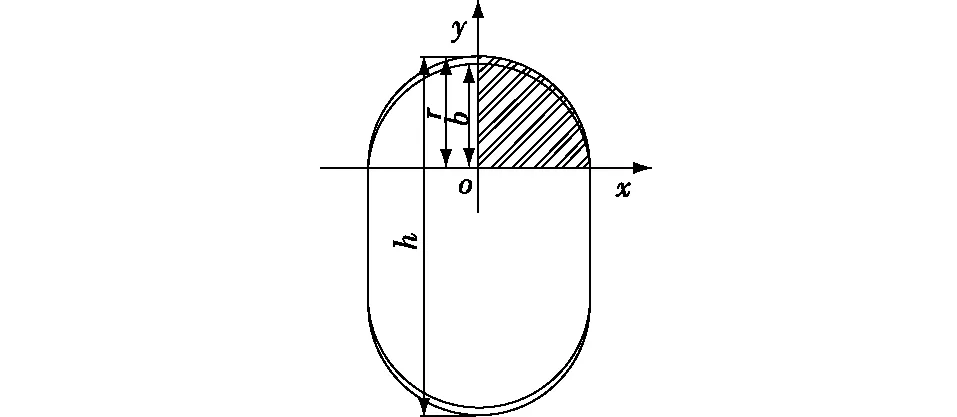
图4 数学模型示意图Fig. 4 Schematic of mathematic model

2)假设榫头与榫孔过盈配合时，榫孔不产生变形且榫头为弹性变形[1]。根据常规实木家具榫接合构件垂直接合的工艺(图2)，榫孔圆弧表面受力方向为木材顺纹方向，而榫头圆弧表面受力方向为榫头的横纹方向。根据榉木压缩强度测试可知，顺纹抗压强度约为径向的4倍、弦向的10倍，此结论与《中国主要树种的木材力学性质》[13]中所列的木材的压缩强度具有较好一致性，且榫孔与榫头配合时过盈量较小，故此假设具有一定合理性。

3)假设装配后榫头与榫孔表面完全接触，无缝隙。此假设基于宏观尺度，在过盈配合产生的压力作用下，两者可视为完全接触。

4)假设沿榫头长度方向任意圆弧线段上的应力分布相同。因榫头可看作是由椭圆截面沿榫头长度方向拉伸得到，故此假设具有一定合理性。

2.2 模型建立

基于以上假设，只需求得榫头上任意圆弧线段上的应变分布函数，即可建立椭圆榫圆表面的应力分布数学模型。以椭圆榫上半表面圆弧线段为例，如图4斜线阴影部分所示，设榫头与榫孔的过盈量为2Δb。未组装时，榫头圆弧线段上各点的方程如式(2)所示；组装后，榫头截面变为椭圆形，其方程如式(3)所示。设榫头圆弧最顶端(榫头变形量最大处)的应变为ε0，其计算公式如式(4)和(5)所示；榫头变形后表面各点的应变可表示为方程(6)，结合物理方程(7)可得到椭圆榫截面的应力分布函数(8)。

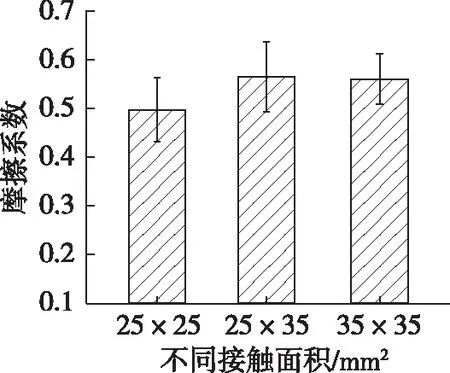
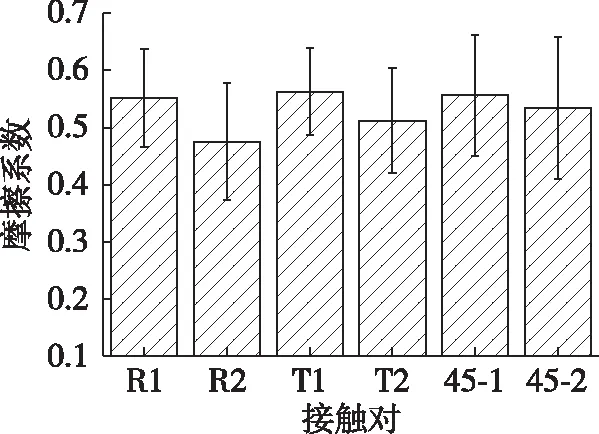
x2+y2=r2, 0

(2)

(3)

ε0=2Δb/h

(4)

Δb=r-b

(5)

(6)

σ=Eε

(7)

(8)

对应力分布函数(8)在椭圆榫表面进行二重积分，可得到1/4椭圆榫表面的正压力Nnomal，如式(9)所示，简化后得到式(10)。根据椭圆榫表面的对称性，整个椭圆榫上下圆弧表面的正压力大小为Nz，如式(11)所示。由库伦摩擦定律可得到椭圆榫节点摩擦力f，如式(12)所示，而在无胶状态下，节点摩擦力f与榫接合的抗拔力F大小相等，如式(13)所示。

(9)

Nnomal=πELrΔb/(2h)

(10)

Nz=2πELrΔb/h

(11)

f=μNz

(12)

F=2μπELrΔb/h

(13)

式中：r为椭圆榫圆弧部分的半径，即椭圆榫厚度的1/2，mm；Δb为椭圆榫接合过盈量的一半，mm；b为椭圆短半轴长，mm；h为榫头宽度，mm；L为椭圆榫长度，mm。

3 结果与分析

3.1 摩擦系数测量结果

不同正压力及纹理角度下的摩擦系数测量结果如图5所示。对于相同纹理角度的接触对，在不同正压力下摩擦系数基本相同；同时，在同一正压力下，不同纹理角度的摩擦系数也无明显差异。因此，在本研究所采用的加工方式下，不同正压力及纹理角度对木材与木材界面间的摩擦系数并无显著影响。

图5 纹理角度及正压力对摩擦系数的影响Fig. 5 Effects of grain directions and contact forceon friction coefficient

为进一步验证上述结论的准确性，分别测定了各接触面的表面粗糙度，以GB/T 1031—2009《产品几何技术规范(GPS)表面结构轮廓法表面粗糙度参数及其数值》中推荐的轮廓算术平均偏差Ra作为粗糙度的表征值，结果见图6。对6组接触对的9种平面分别进行了测定，结果表明，横纹不同纹理角度和顺纹不同纹理角度下，木材表面的粗糙度均基本相同，证明了摩擦系数试验结果的准确性，即不同纹理角度的横纹与顺纹接触时，摩擦系数均相等。

不同接触面积对摩擦系数的影响结果见图7，接触面积对摩擦系数并无较大影响。在以上平面接触状态研究基础上，进一步测定椭圆榫接触界面的摩擦系数，结果见图8。不同纹理榫接合界面的摩擦系数无较大差异，平均值约为0.54。

图6 不同表面的粗糙度Fig. 6 Roughness of different surfaces

图7 不同接触面积下的摩擦系数Fig. 7 Friction coefficient under different contact areas

图8 不同纹理角度下的摩擦系数Fig. 8 Friction coefficient under different angles

3.2 抗拔力分析

对20个椭圆榫接合的T形试件进行抗拔力测试，结果如图9所示。抗拔力最大值为3 981 N，最小值为2 651 N，平均抗拔力为3 192.5 N，标准差为398 N，此结果也反映出木材力学性能的变异性较大。

图9 抗拔力测定结果Fig. 9 Results of withdrawal force

3.3 榫接合抗拔力数学模型计算结果

通过榫接合节点抗拔力数学模型式(13)，计算本研究所采用的试件抗拔力，试件详细尺寸见图2。其中，榫头宽度方向纹理为径向，参照相关文献[14-15]，采用电测法测得榉木径向的弹性模量为1 374 MPa，代入式(13)中，可得榫头圆弧表面的正压力为5 522.38 N，结合榫接合节点平均摩擦系数0.54，可求得榫头拔出时的最大摩擦力，即榫接合的抗拔力为2 928.08 N。

4 结论与讨论

本研究对木材摩擦特性进行了分析，在此基础之上测定了椭圆榫节点的摩擦系数；之后通过模型假设，建立了榫接合节点抗拔力的数学模型，并与试验结果进行了对比。

在本研究所采用的加工方式下，各接触面纹理角度、接触面积以及接触压力对榫接合摩擦系数无明显影响。这主要是因为通过数控机床加工榫头时，由于进给量小，榫头长度方向需多次切削，两次切削之间会留下微小的接缝，由此形成的接触面粗糙度远大于因纹理造成的差异。因此，不同纹理角度下的榫接合节点摩擦系数无较大差异，节点摩擦系数平均值为0.54。同时，本研究中所建立的模型计算结果与试验结果的最大值和最小值相比均在标准差范围内，且试验结果平均值与模型计算结果的误差为8.3%，但此模型是在一定的假设条件下建立的，这也是造成误差的主要原因。鉴于木材具有较大的变异性，从工程应用角度出发，本研究所建立的数学模型可满足工程计算要求，力学模型计算简单方便，适用于实木榫接合家具结构抗拔力的估算，从而可提高设计效率及产品可靠性。

[ 2 ]钟世禄, 关惠元. 椭圆榫过盈配合量与木材密度的关系[J]. 林业科技开发, 2007, 21(2):57-59. ZHONG S L, GUAN H Y. Relationship between optimal value of interference fit and wood density in oval-tenon joint[J]. China Forestry Science and Technology, 2007, 21(2):57-59.

[ 3 ]TANKUT A N, TANKUT N. The effects of joint forms (shape) and dimensions on the strengths of mortise and tenon joints[J]. Turkish Journal of Agriculture and Forestry, 2005, 29(6):493-498.

[ 4 ]李素瑕, 刘文金, 孙德林. 速生松木家具几种节点接合方式的强度比较研究[J]. 中南林业科技大学学报, 2014, 34(2):122-126. LI S X, LIU W J, SUN D L. Comparative study on corner joints strength of fast-growingPinusmassoninawood furniture[J]. Journal of Central South University of Forestry and Technology, 2014, 34(2):122-126.

[ 5 ]SMARDZEWSKI J. Strength of profile-adhesive joints[J]. Wood Science and Technology, 2002, 36(2):173-183.

[ 6 ]RATNASINGAM J, IORAS F. Effect of adhesive type and glue-line thickness on the fatigue strength of mortise and tenon furniture joints[J]. European Journal of Wood and Wood Products, 2013, 71(6):819-821.

[ 7 ]DERIKVAND M, SMARDZEWSKI J, EBRAHIMI G, et al. Withdrawal force capacity of mortise and loose tenon T-type furniture joints[J]. Turkish Journal of Agriculture and Forestry, 2013, 37(3):377-384.

[ 9 ]张莲洁, 孟庆军, 金维洙, 等. 浅谈国内外木材表面粗糙度的研究现状及发展趋势[J]. 林业机械与木工设备, 2000, 28(6):7-9.

[10]丘湘荣. 木材加工的切削速度对切削现象、切削阻力及摩擦系数的影响[J]. 木工机床, 1986(3):15-22.

[11]SEKI M, TANAKA S, MIKI T, et al. Friction characteristics between metal tool and wood impregnated with phenol formaldehyde (PF) resin during exposure to high pressure[J]. Journal of Wood Science, 2016, 62(3):233-241.

[12]秦理哲, 林兰英, 罗建举, 等. 木材胶合界面性能表征技术研究进展[J]. 世界林业研究, 2013, 26(5):59-63. QIN L Z, LIN L Y, LUO J J, et al. Research progress in characterization techniques of wood bonding interface[J]. World Forestry Research, 2013, 26(5):59-63.

[13]中国林业科学研究院木材工业研究所. 中国主要树种的木材物理力学性质[M]. 北京:中国林业出版社, 1982:10.

[14]王丽宇, 鹿振友，申世杰. 白桦材12个弹性常数的研究[J]. 北京林业大学学报, 2003, 25(6):64-67. WANG L Y, LU Z Y, SHEN S J. Study on twelve elastic constant values ofBetulaplatyphyllaSuk. wood[J]. Journal of Beijing Forestry University, 2003, 25(6):64-67.

[15]DIVOS F, TANAKA T, NAGAO H, et al. Determination of shear modulus on construction size timber[J]. Wood Science and Technology, 1998, 32(6):393-402.

Investigation on withdrawl force of mortise andtenon joint based on friction properties

HU Wengang, GUAN Huiyuan*

(CollegeofFurnishingsandIndustrialDesign,NanjingForestryUniversity,Nanjing210037,China)

The friction properties of oval mortise and tenon joint were investigated by an innovative measuring method. A mathematical model evaluating the withdrawal force of solid wood oval mortise and tenon joint was developed based on reasonable hypothesis. In addition, an experiment was carried out to verify the validity of the mathematical model. The results showed that the effects of the grain directions, contact areas and contact force on the friction coefficient between the mortise and tenon were not significant under the plane contact with the same processing method. The roughness measuring results of each contact surface indicated that the angle had a slight effect on the roughness of longitude and transverse grains, and the roughness was nearly equal under the different angle contact conditions. The friction coefficient of the mortise and tenon joint was measured with variable grain directions by an innovative method. The results were consistent with that of the plane contact and the average friction coefficient was 0.54. In the validation experiments, the withdrawal force of 20 T-shaped specimens joined by oval mortise and tenon were tested, and the average withdrawal force was 3 192.5 N with the standard error of 398 N. By contrast, the result was 2 928.08 N calculated by mathematical model, and the errors were all within the standard deviation compared with the maximum and the minimum values obtained in the experiments. However, the plasticity of wood was not considered, since the interference between mortise and tenon was too weak to lead to the plasticity deformation. As a result, the mathematical model was able to evaluate the withdrawal force of oval mortise and tenon, and provided a foundation for the cohesive force study in the solid wood mortise and tenon joined furniture structure design.

mortise and tenon joint; friction coefficient; withdrawal force; mathematical model

2017-01-10

2017-04-23

国家林业公益性行业科研专项(201204700202)；江苏高校优势学科建设工程资助项目(PAPD)。

胡文刚，男，研究方向为家具设计及理论。通信作者：关惠元，男，教授。E-mail:guanhuiyuan@njfu.com.cn

S781.29

A

2096-1359(2017)04-0158-05