基于直观想象化解不等式成立问题*

福建省惠安第三中学(362100) 江志杰

福建省惠安高级中学(362100) 庄惠平

基于直观想象化解不等式成立问题*

福建省惠安第三中学(362100) 江志杰

福建省惠安高级中学(362100) 庄惠平

含参数的不等式成立问题一直是高考和高三质检的热点素材,题型千变万化、解法精彩纷呈,其中最常规的解法就是分离参数法或构造差函数求最值.然而,对于求解某些含参数的超越不等式成立问题,传统的解法显得繁杂受阻或者抽象费解,难于把握解决问题的关键命脉.为此,笔者拟通过若干高考典例的分析探讨,谈谈数形结合思想在某些不等式成立问题中的展现和运用.

一、转为直线与曲线的位置关系

很多含参数的超越不等式成立问题中,往往蕴含着直线与曲线的位置关系,我们若能从中分离或挖掘出目标函数与特征直线,则从数形结合的角度进行探析,无疑显得更为形象直观、简便快捷!

例1. (2013年全国高考(课标I)理 11)已知函数若|f(x)|≥ax,则a的取值范围是( )

A.(∞,0] B.(−∞,1] C.[2,1] D.[−2,0]

解析本题貌属含参数的不等式恒成立问题,但若用传统的分离参数法或构造差函数求最值,反而更棘手!关键应发现不等式右边是一次函数,研究该不等式恒成立问题,实则分析函数y=|f(x)|的图像与直线y=ax的位置关系(如图1),利用导数知识求得左侧曲线在原点处的切线斜率为−2,依题意得到a∈[−2,0],故答案选D.

例2. (2015年全国新课标I卷理12)设函数f(x)=ex(2x−1)−ax+a,其中a＜1,若存在唯一的整数x0,使得f(x0)＜0,则a的取值范围是( )

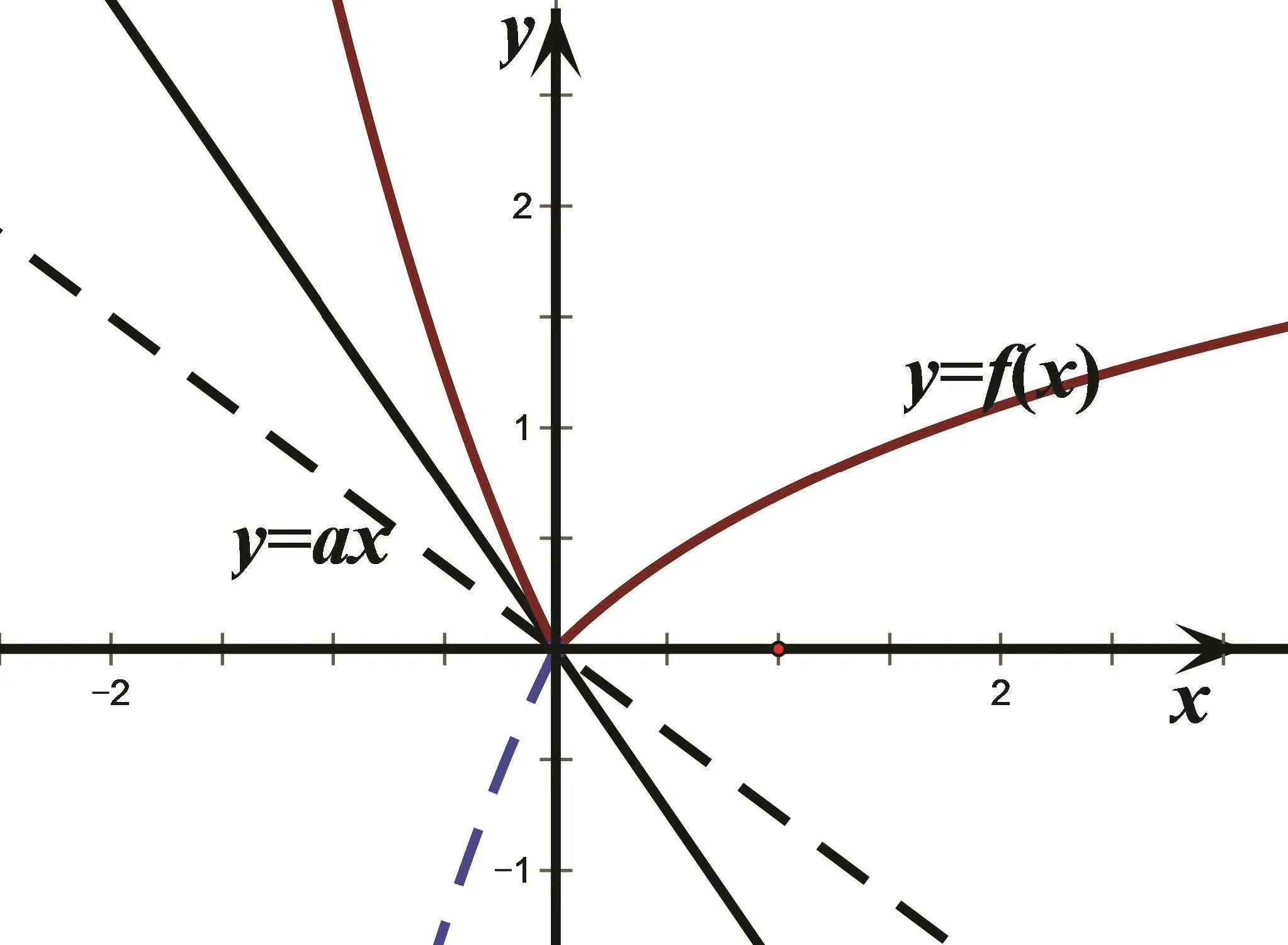
图1

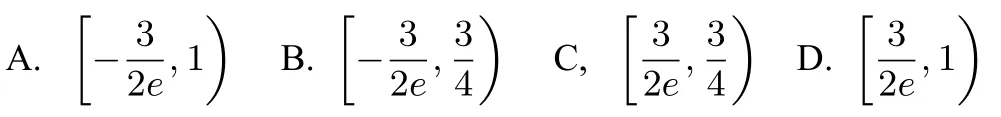
解析解决本题的关键是要注意到:函数f(x)是由超越函数g(x)=ex(2x−1)减去一次函数y=ax−a而成的,其中一次函数y=ax−a=a(x−1)表示绕定点A(1,0)旋转的动直线;超越函数g(x)=ex(2x−1)通过求导得到:g′(x)=ex(2x+1),故函数g(x)在区间上单调递减(且g(x)＜0),g(x)在区间上单调递增.如图2所示.

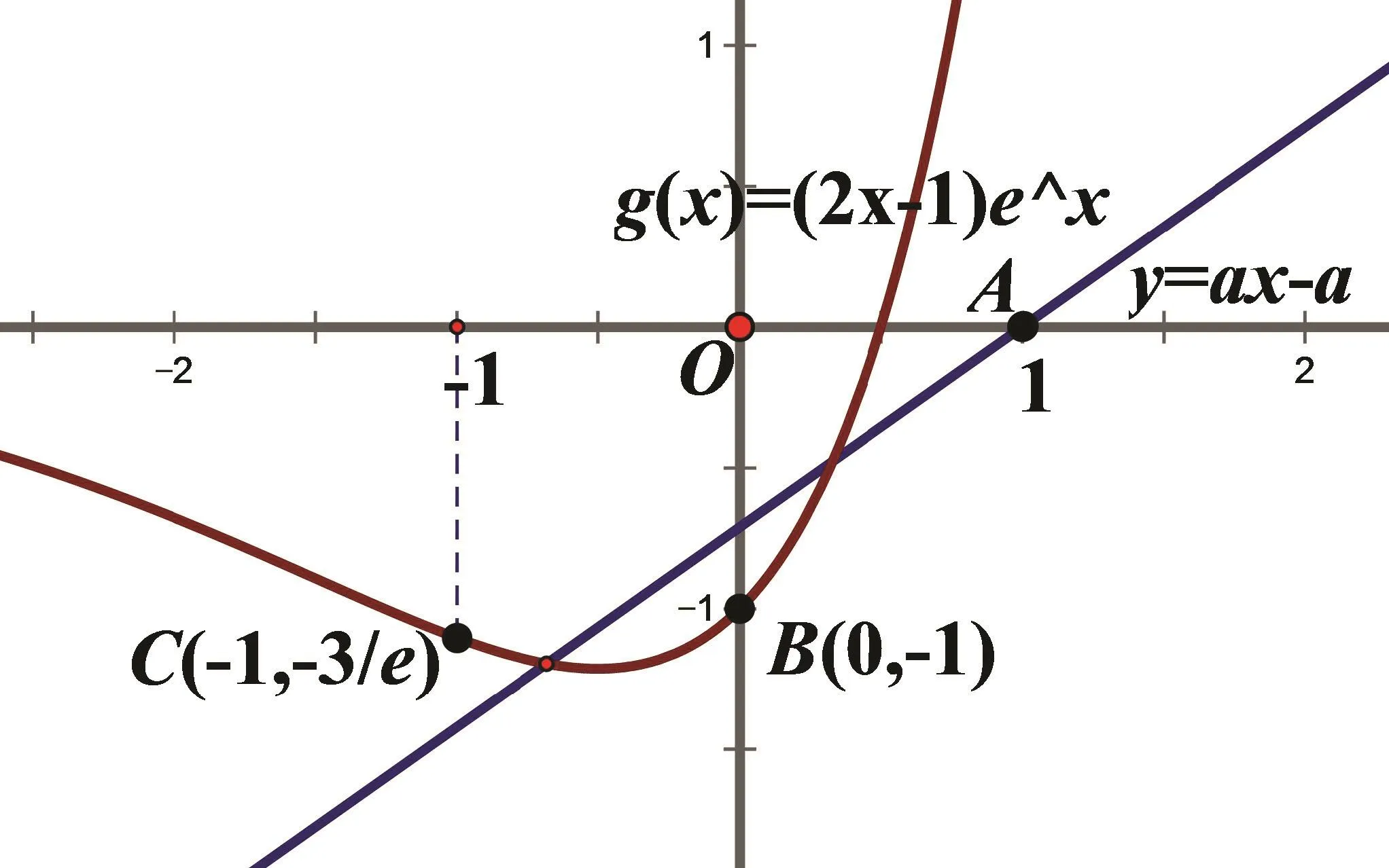
图2

例3.对于函数若存在唯一的正整数x0,使得f(x0)＜0成立,则实数a的取值范围是.

解析本题所提供的含参三次函数模型,极易造成大家企图通过导数工具和对参数a的讨论,去探索该函数的图像特征.然而,对于“存在唯一的正整数x0,使得f(x0)＜0成立”却难以控制!事实上,本题最精妙之处在于发现函数f(x)中隐藏着一次函数模型y=ax+a,即函数f(x)由三次函数减去一次函数y=ax+a而来的,只要控制好直线y=ax+a绕定点A(−1,0)旋转的角度,即可实现问题的化解.

如图3所示,利用导数易得函数g(x)分别在x=2、x=4处取得极大值、极小值,根据题意尝试旋转直线,并比较直线在可能正整数点处的斜率:从而得到

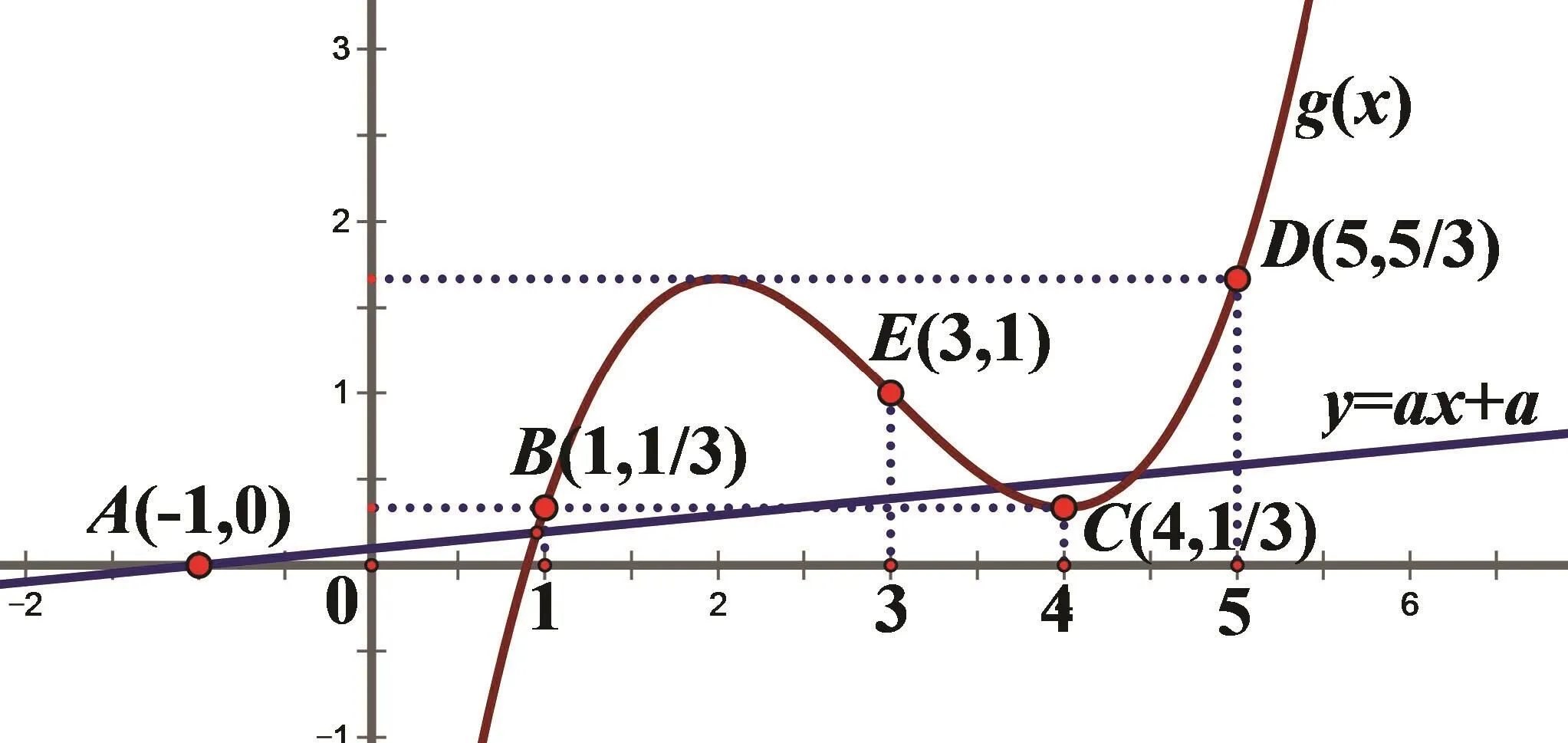
图3

上述思路在不等式成立问题中占据着广泛的应用空间,再如下面一系列问题均可转化为直线与曲线位置关系问题来快捷求解:

(i)(2012年大纲全国理20)设函数f(x)=ax+cosx,x∈[0,π],若f(x)≤1+sinx,求a的取值范围.

(ii)(2012年全国数学联赛福建赛区预赛14)已知函数若x∈[0,2]时,f(x)≥0恒成立,求实数a的取值范围.(答案:a≥1)

(iii)(2010年全国新课标文科卷)设函数f(x)=x(ex−1)−ax2,若当x≥0时都有f(x)≥0,求实数a的取值范围.(答案:a≤1)

(v)(2006年全国II理科卷)设函数f(x)=(x+1)ln(x+1),若对所有的x≥0都有f(x)≥ax.求实数a的取值范围.(答案:a≤1)

二、配凑目标函数的斜率结构

对于能够分离参数的不等式成立问题,很多人还是习惯于优先分离参数,通过求另一端无参函数的最值来确定参数的取值范围,通俗易懂、直截了当!然而这种做法经常碰到的困难是分离参数后的无参函数求导繁杂、难以确定单调区间,造成最值求解受阻.其实,某些经参变分离后的无参函数是具备几何意义的,尤其是很多分式结构的函数蕴藏着“斜率特征”,若能从中挖掘发现,并加以恰当的配凑,也可为解决问题开辟新颖、形象的解法途径!

例4.(2007年全国I理科卷)设函数f(x)=ex−e−x,若对所有的x≥0都有f(x)≥ax.求实数a的取值范围.

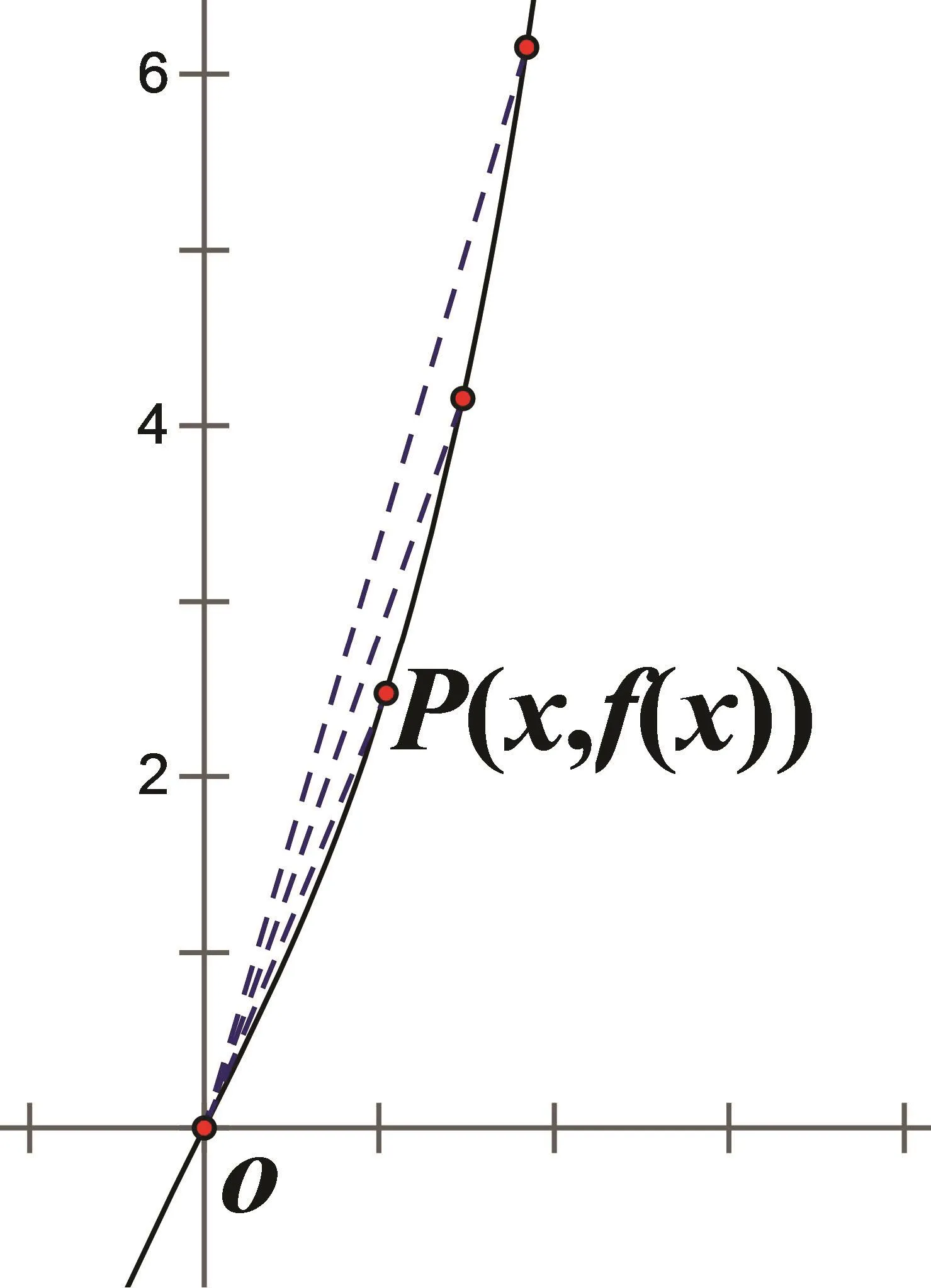
图4

对数函数曲线y=lnx上的两个动点连线斜率小于1−k成立.由y=lnx的图像注意该两动点到x轴的距离相等,且当该距离缩小时两动点连线的斜率变大(如图所示),通过观察容易猜想:

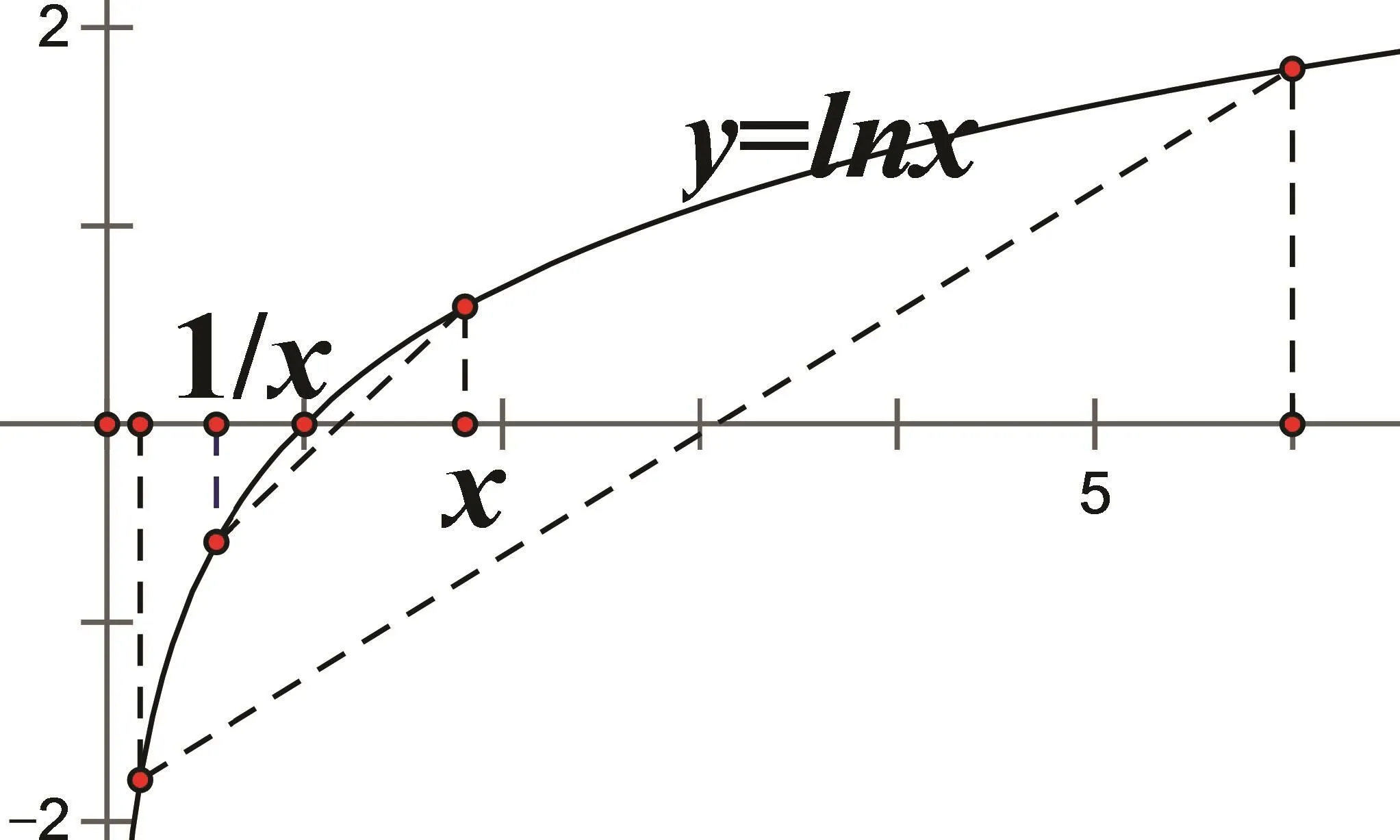
图5

综上,1−k≥1,k≤0.即k的取值范围为(−∞,0].

点评这种经过配凑促使目标函数函数具备斜率意义的做法,其实与前述化为直线和曲线位置关系的做法是一脉相承、彼此交融的,如例4中不等式f(x)≥ax(x≥0)恒成立,也可理解为过原点的直线位于曲线f(x)=ex−e−x下方;再如例5中不等式变形整理得其中若令x2=t,K=1−k,则问题转为:“tlnt＞K(t−1),(t∈(0,1))和同时成立,求K的取值范围”—终究也是直线和曲线位置关系问题.

结束语由上可知,很多含参不等式成立问题的原始背景就是直线与曲线的位置关系,这就让我们清晰地追溯到题目的源泉,站在更高的层面理解不等式问题的本质.并且,我们还可发现:当参数恰为一次项系数时,这个参数往往具备了斜率的几何意义,这就是将不等式转化为直线和曲线位置关系的“核心所在”.

*本文系福建省教育科学“十三五”规划课题《基于数学核心素养的中学主干知识目标定位研究》系列成果之一.