平面向量基本定理应用的几种策略

浙江省江山市清湖高级中学(324100) 康井荣

平面向量基本定理应用的几种策略

浙江省江山市清湖高级中学(324100) 康井荣

纵观近几年的各地高考,经常出现平面向量基本定理应用的向量问题.这类问题一般属于中档题,但很多学生都怕做这种题目,碰到这种问题大多是空白一片.究其原因,是学生对平面向量基本定理理解得不深刻,对等式c=λa+µb中系数λ,µ的含义不清楚,导致对基本定理的处理,缺乏必要的方法和技巧;另外,处理这类问题时往往还需要数形结合,综合运用平面几何知识、解三角形知识、函数知识等加以解决,而学生这方面的综合能力比较欠缺,思维比较单一,使得学生对这种问题心生畏惧,望而却步.

其实这类问题的处理,基本思路是突出数形结合和转化思想,运用平面几何知识和向量的运算性质,化向量运算为纯代数运算或几何运算,归纳起来,大致有以下六种转化策略:

1.将向量分解,转化为平面几何问题

平面向量基本定理实质就是向量的合成与分解.因此,将向量c沿基底a,b进行分解,结合已知条件和平面图形的几何性质,可以较快的找到λ,µ的关系.

2.利用向量相等的充要条件转化为关于λ,µ的方程(组)解决

具体地说,就是根据已知条件c=λa+µb,结合图形,用另一种方法将c用基底a,b线性表示,即将c写成c=ma+nb,然后比较系数得到λ=m,µ=n的方程(组).

3.两边点乘向量转化为纯代数运算

由于向量的数量积是一个数量,因此,对等式c=λa+µb两边点乘向量a、b或c,也可以将其转化为纯代数运算.

4.通过两边平方,化向量为纯代数运算

由于向量的模和平方都是数量,因此在等式c=λa+µb中,如果已知a,b的模或者它们夹角,可以通过两边平方转化为纯代数运算.

例4(2015年杭州二中高考仿真模拟题第16题)在△ABC中,∠B=60°,O为△ABC的外心,P为劣弧AC上的一动点,且则x+y的取值范围为____.

分析由于向量的模相等,且的夹角也确定,因此可以考虑两边平方转化为代数不等式问题.

5.利用坐标运算将向量问题转化为纯代数问题

由于向量的坐标运算也是纯代数运算,因此通过建系设点,利用向量的坐标运算解决c=λa+µb的问题也是一种转化的策略.

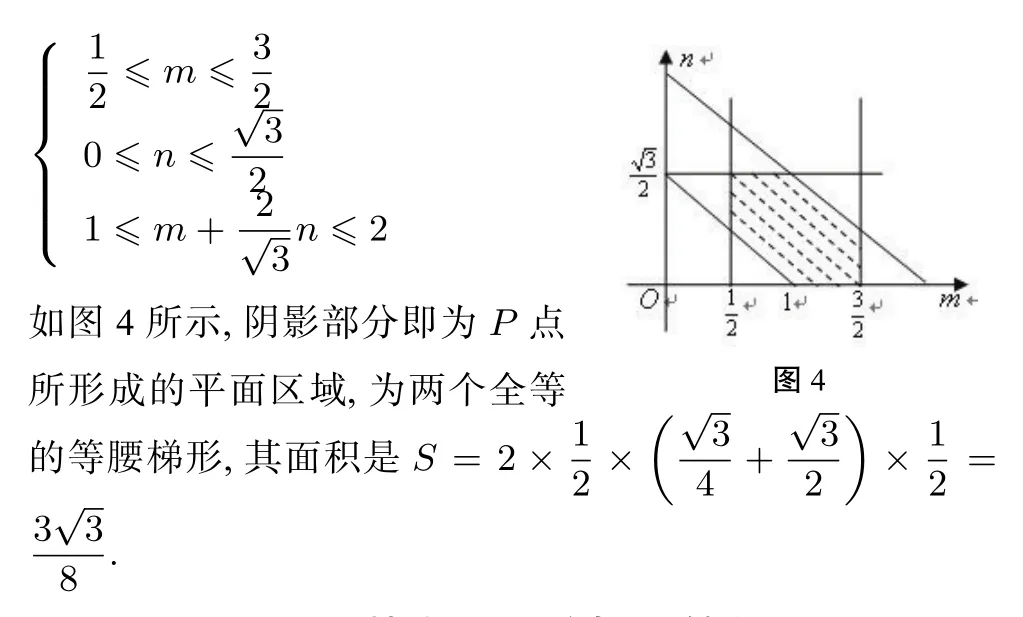
分析要求出动点P所形成的平面区域的面积,必须探求动点P所形成的平面图形,为此我们可以通过建立坐标系,设出P点的坐标(m,n),再根据已知条件找到m,n所满足的条件,这样就将向量问题转化为线性规划的问题了.

6、利用平面向量基本定理的推论转化为平面几何问题

(1)平面向量基本定理的推论是指:设平面内有三点P、A、B,且若满足λ+µ=1,则P、A、B三点共线,反之也成立.解题时,如果能将已知条件转化为λ+µ=1,就可以根据这个结论确定c的终点位置,利用平面几何知识快速解题.

分析如果将λ+2µ=2变换成再将OA延长一倍,那么就将条件转化为λ′+µ′=1了,这样就可以根据P点的位置快速求出投影的取值范围.

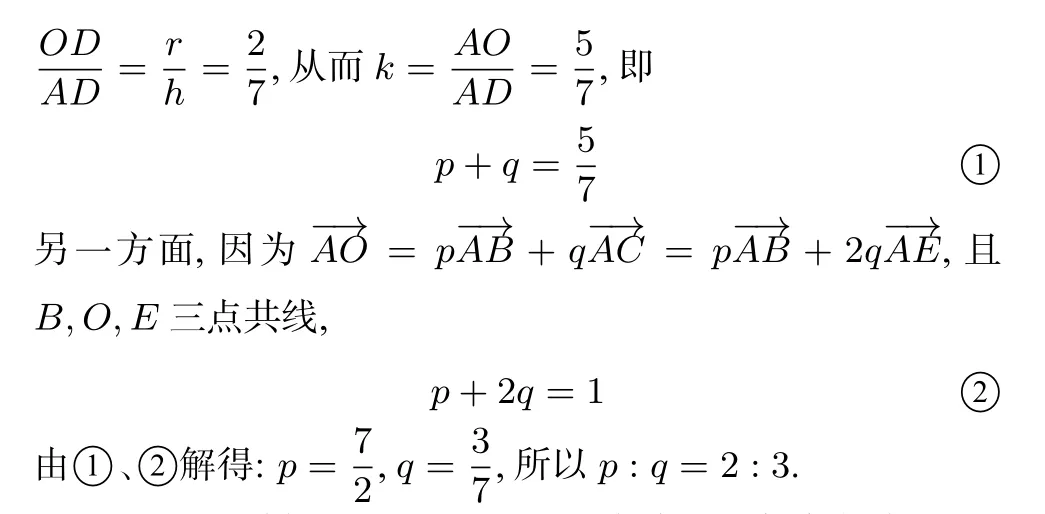
小结深刻理解平面向量基本定理,牢牢抓住c=λa+µb转化的基本思想,结合图形和向量的运算性质,在解题过程中就会显得游刃有余.同学们在平时解题中只要善于多思考,多总结,那么一切困难都可以迎刃而解.运用基本定理的推论,可以使解题更快捷简便,前面的例4、例5两个例题,都可以采用这个结论解决,读者不妨一试!

[1]杨雪.一类向量线性和的系数问题解决方案的探究[J].中学教研,2014(9):33-36.

[2]高贺清.利用三点共线巧解一类向量系数问题[J].中学生数理化,2012(11):20-20.