激波汇聚效应对球形气泡演化影响的数值研究∗

梁煜 关奔 翟志刚 罗喜胜

(中国科学技术大学近代力学系,合肥 230027)

(2016年10月7日收到;2016年10月25日收到修改稿)

激波汇聚效应对球形气泡演化影响的数值研究∗

梁煜 关奔 翟志刚†罗喜胜

(中国科学技术大学近代力学系,合肥 230027)

(2016年10月7日收到;2016年10月25日收到修改稿)

利用三维程序,对比研究了汇聚激波及平面激波冲击下SF6球形气泡演化规律的异同,以期发现激波的汇聚效应对界面演化的影响.三维程序采用多组分可压缩欧拉方程,基于有限体积法,利用MUSCL-Hancock格式进行数值求解,可以达到时间和空间的二阶精度.相比平面激波,汇聚激波由于存在曲率,且激波强度以及壁面效应在汇聚激波运行的过程中逐渐增强,使得激波冲击后的流场演化有较大的不同.计算结果表明:汇聚激波作用下,气泡界面的涡结构更加尖锐;气泡内部的透射激波聚焦程度更强,在界面下游附近形成的最高压力大于平面激波算例,由此产生的射流运动速度更快;由于汇聚激波曲率及激波强度的变化,导致界面上涡量的分布规律以及涡量幅值产生较大变化.通过界面上产生的环量以及界面内外气体混合速度的对比表明,汇聚激波更有助于涡量的产生以及气体的混合.因此激波的汇聚效应对气泡界面演化具有重要影响.

汇聚激波,球形气泡,三维,数值模拟

1 引 言

在研究激波加速的不均匀流动中,激波-气泡相互作用(SBI)是一项基本的研究课题,球形界面作为最基本的界面结构得到了大量的研究[1].SBI是一个复杂的过程,在界面处会出现激波折射、反射以及衍射等物理现象,而且气泡内外的气体属性也影响着波系结构的发展形式.Rudinger和Somers[2]最早研究了激波作用下球形和柱形界面的不稳定性发展问题,得到了界面演化的图像并提出了一种简单的、可以预测界面速度的模型.Haas和Sturtevant[3]进行了平面弱激波与球形界面、柱形界面相互作用的实验研究,通过放射性照相技术,记录了气泡迅速弯曲变形直至破裂的整个过程,并首次指出激波作用下轻气泡和重气泡分别会在不同阶段出现双涡环结构和气泡射流结构. Layes等[4]运用阴影技术并结合高速摄相机获得了平面激波作用下重气泡、轻气泡以及密度接近环境气体的气泡界面演化的全过程图像,展示了不同气体球形界面的变形差异,并对气泡演化中涉及的一些特征尺寸进行了定量的分析和归纳.Si等[5]采用高速纹影法,开展了平面激波及其反射激波作用下球形气体界面演化的研究,结果表明不同反射距离下界面不稳定性的发展是不同的,同时也表明压力扰动机制和斜压机制是导致界面不稳定性发展的主要原因.数值方面,W inkler等[6]研究了马赫数为2.0的平面激波与R22气泡相互作用的算例,发现波后流场中有超声速涡环的出现.Niederhaus等[7]利用RAPTOR求解器(网格自适应的二阶精度的Eulerian-Godunov代码)通过改变激波马赫数和气体组分,进行了一系列的激波-气泡相互作用的数值模拟研究,分析了不同算例中的界面压缩率和环量变化,并基于一维理论模型提出了环量计算模型.Zhu等[8]利用大涡模拟方法对激波冲击轻气泡过程中的涡环进行了研究,分析了入射激波强度和方位角对涡环的形成和发展造成的影响.Zhai等[9]采用VAS2D(2-dimensional and axisymmetric vectorized adaptive solver)方法数值模拟了平面入射激波分别与两种不同组分的重气泡相互作用的过程,着重分析了不同声阻抗和激波强度对射流的形成和发展产生的影响.沙莎等[10,11]通过大涡模拟方法对Si等[5]的实验进行了三维数值模拟,并分析了不同反射距离下气泡内高压区的形成对射流产生的影响.

之前的研究主要集中于平面激波情况,对于激波马赫数不断变化并且具有一定曲率的汇聚激波的研究较少.在很多实际问题中,如惯性约束核聚变问题[12,13],入射激波并非简单的平面形状.然而在实验室条件下产生一个形状可控、具有平滑曲率的汇聚激波仍是一个难题,汇聚激波诱导下界面不稳定性的研究更是少之又少,因此研究汇聚激波作用下的界面不稳定性具有重要的应用价值.汇聚激波与界面的相互作用也带来许多新的科学问题:几何收缩带来的Bell-Plesset[14,15]效应,非均匀气流带来的Rayleigh-Taylor[16,17]效应,多次反射带来的强压缩性等,因此对其开展深入研究也具有十分重要的学术意义.Zhai等[18]基于激波动力学方法生成柱形汇聚激波,并由王显圣等[19]通过实验详细分析了柱形汇聚激波及其反射激波与SF6球形气泡相互作用的全过程.Si等[20,21]通过对汇聚激波与SF6气柱、SF6气泡相互作用的实验分析,指出激波强度以及激波和气泡界面的初始形状决定了气泡特征长度的增长和斜压涡量的分布.杨伟航和罗喜胜[22]采用VAS2D方法数值模拟了柱形汇聚激波冲击SF6气柱的算例,并和平面激波冲击SF6气柱的算例做对比,分析了不同算例中的壁面反射波对界面演化的影响和计算域内环量的变化,结果表明激波的汇聚效应对二维气柱界面的演化形态以及流场的定量特征有重要的影响.由于VAS2D是二维程序,还不足以对三维气泡演化进行模拟.实验结果[20,21]表明,球形气泡在汇聚激波与平面激波诱导下的演化规律有着较大的区别,但由于实验技术的限制,难以定量比较汇聚激波与平面激波诱导界面演化的差异.在VAS2D二维程序的基础上,本文开发了一套三维程序,计算了汇聚激波作用下SF6气泡的演化过程,并与平面激波作用下SF6气泡界面演化规律进行了定性的对比.此外,通过界面下游处形成的最高压力、界面射流结构特征长度以及气泡内外气体混合程度等物理量,定量地讨论了激波的汇聚效应对界面演化的影响.

2 数值方法

本文利用三维程序对激波-气泡相互作用问题进行数值模拟,均不考虑化学反应,忽略气体黏性影响,采用多组分可压缩欧拉方程对流场演化进行求解,控制方程为

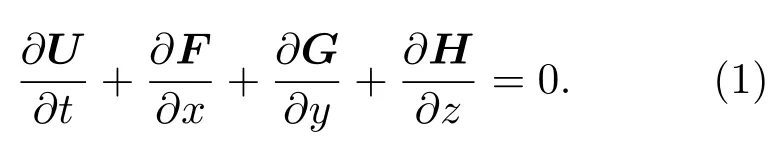
这里,U是守恒变量,F,G和H分别代表x,y和z方向的流通量,可以写成如下形式:

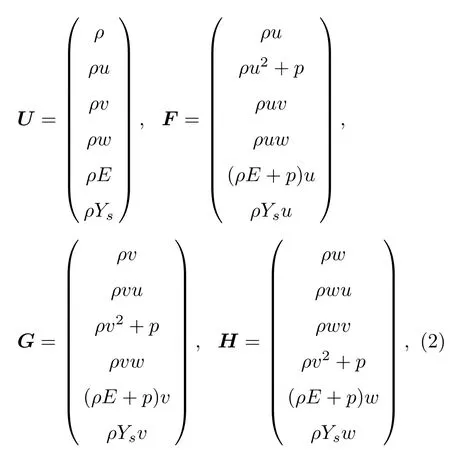
其中,p,ρ,E,u,v,w分别表示界面两侧气体混合物的压力、密度、单位质量的总能以及x,y,z方向的速度分量;Ys表示界面一侧的气体s在混合物中所占的质量分数,界面另外一侧气体 a的质量分数为Ya=1−Ys.混合物的状态方程可以表示为p=ρT(YsRs+YaRa),其中Rs和Ra表示气体s和气体a的气体常数,T表示混合物的温度;混合物的总能E=Yses+Yaea+(u2+v2+w2)/2,其中es和ea为界面两侧气体的比内能.

本文采用三维程序对上述方程进行求解,该程序基于有限体积法,利用MUSCL-Hancock格式对欧拉方程进行数值求解,计算程序可以达到时间和空间的二阶精度,并通过HLLC(Harten-Lax-van Leer C)格式对网格面上的通量进行求解.另外,程序采用由Gambit软件生成的非结构六面体网格作为计算网格,数据结构为cell-face型.最后,程序采用MPI并行计算的方法,突破了单机计算的内存上限,提高了计算效率.

为了验证数值方法的可靠性,本文首先根据Zhai等[23]的平面激波与SF6气泡相互作用的实验进行数值模拟.计算采用了与实验相同的参数,包括设置初始激波马赫数为1.23,气泡半径为15mm,气泡内部SF6体积分数为90.85%.首先对程序进行了网格收敛性验证,本文采用气泡半径上分布60,75,90,105和120个网格分别计算了平面激波与气泡作用25µs时刻气泡中轴线上的压力分布,如图1所示,结果表明网格收敛性较好.为减小计算量,本文采用半径上105个网格对上述算例进行数值模拟,并和实验结果进行了对比,如图2所示,可以看到数值结果和实验结果定性吻合.

定量地,我们对比了气泡的特征结构(长度和高度)尺寸随时间的变化,如图3所示,其中以气泡水平方向的直径D0作为特征长度.由图3可见数值计算中的气泡界面结构的演化与实验结果符合较好.高度Hu/D0的变化实验值要比计算值稍大,这是由于SF6气泡密度较大,实验中形成的气泡并非完美的球形,而是椭球形,在竖直方向上的直径要大于水平方向的直径,而特征长度均采用水平方向的直径导致的.由此可以看出,本文的三维程序在模拟平面激波与气泡相互作用的算例中具有较好的适用性.

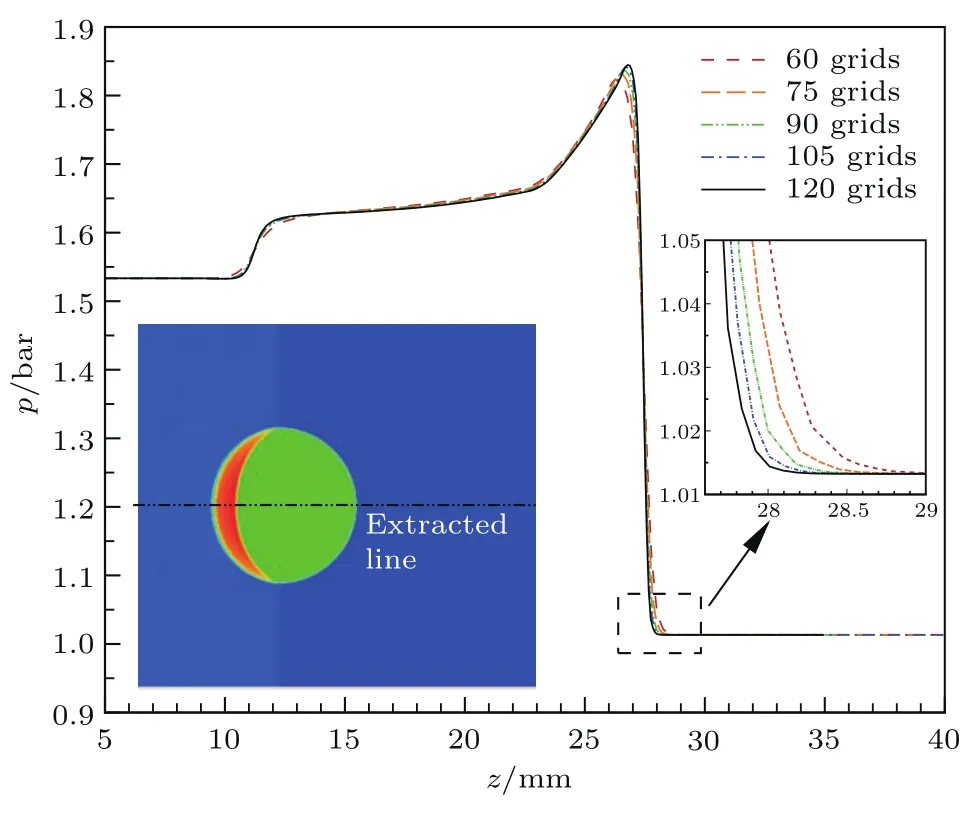
图1 (网刊彩色)不同计算网格下,SF6气泡对称轴处压力的变化(1 bar=105Pa)Fig.1.(color on line)The p ressure profi les w ith different grids along the horizontal symm etry axis of the SF6bubb le im pacted by a p lanar shock wave (1 bar=105Pa).

图2 平面激波冲击下SF6气泡演化的实验结果(上)与数值结果(下)的对比Fig.2.Com parison of experim ental(upper)and num erical(lower)sch lieren im ages of an SF6gas bubb le accelerated by a p lanar shock wave.

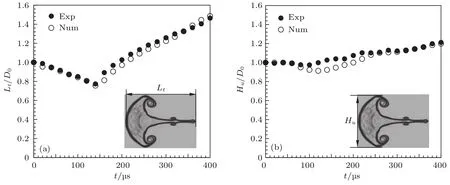
图3 平面激波冲击下SF6气泡特征长度随时间演化关系 (a)界面长度Lt;(b)界面高度HuFig.3.T im e evolution of the SF6interface structu res im pacted by a p lanar shock wave:(a)The interface length Lt;(b)the interface height Hu.

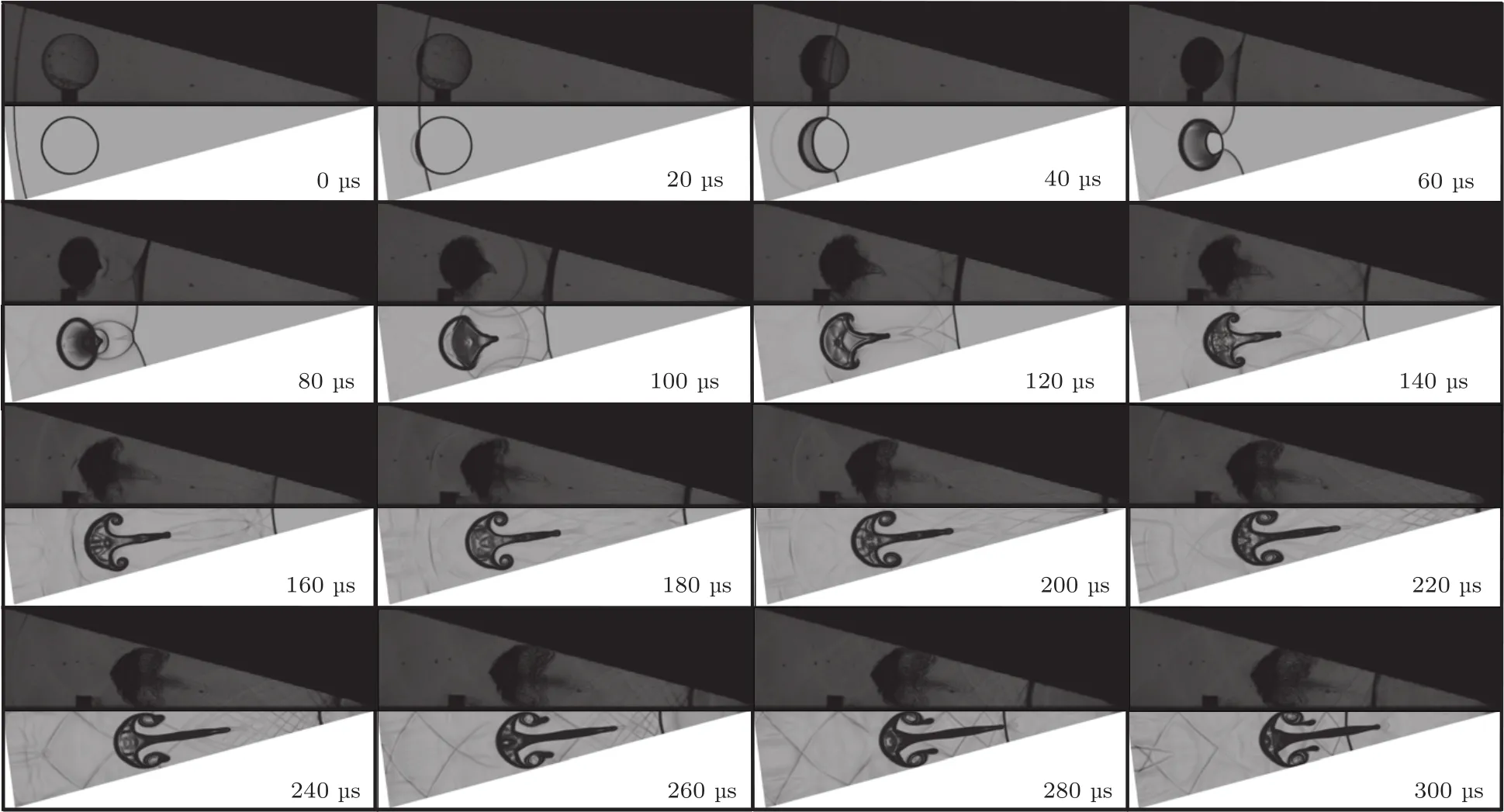
图4 汇聚激波冲击下SF6球形界面演化的实验结果(上)和数值结果(下)的对比Fig.4.Com parison of experim ental(upper)and num erical(lower)sch lieren im ages of an SF6gas bubb le accelerated by a cy lind rical converging shock wave.

此外,本文数值模拟了柱形汇聚激波与SF6气泡相互作用的过程,并与已有的实验结果[14]进行了对比,如图4所示.在图中t=0µs时刻,汇聚激波的马赫数为1.3,距离汇聚中心102.5 mm,气泡半径为8 mm,气泡中心到汇聚中心的距离为87.5 mm.另外,在数值计算中气泡内部SF6体积分数为62%,其余为空气,外界为纯空气,环境温度为298 K,计算中初始时刻汇聚激波波后采用均匀流场.可以看到在入射阶段,无论是波系结构还是界面形态,数值结果和实验结果均吻合较好.但在反射阶段,数值计算中的反射激波速度要明显大于实验中反射激波的速度,此外实验中的射流结构在反射激波到来之前几乎消散,而计算中未出现类似现象.这些差异可能是由于数值方法忽略粘性和热传导效应导致的.此外,我们对比了反射激波再次作用于界面之前的界面特征长度的变化,如图5所示,可以发现计算结果与实验结果符合较好.

以上定性和定量的对比充分说明本文的三维程序在模拟平面激波或汇聚激波冲击球形气泡的算例是可靠的.由于以上两种工况的初始条件差异较大,无法说明平面激波和汇聚激波冲击球形界面的差异.在接下来的工作中,我们采用前文中的数值方法分别模拟了平面激波和汇聚激波冲击球形界面的算例,采用了除激波曲率之外的相同初始条件,以说明激波的汇聚效应对球形气泡界面发展的影响.

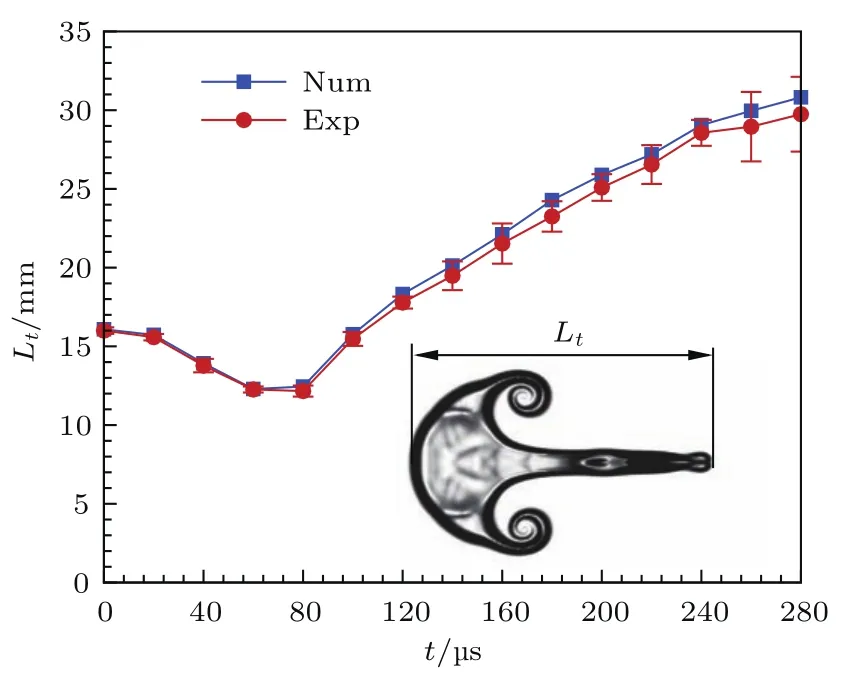
图5 (网刊彩色)汇聚激波作用下SF6球形气泡特征长度随时间演化关系Fig.5.(color online)Evolution of the characteristic length of the SF6gas bubb le accelerated by a cy lind rical converging shock wave.

3 汇聚激波和平面激波与球形气泡相互作用

3.1 计算模型

本文涉及的两个算例的计算区域如图6所示,计算区域横向长度(z方向)均为105 mm,高度(y方向)为28mm,宽度(x方向)为24mm.气泡半径均为8mm,气泡内部气体为纯SF6,环境气体为纯空气,环境温度为298 K,压强为一个大气压.入射激波距离汇聚中心或者平面反射固壁94.2 mm,气泡中心的初始位置与汇聚中心或固壁边界的距离均为85.7 mm,区域的左边界均采用开口条件,右边界和上下边界均采用固壁条件.初始激波马赫数(即距离界面中心8.5mm处的激波马赫数)为1.30,波后均采用均匀流场.对于汇聚激波算例,汇聚角度为15◦.两个算例的不同之处一是汇聚激波强度及曲率的变化,二是壁面效应不同.

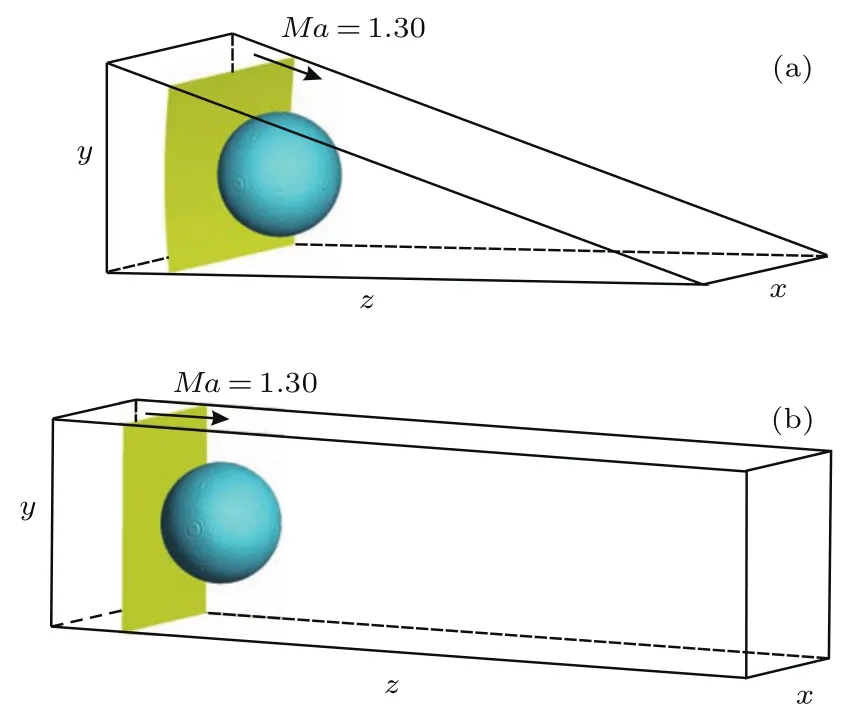
图6 (网刊彩色)激波与气泡相互作用初始时刻图 (a)汇聚激波条件;(b)平面激波条件Fig.6.(color online)The initial state of a spherical gas bubb le accelerated(a)by a cylind rical converging shock wave and(b)by a p lanar shock wave.

3.2 气泡界面形态演化对比

汇聚激波和平面激波分别与球形气泡作用后的界面演化纹影如图7所示.由于汇聚激波强度逐渐增大,导致界面受到更强的压缩,界面内部密度增大较明显(t=50µs,两种工况下界面处理方式相同).可以看到汇聚激波与平面激波作用下的界面演化有一定的相似性,比如激波穿过气泡的过程中,由于斜压项产生的涡量诱导界面不断发生变形,气泡不断卷起并且逐渐产生两个反向旋转的涡结构,但涡结构的形态有一定的区别.在平面激波条件下,界面上产生的涡结构的边缘比较圆滑;而汇聚激波条件下涡结构的边缘却是扁平并且尖锐的(t=150—200µs).其原因可能有两个:一方面,由于汇聚激波的强度在传播过程中逐渐增大,导致压力梯度的增大和流场中压力分布的不均衡,产生的涡量也就更多,导致涡结构与界面主体的运动速度的差距相比平面激波更大;另一方面,在汇聚激波条件下,界面越向汇聚中心运动,空间越小,壁面影响越明显,因此涡结构变得更加扁平和尖锐.其次,我们可以看到,汇聚激波条件下射流部分的密度不断变化,并且和界面主体相连的区域逐渐加粗(t=200—250µs).这是因为汇聚激波条件下的界面主体部分不断转化为射流与界面主体相连的根部结构,因此界面主体部分在减小,界面主体和射流的密度不断变化.此外,汇聚段中激波的相互作用和干扰使流场中的波系结构比平面激波情况更加复杂,特别是当汇聚激波条件下的反射激波再次作用于界面上时,会使其更早地进入湍流混合阶段(t=350µs).

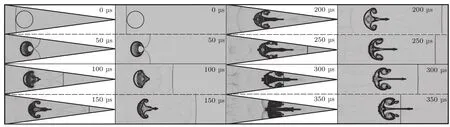
图7 汇聚激波(左)和平面激波(右)条件下SF6气泡界面演化纹影图Fig.7. Sch lieren im ages of of a spherical gas interface im pacted by a cy lind rical converging shock wave (left)and by a p lanar shock wave(right).

3.3 射流形成时刻压力分布对比

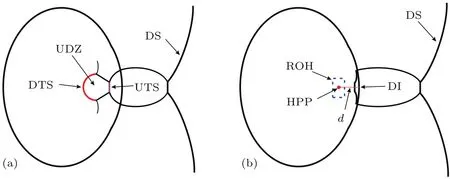
图8 (网刊彩色)激波聚焦前后波系示意图 (a)激波聚焦之前;(b)激波聚焦之后;其中,DS为绕射激波;DTS为向下游运动的透射激波;UTS为向上游运动的透射激波;ROH为高压区;HPP为最高压力点;D I为下游界面; UDZ为未受扰动的区域;d为最高压力点与下游界面的距离Fig.8.(color on line)Schem atics of wave patterns shortly before and after shock-focusing:(a)Before shock focusing;(b)after shock focusing.DS,d iff racted shock;DTS,transm itted shock m oving downward;UTS, transm itted shock m oving upward;ROH,region of high pressure;HPP,the highest pressure point;DI, dow nstream interface;UDZ,undisturbed zone;d,distance from HPP to downstream pole.

在激波作用于SF6气泡后,射流结构是一个有趣的现象.Zhai等[9,23]的相关研究表明,射流的产生与透射激波在气泡内汇聚产生的高压有关.为了进一步说明激波的汇聚效应对射流结构产生的影响,本文对下游界面即将产生射流结构时刻的压力分布进行对比.汇聚激波或者平面激波与气泡相互作用后,内部的透射激波发生聚焦,透射激波的两端在气泡内部的下游界面附近发生相交,产生了向上游运动的激波,激波聚焦之前气泡内外的波系如图8(a)所示.随着时间的推进,向上游运动的激波和向下游运动的透射激波的中心部分在下游界面附近相遇,激波相交后的波系结构如图8(b)所示,产生的高压区会诱导射流的产生.一般来说,最高压力的幅值以及最高压力区到下游界面的距离是影响射流速度和射流尺寸的两个重要因素.计算结果表明,汇聚激波算例的最高压力点距离下游界面1.495 mm,相应的平面激波算例的最高压力点距离下游界面1.470 mm.在汇聚激波条件下,气泡内的透射激波以及空气中的入射(绕射)激波运动速度都是逐渐增大的,但由于空气中的声速较大,相对而言,入射(绕射)激波运动速度的增幅要大于透射激波运动速度的增幅.因此入射(绕射)激波较早地在下游极值点处相遇,导致界面内部向上游运动的激波产生也较早,该道激波需要向上游移动较大的距离才能与透射激波发生激波-激波干扰.因此,在汇聚激波条件下,激波-激波干扰发生的位置较平面激波条件更远离下游界面,形成的最高压力区距离下游界面也就更远.仅从这一点来说,如果平面激波条件下和汇聚激波条件下在激波-激波干扰时产生的压力类似,那么在平面激波条件下由高压诱导的射流结构应该较明显.由图7我们可以看到汇聚激波条件下的射流结构更加明显,因此我们有理由相信激波-激波干扰在两种工况下产生的压力峰值并不相同,而且是汇聚激波条件下产生的压力更高.为此我们从数值结果中提取了气泡中轴线上沿三个坐标轴方向的压力分布,如图9所示.可以看到,汇聚激波条件下达到的最高压力更高,达到61.48 bar,平面激波条件下达到47.38 bar,比值为1.30.同时,我们计算了在没有气泡界面的情况下,汇聚激波和平面激波扫过上述最高压力点的波后压力分别为1.93 bar和1.84 bar,比值为1.05,可见汇聚激波和平面激波在气泡内部的聚焦程度不同.另外,汇聚激波条件下波后高压区域的压力值相比平面激波条件在沿z方向和x方向更大,但在y方向远离聚焦点的区域上压力差别不大.这是由于汇聚激波拥有更强的能量,会在气泡的下游界面附近出现更强的激波聚焦现象.另外,汇聚激波在气泡内部从各个方向聚焦的过程中,由于其曲率更接近气泡,因此沿着z方向和x方向的波后压力更大.但y方向的压力主要受气泡中间剖面上的汇聚激波影响,而在中间剖面上两个算例的的波后压力相差不大,因此汇聚激波条件下y方向的的压力仅在聚焦点附近更大.

3.4 气泡界面极点位置对比

为了说明激波的汇聚效应以及波后的非定常流场对界面特征点速度的影响,本文统计得到了SF6气泡界面上游和下游极点位置随时间的变化,如图10(a)所示,其中(R−r)表示界面极点位置与初始时刻上游界面极点位置的距离.对于上游界面而言,当汇聚激波或平面激波作用界面之后,两种工况下上游极点均向下游运动,且在反射激波作用之前,二者的运动速度十分接近.在汇聚激波条件下,由于汇聚激波在传播过程中强度逐渐增大,波后气流速度加大,因此界面运动速度增大;与此同时,激波汇聚过程中波后压力不断升高,从而又抑制了界面速度的进一步提升.而且在汇聚激波波后会出现许多反射压缩波,这些反射压缩波会多次作用在界面上,同样也会在一定程度上抑制上游界面向下游运动.综合这些因素,在本文研究的工况下,汇聚激波并没有对上游界面的运动速度产生较大的影响.

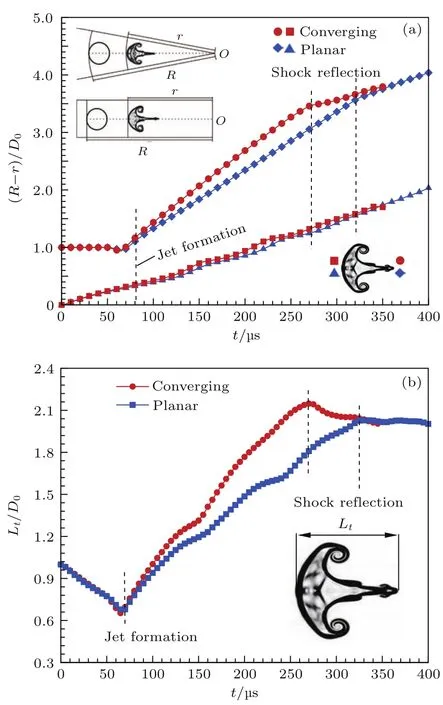
图10 (网刊彩色)平面激波和汇聚激波冲击下SF6气泡界面特征点和特征长度变化 (a)界面上下游极点位置; (b)界面长度Fig.10.(color on line)Com parison of the evolu tion of an SF6gas bubb le im pacted by p lanar and converging shock waves:(a)D isp lacem ents of upstream and dow nstream poles;(b)interface length.

在射流形成之后,我们可以看到汇聚激波条件下的射流移动速度明显高于平面激波条件.从最高压力分布的分析得知,汇聚激波条件下在中轴线上形成的最高压与界面外的压力差高于平面激波算例,因此在中心处高压区的驱动下,汇聚激波条件下形成的射流运动速度更大.在反射激波到来之前,可以看到射流的运动速度是逐渐减缓的,这主要是因为随着射流向汇聚中心运动,汇聚激波诱导的波后压力逐渐升高,抑制了射流的加速运动.当反射激波作用于射流时,相比平面激波条件,汇聚激波条件下反射激波的冲击作用更加明显,表现为射流速度减小的幅度更大.这主要是因为当反射激波作用于射流头部时,汇聚激波条件下的反射激波强度更大,诱导的反向气流速度更大以及反射激波波后压力更大引起的.因此,在如图10(b)所示的气泡中轴线上特征长度Lt的对比中,射流形成后汇聚激波算例的增长速度明显高于平面激波算例.最后,当反射激波作用于界面之后,汇聚激波条件下射流速度减小的程度高于平面激波条件.

3.5 气泡界面环量对比

涡量的产生与分布是界面不稳定性发展的一个主导因素,涡量的产生主要来源于压力梯度和密度梯度的不重合.压力梯度主要来源于激波,密度梯度主要来源于不同密度流体界面.由于汇聚激波在运动过程中强度不断增强,而且激波面存在一定的曲率,这在一定程度上会导致斜压涡量幅度大小的变化.为了说明激波的汇聚效应以及激波的曲率效应对涡量产生的影响,本文给出了气泡界面下半平面环量随时间的变化,如图11所示.其中, Converging,Converging+和Converging−分别是汇聚激波条件下界面上的总环量、正环量和负环量; Planar,Planar+和Planar−分别是平面激波条件下界面上的总环量、正环量和负环量.数值模拟中环量Γ的表达式如下:

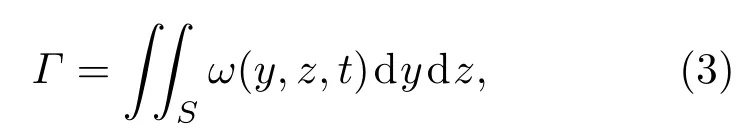
其中,S是界面的计算区域,ω是界面上局部微元的涡量,d y和d z分别是微元在y方向和z方向上的尺寸.从图11可以看到,在入射激波与气泡相互作用的过程中,斜压机制均导致两种工况下总环量的不断上升.

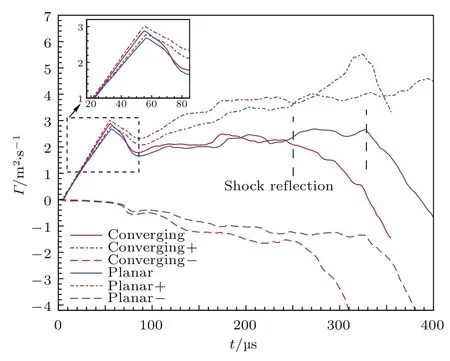
图11 (网刊彩色)汇聚激波和平面激波条件下x方向环量统计图Fig.11.(color on line)Com parison of circu lation in x d irection under converging shock and p lanar shock.

对于平面激波冲击气泡而言,当激波接触界面上游极值点A处到激波运动到界面最高点C的时间内,由入射激波引起的压力梯度大小和方向都不变(只考虑规则折射的情况),密度梯度大小不变,方向改变,如图12(a)所示,使得在上游界面涡量的产生呈正弦分布,在A处涡量为零,在C处涡量幅度达到最大值.对于汇聚激波而言,压力梯度和密度梯度之间的夹角从开始的180◦逐渐减小到C处的90◦.只是由于汇聚激波曲率的变化,这里的C点应该在最高点下游某处(与平面激波相比,密度梯度和压力梯度夹角相同时,汇聚激波更靠近下游),如图12(b)所示.由于汇聚激波强度不断增大,诱导的压力梯度不断增大,因此,汇聚激波条件下在前期产生的涡量幅度稍大于平面激波条件.在激波从C处运动到界面下游极值点B处的过程中,产生的绕射激波波面几乎始终保持与界面的正交.也就是说在这个过程中,压力梯度和密度梯度的方向虽然都在变,但二者之间的夹角不变,而且始终是正交,只有压力梯度的大小随着绕射激波强度的减弱而变小.由于绕射激波的强度是呈指数衰减的,因此波后的压力应该是按指数平方的规律衰减的.总的来说,平面激波作用在界面上引起的涡量变化为:在上游界面涡量幅值从界面极值处的零值按照正弦函数的变化规律增大到界面最高点处的极大值;然后在下游界面,涡量又从极大值衰减至界面极值点B处的零值.A点的涡量为零是由于斜压性为零,而B点的斜压性并不为零,而是两侧的绕射激波均相交于B点,二者引起的涡量大小相等,方向相反,从而B点的涡量也为零.当绕射激波在下游极值点处相遇之后,主激波离开界面,界面上累积的涡量会达到一个极大值.对于汇聚激波而言,激波绕射阶段,强度同样衰减,压力梯度和密度梯度同样始终保持正交,不同的是,汇聚情况下绕射激波强度一方面呈指数规律衰减,另一方面又由于汇聚而增大.因此,在激波直接作用于界面的过程中,汇聚激波条件下产生的涡量幅度要大于平面激波条件.

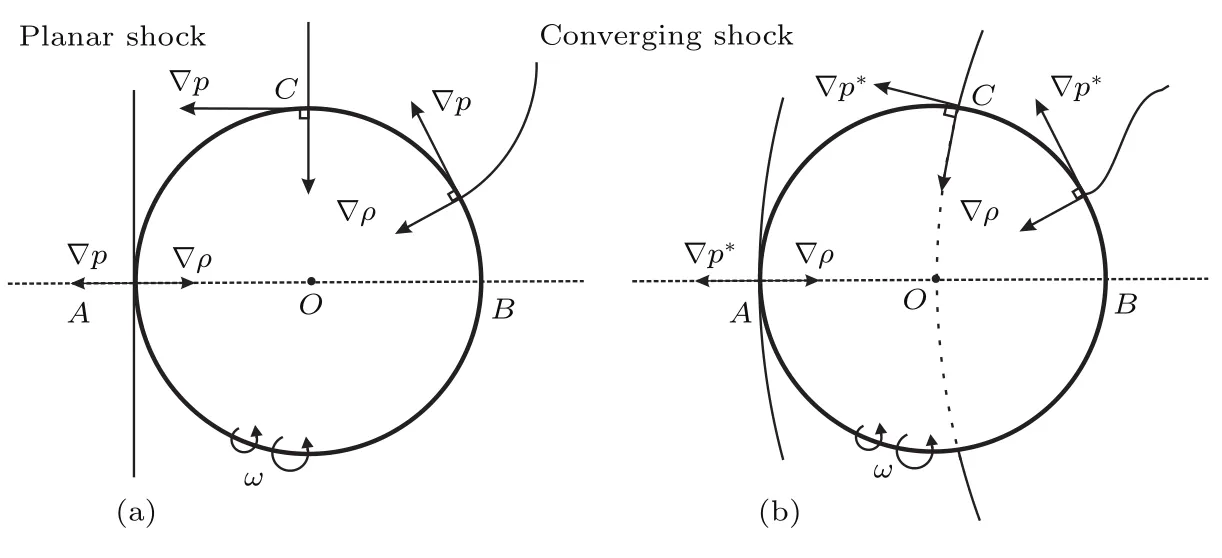
图12 界面上涡量产生示意图 (a)平面激波条件;(b)汇聚激波条件Fig.12. Schem atic sketches of vorticity generation on the interface:(a)P lanar shock cond ition;(b)converging shock cond ition.

在激波离开界面之后,界面上的涡量幅度开始下降.但很快,界面上产生了涡环结构,由于涡结构的自诱导运动,使得涡量逐渐增大,在较长一段时间内,涡环的自诱导运动是涡量增加的主要因素.当反射激波再次作用在界面上时,相比初始入射激波而言,反射激波产生的逆向压力梯度在界面上诱导了负涡量的产生.同时,由于反射激波作用时,界面已经经历了较长时间的演化,界面内外两种气体出现了一定程度的混合,导致密度梯度方向不像入射激波阶段有明显的分布规律.因此,反射激波的作用同样增加了正涡量的产生.

3.6 气泡界面混合程度对比

为了说明汇聚激波和平面激波的冲击对两种气体之间混合程度的影响,本文分别得到了汇聚激波和平面激波与SF6球形气泡相互作用过程中,气泡内SF6与外界空气的混合程度随时间的变化,如图13所示.本文采用了Niederhaus等[7]计算气体混合的方法,其表达式如下:

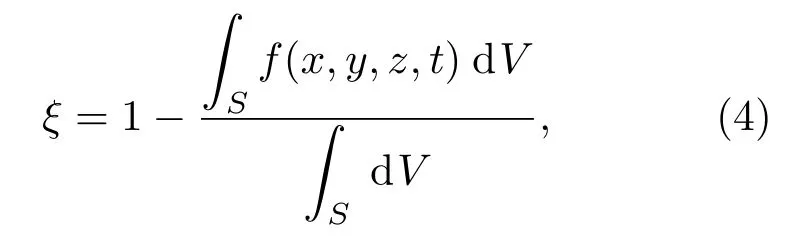
其中,ξ表示界面内外气体的混合程度,反映了在界面计算区域S内环境气体的平均体积分数;f是界面局部微元内SF6所占的体积分数;d V是微元的体积.

在汇聚激波或平面激波与气泡上游界面接触后,气泡内SF6气体与环境空气的混合开始进行,整体呈现了随时间不断增长的趋势.可以发现汇聚激波条件下的混合明显快于平面激波条件,这与汇聚激波运动速度不断增大,在前期相同时间内穿过界面更多面积有关.随后,两个工况下混合程度的增长趋势分别在图13所示的α1点和α2点趋于缓和,对应着二次透射激波以及射流形成的时刻.透射激波在界面内部聚焦后,产生的激波向下游运动并作用于界面,使得界面体积迅速膨胀,导致了环境气体的平均体积分数增长速度减慢,混合速率减小.接下来,两种工况在β1点和β2点处混合速率有明显增高,这对应着气泡外缘的涡环开始形成的时刻,因此涡环的形成促进了气体混合的进行.在涡环得到充分发展以后,平面激波条件下的混合程度趋于稳定.而汇聚激波条件下由于气泡界面上的涡环受到上下壁面的影响,混合程度在一定范围内受到了抑制,表现出不断振动的趋势.

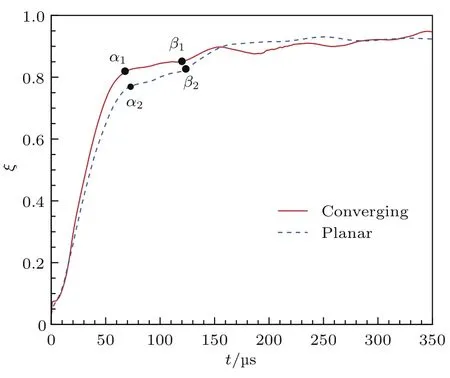
图13 (网刊彩色)激波作用下气泡界面内外气体混合程度Fig.13. (color on line)M ixing between the gases after shock im pact.

4 结 论

本文采用三维程序开展了平面激波以及汇聚激波与球形界面相互作用的数值研究,旨在探讨激波的汇聚效应对流场演化的影响.通过平面激波和汇聚激波作用下气泡界面演化的数值结果与已有的实验结果做比较,验证了数值方法的可靠性.由于激波在汇聚过程中,强度逐渐增大,波后气流速度以及波后压力逐渐升高,壁面效应也逐渐增强.汇聚激波的这些独有特征使得汇聚激波冲击下气泡界面的演化规律相比平面激波条件有较多的不同.首先汇聚激波作用下界面上的涡结构更加尖锐和扁平,这与汇聚激波强度增大导致界面上涡量幅度增大是相关的;其次,由于汇聚激波强度增大,其在界面下游极值点附近形成的最高压力要高于平面激波条件.高压区诱导产生的外向射流结构具有速度快、密度变化快等特点.由于汇聚激波强度的变化以及激波面曲率的存在,对界面上涡量的分布规律以及幅值变化产生了较大的影响.汇聚激波条件下,除了压力梯度和密度梯度夹角不断发生变化外,压力梯度大小同样不断发生变化,这是汇聚激波与平面激波最大的差别.此外,通过对两种工况下界面内外气体混合程度的对比说明汇聚激波更有助于不同气体之间的混合.下一步工作将结合汇聚带来的各种效应进行详细分析.

[1]Ran jan D,Oak ley J,Bonazza R 2011 Annu.Rev.F luid M ech.43 117

[2]Rudinger G,Som ers L M 1960 J.Fluid M ech.7 161

[3]Haas J F,Stu rtevant B 1987 J.Fluid M ech.181 41

[4]Layes G,Jou rdan G,Houas L 2005 Phys.F luids 17 028103

[5]Si T,Zhai Z G,Yang J M,Luo X S 2012 Phys.F luids 24 054101

[6]W ink ler K A,Chalm ers JW,Hodson SW,W oodward P R,Zabusky N J 1987 Phys.Today 40 28

[7]Niederhaus JH,G reenough J A,Oak ley JG,Ranjan D, Anderson M H,Bonazza R 2008 J.F luid M ech.594 85

[8]Zhu Y J,Dong G,Fan B C,Liu Y X 2012 Shock W aves 22 495

[9]Zhai Z G,Si T,Zou L Y,Luo X S 2013 Acta M ech.Sin. 29 24

[10]Sha S,Chen Z H,Zhang Q B 2015 Acta Phys.Sin.64 015201(in Chinese)[沙莎,陈志华,张庆兵2015物理学报64 015201]

[11]Sha S,Chen Z H,Xue D W 2013 Acta Phys.Sin.62 144701(in Chinese)[沙莎,陈志华,薛大文2013物理学报62 144701]

[12]Lind l J D,M cC rory R L,Cam pbell E M 1992 Phys. Today 45 32

[13]Aglitskiy Y,Velikovich A L,Karasik M,M etzler N,Zalesak S T,Schm itt A J,Phillips L,Gardner J H,Serlin V,W eaver J L,Obenschain S P 2010 Philos.T.Roy. Soc.A 368 1739

[14]Bell G I 1951 Los A lam os National Laboratory,Los A lam os,NM,Report LA-1321

[15]P lesset M S 1954 J.Appl.Phys.25 96

[16]Ray leigh L 1883 Proc.London M ath.Soc.14 170

[17]Taylor G 1950 Proc.R.Soc.London A 201 192

[18]Zhai Z G,Liu C L,Qin F H,Yang J M,Luo X S 2010 Phys.F luids 22 041701

[19]W ang X S,Si T,Luo X S,Yang J M 2012 Acta M ech. Sin.44 473(in Chinese)[王显圣,司廷,罗喜胜,杨基明2012力学学报44 473]

[20]Si T,Zhai Z G,Luo X S,Yang J M 2014 Shock Waves 24 3

[21]Si T,Zhai Z G,Luo X S 2014 Laser Part.Beam s 32 343

[22]Yang W H,Luo X S 2014 J.Univ.Sci.Techno l.China 44 488(in Chinese)[杨伟航,罗喜胜2014中国科学技术大学学报44 488]

[23]Zhai Z G,Si T,Luo X S,Yang J M 2011 Phys.F luids 23 084104

PACS:47.20.M aDOI:10.7498/aps.66.064701

N um erical sim u lation o f convergence eff ect on shock-bubb le interactions∗

Liang Yu Guan Ben Zhai Zhi-Gang†Luo Xi-Sheng

(Departm ent ofM odern M echanics,University of Science and Technology of China,Hefei 230027,China)
(Received 7 October 2016;revised m anuscrip t received 25 O ctober 2016)

The shock-bubb le interaction is a basic configuration for studying themore general case of shock-accelerated inhom ogeneous flow s.In p revious studies,a p lanar shock wave interacting w ith a spherical gas bubble was extensively investigated,in which the eff ects of shock intensity,A twood number and secondary shock on the bubble developm ent were considered and elucidated.However,in most of practical app lications,such as inertial confinement fusion,a converging shock wave is generally involved.It is therefore of fundam ental interest to exp lore the perturbation grow th under converging shock conditions.Due to the diffi cu lties encountered in generating a perfectly converging shock wave in laboratory,experimental investigation on the converging shock-accelerated inhomogeneous flows was seldom carried out p reviously.The prelim inary study on the developm ent of a gas bubble im pacted by a converging shock wave showed that a large discrepancy exists com pared w ith the p lanar counterparts.Because of the intrinsic three-dim ensional(3D) features of this prob lem,the current experimental techniques are inadequate to exp lore the detailed diff erences between p lanar and converging shocks accelerating gas bubb les.As a resu lt,num erical simulations becom e im portant and necessary.In thiswork,evolution of an SF6spherical gas bubble surrounded by air accelerated by a cylindrical converging shock wave and a p lanar shock wave is num erically investigated by a 3D program,focusing on the convergence eff ect on the interface evolution.M u lti-com ponent com p ressible Euler equations are adopted in the 3D program and the finite volumemethod is used.The MUSCL-Hancock scheme,a second-order upw ind scheme,is adopted to achieve the second-order accuracy on both tem poral and spatial scales.Com pared w ith p lanar shock wave,a cylindrical converging shock wave has curvature,and as the converging shock wavem oves forward,the shock strength and the wall eff ect both increase,which w ill result in the diversity of the fl ow field after shock im pact.The numerical results show that the vortex rings form ed under converging shock condition are sharper than those under p lanar shock condition which m ay be associated w ith geom etric contraction eff ect of the tube and reflected shock from thewall.Besides,the peak pressure generated in the vicinity of the downstream pole of the bubb le under converging shock condition is higher than that of p lanar shock wave,and,therefore,the jet induced by high pressuresm oves faster under converging shock condition.Due to the variations of shock curvature and shock intensity,the distribution law and am p litude of vorticity generated by converging shock wave at the interface is changed.Com parison between circu lation and gasm ixing rate indicates that the converging shock is beneficial to prom oting vorticity generation and gasm ixing.From the present work,it can be concluded that the convergence eff ect p lays an im portant role in interface evolution.

cylindrical converging shock wave,spherical gas bubble,three-dimensional,numerical simu lation

10.7498/aps.66.064701

∗国家自然科学基金(批准号:11302219)和国家自然科学基金委员会-中国工程物理研究院联合基金(批准号:U 1530103)资助的课题.

†通信作者.E-m ail:san jing@ustc.edu.cn

*Project supported by the National Natural Science Foundation of China(G rant No.11302219)and the Joint Fund of the National Natu ral Science Foundation of China and the China Academ y of Engineering Physics(G rant No.U 1530103).

†Corresponding author.E-m ail:san jing@ustc.edu.cn