弹性需求下的网络交通流逐日动态演化∗

刘诗序陈文思 池其源 严海

1)(福州大学土木工程学院,福州 350116)

2)(北京工业大学北京城市交通协同创新中心,北京 100124)

(2016年12月7日收到;2016年12月28日收到修改稿)

弹性需求下的网络交通流逐日动态演化∗

刘诗序1)†陈文思1)池其源1)严海2)

1)(福州大学土木工程学院,福州 350116)

2)(北京工业大学北京城市交通协同创新中心,北京 100124)

(2016年12月7日收到;2016年12月28日收到修改稿)

在现实交通系统中,网络的交通需求是可变的,随交通运行状态而改变.针对需求可变情形,以含两条路径的简单路网为例,建立了弹性需求下的网络交通流逐日动态演化模型,基于非线性动力学理论,证明了动态演化模型的不动点存在且唯一,并且推导出了弹性需求下网络交通流动态演化的稳定性条件.通过数值实验,分析了网络交通流演化特征.研究发现:在一定条件下流量演化会出现分岔和混沌现象,并且出行者的出行需求对费用越敏感,系统演化越可能稳定;出行者路径选择的随机性越小,系统演化越不可能稳定;出行者对前一天实际费用的依赖程度越小,系统演化越可能稳定.

网络交通流,弹性需求,动态演化,混沌

1 引 言

交通网络平衡分配问题的提出已有几十年的历史,学者们提出了很多扩展的静态模型,如用户平衡分配(user equilibrium,UE)模型[1,2]、随机用户平衡分配(stochastic user equilibrium,SUE)模型[1,2],它是研究网络交通流的主要手段,交通网络平衡分配模型隐含着网络交通流的平衡是可以达到的假设.然而,网络交通流是巨量的出行者路径选择博弈的集聚结果,受到出行者选择行为的影响,现实中出行者的理性程度、出行者获取的信息、出行者个体的差异性等都会影响出行者的路径选择[3].有研究指出,出行者第n天的行为受到第n−1天和之前的行为以及网络状态的影响[1],因此每天的网络交通流不是一成不变的重复,呈现复杂曲折的逐日动态演化过程.研究网络交通流逐日动态演化规律,不仅可以了解交通网络平衡是否能达到以及如何达到的过程,而且还可以认识如果平衡达不到网络交通流演化会出现什么现象.

学者们通过两个途径探索网络交通流逐日动态演化规律.第一个途径以出行者个体选择行为为着眼点,使用计算机微观仿真与行为实验模拟方法,以出行者个体为单元,研究网络交通流的动态演化过程.学者Nakayama等[4]、K lügl和Bazzan[5]、K im等[3]、Wei等[6]、Kusakabe和Nakano[7]、刘天亮和黄海军[8]、刘诗序和关宏志[9]、Iida等[10]、Selten等[11]、Rapoport等[12]做了一些代表性的研究.另一个途径则是从集计角度出发,基于出行者逐日路径选择机理,建立逐日动态分配模型,并以非线性动力学理论为基础,研究网络平衡的存在性及其稳定性,建立的模型分为连续型动态系统(假设出行者出行的天数是连续变量)和离散型动态系统(假设出行者出行的天数是离散变量)两类.学者Sm ith[13,14]、Nagurney和Zhang[15]、Watling[16]、Cho和Hwang[17]、Kumar和Peeta[18]、Tan等[19]、Di等[20]、He和Peeta[21]、Iryo[22]、Xiao等[23]、 郭仁拥和黄海军[24,25]、张波等[26]在连续型动态系统方面做了一些工作.离散型动态系统建模方法最早由Horow itz提出[27],随后,Cantarella和Cascetta[28−30]、Watling和Hazelton[31]、Bie和Lo[32]、He和Liu[33]、Han和Du[34]、Zhao和Orosz[35]、Di和Liu[36]、刘诗序和关宏志等[1,37]、郭仁拥和黄海军等[38−40]、徐红利等[41]学者进一步做了大量的深入研究.最近, Cantarella和Watling[42]将连续模型和离散模型做了统一.

运用非线性动力学方法研究网络交通流逐日动态演化规律,不仅可以推导出网络交通流演化的稳定性条件,而且还可以探索网络交通流不稳定时呈现出的非线性特征.文献[1]对含两条路径的简单路网研究发现了在一定条件下网络交通流量的周期振荡和混沌现象,完善了网络交通流演化研究中不稳定时的规律,文献[37]拓展到有限理性情形.研究表明:网络中出行者理性程度适中时,流量演化容易出现分岔和混沌现象.

然而,上述研究都是针对固定需求的情形,即交通网络的出行需求已知且固定,而在现实中,起讫点(OD)需求可能会受到交通网络运行状态的影响,如当网络中某一对OD之间的拥挤程度增加时,有些出行者可能会改变出行计划(例如放弃自驾选择乘坐地铁出行)或者放弃本次出行,因此出行需求会减小.国内外学者对弹性需求情形下的网络交通流静态分配问题极为关注,提出了很多模型及其求解算法[43−46],但是对弹性需求下网络交通流演化问题还未做深入研究.如果网络的OD需求是可变的,以日为单位,每天的OD需求与交通网络运行状态有关,出行者每天的路径选择受到前一天的行为和网络状态的影响,那么网络交通流的演化是否会稳定？如果不稳定,什么情况出现分岔和混沌？其演化特征和固定需求情形有何不同？

本文以两条路径的简单网络为对象,建立弹性需求下的网络交通流逐日动态演化模型,研究网络交通流动态演化系统平衡点的存在性、唯一性和稳定性,分析弹性需求下网络交通流逐日动态演化规律,探讨系统演化不稳定时出现分岔和出现混沌的条件.

2 模 型

如图1所示,交通网络中OD间有两条平行路径.设第n天的OD需求为d(n),第n天路径1和路径2的流量分别为和,第n天路径1和路径2的实际出行费用为和,假设各路径的出行费用仅与本路径的流量有关,出行费用函数为

图1 路网示意图Fig.1.Road network.

根据随机用户平衡原则的假设[2],出行者获取的信息不完全,设第n天路径r(r=1,2)上的理解出行费用为为可观测部分,为随机误差项.

由假设1可知,第n天路径1和路径2的选择概率为logit型,分别为

式中,θ是与出行者特性有关的参数,且θ＞0,描述出行者路径选择时对路径的费用的敏感程度,θ越大,对路径的费用越敏感,出行者路径选择的随机程度越小,反之,θ越小,对路径的费用越不敏感,出行者路径选择的随机程度越大.根据SUE原则,流量分配为[2,46]

第n天的期望出行费用根据第n−1天期望出行费用和实际出行费用更新,可以表示成二者的加权和[1,44]

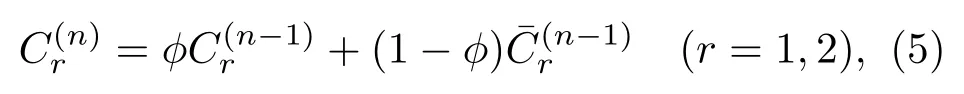
式中,ϕ是与出行者特性有关的参数,且0≤ϕ＜1,其大小反映出行者对前一天实际费用的依赖程度, 0≤ϕ＜1越大,依赖程度越小,反之,ϕ越小,依赖程度越大.

由此得到逐日动态交通流演化模型为

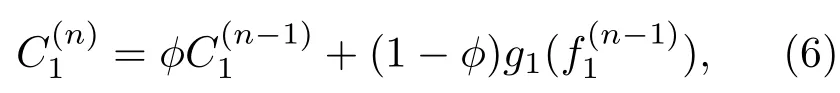
路径流量分配

在弹性需求静态平衡分配问题中,OD需求可表示为期望最小感知成本的单调下降函数[2],因此,第n天的OD需求d(n)可表示为第n天的期望最小感知成本S(n)的单调下降函数,这里设[2,45,46]

式中,d0＞0,表示最大潜在OD需求;β≥0,表示需求量对最小期望感知成本的灵敏度,反映出行者的出行需求对出行费用的敏感性,β越大,出行者的出行需求对费用越敏感,出行者越不愿意出行,反之,β越小,出行者的出行需求对费用越不敏感,出行者出行的愿望越强.

由前面假设出行费用随机误差项服从Gumbel分布,有[2,45,46]

因此

3 稳定性分析和演化状态划分

3.1 不动点的存在性、唯一性和稳定性

设x为一向量,V(x)为一向量值函数,K为一闭凸集.需说明的是,本文所用到的向量均为有限维空间的向量.

定义1 如果[V(x1)−V(x2)]T(x1−x2)≥0,∀x1,x2∈K,则称向量值函数V(x)在K上是单调的[47].

定义2 如果[V(x1)−V(x2)]T(x1−x2)＞0,∀x1,x2∈K,x1̸=x2,则称向量值函数V(x)在K上是严格单调的[47].

引理1 设向量值函数V(x)在K上一阶连续可微,且其Jacobian矩阵∇V(x)是半正定的(正定的),则V(x)是单调的(严格单调的)[47].

假设2 路径的出行费用关于路径流量的函数连续可微,且严格单调增加.

定理1 动态系统(11)和(12)存在唯一的不动点.

由(19)和(20)式,令

向量值函数H(C)在不动点处的Jacobian矩阵

注意到d∗＞0,θ＞0,β≥ 0,p＞0,不难判断出:当β=0时,H(C)的Jacobian矩阵∇H(C)是半正定的,当β＞0时,H(C)的Jacobian矩阵∇H(C)是正定的.根据定义1和定义2得到

由(23)和(24)式知:

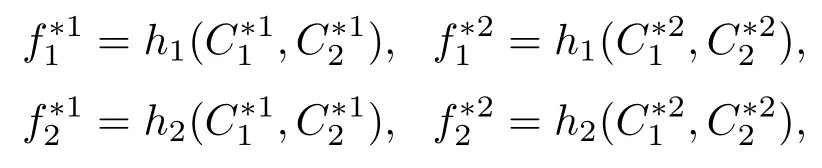
代入(31)式得

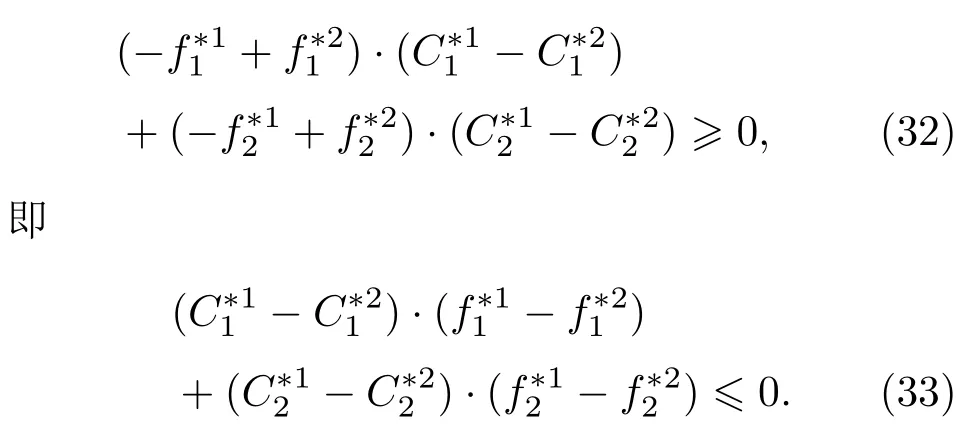
显然,(33)和(28)式矛盾.因此,动态系统(11)和(12)不动点唯一.证毕.

动态系统(11)和(12)的Jacobian矩阵为

在平衡点处

由(25)和(29)式得

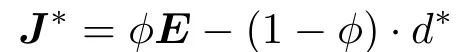
易知:矩阵A有两个正的特征值λ1＞0,λ2＞0,J∗的特征值λJ=ϕ−(1−ϕ)d∗λ1,2.由于0≤ ϕ＜ 1, d∗＞0,所以λJ＜1恒成立,根据非线性动力学稳定性理论[48],当离散型动力系统平衡点Jacobian矩阵的所有特征值的模小于1时平衡点渐近稳定,不难得到定理2.

定理2 弹性需求下两条路径的简单路网逐日动态分配系统平衡点渐近稳定的条件是

不难验证(39)式和文献[1]的稳定性条件一致.判定条件(38)式更具有一般性.

注意到λ1,2,d∗与ϕ无关.因此,不难得到推论1.

推论1 若d∗λ1,2＜1,不论参数ϕ取[0,1)内任何值,弹性需求下两条路径的简单路网交通流逐日动态演化系统平衡点渐近稳定.

推论1表明只要交通系统满足一定条件,不论出行者对信息的依赖程度多大,路网交通流逐日动态演化系统的平衡点渐近稳定.

3.2 演化状态划分

由定理2可知,当(38)式不满足时,网络交通流逐日动态演化出现不稳定情况,根据非线性动力学理论,演化结果将出现周期运动(分岔)或者混沌.

根据混沌理论,当动态系统的Lyapunov指数大于0时,系统才出现混沌.动态系统(11)和(12)有2个Lyapunov指数[48]:

式中,eig(Jn−1Jn−2···J0)表示Jn−1Jn−2···J0的特征值.

由此得到动态系统(11)和(12)的最大Lyapunov指数为

因此,动态系统(11)和(12)演化到稳定的平衡点、周期运动(分岔)和混沌3种状态的条件如表1.

表1 系统逐日动态演化的状态划分Tab le 1.The state of day-to-day dynam ical evolu tion.

通过以上分析可知,弹性需求下网络交通流动态演化系统的平衡点即为弹性需求下的SUE解,但是平衡点在一定条件才稳定(定理2),否则会发生周期运动或混沌运动(表1).下面通过数值实验,来讨论参数θ(表征出行者路径选择时对路径费用的敏感程度)、ϕ(表征出行者对前一天实际费用的依赖程度)、β(表征出行者的出行需求对费用的敏感性)对网络交通流动态演化的影响.注意到θ∈(0,+∞),ϕ∈[0,1),β∈[0,+∞).

4 数值实验

如图1,路网的参数设定同文献[1].路径的行程时间关于流量的函数采用BPR(US Bureau of Public Roads)函数

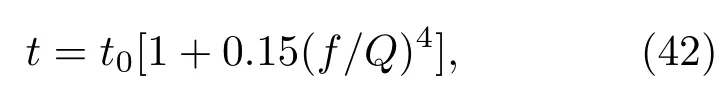
式中t为路径的行程时间,t0为路径的自由流行程时间,f为路径流量,Q为通行能力.设路径1和路径2的自由流行程时间分别为t10=22 m in和t20=25 m in,通行能力分别为Q1=1500辆/h和Q2=2000辆/h;潜在的最大OD需求d0= 1500辆/h;出行费用只考虑出行时间.

4.1 稳定的临界曲线

根据推论1,当θ=0.923时,β=0是稳定临界点,通过不同参数组合的数值实验绘制出系统稳定时β-θ的临界曲线,如图2所示.由图2可知,β的临界值随θ的变化分4个阶段:1)当θ≤0.923时, β的临界值不变(等于0),也即无论β取[0,+∞)的任何值、ϕ取[0,1)的任何值,系统演化都稳定且收敛到平衡点;2)当0.923＜θ≤2.293时,稳定临界点β随θ增大而增大,当θ=2.293时,β达到极大值0.00384;如当θ=1.500时,β=0.0032是稳定临界点,说明,当θ=1.500时,不论β取[0.0032,+∞)的任何值、ϕ取[0,1)的任何值,系统演化都稳定且收敛到平衡点;3)当2.293＜θ≤28.564时,稳定临界点β随θ的增大而减小,当θ=28.564时,β达到极小值0.00154;4)当θ＞28.564时,稳定临界点β随θ的增大而增大.

图2 系统稳定时β-θ的临界曲线Fig.2.The critical curve ofβ-θwhen the system is stab le.

总之,参数β和θ取曲线上方的点时,不论ϕ取[0,1)的任何值,系统演化都稳定且收敛到平衡点,参数β和θ取曲线下方的点时,系统的演化状态与ϕ的取值有关,可能出现分岔或混沌.

4.2 固定β,讨论θ和ϕ不同时系统的演化

情况1 0≤β＜0.00155

以β=0.0002为例,由图2的临界曲线可知,当θ＜0.940时,系统稳定.根据表1的判别条件,经过多次数值实验发现:当θ＞0.940时,系统出现分岔;当θ＞7.295时,系统出现混沌.图3是β=0.0002,θ取不同值时路径1的流量关于参数ϕ的分岔图.

由图2可见,当β=0.0002,θ=0.5时,系统演化是稳定的.由图3(b)和图3(c)可见,当β=0.0002,θ=6或7时,随着ϕ从大到小变化,系统演化出现稳定-倍周期分岔-半周期逆分岔的过程,最后ϕ=0是2周期运动,在文献[1]和其他非线性动力学模型中也可以看到类似的现象[1,49−51].由图3(d)–(h)可见:随着ϕ从大到小变化,系统演化出现稳定-倍周期分岔-混沌-半周期逆分岔的变化过程,最后ϕ=0是2周期运动;从纵轴方向看,在混沌区域中,中间有一些周期3、周期5等奇数周期窗口;从横轴方向看,奇数周期窗口越来越宽,将混沌区域分割成多个带,当θ=8.5时,混沌带可以近似看成1片区域(奇数周期窗口很窄),当θ=16时,周期3窗口变得很宽,混沌区域分成了两个带,当θ=22时,混沌区域分成了3个带,当θ=33时,混沌区域分成了4个带,当θ=40时,混沌区域分成了5个带(最左边的混沌带很窄).

当β=0时,第n天的需求d(n)=d0,弹性需求退化成固定需求情形,文献[1]的研究表明,固定需求下,当θ＜0.923时,系统稳定,当θ＞0.923时,系统出现周期运动,当θ＞6.983时,系统出现混沌现象(更详细的讨论见文献[1]).对比发现, β=0.0002时,随θ的增大,流量演化关于ϕ的分岔图的规律与β=0相似.

根据表1系统逐日动态演化状态划分方法,通过数值实验,绘制出β=0.0002时系统关于参数θ和ϕ的状态划分图,如图4所示.

从图4和图5可以发现,随着β的增大,稳定区域面积越来越大,不稳定区域面积越来越小,特别是混沌区域面积越来越小,这说明β对系统演化的稳定性有“正”作用,从图2的稳定临界曲线也可以看到,当β＞0.00384时,不论参数θ取(0,+∞),ϕ取[0,1)内任何值,系统演化都是稳定的.

图3 (网刊彩色)β=0.0002,θ取不同值时流量关于ϕ变化的分岔图 (a)θ=0.5;(b)θ=6;(c)θ=7; (d)θ=8.5;(e)θ=16;(f)θ=22;(g)θ=34;(h)θ=40Fig.3.(color on line)Flow bifu rcation diagram s w ithϕwhenβ=0.0002 andθis d iff erent:(a)θ=0.5; (b)θ=6;(c)θ=7;(d)θ=8.5;(e)θ=16;(f)θ=22;(g)θ=34;(h)θ=40.

图4 (网刊彩色)β=0.0002时系统关于θ和ϕ的状态划分图Fig.4.(color on line)The system’s state w ithθandϕ whenβ=0.0002.

图5 (网刊彩色)β=0.0007和0.0012时系统关于θ和ϕ的状态划分图 (a)β=0.0007;(b)β=0.0012Fig.5.(color on line)The system’s state w ithθandϕw henβ=0.0007 and 0.0012:(a)β=0.0007;(b)β=0.0012.

图6 (网刊彩色)β=0.00155和0.0018时系统关于θ和ϕ的状态划分图 (a)β=0.00155;(b)β=0.0018Fig.6.(color on line)The system’s state w ithθandϕwhenβ=0.00155 and 0.0018:(a)β=0.00155; (b)β=0.0018.

情况2 0.00155≤β＜0.00233

图6是β=0.00155,0.0018时系统关于参数θ和ϕ的状态划分图.

从图6可见,当β≥0.00155时,不稳定区域分开为两部分,以图6(a)为例,左边部分(θ＜28.352)是周期运动区域,右边部分(θ＞28.352)周期运动和混沌并存.同时,还可以看到,随着β的增大,稳定区域的面积越来越大,不稳定区域面积越来越小.以β=0.00155为例,由图2的临界曲线可知,当θ＜1.096时,系统稳定.根据表1的判别条件,经过多次数值实验发现:当θ＞1.096时,系统出现分岔,当θ＞38.494系统出现混沌.取θ=0.5,8.5, 16,35,38,42,45,50绘制出路径1的流量关于参数ϕ的分岔图,如图7所示.

由图7(b)和图7(c)可以看到,当β=0.00155时,在图6(a)中θ＜28.352的左半不稳定区域,对于固定的θ,流量随ϕ变化的分岔图是相似的,流量演化随ϕ从大到小变化,呈现稳定-2周期分岔过程,也即,系统只有两种状态:稳定状态和2周期运动状态.由图7(d)–(h)可以看到:当β=0.00155时,在θ＞28.352的右半不稳定区域,流量演化关于ϕ的分岔图的规律和β=0.0002的情况类似;当28.352＜θ＜38.494时,流量演化随着ϕ从大到小变化,呈现出现稳定-倍周期分岔-半周期逆分岔的变化过程,最后ϕ=0是2周期运动;当θ＞38.494时,流量演化随着ϕ从大到小变化,呈现出稳定-倍周期分岔-混沌-半周期逆分岔的变化过程,最后ϕ=0是2周期运动.

图7 (网刊彩色)β=0.00155,θ取不同值时流量关于ϕ的变化分岔图 (a)θ=0.5;(b)θ=8.5;(c)θ=16; (d)θ=35;(e)θ=38;(f)θ=42;(g)θ=45;(h)θ=50Fig.7.(color on line)Flow bifu rcation diagram w ithϕw henβ=0.00155 andθis d iff erent:(a)θ=0.5; (b)θ=8.5;(c)θ=16;(d)θ=35;(e)θ=38;(f)θ=42;(g)θ=45;(h)θ=50.

图8 (网刊彩色)β=0.00233,0.0032和0.004时系统关于θ和ϕ的状态划分图 (a)β=0.00233;(b)β=0.0032; (c)β=0.004Fig.8.(color online)The system’s state w ithθandϕwhenβ=0.00233,0.0032,0.004:(a)β=0.00233; (b)β=0.0032;(c)β=0.004.

图9 β=0.00233,θ=3时流量关于ϕ的变化分岔图Fig.9.(color on line)Flow bifu rcation d iagram w ithϕ whenβ=0.00233 andθ=3.

情况3 β≥0.00233

图8是β=0.00233,0.0032,0.004时系统关于参数θ和ϕ的状态划分图.图9是β=0.00233, θ=3时,流量关于ϕ的变化分岔图.

对比图6(a)和图6(b)以及图8(a)和图8(b),可以发现,当β≥0.00233时,系统不稳定的右半部分区域消失,此时混沌现象也消失,从图9还可以看到,系统不稳定的状态是2周期运动.从图8(a)–(c)可以看到,随着β的增大,周期运动区域面积逐渐减小,最后完全是稳定状态,通过多次数值实验得到,当β≥0.00384时,系统完全是稳定状态,也即,当β≥0.00384时,不论θ取(0,+∞)内任何值、ϕ取[0,1)内任何值,系统演化都稳定,这一结论也可以从图2的系统稳定时β-θ的临界曲线得出.

4.3 固定θ,讨论β和ϕ不同时系统的演化

图10是θ=0.5,3,9,25时系统关于参数β和ϕ的状态划分图.

从图10可见,当θ较小时,系统都是稳定的,随着θ的增大,先出现周期运动,后出现混沌现象.经过多次数值实验发现:当θ≤0.923时,系统演化稳定,即当θ≤0.923时,无论β取[0,+∞)的任何值、ϕ取[0,1)的任何值,系统演化都稳定且收敛到平衡点;当0.923＜θ≤6.983时,系统出现周期运动;当θ＞6.983时,系统出现混沌.注意到,系统出现分岔和混沌的θ的临界值和β=0时是一致的[1].

图10 (网刊彩色)θ取不同值时系统关于β和ϕ的状态划分图 (a)θ=0.5;(b)θ=3;(c)θ=9;(d)θ=25Fig.10.(color on line)The system’s state w ithβandϕwhenθis d iff erent:(a)θ=0.5;(b)θ=3;(c)θ=9; (d)θ=25.

4.4 固定ϕ,讨论β和θ不同时系统的演化

图11是ϕ=0,0.05,0.3,0.8,0.86,0.9时系统关于参数β和θ的状态划分图.

从图11可以看出,当ϕ较小时,系统演化稳定或者周期运动;当ϕ比较大时,系统演化稳定;当ϕ取中间值时,系统演化有稳定、周期运动和混沌状态.经过多次数值实验发现:当ϕ≤0.036时,系统是稳定的或周期运动的;当0.036＜ ϕ＜ 0.85时,系统是稳定、周期运动或者混沌状态;当0.85≤ ϕ＜ 0.89时,系统演化是稳定的或周期运动的;当0.89≤ϕ＜1时,系统演化是稳定的.同时,从图11还可以发现,随着ϕ的增大,稳定区域的面积越来越大,不稳定区域的面积越来越小,直到ϕ=0.89时整个区域都是稳定的.

4.5 系统演化规律

根据以上的分析可知,参数θ(表征出行者路径选择时对路径的费用敏感程度),ϕ(表征出行者对前一天实际费用的依赖程度),β(表征出行者的出行需求对费用的敏感程度)对网络交通流的逐日动态演化都有影响.

1)临界曲线特征

若对任意的ϕ∈[0,1)动态系统演化都稳定,那么临界曲线β随θ的变化为:当θ≤0.923时,β的临界值不变(等于0);当θ＞0.923时,β先增大后减小,然后又增大,β出现极大值点0.00384(当θ=2.293时)和极小值点0.00154(当θ=28.564时).

2)参数β对系统演化的影响

①当0≤β＜0.00155时,对于固定的β,随θ的增大,系统演化关于ϕ的分岔图的规律与β=0相似.即θ较小时,系统稳定;θ取中间值时,系统随着ϕ从大到小变化出现稳定-倍周期分岔-半周期逆分岔的过程,最后ϕ=0是2周期运动;θ较大时,系统随着ϕ从大到小变化出现稳定-倍周期分岔-混沌-半周期逆分岔的变化过程,最后ϕ=0是2周期运动.

②当0.00155≤β＜0.00233时,对于固定的β,系统关于参数θ和ϕ的状态的划分图的不稳定区域分开为左右两部分:左边是2周期运动区域,右边周期运动和混沌并存.

图11 (网刊彩色)ϕ取不同值时系统关于β和θ的状态划分图 (a)ϕ=0;(b)ϕ=0.05;(c)ϕ=0.3;(d)ϕ=0.8; (e)ϕ=0.86;(f)ϕ=0.9Fig.11.(color on line)The system’s state w ithβandθwhenϕis d iff erent:(a)ϕ=0;(b)ϕ=0.05; (c)ϕ=0.3;(d)ϕ=0.8;(e)ϕ=0.86;(f)ϕ=0.9

③当0.00233≤β＜0.00384时,对于固定的β,系统关于参数θ和ϕ的状态的划分图的不稳定区域只有一个区域,并且不稳定状态是2周期运动状态.

④当β≥0.00384时,系统完全是稳定状态(与参数θ和ϕ无关).

⑤随着β的增大,系统关于参数θ和ϕ的状态的划分图的稳定区域面积越来越大,最后当β≥0.00384时,系统完全是稳定状态.

3)参数θ对系统演化的影响

当θ≤0.923时,系统演化稳定(与参数β和ϕ无关);当0.923＜θ≤6.983时,系统出现周期运动;当θ＞6.983时,系统出现混沌.

4)参数ϕ对系统演化的影响

①当0.89≤ϕ＜1时,系统演化是稳定的;当ϕ≤0.036或0.85≤ϕ＜0.89时,系统是稳定的或周期运动的,当0.036＜ϕ＜0.85时,系统是稳定、周期运动或者混沌状态.

②随着ϕ的增大,系统关于参数β和θ的状态划分图的稳定区域的面积越来越大,直到ϕ=0.89时整个区域都是稳定的.

5 结 论

本文假设交通需求是弹性的,以两条平行路径的简单路网为例,建立了逐日动态交通流演化模型(固定需求是β=0时的特殊情形),在数值实验中,通过改变与出行者特性有关的参数β,θ和ϕ的取值,分析系统的演化规律.研究结论如下.

1)弹性需求动态系统的不动点存在且唯一(定理1),平衡点渐近稳定需要满足一定的条件(定理2).

2)若对任意的ϕ∈[0,1)动态系统演化都稳定,那么临界曲线β随θ的变化为:当θ≤0.923时,β的临界值等于0;当θ＞0.923时,β先增大后减小,然后又增大.

3)系统演化随参数β,θ和ϕ的变化呈现复杂的特征,有稳定、分岔和混沌现象.总体上,参数β对系统的稳定性有“正”作用,即出行者的出行需求对费用越敏感,系统演化反而越可能稳定,当β≥0.00384时,系统完全是稳定状态;参数θ对系统的稳定性有“负”作用,即出行者路径选择时对路径的费用越敏感,系统演化越不可能稳定,换言之,出行者路径选择的随机性越小,系统演化越不可能稳定;参数ϕ对系统的稳定性有“正”作用,即出行者对前一天实际费用的依赖程度越小,系统演化越可能稳定.

注意到参数β反映的是出行者的出行意愿(是否出行),β越大,出行者的出行需求对费用越敏感,出行者越不愿意出行,总的出行者数量就越小,系统越有可能稳定.参数θ反映的是出行者一旦出行了,他在选择路径时路径的费用的影响程度(如何出行),θ越大,出行者路径选择时对路径的费用越敏感,出行者路径选择的随机性越小,出行者越倾向于选择最短路径,而不是分散地选择所有路径,系统越不可能稳定.因此,微观个体出行者在做是否出行和如何选择路径决策时,路径的费用的敏感性对网络交通流演化的影响效果不同.

需要说明的是,本文的结论只在两条路径的简单网络中才成立,对于现实中的复杂网络,可以参考本文的研究方法,分析网络交通流逐日动态演化规律.对于更复杂的交通网络,其网络交通流动态演化模型是高维的非线性动力学模型,但是分岔和混沌现象也应该存在,只不过这时的非线性现象可能更加复杂,如可能会出现多个分岔和混沌的临界点,甚至在一定条件下还可能出现超混沌现象.

[1]Liu S X,Guan H Z,Yan H 2012 Acta Phys.Sin.61 090506(in Chinese)[刘诗序,关宏志,严海2012物理学报61 090506]

[2]Sheffi Y 1985 Urban Transportation Networks:Equilibrium Ana lysisw ith M athem atica l Programm ing M ethods (Englewood C liff s:Prentice-Hall,Inc.)pp59–61,309

[3]K im H,Oh J S,Jayak rishnan R 2009 KSCE J.Civil Engineer.13 117

[4]Nakayam a S,K itam ura R,Fu jii S 1999 Transp.Res. Rec.1676 30

[5]K lügl F,Bazzan A L C 2004 J.Artifi cial Societies and Social Sim u lation 7 1

[6]W ei F F,M a S F,Jia N 2014 M ath.Probl.Eng.204 1

[7]K usakabe T,Nakano Y 2015 Transp.Res.C 59 278

[8]Liu T L,Huang H J 2007 Acta Phys.Sin.56 6321(in Chinese)[刘天亮,黄海军2007物理学报56 6321]

[9]Liu S X,Guan H Z 2013 China Civil Eng.J.46 136(in Chinese)[刘诗序,关宏志2013土木工程学报46 136]

[10]Iida Y,Akiyam a T,Uchida T 1992 Transp.Res.B 26 17

[11]Selten R,Chm u ra T,Pitz T,K ubec S,Sch reckenberg M 2007 Gam e Econ.Behav.58 394

[12]Rapoport A,G isches E J,Daniel T 2014 Transp.Res. B 68 154

[13]Sm ith M J 1984 Transp.Sci.18 245

[14]Sm ith M J,Watling D P 2016 Transp.Res.B 85 132

[15]Nagu rney A,Zhang D 1997 Transp.Sci.31 147

[16]W atling D 1999 Transp.Res.B 33 281

[17]Cho H J,Hwang M C 2005 M ath.Com put.M odel.41 501

[18]Kum ar A,Peeta S 2015 Transp.Res.B 80 235

[19]Tan Z,Yang H,Guo R Y 2015 Transp.Res.C 61 87

[20]D i X,Liu H X,Ban X X,Yu J W 2015 Netw.Spat. Econ.15 537

[21]He X Z,Peeta S 2016 Transp.Res.B 84 237

[22]Iryo T 2016 Transp.Res.B 92 88

[23]X iao F,Yang H,Ye H B 2016 Transp.Res.B 86 86

[24]Guo R Y,Huang H J 2008 J.M anag.Sci.in China 11 12(in Chinese)[郭仁拥,黄海军 2008管理科学学报 11 12]

[25]Guo R Y,Yang H,Huang H J,Tan Z J 2015 Transp. Res.B 71 248

[26]Zhang B,Juan Z C,N i A N 2014 J.Ind.Eng.Eng. M anag.28 164

[27]Horow itz J L 1984 Transp.Res.B 18 13

[28]Cascetta E,Cantarella G E 1991 Transp.Res.A 25 277

[29]Cantarella G E,Cascetta E 1995 Transp.Sci.29 305

[30]Cantarella G E 2013 Transp.Res.C 29 117

[31]W atling D,Hazelton M L 2003 Netw.Spat.Econ.3 349

[32]Bie J,Lo H K 2010 Transp.Res.B 44 90

[33]He X,Liu H X 2012 Transp.Res.B 46 50

[34]Han L,Du L 2012 Transp.Res.B 46 72

[35]Zhao X,O rosz G 2014 Physica D 275 54

[36]Di X,Liu H X 2016 Transp.Res.B 85 142

[37]Li T,Guan H Z,Liang K K 2016 Acta Phys.Sin.65 150502(in Chinese)[李涛,关宏志,梁科科2016物理学报65 150502]

[38]Guo R Y,Yang H,Huang H J 2013 Transp.Res.C 34 121

[39]Guo R Y,Huang H J 2016 Transp.Res.C 71 122

[40]YangW J,Guo R Y,LiQ 2015 Syst.Eng.Theory Pract. 35 3192(in Chinese)[杨文娟,郭仁拥,李琦2015系统工程理论与实践35 3192]

[41]Xu H L,Yu X L,Zhou J 2015 J.M anag.Sci.China 18 39(in Chinese)[徐红利,于新莲,周晶2015管理科学学报18 39]

[42]Cantarella G E,W atling D P 2016 Euro.J.Transp.Logist.5 69

[43]Daferm os S 1982 Networks 12 57

[44]Cantarella G E 1997 Transp.Sci.31 107

[45]Yu Q,Fang D B,Du W 2014 Eur.J.Oper.Res.239 112

[46]Zhou J 2001 J.Syst.Engineer.16 88(in Chinese)[周晶2001系统工程学报16 88]

[47]Nagu rney A 1999 Network Econom ics:A Variational Inequality Approach(Boston:K luwer Academ ic Publishers)pp17–19

[48]Liu Z H 2006 Fundam en tals and Applications ofChao tic Dynam ic(Beijing:Higher Education Press)pp24–29, 60–61(in Chinese)[刘宗华 2006混沌动力学基础及其应用(北京:高等教育出版社)第24—29,60—61页]

[49]Stone L 1993 Nature 365 617

[50]Yu W B,W ei X P 2006 Acta Phys.Sin.55 3969(in Chinese)[于万波,魏小鹏2006物理学报55 3969]

[51]Peng M S 2005 Chaos Solitons Fract.25 1123

PACS:05.45.–a,05.45.Gg,05.45.Pq,01.75.+mDOI:10.7498/aps.66.060501

Day-to-day dynam ical evo lu tion of netw ork traffi c fl ow w ith elastic dem and∗

Liu Shi-Xu1)†Chen Wen-Si1)ChiQi-Yuan1)Yan Hai2)

1)(School of Civil Engineering,Fuzhou University,Fuzhou 350116,China)
2)(Beijing Collaborative Innovation Center for M etropolitan Transportation,Beijing University of Technology, Beijing 100124,China)
(Received 7 Decem ber 2016;revised m anuscrip t received 28 Decem ber 2016)

Network traffi c fl ow is an aggregated result of a huge number of travelers’route choices,which is in fluenced by the travelers’choice behaviors.So day-to-day traffi c fl ow is not static,but presents a com p lex and tortuous day-to-day dynam ic evolution p rocess.Studying day-to-day dynam ic evolution ofnetwork traffi c flow,we can not only know whether the traffi c network equilibrium can be reached and how the p rocess is achieved,but also can know what phenomenon w ill occur in the evolution of network traffi c flow if the equilibrium is not reached.In a real traffi c system,taking day as scale unit,the day-to-day network traffi c dem and is variable and changes w ith everyday’s traffi c network state.The travelers’route choices are also influenced by the previous day’s behaviors and network state.Then,w ill the day-to-day network traffi c flow evolution be stable?If it is unstable,when w ill bifurcation and chaos occur?In this paper we discuss the day-to-day dynam ic evolution of network traffi c fl ow w ith elastic dem and in a sim p le two-route network. The dynam ic evolution model of network traffi c fl ow w ith elastic demand is formulated.Based on a non linear dynam ic theory,the existence and uniqueness of the fixed point of dynam ic evolution m odel are proved,and an equilibrium stability condition for the dynam ic evolution of network traffi c flow w ith elastic demand is derived.Then,the evolution of network traffi c flow is investigated through num erical experim ents by changing the three param eters associated w ith travelers,which are the sensitivity of travelers’travel dem and to travel cost,the random ness of travelers’route choices, and travelers’reliance on the previous day’s actual cost.Our findings are as follows.Firstly,there are three kinds of final states in the evolution of network traffi c flow:stability and convergence to equilibrium,periodicm otion and chaos. The final state of the network traffi c flow evolution is related to the above three param eters.It is found that under certain conditions the bifurcation diagram of the network traffi c flow evolution reveals a com p licated phenomenon of period doubling bifurcation to chaos,and then period-halving bifurcation.M eanwhile,the chaotic region is interspersed w ith odd periodic w indows.M oreover,them ore sensitive to cost the travelers’travel dem and them ore likely the system evolution is to be stable.The smaller the randomness of travelers’route choices,the less likely the system evolution is to be stable.The lower the degree of travelers’reliance on the previous day’s actual cost,the m ore likely the system evolution is to be stable.

network traffi c flow,elastic demand,dynam ical evolution,chaos

10.7498/aps.66.060501

∗国家自然科学基金(批准号:51308126,51378036,51308018)资助的课题.

†通信作者.E-m ail:liushixu@fzu.edu.cn

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.51308126,51378036,51308018).

†Corresponding author.E-m ail:liushixu@fzu.edu.cn