径向开槽薄圆环振子径向振动分析*
2017-08-02刘世清李陆化
李 丹, 刘世清, 李陆化
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
径向开槽薄圆环振子径向振动分析*
李 丹, 刘世清, 李陆化
(浙江师范大学 数理与信息工程学院,浙江 金华 321004)
为研究径向开槽圆环的径向振动特性,基于机电类比原理,建立了开槽圆环的径向振动等效电路,并得出其共振频率方程,探讨了圆环第1、第2阶共振频率及振幅放大系数与其半径比的关系.结果表明:圆环第1阶共振时振幅放大系数随半径比的增大而增大,第2阶共振时振幅放大系数随半径比的增大而下降;其共振频率随半径比的增大而单调上升;理论与有限元数值仿真结果基本一致.
圆环振子;径向振动;共振频率;位移放大系数;有限元分析
0 引 言
在功率超声领域,除了需要设计各种结构和振动模式的振动系统外,还需要通过对弹性振动体结构进行特殊的设计,如开狭槽或狭缝等,来产生一些特殊模式的振动,以满足不同的应用需要.如纵扭复合振动等[1].文献[2]通过开槽的方法提出一种可显著提高超声焊接质量的纵扭振动传振杆,该系统还可用作超声波电机定子驱动器.在超声焊接等大功率应用领域,常采取在大尺寸变幅杆(工具头)上开设一系列平行狭缝的方式来减弱其纵横耦合振动,提高工具头的位移振幅,以提高系统的纵向声能传输效率[3].
近年来在超声拉拔金属成型领域,为提高超声拉拔效率及改善拉拔质量,一类径向振动盘形超声聚能器发展起来了[4-6]. 文献[7]利用解析法研究锥形等几种圆盘聚能器的径向和扭转振动特性,并得出了共振频率方程;文献[8]与文献[9]分别对等厚度及变厚度圆环振子的径向及扭转振动特性进行了研究,得到了系统的机电等效电路及频率方程.
为进一步改善此类环形超声聚能器的振动性能,本文提出径向开槽薄圆盘聚能器振子.径向开槽的目的:一方面可降低圆环振子的共振频率;另一方面可将圆盘的径向振动尽可能转换为槽与槽间隔部分的纵振动,以利于提高振动能量的传输效率.本文依据弹性力学理论及机电类比原理,建立了其径向振动机电等效电路,导出了其工作频率方程,并进行了有限元数值仿真分析.
1 径向开槽圆环振子的径向振动分析
图1所示为一个沿半径方向开有一系列狭槽的薄环形弹性振子,其内、外半径分别为b,c,厚度为h.Fb,Fc分别表示振子内、外辐射面处的外力,vb,vc分别表示振子内、外辐射面处的质点振动速度.在柱坐标系中,振子径向振动的运动方程为[9]
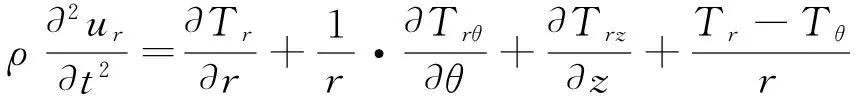
(1)
式(1)中:ur表示径向位移分量;Tr,Tθ,Trθ,Trz分别表示振子内部各应力的分量.在极坐标系中,应变和位移的关系为
(2)
式(2)中:Sr表示振子应变分量.由广义胡克定律知,应力与应变的关系为
(3)
式(3)中:G=E/[2(1+υ)]为材料剪切模量;E,υ分别为材料弹性模量和泊松系数.振子实际作复杂的三维耦合振动.为简化分析,作如下假设:
1)振子厚度h远小于其直径,即为薄圆环.
2)狭槽数量足够多,其长度与振子环宽相当.由于狭缝的分割,可近似地认为环中切应力为零.
3)不计狭槽对振子等效质量的影响,振子作轴对称平面径向振动.
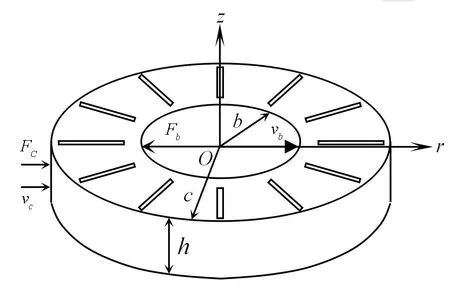
图1 径向开槽弹性薄圆环振子示意图
依据上述假设,正应力Tr是振子中唯一不等于零的量,其余各应力分量及υ均近似为零.由上述各方程化简得振子的径向振动波动方程为
(4)
(5)
由式(5)可得振子的径向振速表达式
环形振子中的径向正应力为
(7)
式(7)中:k=ω/υr,ω为角频率;J0(kr),J1(kr)和Y0(kr),Y1(kr)分别为第一类和第二类零阶、一阶贝塞尔函数;C1,C2为待定常数,由振子径向边界条件确定.
2 圆环振子振幅放大系数
令圆环外表面处质点振幅为uc,圆环作自由径向振动时的边界条件为
(8)
由式(5)和式(7)可得:
(9)
C1J1(kb)+C2Y1(kb)=0.
(10)
由式(9)和式(10)得圆环径向位移分布函数为
(11)
这里,定义圆环振幅放大系数M为内外表面质点振幅之比,即
(12)
3 圆环振子径向振动等效电路
(13)
(14)
(15)

(16)
式(15)和式(16)中:Sb=2πbh,Sc=2πch分别为振子内、外侧面积.由四端网络理论,并结合贝塞尔函数的递推关系
式(15)和式(16)可进一步化为:
(17)
Fb=z3υc+(z2+z3)υb.
(18)
式(17)和式(18)中
(19)
(20)
(21)
式(19)和式(20)中:zb=ρυrSb;zc=ρυrSc.
综上,由等效电路理论可得径向开槽圆环振子径向振动的机电等效电路如图2所示.
由图2可得开槽圆环自由振动的频率方程

(22)
将z1,z2,z3的表达式代入式(22),得振子共振频率方程的具体表达式为
(23)
利用频率方程式(23)可得径向开槽圆环振子的共振频率随几何尺寸的变化关系.
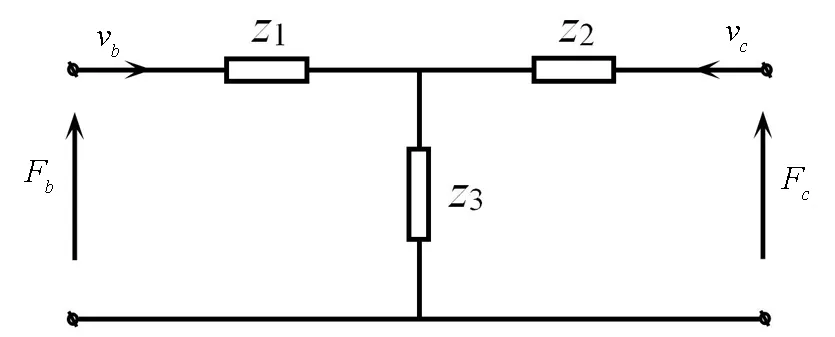
图2 径向开槽弹性薄圆环振子等效电路
作为算例,笔者计算了材料为铝的径向开槽圆环振子共振频率f及振幅放大系数M随内外半径比γ的变化关系分别如图3和图4所示.这里满足γ=b/c.计算中,圆环外径c=64 mm,厚度h=7 mm,且保持不变,通过改变圆环内径b来改变其内外半径比.
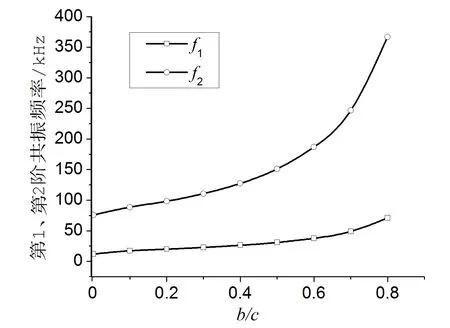
图3 振子第1、第2阶共振频率与半径比关系
由图3可得,径向开槽圆环振子的第1、第2阶共振频率随半径比增大均单调上升,这与无槽圆环振子的径向振动特性不同[9].
由图4可以看出,振子的第1阶共振位移振幅放大系数随半径比增大(环宽变小)而增大,但不显著;其第2阶共振位移振幅放大系数随半径比的增大而单调降低,且在半径比较小时,远大于第1阶振幅放大系数.
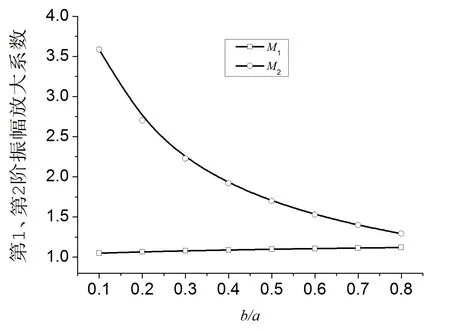
图4 振子第1、第2阶共振位移放大系数与半径比关系
4 有限元仿真
采用ANSYS有限元软件对振子的径向振动模态进行了仿真分析.圆环振子材料为铝,其材料参数分别为:密度ρ=2 700 kg/m3;泊松系数υ=0.34;几何参数分别为:外径c=64 mm,内径b=30 mm,厚度h=7 mm,狭槽长度均为12.5 mm.

表1 圆环振子共振基频理论与仿真值
由表1可以看出,当所开狭槽数较少时,理论与仿真结果偏差较大,但随着圆环中槽数的增加,相对误差逐渐减小.这是因为理论是基于狭槽数量足够多的假设而推导得到时.图5和图6分别是狭槽数为18的圆环振子的基频共振模态振型及相应的位移向量分布图.
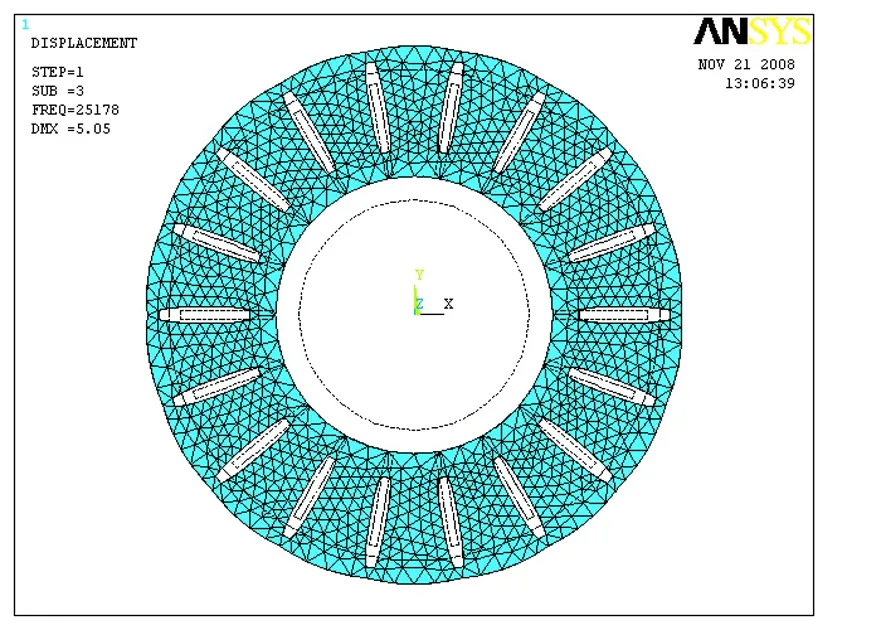
图5 圆环振子基频共振模态 图6 圆环振子中基频共振位移向量分布
5 结 论
本文对径向开槽薄圆环振子的径向振动特性进行了研究,得出了其机电等效电路及共振频率方程.通过数值计算探讨了振子的共振频率与位移放大系数随其几何尺寸的变化关系.研究表明,径向开槽圆环振子的第1、第2阶共振频率均随其内外半径比的增大而单调升高;振子第1阶共振位移放大系数随内外半径比的增大而增大,而第2阶共振时却随之单调降低,且在半径比较小,即环宽较大时,第2阶共振位移放大系数远大于第1阶.从工程应用上讲,采用第2阶共振模式工作优于第1阶.
[1]Lin S E.Study on the longitudinal-torsional composite mode exponential ultrasonic horns[J].Ultrasonics,1996,34(7):757-762.
[2] Tsujino J,Ueoka T,Otoda K,et al.One-dimensional longitudinal-torsional vibration converter with multiple diagonally slitted parts[J].Ultrasonics,2000,38(8):72-76.
[3]林仲茂.超声变幅杆的原理与设计[M].北京:科学出版社,1987.
[4]Siddiq A,Sayed T E.Ultrasonic-assisted manufacturing prosesses:Variational model and numerical simulation[J].Ultrasonics,2012,52(4):521-529.
[5]Siegert K,Uner J.Superimposing ultrasonic waves on the dies in tube and wire drawing[J].Journal of Engineering Material and Technology,2001,123(4):517-523.
[6]谢涛,齐海群,张俊.超声振动拉丝实验研究[J].中国机械工程,2006,17(3):224-226.
[7]汪承灏.盘形聚能器的设计理论[J].声学学报,1979(4):279-287.
[8]苏超,刘世清,王家涛.幂函数剖面薄圆环振子的扭转振动特性[J].浙江师范大学学报:自然科学版,2012,35(3):284-289.
[9]林书玉.弹性薄圆环的超声频径向振动及其等效电路研究[J].声学学报,2003,28(2):102-106.
(责任编辑 杜利民)
A study on the radial vibration of a circular ring with radial slots
LI Dan, LIU Shiqing, LI Luhua
(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)
The radial vibration of a circular ring with multiple radial slots was studied. Based on the electro-mechanical analogy, the equivalent circuit and the frequency equation of the slitted circular ring in radial vibration were derived. By numerical calculation, the relationship between the displacement amplitude magnification factor as well as the resonance frequency of the ring in the first and second order vibration and its radius ratio were investigated. It was showed that the amplitude magnification factor of the ring increased in the first resonance while decreased in the second resonance with the increase of its radius ratio, and the resonance frequency increased with the radius ratio increased. The theoretical resonance frequencies were in good agreement with that of the FEM simulations.
circular ring vibrator; radial vibration; resonance frequency; the amplitude magnification factor; FEM simulation
10.16218/j.issn.1001-5051.2017.01.005
2016-05-11;
2016-06-20
国家自然科学基金资助项目(11274279;11074222)
李 丹(1992-),女,安徽蚌埠人,硕士研究生.研究方向:功率超声.
刘世清.E-mail: zjnulsq@163.com
O426
A
1001-5051(2017)01-0031-05
