微积分思想在保险精算课程教学中的应用

姚俊

(常州工学院教学质量评估中心，江苏常州213032)

微积分思想在保险精算课程教学中的应用

姚俊

(常州工学院教学质量评估中心，江苏常州213032)

在数学与应用数学专业的课程体系中设置保险精算课程，既有助于精算教育的推广，也符合学生多样化发展的需求。为提高课程目标达成度，将微积分思想融入保险精算的教学过程，从导数定义的角度阐述了利息强度和死力两个概念的本质内涵，用微元法重新推导了连续条件下人寿保险的一些精算公式。

保险精算；导数；微元法；精算现值

0 引言

保险精算学是依据经济学的基本原理和知识，利用现代数学方法，对各种保险经济活动未来的财务风险进行分析、估价和管理的一门综合性应用科学。例如研究保险事故的出险规律、保险事故损失额的分布规律、保险人承担风险的平均损失及其分布规律、保险费率和责任准备金、保险公司偿付能力等保险具体问题。

自从1988年北美精算协会与南开大学联合招收了我国第一批精算学硕士研究生以来，我国精算教育呈现多元化趋势，不仅知名高等学府纷纷加入了精算教育队伍，许多地方本科院校也根据社会发展和人才培养的需要尝试将保险精算课程纳入统计学、数学与应用数学等专业的课程体系之中。我国高等教育学会副会长张德祥教授认为：专业就其本质来说，是围绕人才培养目标形成的课程组合。一个专业总有一定的培养目标，围绕这个培养目标设计一系列的课程，这样专业就形成了[1]。因此，课程的适切性问题始终是高等学校在设计课程时绕不开的话题，在数学与应用数学等非精算专业或方向开设保险精算课程亦是如此。国内精算教育工作者对保险精算课程内容的适切性[2-3]、课程组织的适切性[4-5]、课程结构的适切性[6-7]以及课程选择的适切性[8]等方面进行了许多有益的探索和思考，但是大多围绕保险精算课程教学的宏观层面，而对教学过程的微观层面探讨甚少，例如课堂教学中如何体现专业背景和主专业知识结构对保险精算知识模块的支撑。因此，文章基于数学与应用数学专业的优势背景，将微积分思想引入保险精算课程的课堂教学之中，以供精算教育工作者在实践中参考。

1 微分思想在保险精算教学中的应用

用导数数学方法研究非均匀变化的变量的变化率问题是“以匀代变，无限逼近”微积分思想的一个体现。保险精算理论借助导数符号分别定义了利息强度和死力这两个概念，但是一般教材上都以函数相对变化率的形式直接给出，初学者会觉得很突兀。而利息强度、死力是保险精算基础中的重要概念，后期的精算数理中很多精算公式都要用到这两个量来表达，因此在教学过程中有必要从导数定义的角度剖析这两个概念的本质内涵及其作用。

1.1 利息强度的微分解释

在利息理论中，利息强度(或利息力)是指某一时点处利息大小的度量。任意时点t处的利息强度被定义为

(1)

式中a(t)为积累函数[9]10。

上述推导过程表明：利息强度在数学上是“Δt时间内平均利息的极限”，即一单位本金在t时的变化率，其大小反映了一单位本金在瞬间产生利息的能力。

进一步，还可以利用导数的定义得到每年计息m次的年名义利率i(m)、年名义贴现率d(m)与利息强度之间的关系(见文献[10])。特别地，若某时间区间上利息强度δt恒为常数δ，则有

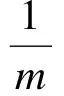
而

从而有

(2)

又因为

所以

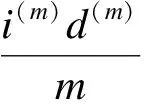
代入(2)式，得

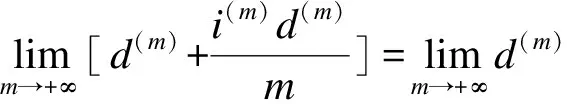
(3)

式(2)、(3)表明，时间区间上恒为常数的利息强度就是每年计息“无穷多次”的年名义利率或年名义贴现率。

1.2 死力的微分解释

在生命表基础中，新生婴儿在任意年龄x处的死力(或死亡力)被定义为

(4)

式中，s(x)为生存函数[9]36。

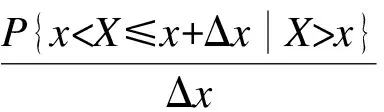
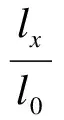
(5)

式(5)表明，死力在数学上是存活人数在x岁时的变化率。

2 积分思想在保险精算教学中的应用

用定积分数学方法研究非均匀变化的变量的累积问题是“以匀代变，无限逼近”微积分思想的另一个体现。而定积分解决实际问题的关键是微元法(元素法)确定积分表达式，该方法包含了另一个微积分思想“非线性函数局部线性化”。在研究人寿保险的趸缴纯保费、责任准备金等精算问题时，教材一般都采用“余命随机变量函数的数学期望”这一思路。但是注意到离散条件下人寿保险的各种精算公式都是求和的形式，这说明趸缴纯保费、责任准备金等本质上是累积问题，因此我们有理由用微元法来推导连续条件下人寿保险的各种精算公式。

2.1 微元法计算连续年金的现值和终值

连续付款n个计息期，每个计息期付款额之和为1的连续年金的现值为

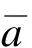
(6)

式中，ν为折现因子[9]29。

式(6)可由微元法推导而得。连续年金的现值与付款时间t有关，且t∈[0,n]，从中任取一子区间[t,t+dt]。因为每个计息期付款总额为1，所以dt时间内付款dt=Δt单位。若时刻t支付这Δt单位，在时刻0的现值为νt·Δt；若时刻t+dt支付，在时刻0的现值为νt+Δt·Δt。这样，连续年金在[t,t+dt]上的现值增量Δa满足

νt+Δt·Δt≤Δa≤νt·Δt，且

根据文献[11]可知，连续年金的现值微元为

da=νtdt

(7)

对微元式(7)在区间[0,n]上积分，即得连续年金的现值公式(6)。

连续付款n个计息期，每个计息期付款额之和为1的连续年金的终值[9]29为

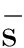
(8)

若时刻t支付这Δt单位，在时刻n的终值为(1+i)n-t·Δt；若时刻t+dt支付，在时刻n的终值为(1+i)n-t-Δt·Δt。这样，连续年金在[t,t+dt]上的终值增量Δs满足

(1+i)n-t-Δt·Δt≤Δs≤(1+i)n-t·Δt，且

由文献[11]可知，连续年金的终值微元为

ds=(1+i)n-tdt

(9)

对微元式(9)在区间[0,n]上积分，并令r=n-t作积分变换即得连续年金的终值公式(8)。

2.2 微元法计算生存年金的精算现值

以连续方式每年给付一单位的n年定期生存年金的精算现值为

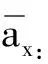
(10)

式中，ν为折现因子，tpx为x岁的人能活满n年的概率[9]72。

式(10)可由微元法推导而得。显然连续型生存年金的精算现值与被保险人的存活时间t有关，且t∈[0,n]，从中任取一子区间[t,t+dt]。因为每年支付一单位生存保险金，所以dt时间内给付Δt单位生存保险金。若时刻t支付这Δt单位，在保险签单时的精算现值为tEx·Δt；若时刻t+Δt支付，在保险签单时的精算现值为t+ΔtEx·Δt，这样，连续型生存年金在子区间[t,t+Δt]上的精算现值增量Δa满足

t+ΔtEx·Δt≤Δa≤tEx·Δt，且

根据文献[11]可知，一单位连续型n年定期生存年金的精算现值微元为

da=tEx·dt=νt·tpxdt

(11)

对微元式(11)在区间[0,n]上积分，即得一单位连续型n年定期生存年金的精算现值公式(10)。

2.3 微元法计算人寿保险的精算现值

死亡立即支付一单位保险金的n年定期寿险的精算现值为

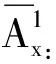
(12)

式中，fT(t)是x岁人的余命T的概率密度函数[9]48。

式(12)可由微元法推导而得。显然死亡给付的人寿保险的精算现值与被保险人的死亡时间t有关，且t∈[0,n]，从中任取一子区间[t,t+dt]。假设被保险人在时刻t+dt死亡，保险人立即支付的一单位死亡保险金在投保时的精算现值为νt+Δt·t|Δtqx，也即死亡即付一单位保险金的n年定期寿险在区间[t,t+dt]上的精算现值部分量ΔA=νt+Δt·t|Δtqx。因为

所以死亡即付一单位保险金的n年定期寿险的精算现值微元为

dA=νt·fT(t)dt

(13)

2.4 微元法计算人寿保险的责任准备金

全连续型全期缴费的n年定期寿险在x+t岁时的责任准备金未来法公式[9]121为

(14)

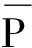
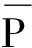
(15)

式中fU(u)为x+t岁的人的余命U的密度函数。对微元(15)式在区间[0,n-t]上积分，有

这刚好是全连续型全期缴费的n年定期寿险在x+t岁时的责任准备金未来法公式(14)。

3 结语

专业是大学人才培养的基本单位，课程是高等学校教学的基本单元，是高校教学的核心内容。将保险精算课程纳入数学与应用数学专业的课程体系，能够充实专业培养目标，优化学生专业知识结构，拓展学生金融应用能力，顺应金融经济发展潮流，符合学生多样化发展的需求。

本文基于“以匀代变，无限逼近”的微积分基本思想，一方面通过导数思想方法进一步阐述了利息强度和死力两个概念的本质内涵及其作用，另一方面通过微元法重新推导了固定年金的现值和终值公式、生存年金的精算现值公式、人寿保险的趸缴纯保费公式以及责任准备金的未来法公式，这种方法避免了厘定各种极易混淆的现金流的现值随机变量。实践表明，充分发挥数学与应用数学专业的优势背景，将微积分思想贯穿于保险精算的教学过程，有助于初学者准确把握精算概念，深刻理解现金流的动态折现或积累过程，从而逐渐形成精算数学思维，有效提高课程目标达成度。

[1]张德祥.高校一流学科建设的关系审视[J].教育研究，2016(8)：33-39，46.

[2]闫达文，宋立新，朱安妮.保险精算课程内容设置的研究[J].高师理科学刊，2013，30(8)：73-75.

[3]黄顺林.精算数学课程教学内容与教学方法的探索[J].科教文汇，2012(30)：88，95.

[4]闫达文，任立春，冯敬海.保险精算课程外延式教学的探索与实践[J].中国校外教育，2013(9)：316，318.

[5]刘春艳，麦拉苏.导入式教学法在寿险精算课程教学中的应用[J].中国管理信息化，2013，16(3)：98-99.

[6]孙佳美.精算类课程的实验教学探索[J].教育经济，2011(5)：59-60.

[7]陈辉，母丽华，蔡吉花,等.保险精算课程的实践教学研究[J].中国科教创新导刊，2012(22)：72.

[8]王达布希拉图.关于地方高校保险精算课程教学改革的思考[J].教学研究，2011，34(5)：61-63，67.

[9]李秀芳，傅安平，王静龙.保险精算[M].北京：中国人民大学出版社，2008.

[10]朱江红.关于利息力与死亡力[J].沧州师范学院学报，2014，30(1)：82-84.

[11]方涛.关于微元法的一个注记[J].上海工程技术大学学报，2015，29(2)：151-153.

责任编辑：周泽民

本刊声明

本刊自2005年4月起，加入台湾中文电子期刊服务—思博网(CEPS)。中文电子期刊服务—思博网是目前台湾地区最大的期刊全文数据库，其访问网址为http://www.ceps.com.tw。读者可以通过这一网址检索本刊2005年起各期的全文。

此外，由于本刊被CEPS收录，故凡向本刊投稿者均视为其文稿刊登后可供思博网(CEPS)收录、转载并上网发行；作者文章著作权使用费与稿费一次付清，本刊不再另付其他稿酬。如作者不同意文章被收录，请在投稿时告知本刊，本刊将进行适当处理。

谢谢合作！

Applications of Calculus Thought in Teaching ″Actuarial Science″ Course

YAO Jun

(Teaching Quality Evaluation Center，Changzhou Institute of Technology，Changzhou 213032)

Incorporating the course of actuarial science in the curriculum system for mathematics and applied mathematics specialty helps popularize actuarial education and meets students′ demand for diversified development.In order to better fulfill the course objective,calculus thought was integrated into the teaching process of actuarial science.The connotations of force of interest and fierce of mortality were elaborated from the angle of derivative definition.Some actuarial formulas of life insurance under continuous conditions were rederived by the infinitesimal method.

actuarial science；derivative； infinitesimal method； actuarial present value

10.3969/j.issn.1671- 0436.2017.02.017

2017- 03- 20

常州工学院课程建设项目(A3-4401-14-035)

姚俊(1979— )，男，硕士，讲师。

G642.0

B

1671- 0436(2017)02- 0082- 05