函数构造在数学分析解题中的应用
2017-08-01王跃超张聪于一丁
王跃超,张聪,于一丁
(吉林师范大学数学学院,吉林长春130103)
函数构造在数学分析解题中的应用
王跃超,张聪,于一丁
(吉林师范大学数学学院,吉林长春130103)
针对数学分析中一个重要的思想方法——函数构造法,从定义、方法以及应用三个方面进行讨论,归纳出多种构造函数的方法,同时列举出应用函数构造法解决数学分析中一些典型问题的实例,对其构造方法进行了总结。
函数构造;初等函数;解析函数;中值定理;积分上限函数
0 引言
函数构造在数学分析的学习与解题过程中有着重要的作用,也为其他后继课程的学习与理解提供了一种基本的思路和方法。函数构造是高等数学研究中一种十分重要的思想方法。函数构造的具体方法比较开放,没有固定的模式。因此,熟练掌握其方法并且灵活应用也有一定的难度。本文从数学分析研究过程中出现的一些相对典型并且比较常见的题目出发,给出函数构造的概念并对函数构造的方法进行了归纳与总结,将函数构造法分为初等方法和解析方法分别进行研究。再针对数学分析学习中最典型的两类问题,给出了函数构造在解题过程中的具体思路。
2006年,张剑锋、胡亚红[1]对函数构造在中值定理相关问题中的应用进行了研究。2010年,邹应奇[2]对多种构造法在数学分析解题中的应用进行了分析和比较。2014年,王建军[3]对函数构造法的教学技巧进行了探讨。本文从学习者的角度出发,针对数学分析中更基本更广泛的问题,用函数构造法进行了研究,突出了函数构造法的作用,探讨的内容更加全面。
1 函数构造
构造函数也常被称为辅助函数法,即在解决数学分析的有关问题时,根据题意的需要,在不违背题意的前提下,构造出能够解决问题的函数。
例1 设f(x)在[0,1]上连续,在(0,1)内可微,f′(x)>0(0 证明:令F(x)=f(1-x)f(x), 由于f(0)=0,则有 f(0)=F(1)=0。 由罗尔定理,存在λ∈(0,1),使 F′(λ)=0, 即 f′(λ)f(1-λ)-f(λ)f′(1-λ)=0。 令μ=1-λ,即有 f′(λ)f(μ)-f(λ)f′(μ)=0。由于f′(x)>0(0 故 f(x)>f(0)=0(0 则有 f(λ)f(μ)≠0。 因此,可解得 在上面的例子中,我们通过构造一个辅助函数将题中所给条件与要证明的结论联系了起来,从而将问题解决。这就是我们构造辅助函数的主要目的和意义。 2.1 初等方法 利用初等方法构造函数,是指根据题意通过构造一个初等函数来解决具体问题,主要包括构造复合函数、反函数和导函数等。这些方法在初等数学的学习过程中就已经开始接触,在数学分析解题的过程中还会经常用到。 则 (1) 又设 所以有 故F(x)单调增加,当x≥1时,有 F(x)≥F(1)>0 (2) 由式(1)、(2)可知,当x≥1时, f′(x)>0,f(x)也单调增加。 当x≥1时,有 f(x)≥f(1)=0, 即 故有 2.2 解析方法 利用解析方法构造函数,是指根据题意通过构造一个解析函数来解决具体问题,主要包括构造函数列和函数项级数,隐函数,积分上、下限函数,以及构造含参量的正常积分和非正常积分等。而想要通过构造解析函数来解决数学分析中的具体问题,就要熟练掌握这些函数的性质,尤其是解析性质。这是数学分析研究过程中的一个重要部分。 由题设可以验证F(t)在[0,1]上满足罗尔定理的三个条件,因此∃ξ∈[0,1],使F′(ξ)=0。 即 ξf(ξ)-2ξf(ξ)-ξ2f′(ξ)=0。 由此可解得 3.1 定积分中有关不等式的证明 在对定积分中的不等式进行证明时,我们通常会构造一个积分上限函数,并利用其性质解决实际问题。 例4 设f(x)、g(x)和它们的平方在[a,b]上可积,证明不等式 则当t≥a时,有 由此可知F(t)单调不减,又F(a)=0,所以F(b)≥0,即证 3.2 方程根的有关证明 在对方程的根的存在性进行证明时所采用的函数构造方法相对较灵活,主要根据题中所给条件以及所要证明的结论等特点来构造辅助函数,达到解题目的。 例5 证明:若f(x)在[a,b]上可微,f(x)=0的相邻两个根为α、β(a<α<β 证明:设F(x)=e-xf(x), 则F(x)在[α,β]上连续并可微,且 F(α)=F(β)=0。根据罗尔中值定理,∃ξ∈(α,β),使得F′(ξ)=0。 而 F′(ξ)=e-ξ[f′(ξ)-f(ξ)] 即 e-ξ[f′(ξ)-f(ξ)]=0。 故有 f′(ξ)-f(ξ)=0。 即ξ为f(x)-f′(x)=0的根,命题得证。 本文对函数构造在数学分析解题中的应用进行了初步探究与总结。通过对一些具体实例的分析给出了两种基本的函数构造方法,即初等方法和解析方法。同时给出了这两种方法在定积分中有关不等式的证明和在方程的根的有关证明中的具体应用,为相关问题的解决提供了基本的思路。 [1]张剑锋,胡亚红.浅谈构造函数法在数学解题中的应用[J].丽水学院学报,2006,28(2):71-74. [2]邹应奇.浅谈构造思想方法在数学分析中的应用[J].新课程学习(学术教育),2010(5):31. [3]王建军.从函数构造的整体观点谈数学分析教学[J].河西学院学报,2014,30(5):15-30. [4]王少英,王淑云.积分上限函数的性质及其应用[J].唐山师范学院学报,2008,30(6):20-22. [5]钱吉林.数学分析解题精粹[M].武汉:崇文书局,2009. [6]华东师范大学数学系.数学分析[M].4版.北京:高等教育出版社,2010. 责任编辑:周泽民 Application of Function Construction in Mathematical Analysis WANG Yuechao,ZHANG Cong,YU Yiding (College of Mathematics,Jilin Normal University,Changchun 130103) Function construction,an important way of thinking in mathematical analysis,was discussed from the aspects of definition,method and application.Methods of making constructors were summed up.Examples of typical problems in mathematical analysis were enumerated and the construction method was summarized. function construction;elementary function;analytic function;mean value theorem;integral upper limit function 10.3969/j.issn.1671- 0436.2017.02.018 2017- 01- 09 王跃超(1992— ),女,硕士研究生。 O174.4 B 1671- 0436(2017)02- 0087- 03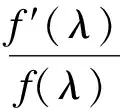
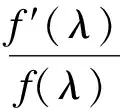
2 函数构造的常用方法








3 函数构造在数学分析解题中的典型应用


4 结语
