基于高维多目标优化的多车场车辆路径问题∗
2017-08-01毕志升郑炯彬蔡桂艳
毕志升 郑炯彬 蔡桂艳
(广州医科大学基础学院广州511436)
基于高维多目标优化的多车场车辆路径问题∗
毕志升 郑炯彬 蔡桂艳
(广州医科大学基础学院广州511436)
车辆路径问题是运筹学中著名的NP问题,在运输领域中具有重要的现实意义。多车场车辆路径问题是其中的一个重要分支,作为单目标优化问题和低维多目标优化问题被广泛研究。然而,多车场车辆路径问题本质上是一个高维多目标优化问题。因此,论文针对问题的本质,从物流企业和客户两个不同的角度考察四个优化目标,提出了基于高维多目标优化的多车场车辆路径问题,构造了相应的框架MO-MDVRP,并运用NSGA-III和I-DBEA得到了两个算法实例MD⁃VRP-NSGAIII和MDVRP-IDBEA。在六个Cordeau数据集上进行仿真实验,实验表明,运用MDVRP-NSGAIII和MDVRP-ID⁃BEA求解MO-MDVRP是可行的,MDVRP-NSGAIII的效果显著优于MDVRP-IDBEA。
车辆路径问题;多车场;高维多目标优化
Class NumberTP391
1 引言
电子商务的蓬勃发展为物流企业的发展提供了难得的机遇。然而,机遇背后是巨大的挑战。物流企业必须制定科学的运输路线,高效地满足客户的配送需求。这种运输路线的规划,对整个物流系统的运输效率、成本具有极其重要的影响。运输路线的规划可以抽象为车辆路径问题(Vehicle Rout⁃ing Problem,VRP)。VRP是运筹学中著名的NP问题,由Dantzig和Ramser[1]于1959年首次提出。它通过设计合理的车辆行驶路线,实现运输配送系统的运输成本最小化。
近年来,VRP受到越来越多国内外学者的关注。然而,已有的研究成果主要针对一个车场即单一配送中心的情况[2],而现实中许多物流企业建立了多个配送中心分布在不同的区域。因而,研究多车场车辆路径问题(Multiple Depot Vehicle Routing Problem,MDVRP)是十分必要的。
当前对MDVRP的研究主要基于单目标优化[2]和低维多目标优化[2~3]。然而,MDVRP本质上是一个目标数大于3的高维多目标优化问题。从物流企业的角度考虑,企业期望运输成本低、客户满意、各车辆服务工作量均衡或车场服务工作量比例满足特定要求;从客户的角度考虑,客户期望运输时间短。运输成本低,除了要求运输路径短,还需要车辆少司机少,以减少硬件成本和人工成本。但是,大量货物依赖少量车辆运输将导致货物积压,延长运输时间,引起客户不满。另一方面,每一件货物都用专车专人运输能达到运输时间短客户满意度高的要求,但也必然导致硬件成本和人工成本上升。从物流企业的生存和发展考虑,成本低和客户满意度高都是不可忽视的。因而,MDVRP中存在三个以上相互矛盾的目标。相比采用加权求和的方式将问题转化为单目标或低维多目标的求解方法,基于高维多目标优化求解MDVRP更符合问题本质和更具有理论意义。另一方面,基于高维多目标优化求解MDVRP能同时产生一组均衡解,反映目标间不同的取舍,有利于物流企业根据实际情况选择合适的实施方案。因而,基于高维多目标优化求解MDVRP是符合物流企业利益、具有现实意义的。
本文对MDVRP建立高维多目标优化模型MO-MDVRP,并运用非劣排序遗传算III(Nondom⁃inated Sorting Genetic Algorithm-III,NSGA-III)[4]和增强的基于分解的演化算法(Improved Decomposi⁃tion-Based Evolutionary Algorithm,I-DBEA)[5]进行求解。实验表明,NSGA-III和I-DBEA能有效求解MO-MDVRP。
2 多车场车辆路径问题
一般地,MDVRP可以定义为[6~7]:有M个车场,每个车场拥有K辆容量为Q、最大持续时间(包括路径行驶时间和客户服务时间)为D的车辆。有N个客户需要货物配送。客户i的货物容量为gi且gi<Q,该客户的服务时间为si且si<D。车场的服务时间为0。客户可以由任意车场的任意车辆服务,但只能被服务一次。在不超出容量和最大持续时间的情况下,每辆车一次离开车场可以为多个客户提供服务,服务结束后车辆必须返回原车场。
记节点{1,2,…,N}为客户节点;节点{N+1,N+2,…,N+M}为车场节点;mk为车场m的第k辆车;从节点i到节点j的距离为dij;R为一组满足约束的路径集合,对应问题的一个解。R中每一条路径都是一条以某一车场为起点,以同一车场为终点的环路。令

其中,i∈{1,2,…,N+M},j∈{1,2,…,N+M},k∈{1,2,…,K},且i和j不同时大于N。则MD⁃VRP可形式化描述为
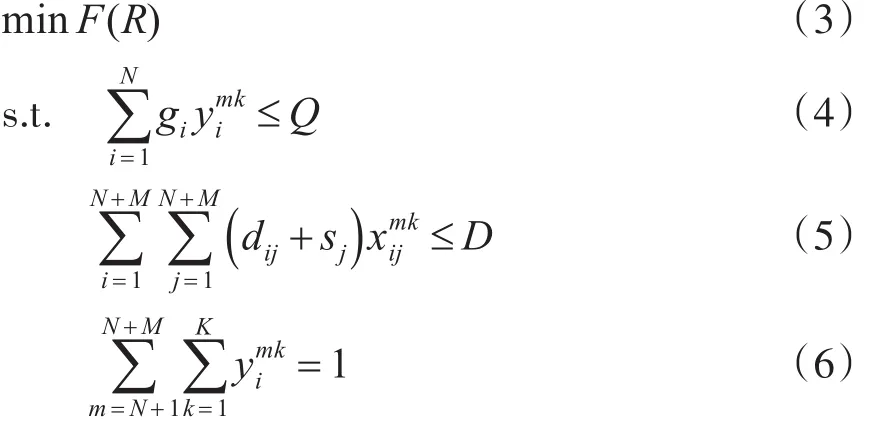
其中,F是目标函数,通常选择总持续时间或在其基础上结合车辆数等其他因素构造目标函数[2];式(4)是容量限制;式(5)是最大持续时间约束,这里用路径长度替代其中的路径行驶时间;式(6)是保证每个客户都被服务且仅被服务一次。显然,若所有客户的服务时间均为零,总持续时间等同于路径总长度。
近十年,MDVRP一直是一个研究热点。然而,在丰富的MDVRP研究成果中,近九成都把MDVRP作为一个单目标优化问题[2]。它们采用精确方法[8]、启发式方法[9]或原启发式方法[10]对MDVRP及其衍生的如带时间窗的MDVRP[11]、可拆分需求的MDVRP[12]等问题进行求解。在多目标优化方面,原启发式算法被普遍采用[2]。但它们都针对低维多目标优化,未充分考虑现实中常见的目标,具有一定的局限性。
3 基于高维多目标优化的多车场车辆路径问题
MDVRP本质上是一个高维多目标优化问题,从多目标优化的角度考察MDVRP是合理而且必要的。本节从目标函数设定、问题转换、编码、解码等方面描述基于多目标优化的MDVRP及其求解。
3.1 目标函数
从物流企业的角度考虑,本文设定总持续时间、车辆数、最大容量差各为一个优化目标;从客户的角度考虑,本文设定客户的等待时间为一个优化目标。因此,本文共设置四个目标函数。其中最大容量差定义为路径中实际载货容量的最大值和最小值之差。客户等待时间定义如下:
假设当前有一条路径r:0-3-2-4-0,节点0为车场,其余节点为客户。路径中第一个客户的等待时间为节点0和节点3之间的路径长度。相应地,第二个客户的等待时间为节点0到节点3、节点3到节点2的路径长度之和再加上节点3的服务时间。即,每个客户的等待时间是沿着路径从车场到客户之间的路径长度再加上之前经过的客户的服务时间。而优化目标则是最小化所有客户的等待时间之和。记R中路径数量为|R|,每一条路径上的客户等待时间为wr。则R中客户等待时间为
故,该MDVRP可形式化描述如下:

其中,Km≤K是第m个车场实际派出的车辆数;式(7)是最小化总持续时间;式(8)是最小化车辆数;式(9)是最小化最大容量差;式(10)是最小化客户等待时间。问题约束如第2节所述。
3.2 问题转换
鉴于传统单车场VRP的丰硕成果,求解MD⁃VRP可以先采用特殊的转换方法把问题转化为单车场VRP,然后用单车场VRP的求解方法进行求解。转换方法通常有两类[13]:聚类和虚拟车场。前者通过对车场和客户进行聚类,将一个车场和部分客户划分到一个聚类中,然后在聚类内求解VRP。后者使用一个虚拟车场代替实际车场进行路径规划,并在路径规划结束后,将路径划分到使路径总长度最小的实际车场中。
在高维多目标背景下,总持续时间已经不是唯一的目标,而聚类的划分蕴含了距离的因素,偏向于优化总持续时间。由于目标间存在矛盾,这种偏向不利于其它目标的优化。因此,本文选择虚拟车场的方式进行问题转换。
根据文献[14],采用设置虚拟车场的方式将MDVRP转换为单车场VRP。具体方法是:先设置一个虚拟车场,让所有车辆都从虚拟车场出发并在服务结束后回到虚拟车场。如此,MDVRP被转换成单车场VRP。然后采用针对单车场VRP的方法求解。如图1所示,假设有15个客户和4个车场,在增加虚拟车场O后转换成单车场VRP并进行路径规划。
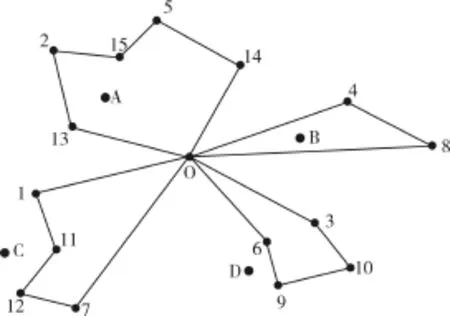
图1转化后进行路径规划
在路径划分之后需要把实际车场添加到各条路径中。添加的方法是:遍历每条路径,在尚有空余车辆的车场中选择令总持续时间最小的车场替换虚拟车场。这是一种贪心策略,在所有车场都有空余车辆的情况下,这种方法保证添加后总持续时间最小;当存在个别车场没有空余车辆时,可能陷入局部最优。而且,这种替换方法对路径的替换顺序敏感。
3.3 染色体编码
本文采用长度为N的整型数组对染色体进行编码。数组以客户的编号作为数组的元素,每个编号出现且仅出现一次。记chrom为一条长度为N的染色体,chrom[i]为其中的第i个元素。直观地,这种编码的染色体可以通过将各个路径中的客户按路径顺序连接后得到。如图1所示的路径可以通过chrom={13,2,15,5,14,4,8,3,10,9,6,7,12,11,1}表示。因而,一条染色体就是问题的一个解。由于没有参杂车场节点,对任意给定的MD⁃VRP,其染色体长度固定,为算法的搜索带来便利。然而,这种编码方式并没有记录车场和路径划分信息,因而需要额外的解码技术,以便将染色体重新划分为一组路径。
3.4 染色体解码
本文在文献[13]的Plot算法基础上添加持续服务时间约束,得到Plot+算法,以满足MDVRP的问题约束。本文采用Plot+算法对染色体进行解码,算法如图2所示。
在解码前,首先在chrom首位插入一个0节点。在Plot+中,v[i-1]保存的是从车场开始到客户chrom[i-1]为止路径的总长度(Line 7)。chrom[i-1]是上一路径的最后一个客户节点。cost对应的是以客户chrom[i]为第一个客户、以客户chrom[j]为最后一个客户的路径长度,是当前尝试构造的路径(Line 5)。这种尝试直到不满足约束或没有客户为止(Line 13)。Line 8中if为真,则构造一条以客户chrom[i]作为第一个客户节点,以客户chrom[j]为最后一个客户节点的路径。此时意味着新路径较原方案(对应v[j])的总持续时间更小,或路径等长但能使前一条路径服务更多的客户,即车辆容量的利用更充分。如果if为假,意味着原方案更优,并在下一次循环(Line 4-Line 13)中尝试构造以chrom[j+1]作为最后一个客户节点的路径。pred保存当前节点的路径是从chrom中哪一个客户开始的(Line 9)。若pred[j]=x,说明客户chrom[j]所在的路径是从客户chrom[x+1]开始的。因此,当算法结束时,从后向前读取数组pred,就可以实现路径的划分。例如chrom={0,2,5,1,3,4},pred={0,0,0,1,1,2}。从后向前读取数组pred,pred[5]=2,即当前最后一个客户chrom[4]所在的路径是从chrom[2+1]开始,即得到路径0-1-3-4-0,0为虚拟车场。继续读取pred,pred[2]=0,即当前最后一个客户chrom[2]所在的路径是从chrom[0+1]开始的,得到路径0-2-5-0。至此,解码结束。
算法1:Plot+算法
输入:待解码的染色体chrom,客户数量N.
1.chrom插入0节点,新建数组v,其中v[0]=0,其余元素赋值为正无穷,新建前缀数组pred,每一个元素赋值为0;
2.fori=1 to N
3.j=i,令当前容量load为0,持续服务时间cost为0;
4.do
5.读取chrom[j],更新load和cost;
6.if load和cost不违反约束
7.vNew=v[i-1]+cost;
8.if vNew<v[j]或((vNew=v[j])
且(pred[i-1]+1<pred[j]))
9.更新v[j]=vNew,pred[j]=i-1;
10.end if
11.j=j+1;
12.end if
13.while load和cost满足约束且j≤N;
14.end for
输出:前缀数组pred.
对解码后得到的每一条路径,尝试在当前尚有空余车辆的车场中选择令总持续时间最小的车场替换虚拟车场。
3.5 基于高维多目标优化算法求解多车场车辆路径问题
基于高维多目标优化算法求解MDVRP的框架如图3所示。
MO-MDVRP对高维多目标优化算法的选择并不敏感,除了极其有限的额外操作(Line 4),并没有对所选的算法有任何修改。因此,MO-MDVRP是一个通用的基于高维多目标优化求解MDVRP的框架。
算法2:MO-MDVRP
输入:客户集合Cus,车场集合Dep,算法终止条件condition.
1.生成初始解集,形成初始种群;
2.dO
3.运用选定的高维多目标优化算法对当前种群进行演化;
4.对演化得到的个体进行解码、评价;
5.根据所选的高维多目标优化算法和上一步的评价结果,生成下一代种群;
6.until满足condition
输出:最后一代种群.
本文采用NSGA-III[4]和I-DBEA[5]求解MO-MDVRP。NSGA-III是经典的高维多目标优化算法,而I-DBEA是近期发表的高维多目标优化算法。两者在求解高维多目标优化问题上都有出色的效果。关于多目标优化算法的详细描述可参见文献[14],这里不再详述。
4 仿真实验
本节选择NSGA-III[4]和I-DBEA[5]构造MOMDVRP的实例,分别命名为MDVRP-NSGAIII和MDVRP-IDBEA,并进行仿真实验测试算法效果。
4.1 测试平台
本文以MOEAFramework为实验平台,它是一个用于开发和测试多目标优化算法的开源平台,提供了丰富的算法和测试接口。本实验在平台上对MO-MDVRP进行编码并调用平台的NSGA-III和I-DBEA进行问题求解。由于染色体的整型数组编码和客户编号不可遗漏不可重复,NSGAIII和ID⁃BEA均选用PMX[15]作为交叉算子,并使用随机插入算子和随机交换算子作为变异算子。
本实验的实验环境是MOEA Framework 2.11;JDK 8;CPU 2.3GHz;16GB RAM。
4.2 数据集及参数设置
本实验的数据集来自University of Malaga的Networking and Emerging Optimization研究组。该研究组持续研究各种VRP,并提供了一系列MD⁃VRP数据集。实验在6个Cordeau数据集上进行,数据集的基本参数如表1所示。
实验中,MDVRP-NSGAIII和MDVRP-IDBEA的最大评价次数均为106,PMX的交叉分布指数(Distribution Index)为20,随机插入算子和随机交换算子的概率均为0.3,其余参数取建议值[4~5]。
4.3 性能指标
本文选择了2个常用的性能指标对MD⁃VRP-NSGAIII和MDVRP-IDBEA的运算结果进行比较。

表1 测试集的基本参数
1)逆世代距离(Inverted Generational Dis⁃tance,IGD)[16]:IGD通过度量算法求得的Pareto前沿与真实Pareto前沿的距离评价算法的优劣,是一个同时度量Pareto最优解集的收敛性和多样性的指标。指标值越小越好。
2)超体积(Hypervolume,HV)[17]:HV通过Pa⁃reto最优解集在空间中与参考点围成的空间大小度量算法的优劣,同样是一个同时度量Pareto最优解集的收敛性和多样性的指标。指标值越大越好。
对算法的各性能指标值进行显著性检验,显著性水平为0.05。
4.4 实验结果
实验中,每个算法在每个数据集上独立运行30次,运行后的结果如表2、表3及图2~图7所示。加粗底纹表示该结果显著优于其它对比算法。

表2 各算法在p01-p06上运行30次IGD和HV比较
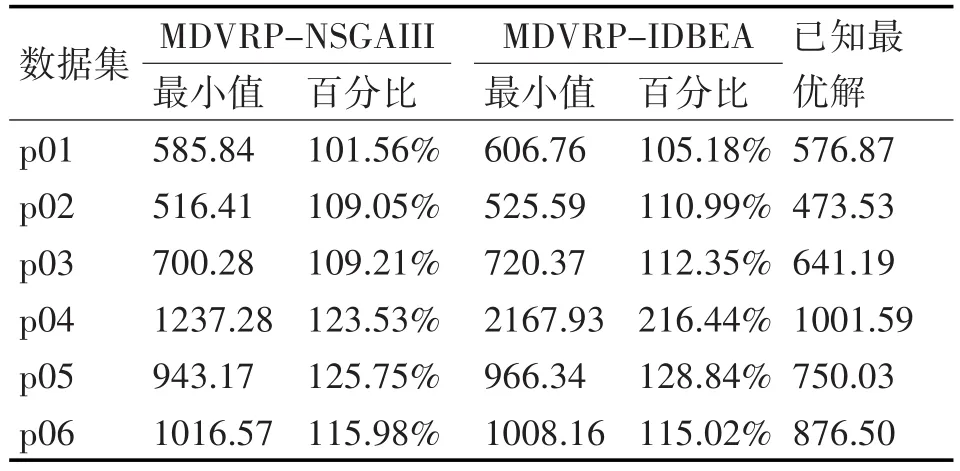
表3 在p01-p06上运行30次的f1最小值与已知最优解比较
从表2可知,在IGD指标上,MDVRP-NSGAIII较MDVRP-IDBEA有明显的优势,在2/3的数据集上显著地优于后者。而在HV指标上,除了p02上MDVRP-NSGAIII更优以及p03、p05上MD⁃VRP-IDBEA更优,其余数据集上两者并没有显著的差异。从p03可以看出,不同的指标可能对Pare⁃to最优解集的优劣给出截然不同甚至矛盾的评价。因而,通过多个指标考察算法性能是十分必要的。图2~图7给出了p01-p06目标间两两组组合的Pareto前沿。直观地,在多数情况下MD⁃VRP-NSGAIII(灰色)比MDVRP-IDBEA(黑色)更靠近坐标系左下角,意味着MDVRP-NSGAIII较MDVRP-IDBEA更优。这与表2的结果一致。
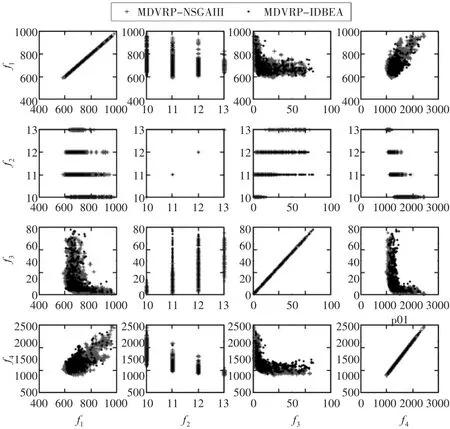
图2p01的Pareto前沿
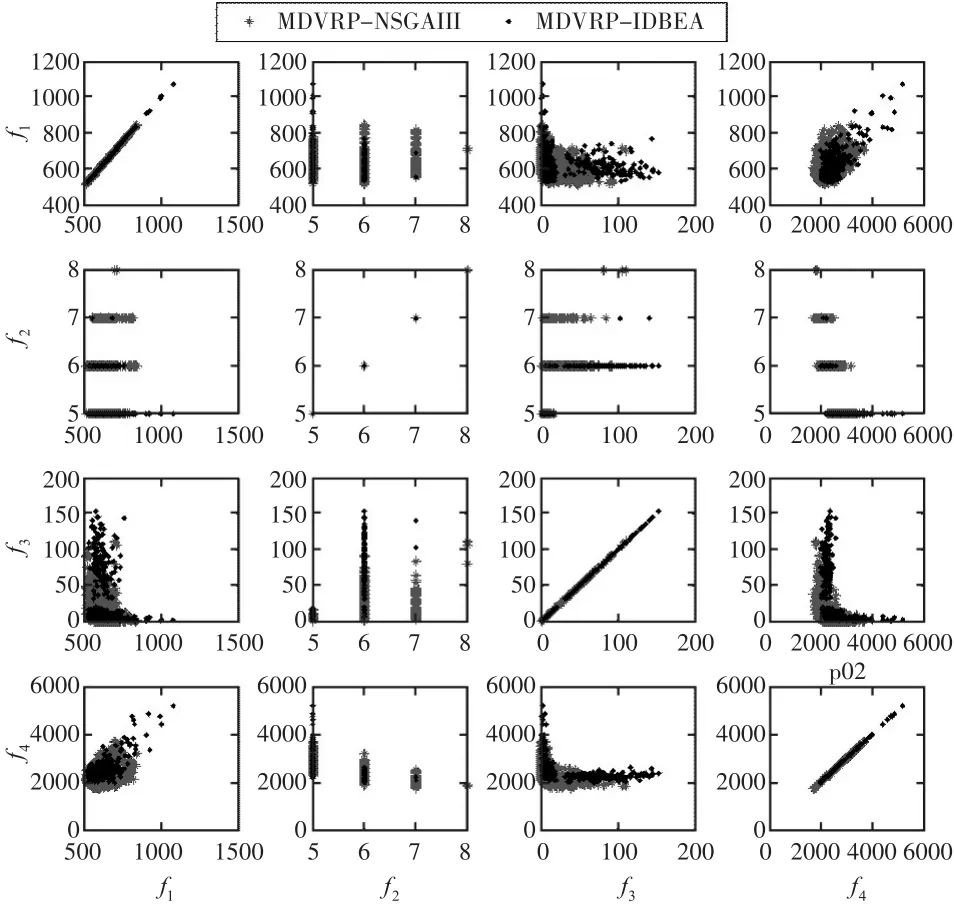
图3p02的Pareto前沿

图4p03的Pareto前沿
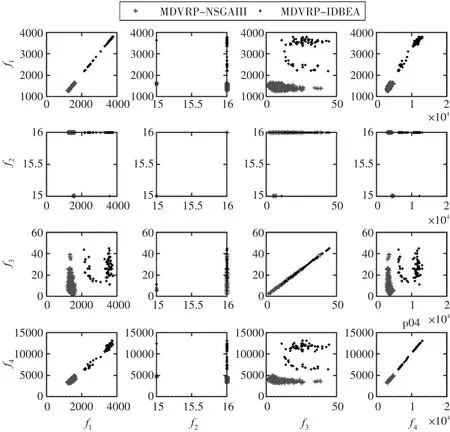
图5p04的Pareto前沿

图6p05的Pareto前沿
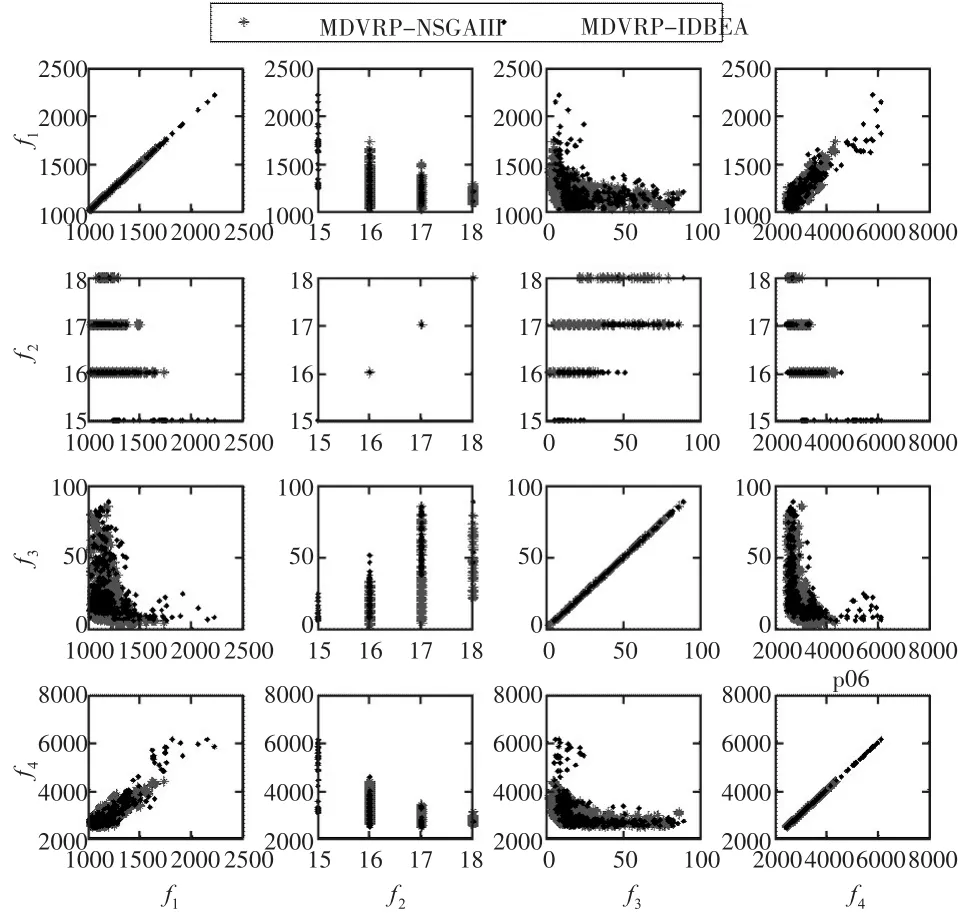
图7p06的Pareto前沿
表3给出了算法在f1(即路径总长度)上找到的最小值、数据集给出的已知最优解以及两者的比值。首先,数据集并没有说明已知最优解的来源,而不同类算法的结果直接比较是不合适的。此外,MDVRP-NSGAIII和MDVRP-IDBEA并没有单独优化f1,而是同时优化四个目标函数,得到的是目标间的均衡。因此不能因为没有得到已知最优解而否定MDVRP-NSGAIII和MDVRP-IDBEA。虽然不能直接比较,但是依然可以通过已知最优解对MD⁃VRP-NSGAIII和MDVRP-IDBEA的搜索能力进行讨论。在规模较小的p01,MDVRP-NSGAIII和MD⁃VRP-IDBEA得到非常接近已知最优解的结果。随着车辆数、客户数的增加,两种算法的结果与已知最优解的差距都有一定程度的上升。这说明,MD⁃VRP-NSGAIII和MDVRP-IDBEA具有一定的求解高维多目标MDVRP的能力。但是,当问题越发复杂,算法至少在f1极端解的搜索上会显得不足。这是因为,无论是NSGAIII还是IDBEA都没有专门的搜索机制对问题的极端解进行搜索。而对多目标优化问题而言,表3中的已知最优解就是问题的极端解。这意味着,要得到更接近已知最优解的结果,不能单独依靠高维多目标优化算法自己的搜索能力。局部搜索算子,甚至是针对特定目标函数的局部搜索算子会变得不可或缺。事实上,极端解的更新是有可能推动整个种群的进化、促进Pareto前沿推进的。因此,通过引入局部搜索算子提高算法搜索能力是值得尝试的。由于数据集并未给出其它目标上的已知最优解,因此没有对其它目标值进行比较。
5 结语
针对MDVRP的高维多目标本质,本文构造了基于高维多目标优化的MDVRP框架MO-MDVRP,并运用NSGA-III和I-DBEA得到两个算法实例MDVRP-NSGAIII和MDVRP-IDBEA。实验表明,MDVRP-NSGAIII和MDVRP-IDBEA求解MO-MD⁃VRP是可行的;在IGD指标上,MDVRP-NSGAIII较MDVRP-IDBEA具有明显的优势。
MO-MDVRP并没有引入任何的局部搜索算子。通过引入局部搜索算子提高算法搜索能力是值得尝试的。然而,正如不同的性能指标对算法评价不同,不同的局部搜索算子对各个目标函数的影响可能也大相径庭。如何设计局部搜索算子以便最大限度地提高算法的搜索能力是后续研究中需要解决的问题。
[1]G Dantzig,J Ramser.The truck dispatching problem[J]. Management Science,1959,6(8):80-91.
[2]J R Montoya-Torres,J L Franco,S N Isaza,H F Jiménez,N Herazo-Padilla.A literature review on the vehicle rout⁃ing problem with multiple depots[J].Computers&Indus⁃trial Engineering,2015,79:115-129.
[3]R Tavakkoli-Moghaddam,A Makui,Z Mazloomi.A new integrated mathematical model for a bi-objective multi-de⁃pot location-routing problem solved by a multi-objective scatter search algorithm[J].Journal of Manufacturing Sys⁃tems,2010,29(2):111-119.
[4]K Deb,H Jain.An evolutionary many-objective optimiza⁃tion algorithm using reference-point-based nondominated sorting approach,part I:Solving problems with box con⁃straints[J].IEEE Transactions on Evolutionary Computa⁃tion,2014,18(4):577-601.
[5]M Asafuddoula,T Ray,R Sarker.A decomposition-based evolutionary algorithm for many-objective optimization[J].IEEE Transaction on Evolutionary Computation,2015,19(3):445-460.
[6]L Calvet,A Ferrer,M I Gomes,A A Juan,D Masip.Com⁃bining statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmen⁃tation[J].Computers&Industrial Engineering,2016,94:93-104.
[7]J W Escobar,R Linfati,P Toth,M G Baldoquin.A hybrid granular tabu search algorithm for the multi-depot vehicle routing problem[J].Journal of Heuristics,2014,20(5):483-509.
[8]S Ray,A Soeanu,J Berger,M Debbabi.The multi-depot split-delivery vehicle routing problem:Model and solu⁃tion algorithm[J].Knowledge-Based Systems,2014,71:238-265.
[9]A Rahimi-Vahed,T G Crainic,M Gendreau,W Rei. Fleet-sizing for multi-depot and periodic vehicle routing problems using a modular heuristic algorithm[J].Comput⁃ers&Operations Research,2015,53:9-23.
[10]T Vidal,T G Crainic,M Gendreau,C Prins.Implicit de⁃pot assignments and rotations in vehicle routing heuristics[J].European Journal of Operational Research,2014,237(1):15-28.
[11]J Li,Y Li,P M Pardalos.Multi-depot vehicle routing problem with time windows under shared depot resources[J].Journal of Combinatorial Optimization,2014,31(2):515-532.
[12]R Liu,Z Jiang,R Y K Fung,F Chen,X Liu.Two-phaseheuristic algorithms for full truckloads multi-depot ca⁃pacitated vehicle routing problem in carrier collaboration[J].Computers&Operations Research,2010,37(5):950-959.
[13]邓欣.基于遗传算法的多车场车辆路径问题研究[D].重庆:重庆大学,2007. GENG Xin.Research on Multiple Depot Vehicle Routing Problem Based on Genetic Algorithm[D].Chongqing:Chongqing University,2007.
[14]公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009,20(2):271-289. GONG Maoguo,JIAO Licheng,YANG Dongdong,et al. Research on Evolutionary Multi-Objective Optimization Algorithms[J].Journal of Software,2009,20(2):271-289.
[15]D E Goldberg,Jr R Lingle.Alleles,loci,and the travel⁃ing salesman problem[C]//Proceedings of the 1st Interna⁃tional Conference on Genetic Algorithms,154-159.
[16]Q Zhang,H Li.MOEA/D:A multiobjective evolutionary algorithm based on decomposition[J].IEEE Trans.on Evolutionary Computation,2007,11(6):712-731.
[17]M L E,Zitzler,L Thiele.SPEA2:Improving the strength pareto evolutionary algorithm[C]//Evolutionary Methods for Design,Optimization and Control with Applications to Industrial Problems,K Giannakoglou,D T Tsahalis,J Periaux,K D Papailiou,T Fogarty,Eds.,2002,95-100.
Multiple Depot Vehicle Routing Problem Based on Many-Objective Optimization
BI ZhishengZHENG JiongbinCAI Guiyan
(School of Basic Science,Guangzhou Medical University,Guangzhou511436)
Vehicle routing problem is a well-known NP problem in operations research,which has important practical signifi⁃cance in transportation field.As one of the important branches,multi-depot vehicle routing problem has been widely studied as a single-objective optimization problem and a multi-objective optimization problem.However,multi-depot vehicle routing problem is essentially a many-objective optimization problem.Therefore,in view of the nature of the problem,four optimization functions are inspected from the view of logistics enterprise and customer.Next,multi-depot vehicle routing problem based on many-objective op⁃timization is proposed.Then,a framework called MO-MDVRP is constructed for this problem.After that,instances of this frame⁃work based on NSGA-III and I-DBEA are proposed,namely MDVRP-NSGAIII and MDVRP-IDBEA.The algorithms are tests on six Cordeau datasets.The experiments show that MDVRP-NSGAIII and MDVRP-IDBEA are feasible in solving MO-MDVRP.And MDVRP-NSGAIII is more effective than MDVRP-IDBEA in these datasets.
vehicle routing problem,multi-depot,many-objective optimization
TP391
10.3969/j.issn.1672-9722.2017.07.013
2017年1月5日,
2017年2月11日
国家自然科学基金(编号:61603106);广州市市属高校科研项目(编号:1201630320);广州市教育科学规划课题(编号:1201553242);广州医科大学科学科研项目(编号:L135042)资助。
毕志升,男,博士,讲师,研究方向:计算智能和数据挖掘。郑炯彬,男,硕士研究生,研究方向:数据挖掘。蔡桂艳,女,硕士,讲师,研究方向:数据挖掘。
