以计算思维为切入点的递归算法教学改革
2017-07-31朱君波龚沛曾杨志强
朱君波+龚沛曾+杨志强

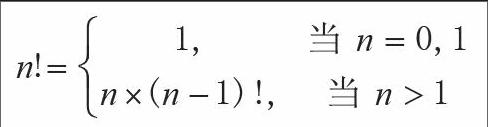
摘 要:程序设计课程是培养学生计算思维能力的重要课程,其中的递归算法设计体现了计算思维中问题分解、抽象和自动化的本质。文章提出以计算思维为切入点进行教学改革,围绕计算思维的能力培养,重新整理递归教学内容,改革教学方法,变知识的教学为思维的训练。
关键词:计算思维;程序设计;递归算法;教学改革
文章编号:1672-5913(2017)07-0030-04
中图分类号:G642
0 引 言
递归函数(过程)是在其定义中直接或间接调用自身的一种函数(过程)。通过设计递归函数(过程)来解决问题的算法就是递归算法。递归算法的设计思想是分治思想的典型代表,利用递归算法编写的程序具有结构简单清晰、可读性强的特点。许多复杂的问题都可以通过递归算法来简化,以简单的形式得出结果。
2010年11月,陈国良院士在第六届大学计算机课程报告论坛上,第一次正式提出将“计算思维能力培养”作为计算机基础课程教学改革的切入点 [1]。随后教育部高教司设立了以计算思维为切入点的大学计算机课程改革项目[2]。
在大学计算机的教学中,程序设计课程是培养学生计算思维能力的有效途径[3]。递归是程序设计课程中固有的内容,也是教学难点。如何让非计算机专业学生(尤其是非理工类的学生)理解递归、利用递归算法求解问题,是教学中面临的新问题[4]。
1 传统的递归教学
在传统的递归教学中,教师往往将重点放在递归算法的解释上,而教学方法则采用“介绍—举例—演示”三步曲教学法。一般以求阶乘的典型例子作为介绍,然后通过一些具有数学上很直观的递归函数,如斐波那契数列作为举例,最后演示经典的“汉诺塔”问题作为结束。
在这种教学方法中,教师仅针对问题解释递归算法,学生从表面上看程序代码只有寥寥数行,看似简单,但递归如何执行,学生并不了解,觉得很悬乎;同时学生对现有的例子又感觉没有实际应用价值。
在以计算思维为切入点的教学改革实施以来,我们认识到递归算法解决问题的重要性。传统的递归教学在宏观上没有掌握递归的精髓——问题的分解、抽象和自动化;在微观上没有从递归的执行过程分析。学生学习时听得云里雾里,更不要说让学生自己设计一个递归函数(过程)去解决实际问题了;教师也仅仅完成了教学要求,以至于在学时压缩的情况下这部分内容也自然而然地被删除了。
2 递归教学的新认识
利用计算思维的方法设计递归,首先理解什么是递归现象?递归的核心思想是什么?如何理解递归的执行过程?如何利用计算思维的方法设计递归算法?
2.1 认识递归现象
首先从日常生活中遇到的递归现象开始。在图1中,两面镜中产生一连串的“像中像”;也可以从大家熟悉的“老和尚给小和尚讲故事”“阿凡提和国王下棋赏麦粒”等故事开始。通过这些常见递归现象的展示,让学生对递归有个感性认识。
其次,通过展示递归数学公式,让学生对递归函数的实现有所了解。这里可以引用学生熟悉的求n阶乘公式:
并给出其对应的递归函数(程序代码使用VB.NET编写):
Function f#(ByVal n% )
If ( n < 2 ) Then
f=1
Else
f=n*f(n-1)
End If
End Function
2.2 递归核心思想
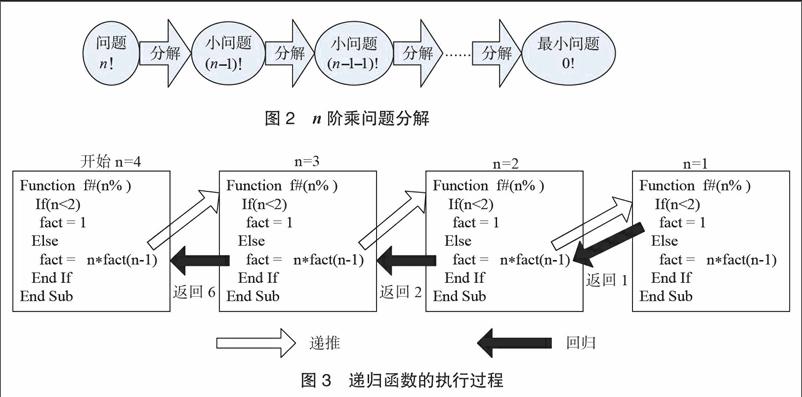
通过认识递归现象,引导学生理解递归的实质是“分而治之”“大问题分解为本质相同的小问题”的思想,如图2所示。问题分解是计算思维的典型方法,也是递归算法的核心思想,应贯穿于分析和设计递归函数的始终。
2.3 递归的执行过程
递推和回归是递归执行过程的两个基本要素。递推是从大问题到小问题,等待小问题的答案,回归是小问题返回给大问题答案。图3以n阶乘递归函数计算4阶乘为例,示意递归的执行过程。
计算机在执行递归的過程中,递推和回归的过程是利用栈来实现的。栈是计算机中特殊的存储区,主要功能是暂时存放数据和地址。栈的特点是先进后出,它有压栈和弹出两个基本操作。每一次的递推过程实质是压栈操作,将函数的参数、变量和返回地址等数据保存在栈中。每一次回归的过程就是栈的弹出操作,将栈中保存的数据释放。
2.4 利用计算思维的方法设计递归算法
设计递归算法的关键是要根据具体的问题,通过分解抽象出递归模式,再利用计算机本身的函数调用机制实现自动化。这种分解、抽象和自动化的方法正是计算思维的本质。
3 以递归模式为中心的递归算法设计
以递归模式为中心的递归算法设计分成3个步骤:问题分解、抽象和自动化。
3.1 问题分解
问题分解就是将大的、复杂的问题分解为本质相同的、规模较小的问题,当小问题解决,那么大问题也解决了。而规模较小的问题,因为本质上是和大问题相同的,可以用同样的方法继续分解为规模更小的子问题。这样通过一系列的分解,最后分解到能直接给出结果的最小问题,然后再逐渐返回,最终大问题得以解决。
在问题分解中,需要注意两点:一是分解后的小问题的规模要变小,例如n阶乘的小问题是n-1的阶乘,它的规模更小,而不是规模更大的n+1;二是问题小到一定程度时不能再小,直接得出结果,例如阶乘,当n=1时不能再小了,得出结果是1。
3.2 抽 象
根据问题分解的结果,正确地将大问题和多个小问题之间的逻辑关系表达出来,变成递归模式。递归模式就是小问题与大问题之间的逻辑关系,即大问题是如何随着小问题的解决而完成的?
这里有3种情况:第一种是逻辑或的关系,只要其中一个小问题解决,则大问题解决。例如,n阶乘问题,分解成数字n和n-1的阶乘,只要n-1阶乘解决则n阶乘解决。第二种是逻辑与的关系,多个小问题都要解决,但与小问题解决的先后顺序无关,如斐波那契数列。第三种也是逻辑与的关系,但与多个小问题的解决顺序是有关联的,如数组排序问题。
3.3 自动化
得到了递归模式之后,根据程序设计语言,编写相应的递归函数就能实现递归算法了。递归算法自动化的實现,本质是利用计算机本身的函数调用机制。计算机的函数调用机制就是函数调用栈,它的压栈操作就是递推,它的弹出操作就是回归。
4 递归案例
设计合理的教学案例是保证良好教学的关键。一个成功的教学案例可以丰富课堂内容,活跃课堂气氛,激发学生的积极性,促进教师与学生的互动。
在递归的教学过程中,教师常常觉得案例不够丰富,这也是困扰教学的一个问题。其实递归的案例无处不在,只要细心去挖掘,程序设计中常见的算法都可以成为递归的案例。将这些算法按照数据类型进行简单的归类,即整数处理、字符串处理和数组处理等,同类的问题具有相似的问题分解方法和递归模式。
4.1 整数处理
整数处理类的常见问题有最大公约数、整数位数和数制转换等。这类案例的递归算法设计过程如下:首先通过整除和取余,将被处理的整数分解成商和余数;其次建立被除数、商和余数的逻辑关系,抽象出递归模式;最后,通过函数定义,将递归模式编写成递归算法。
我们以求整数m的位数为例,分析整数的递归算法设计。第一步,将被除数m除以10,分解成商(m\10)和余数。商也是个整数也有位数,可以用同样的方法继续分解,当商为0,则m是1位数,是最小问题,不再分解。
第二步,抽象出递归模式。被除数m(大问题)和商m\10(小问题)与余数(小问题)的逻辑关系是:m的位数等于商的位数+1,与余数无关。属于第一种递归模式,只要得到商的位数(递归调用获得),则被除数的位数也将获得,得到如下递归模式:
第三步,根据递归模式编写递归函数:
Function fig%(ByVal m%)
If m \ 10 = 0 Then
fig = 1
Else
fig = fig(m \ 10) + 1
End If
End Function
4.2 字符串处理
字符串类问题的分解一般如下:将一个字符串按照位置分成一个字母(第一个或最后一个)和去除一个字母后的子串。子串比原先的字符串个数少、规模小,而且它也可以用相同的方法继续分解。当字符串的长度为0时,这是最小问题,不能再分解了。
例如,将字符串中的数字字符提取出来,组成新的数字子串。如字符串“d1d8ffd76yu9” 提取出数字字符串“18769”。
第一步,将字符串s分解成第一个字母(用c表示)和后面的子串(s1=mid(s,2))。当字符串长度为0时,这是最小问题,不能再分解。
第二步,抽象出递归模式,s的数字串就是c和s1的数字串的连接。属于递归模式中的第二种情况,两个子问题都要解决。c的数字子串就是判断c是否为数字字符。s1的数字子串通过递归调用获得。因此,得到如图4所示的递归模式。
第三步,根据递归模式编写递归函数代码。程序代码相对简单,不再赘述。
4.3 数组处理
数组的处理一般是通过循环实现的,碰到复杂的操作,如排序,则要进行多重循环。在学生循环概念薄弱的情况下,多重循环将是学生的噩梦。
数组的分解方法和字符串有点类似:按照位置(下标)将数组分解成一个位置(第一个或最后一个)和其余位置的子数组。每次分解后会减少一个位置,规模越来越小;当数组下标上界为0(数组长度为1)时,不再分解。
例如,将数组a中的0~n个数进行按位置(下标)递增排序,递归的排序过程名设为sort(a,n)。第一步,将数组a(n)分解成两部分:0~n-1的子数组和第n个元素,如图5所示。这样将a(n)的排序就分解成了a(n-1)的排序和第n个位置数据的确定了。a(n-1)的排序可以用同样的方法继续分解,当n=0是最小问题。
第二步,按照前面的分解,整个排序就是两个步骤:先是第n个位置数据的确定,然后是0~n-1的子数组排序(递归调用sort(a,n-1)实现),得到如图6递归模式。这种递归模式属于第三种情况,子问题的解决先后顺序是有关系的。
第三步,根据递归模式编写相应的程序代码。
需要注意的是,在第三种递归模式中,多个子问题的解决顺序是有关联的。上面的方法是先解决最后一个位置,再解决子数组的排序。还有一种方法是先解决子数组的排序,再确定最后一个位置的数据。读者可以试着用这一种方法设计递归算法。
进一步拓宽学生的思路,换一种分解方法,将第一个位置分离出来,递归模式也是属于第三种情况。
5 结 语
将计算思维引入到递归算法的教学中来,在不改变教学内容的基础上,改进教学方法,有意识地将与计算思维相关的问题分解、抽象和自动化的方法自然地融入到教学中,使原有的教学活动上升到计算思维的新高度。
在递归教学中引入计算思维,不是在原有内容上贴上计算思维标签,将所有的迭代算法用递归算法代替;而是提炼并展现隐藏在这些算法设计后面的计算思维方法,引起学生学习兴趣和心理共鸣。
在递归算法的教学中利用递归模式降低教学难度。使原先学生难以理解、教师经常弱化的递归教学变得容易,教师也不再忐忑不安。从宏观上分析问题,通过分解,抽象出递归模式,无论对理工类还是文科类的学生都很容易接受。
通过教学方法的改革,同时也拓展了课程的深度。将学生学习过的算法修改成递归的算法,再与原来的算法进行比较,更容易引发学生的学习兴趣。教师引导学生将递归算法和迭代算法进行比较,使学生对递归和迭代这两种算法有更深入的理解,不仅巩固了学到的知识,更重要的是提升了学生分析问题、解决问题的能力。
参考文献:
[1] 陈国良, 董荣胜. 计算思维与大学计算机基础教育[J]. 中国大学教学, 2011(1): 7-11.
[2] 李廉. 计算思维: 概念与挑战[J]. 中国大学教学, 2012(1): 7-12.
[3] 龚沛曾, 杨志强. 大学计算机基础教学中的计算思维培养育[J]. 中国大学教学, 2012(5): 51-54.
[4] 冯博琴. 对于计算思维能力培养“落地”问题的探讨[J]. 中国大学教学, 2012(9): 6-9.
(编辑:彭远红)
