某一类三阶非线性方程的三点线性边值问题

王国灿

(大连交通大学 理学院，辽宁 大连 116028)

某一类三阶非线性方程的三点线性边值问题

王国灿

(大连交通大学 理学院，辽宁 大连 116028)

利用积分算子与上下解方法，研究了某一类三阶非线性方程的三点线性边值问题，得到了其解的存在性与唯一性.另外，在恰当的条件下，通过构造具体的上下解，证明了结论的应用性.

非线性三阶方程;线性三点边值;存在性与唯一性;上下解

0 引言

在工程物理上有重要应用，而且在流体力学中有重要意义的三阶非线性常微分方程边值问题，文献[1- 8]及其所列参考文献已经做过不少研究，但以往的工作主要局限于特殊的非线性方程及简单三点边界条件，至于解的唯一性问题，只见到几篇文献[1，5].本文利用上下解方法，考虑下列一般的三阶非线性微分方程的三点线性边值问题

(1)

其中，ai,bi≥0(i=1,2)，a1+a2>0,b1+b2>0.

我们将讨论问题(1)、(2)的解的存在性与唯一性.

1 引理

下面考虑某一类二阶积分Volterra型微分方程的线性边值问题

(3)

(4)

引理1 如果方程(3)与边界条件(4)满足

(1)函数f(t,v,u)∈C([-1,1]×R2)，且在[-1,0]上关于v单调不减，在[0,1]上关于v单调不增;

(2)存在函数β(t)和α(t)∈C2[-1,1]，使得α(t)≤β(t)，

则边值问题(3)、(4)有解u(t)∈C2[-1,1]，使得α(t)≤u(t)≤β(t),-1≤t≤1.

(5)

它们满足以下不等式

(7)

又从条件(1)知，存在非负常数N1,N2，使得

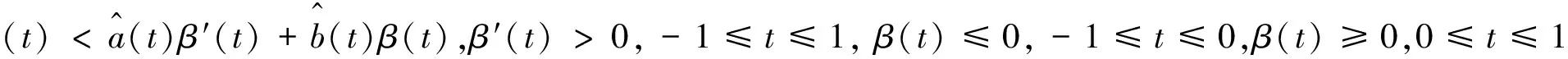
则边值问题

(8)

(9)

只有零解.

证明：利用反证法.

2 结论

最后我们将证明边值问题(1)、(2)解的存在性与唯一性定理.

定理1 如果方程(1)与边界条件(2)满足

(1)f(t,x,x′)∈C([-1,1]×R2)，且当-1≤t≤0时，关于x单调不减；当0≤t≤1时，关于x单调不增;

(2)存在函数α(t),β(t)∈C3[-1,1]，使当-1≤t≤1时α′(t)≤β′(t),α″(t)≤β″(t)，α‴(t)≥f(t,α(t),α′(t))，β‴(t)≤f(t,β(t),β′(t))，且当-1≤t≤0时，

则边值问题(1)、(2)有解x(t)∈C3[-1,1]，使得β(t)≤x(t)≤α(t),-1≤t≤0，α(t)≤x(t)≤β(t),0≤t≤1.

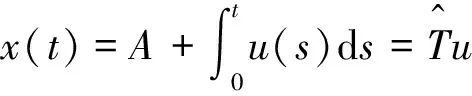
(1)′

(2)′

选取α′=α*,β′=β*，显然有α*≤β*，

此外，由条件(2)及f的单调性易知，当-1≤t≤1时

定理2 如果满足

(1)定理1中的条件(1)成立;

(2)存在函数β(t)∈C3[-1,1]，使当-1≤t≤1时0<β′(t),0<β″(t)，β‴(t)≤fx′(t,x,x′,x″)β′(t)+fx(t,x,x′,x″)β(t)，且当-1≤t≤0时，β(t)≤0，当0≤t≤1时，0≤β(t)，β(0)=0，0

证明：假设边值问题(1)、(2)有两个不同的解x1(t)，x2(t)，令y(t)=x2(t)-x1(t)，于是y(t)满足下述边值问题

定理3 如果满足

(1)函数f(t,x,x′)及其关于t,x,x′的一阶偏微商在闭区域Ω={(t,x,x′)|-1≤t≤1,-∞

(2)当(t,x,x′)∈Ω时，fx′(t,x,x′)≥m>0，当-1≤t≤0时，fx(t,x,x′)≥0，当0≤t≤1时，fx(t,x,x′)≤0，且|fx(t,x,x′)|≤l.

则边值问题(1)、(2)有且仅有唯一解.

证明：构造上下解分别为

其中，

M=max(M1,M2)，N=max(N1,N2).

余下的工作只需逐步验证β(t),α(t)满足定理1的条件即得存在性.

[1]王国灿.某一类三阶非线性两点边值问题的解的存在性与唯一性[J].应用数学学报， 1997，20(4):631- 634.

[2]WANG JINZHI.Existence of solution of nonlinear two point value problem for third order nonlinear differential equation[J].Northeasrn Math， 1991，7(2):181- 189.

[3]葛渭高.三阶常微分方程的两点边值问题[J].高校应用数学学报，1997，12(3):265- 271.

[4]沈建和，余赞平，周哲彦.非线性三阶常微分方程的非线性三点阶的存在性[J].纯粹数学与应用数学， 2007，23(3):355- 360.

[5]ZHAO WEILI.Singular Perturbations for Third order Nonlinear boundary Value Problems, onlinear Analysis[J].Theory,Methods and Applications，1994，44(10):1225- 1242.

[6]周钦德，苗树梅.Volterra 型积分微分方程的奇摄动[J].高校应用数学学报，1998，3(3):392- 400.

[7]王国灿.三阶非线性三点边值问题解的存在性和唯一性[J].大连交通大学学报，2012,33(3):86- 69.

[8]杜媛芳，王国灿.三阶微分方程三点边值问题奇摄动[J].大连交通大学学报，2009，30(4):108-110.

[9]BERNFELD S R,LASHMIKANTHAN V．An introduction to nonlinear boundary value problems[M].New York:Academic press，1974.

Nonlinear Third-Order Equation for Linear Three-Point Boundary Value Problem

WANG Guocan

(School of Mathematics and Physics, Dalian Jiaotong University,Dalian 116028,China)

In this paper, we study linear three-point boundary value problem for nonliear third order equation, by making use of upper and lower solutions method, existence and uniqueness of solutions are obtained.

nonlinear third order differential equation;linear three-point boundary value problem;existence and uniqueness;upper and lower solution

1673- 9590(2017)04- 0196- 03

2016- 12- 25

王国灿(1963-),男，教授,硕士，主要从事常微分方程的边值问题研究E-mail:wanggcshuxue@163.com.

A