修形对机车牵引齿轮动态特性影响

施晓春，刘东，单丽君

(大连交通大学 机械工程学院，辽宁 大连 116028)

修形对机车牵引齿轮动态特性影响

施晓春，刘东，单丽君

(大连交通大学 机械工程学院，辽宁 大连 116028)

以某机车牵引齿轮传动系统为研究对象，采用有限元方法模拟齿轮实际工况下的啮合状态，根据模型分析结果对齿轮进行修形，确定出齿轮修形的最佳修形量；计算修形前后齿轮系统的时变啮合刚度和接触线长度，计算结果表明二者都是呈周期性变化的，且正相关；建立了齿轮系统动力学数学模型，对比分析了修形前后齿轮系统动态响应，修形后齿轮系统的振动明显降低，说明齿轮传动更平稳，修形效果良好.

齿轮修形；时变啮合刚度；动力学响应

0 引言

机车牵引齿轮是机车行走机构的核心部件，其性能直接影响到机车运行的稳定和安全性.随着高速铁路时代到来，机车牵引功率越来越大，牵引齿轮的转速和载荷也相应提高，齿轮系统工作时不仅面临着更加严重的振动和噪声，其工作寿命也受到威胁.为增强机车牵引齿轮传动的平稳性，可采用的方法是尽量提高齿轮制造和安装精度，但同时增加了齿轮的制造成本，并且受到当前制造设备和加工工艺的限制.为解决这一难题，还可对牵引齿轮进行全齿面修形.

本文以某机车牵引齿轮传动系统为研究对象，采用有限元的方法模拟齿轮实际工况下的啮合状态，根据轮齿间的接触应力和静变形分析结果，对牵引齿轮进行齿面修形，确定合适的修形量，并采用有限元方法，拟合修形前、后齿轮系统的时变啮合刚度，分析了修形前、后齿轮传动系统的动态响应，对比验证了修形后齿轮传动更佳的平稳性.

1 齿轮传动的修形

文中所采用机车牵引齿轮参数如下：主、从动轮齿数z1=16，z2=91，螺旋角β=7°，法向模数mn=9.48，压力角αn=22.5°，齿宽b=127 mm.模拟其启动工况进行分析，主动轮扭矩为15 800 N·m.

1.1 齿廓修形量的确定

一对齿轮副工作过程是单、双齿啮合区的交替过程，在二者过渡过程中出现载荷突变，会导致轮齿弹性变形增加，基节改变，造成啮入啮出冲击.要消除这种现象，并减小振动和噪声，主要的方法就是齿廓修形.

牵引齿轮长期处于满载状态，同时在高速重载条件下，为防止齿根处产生过大的弯曲应力，故此在大小齿轮的齿顶分别采用长修形，即由啮合起始点或啮合终点到单齿啮合区的起始点或终点.并根据接触分析结果，确定进入位置即小齿轮齿顶最大修形量为0.058 mm，退出位置即大齿轮齿顶修形量为0.06 mm[1].

齿轮在高速重载情况下工作，采用明川，哥川推荐的修形曲线:

(1)

式中，Δmax为最大修形量；L为修形长度；x为修形点在修形曲线上的位置；其余参数及含义同前.建立齿廓修形后三维有限元模型[2].

1.2 齿向修形量的确定

齿轮传动系统在载荷的作用下将会产生轮齿的弹性变形、剪切变形及齿面接触变形，导致载荷沿齿宽方向分布不均匀.齿向修形的目的就是减小变形对载荷分布的影响，改善齿轮的偏载情况.

本文在小齿轮上进行齿向修形，提取有限元接触分析结果，提取小齿轮轴线的变形曲线，以此为齿向修形依据，根据反变形原理，结合加工特点，将修形曲线设计成为近似的鼓形齿.

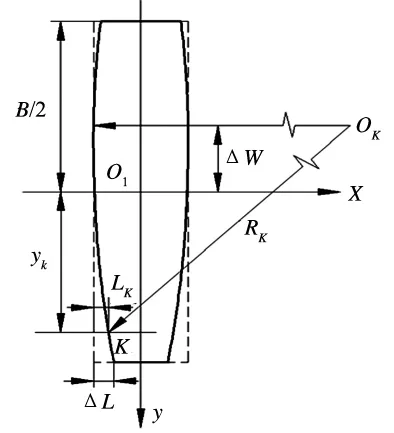
图1 齿向修形示意图

(2)

式中：K为待修形轮齿齿向方向任意一点.Rk为采用鼓形齿修形时的修形半径；ΔL为最大修形量，B为齿宽；ΔW为鼓形偏心距；Lk为任意点沿啮合线方向的修形量；见图1.由接触分析结果可知，设计拟合鼓形齿半径74 000 mm，最大鼓形量为0.112 1 mm，由于小齿轮为悬臂布置，为取得更好的修形效果，故鼓形齿中心位置远离电机端，其偏心距ΔW由计算得到21.7 mm.

1.3 全齿修形有限元模型

单一的齿廓修形或是齿向修形无法满足高速、重载机车牵引齿轮的性能要求，需要对轮齿进行全齿修形.建立全齿修形前后的有限元模型，如图2所示.可以看出，修形后齿轮在端面出现明显间隙，二者不再直接接触.

图2 全齿修形前后对比图

对修形前后齿轮系统有限元模型加约束载荷分析[3- 4]，主动轮接触应力分析结果如图3.

图3 修形前后主动轮接触应力云图

修形后主动轮的接触应力由512 MPa降低到455 MPa，并且原偏向于电机方向的偏载消失，齿向载荷分布更均匀，最大载荷位置出现在轮齿中心，向轮齿两侧依次减小，修形效果较好.

2 修形前后的时变啮合刚度计算

由于齿轮重合度一般不是整数，齿轮啮合过程中，同时参与啮合的齿对数随时间作周期性变化，每对参与啮合的轮齿产生的弹性变形也作周期性变化，此外，轮齿在从齿顶到齿根的啮合过程中，弹性变形也不相同，从而引起轮齿啮合刚度随时间作周期性变化，整个齿轮系统成为一个非线性时变刚度系统.

2.1 接触线总长度计算

在斜齿轮啮合过程中，随着齿轮的转动，实际处于啮合状态的接触线总长度随着时间变化而变化.实际接触线越长，载荷能更均匀的分布在齿面上，轮齿由于载荷所产生的变形更小，此时轮齿的啮合刚度更大.因此，计算斜齿轮任意时刻的接触线总长度对分析齿轮时变啮合刚度意义重大.

图4 斜齿轮啮合过程端面示意图

以端面重合度为标准， 齿轮啮合过程如图4所示，N1N2表示理论啮合线段，AD为实际啮合线线段，即一对轮齿从开始进入啮合到退出啮合全过程；齿轮在BC段工作过程中只有N对轮齿啮合，即为N齿啮合区，与之相对的AB和CD两段过程则中有N+1对轮齿啮合，为N+1齿啮合区(N为齿轮副总重合度数值εγ的整数部分).本文中，由于螺旋角数值较小，齿轮副总重合度系数值εγ<2，故啮合分为单齿啮合区和双齿啮合区.

在空间展开后，啮合线段AD则表示一对齿轮的啮合平面，如图5中ADEF所示，以Ln，Ln+1，Ln+2，Ln+3代表不同位置的接触线.在齿轮传动过程中，啮合平面保持不动，接触线向下(或向上)移动，处于啮合平面内的接触线(图中实线部分) 表示实际啮合状态.可推得，在一个啮合周期内，接触线总长度L的计算公式为：

(3)

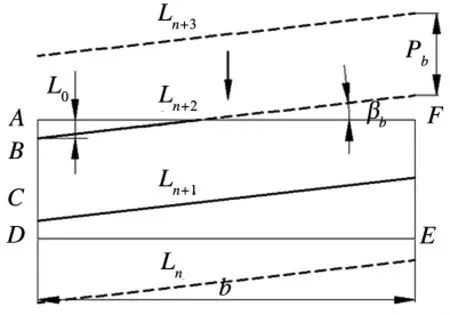
图5 接触线长度计算示意图

由式(3)计算得到的接触线总长度在图6中给出.

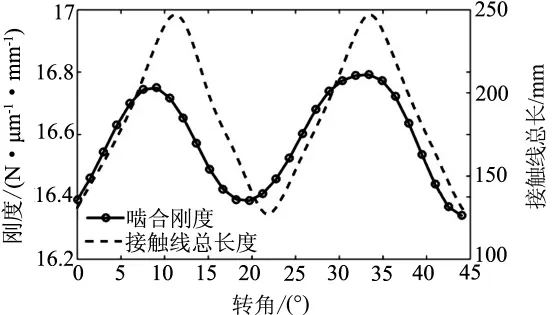
图6 啮合刚度与接触线总长度

2.2 时变啮合刚度计算结果

基于修形前、后机车牵引齿轮有限元模型，在一个啮合周期内不同转角下分别加载求解后，得到齿轮在一个啮合周期内不同转角下轮齿的变形量，根据轮齿刚度计算式(4)计算一个啮合周期内不同转角下啮合刚度[5].

(4)

式中：Fn是作用于齿廓的法向力；T是主动轮转矩；rb是基圆半径；B是接触齿宽；δ是轮齿沿啮合线变形.

根据有限元模型求得的变形量，并带入齿轮各参数，可拟合出啮合刚度kn的变化曲线，如图7所示[6].可以看出，修形后轮齿啮合刚度波动变得更加平缓，幅值也略有降低.

图7 修形前后齿轮啮合刚度

由图6可以看出接触线长度与齿轮的啮合刚度都是呈周期性变化的，没有突变，二者是正相关的.

根据齿轮时变啮合刚度曲线，拟合出时变啮合刚度计算表达式为[7]：

(5)

式中,km为平均啮合刚度；ω0=2πz1/T为齿轮啮合频率；an，bn为傅立叶级数展开系数，n=1,2,…,N.由于图6所得刚度曲线波形接近正弦函数，因此只需取一阶分量进行计算即可.

3 齿轮系统动力学模型的建立

3.1 物理模型

以已知某型号机车牵引齿轮的参数为例建立了齿轮系统的弯-扭-轴耦合振动分析模型.机车牵引齿轮副的动力学振动分析模型如图8所示[8].

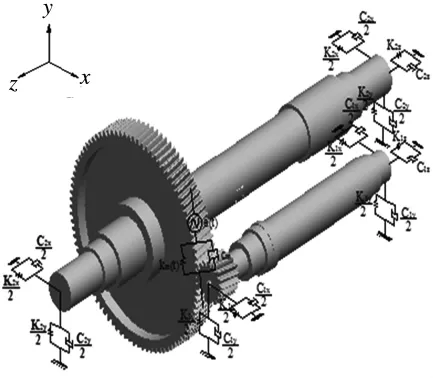
图8 斜齿轮系统动力学分析模型

在图8所示的分析模型中，各自由度方向的运动规律如下：

弯曲振动：由x，y方向自由度描述；

扭转振动：由θz方向自由度描述；

轴向振动：由z方向自由度描述.

3.2 数学模型

系统的广义位移矩阵{δ}可表示为

(6)

式中，xi,yi,zi,θiz(i=1,2)分别为主、从动轮中心点O1,O2在x,y,z方向的平移振动位移和转角振动位移.

模型建立不考虑轮齿间的齿面摩擦，根据建立的动力学模型推导出推导出系统的振动微分方程为:

(7)

式中：Mi(i=1,2)为主、从动齿轮质量；Iij(i=1,2;j=y,z)为主、从动齿轮转动惯量；cij(i=1,2;j=x,y,z)为主、从动齿轮两端支承阻尼；kij(i=1,2;j=x,y,z)为主、从动齿轮两端支撑刚度；T1，T2齿轮副驱动转矩和负载转矩[9].

模型中质量和转动惯量由齿轮系统参数计算得到，齿轮系统啮合刚度由式(5)计算，齿轮轴的轴向和弯曲刚度基于有限元模型计算得出，齿轮轴的扭转振动阻尼和齿轮的啮合阻尼按照经验公式计算[10].

4 修形前后齿轮系统响应分析

齿轮修形前后齿轮系统主要的参数变化体现在时变啮合刚度上，为研究修形对齿轮系统动态特性的影响，以Matlab软件作为开发工具，采用定步长Runge-Kutta数值方法对其振动微分方程进行求解，得到系统各自由度稳态响应.限于篇幅，仅给出启动工况下，修形前后主、从动齿轮系统垂直方向的时间历程图、相平面图、poincare截面及频谱图对比图，其余不再一一列出，如图9～10所示.

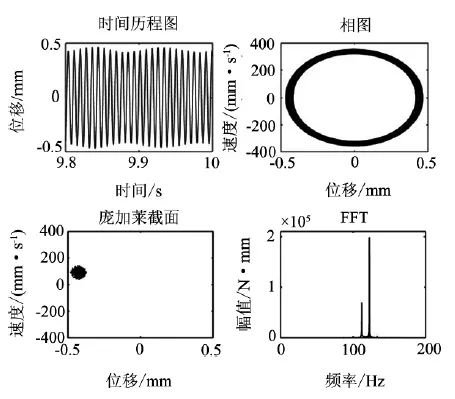
图9 未修形主动轮垂直方向仿真结果

图10 修形后主动轮垂直方向仿真结果

由垂直方向的仿真结果可以看出，该方向的振动幅值在没有修形时可达到0.48 mm，垂直方向的振动剧烈，这是由于垂直方向除了有啮合力外还有齿轮和车轴的重力，并且整个车体的质量均加载在该方向.且启动工况下，系统啮合频率为122 Hz，与该系统固有频率112 Hz非常接近，故此时系统振动非常激烈，幅值可达到其他工况的3倍以上，故取该时刻的运动进行分析颇具代表性.

而修形后主动轮垂直方向的仿真结果可以看出，振动幅值由0.48 mm降低到0.35 mm左右；振动更加平缓一些.由相图和庞加莱图可看出，修形后主动轮的振动速度及范围明显下降，且运动更加集中，运动规律更加明显.频谱图则显示出，系统的振动能量同时下降.修形有效的降低了齿轮系统振动.

5 结论

(1)根据齿轮系统有限元接触分析计算结果，确定了最佳修形量，小齿轮齿顶最大修形量为0.058 mm，大齿轮齿顶修形量为0.06 mm，齿向修形最大鼓形量为0.112 1 mm.根据修形量对有限元模型进行全齿面修形；

(2)采用有限元方法，计算了一个啮合周期内修形前、后齿轮系统时变啮合刚度，结果表明修形后时变啮合刚度幅值降低，刚度波动减小、没有明显突变，任意时刻啮合刚度与接触线总长度正相关，接触线越长，啮合刚度越大；

(3)齿轮系统在水平和垂直方向的振动幅值处于同一量级，但由于垂直方向负载较重，成为齿轮系统的主要振动来源.其振动幅值和速度均高于其他方向，频谱分析也显示该方向对应频率为122Hz，为齿轮啮合频率，即为系统振动主要因素；

(4)修形后齿轮系统的振动幅值、振动速度、振动能量均明显下降，齿轮传动平稳，进一步证明所确定的修形量是最优的.

[1]吴勇军,王建军,韩勤锴,等. 基于接触有限元分析的斜齿轮齿廓修形与实验[J]. 航空动力学报, 2011(2):409- 415.

[2]郑建辉，施晓春，何卫东. 基于APDL 的机车牵引齿轮齿廓修形分析 [J].大连交通大学学报，2015,36(6):15-19.

[3]鲍君华,何卫东,李力行.高速机车牵引齿轮的参数化实体建模及其动力学分析[J]. 机械传动, 2009, 33(5): 70-75.

[4]何卫东,王莹吉,鲍君华.电力机车传动系统支撑结构有限元分析[J].大连交通大学学报,2011,32(5):42- 46.

[5]陈思雨,唐进元,王志伟,等. 修形对齿轮系统动力学特性的影响规律 [J]. 机械工程学报，2014,50(13):59- 64.

[6]卜忠红,刘更,吴立言.斜齿轮啮合刚度变化规律研究.[J] 振动与冲击,2010,25(4):957-962.

[7]KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system [J]. Journal of Sound and Vibration, 1991, 146(1)：135-156.

[8]李润方,王建军. 齿轮系统动力学—振动、冲击、噪声 [M]. 北京:科学出版社,1997.

[9]UMEZAWA K. Vibration of power transmission helical gear with narrow face width[J].ASME Paper, 1984, 84：159.

[10]魏静，孙清朝，孙伟，秦大同，朱才朝，朱万刚，郭爱贵. 高速机车牵引齿轮传动系统动态特性及非线性因素影响研究 [J]. 振动与冲击,2012,31(17):38- 43.

Effect of Modification on Dynamic Characteristics of Locomotive Gear System

SHI Xiaochun, LIU Dong, SHAN Lijun

(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028,China)

Taking a locomotive traction gear transmission system as the research object, finite element method is used to simulate the meshing state of gear under actual working conditions. By modifying the tooth profile according to the results of contact model analysis, the optimal amount of modification is determined. Then, the time-varying meshing stiffness of the gear system and length of contact line are calculated before and after modification. The calculation results show that there are periodic and positive correlation. The dynamic mathematical model of gear system is established, the dynamic meshing performance of the gear system is compared before and after modification, and the vibration of gear system is greafly reduced. It shows that the gear transmission is more stable with good modification effect.

gear modification; time-varying mesh stiffness; dynamic response

1673- 9590(2017)04- 0110- 06

2016-03-16

辽宁省重大装备制造协同中心资助项目

施晓春(1974-)，女，副教授，硕士，主要从事机械设计及理论的研究E- mail:shilikang@sina.com.

A