城市公交车辆有限状态的到站时间预测

王茁,程绍武

(1.大连科技学院 交通运输学院，辽宁 大连 116052； 2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 154100)

城市公交车辆有限状态的到站时间预测

王茁1,程绍武2

(1.大连科技学院 交通运输学院，辽宁 大连 116052； 2.哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 154100)

在分析影响公交车辆到站时间影响因素的基础上，选取模型的输入变量和输出变量，设计基于城市公交车有限运行状态的自动机模型，通过对不同时段的到站时间预测模型分析，提出了一种复合的公交车辆到站时间预测模型，并通过实例分析证明有限状态自动机预测模型较单一预测模型预测结果更为精准，对于城市公交车辆到站时间预测工作具有一定的现实意义.

城市公交；公交车辆；有限状态；自动机；到站时间

0 引言

对选择公共交通方式的出行者来说，公交车辆到站时间可以说是出行者最关心的公共交通出行信息，提高预测公交车辆到站时间的精准度，改善公交出行可靠性，提高公交出行分担率，也是有效缓解城市交通拥堵，打造低碳高效的城市交通的重要手段.本文分析影响公交车到站时间的影响因素分析，划分公交车辆运行的有限状态，提出有限状态自动机模型，设计到站时间预测模型，提高公交车辆到站时间预测工作的精度和可靠性，不仅能够提高公共交通对居民出行的分担，而且对城市的公共交通服务体系的向前发展也在一定程度上起了推动的作用.

1 公交车辆到站时间的影响因素

1.1 公交车辆到站时间影响因素分析

不同乘客对公交车辆到站时间的需求标准各不相同，分析影响公交车辆到站时间的因素及其构成，可以从根源上把握提高城市公共交通服务水平和公共交通服务可靠性的重要指标，从而提升公交车辆导致时间预测的准确性.总结影响公交车到站时间的各项可能构成要素，主要包括路段行驶时间、停靠延误时间和交通状态等三个方面：

(1)路段行驶时间影响因素

车辆在不受外界任何干扰并能以正常行驶速度行驶至整段里程结束，可能会对这个过程造成影响的这些因素被称作是影响路段正常行驶因素，它们可能是除车辆正常行驶过程中等候乘客上下车的停驻时间及道路交叉口等待时间之外的其他一切因素，总结来说有七个方面：道路因素、车辆因素、人的因素、交叉口因素、交通拥堵因素、季节天气因素及突发事件因素.

(2)停靠站延误时间影响因素

停靠站延误时间主要是指由于公交车辆进站离站、开关门、乘客上下车等在站点停靠过程中所消耗的时间之和，同时还受公交车辆本身的性能、候车站台长度、乘客上车购票方式、不同时间的上下车客流流量等因素的直接影响[1].

(3)交通状态影响因素

道路上的各种组成因素的状态每时每刻都是非常复杂的，运行在道路上的各种各样车辆的特性也不尽相同，如：车辆型号、目的地、行驶路线.同时，车辆随着行驶路线进入相应地段的路面环境等也会有不同程度的变化，此外，驾驶车辆的驾驶员本身特点也很难找出相似的变化规律.尽管如此，以上分析的各种情况交织在每日的路面，但仍然可以从中归纳出具有一定倾向的状态.道路交通运行状态可以用交通流特征来进行定性和定量的描述，相应的物理量称之为交通流参数.其主要包括的内容有交通流量、速度、道路交通密度、时间占有率和空间占有率、车辆排队长度、车头时距及车头间距[2].

基于上述分析，影响到站时间的人的因素和环境因素相互作用十分复杂，选取适当的影响因素将对公交车到站时间预测模型的预测结果有着直接的决定性作用，而且还要对选取的因素进行合理的量化，以提高预测的精度[3].各因素具体量化方法如表1所示.

表1 公交车辆到站时间影响要素分析

1.2 公交车辆到站时间影响因素的选取

针对我国城市复杂的交通状态，将各种影响道路行驶中车辆的延误因素用一个指标代替表达[4]，以达到量化导致公交延误的因素，公交线路l在d走向上的第k个站点的延误程度可表述为：

本文选取站点延误程度对其影响程度进行描述，同时利用停靠时间来表征公交车辆在公交站点内的特征.选取公交车辆到达当前所处站点的后续站点时间与到达前续站点时间的差值作为模型的输入变量，相应的预测得出的两个站点间运行时间作为输出变量，能够较全面地反映各项交通因素对公交车辆运行的影响.

2 公交车辆的有限状态自动机模型

2.1 公交车辆运行状态的有限状态自动机模型

在有限状态自动机原理的基础上，结合对公交车辆运行状态的划分，将公交车运行系统分为四个部分：Q={开始，预测，中间，未知}；定义∑为来自GPS定位的实时数据信息；q0是未知状态；F设定为预测的状态.到站系统的有限状态自动机的等价转换图如1所示.

图1 有限状态自动机到站时间预测系统的状态转换

在此基础上将城市公交运行状态，划分为四个阶段，并对各个状态给予条件设定[5]：

(1)开始状态.公交车辆运行在城市道路上，排除天气、时间段、节日游行等这些可能的影响因素，公交车辆能够以平均运行速度行驶在既定路线上的，此时应该是公交车车速均匀、每站都有相似的换乘人数、驾驶员的状态良好，此时称公交车辆的这种运行状态为开始状态;

(2)预测状态.规定一个公交车在运行当中所处有限多个的预测状态，检测处于此状态中时，对公交车的到站时间进行预测.按时间段将预测状态划分为以下三个阶段：高峰时段的预测状态、平峰时段的预测状态、低峰时段的预测状态;

(3)中间状态.公交车在实际运行的过程中到达某一调度点或到达某一个时间段，有可能出现：连续几站无人上、下车，这时公交司机会选择做出中间不停车的处理；或是车辆正常行驶在既定路线上出现了缺油而决定临时加油；路面突发状况进行抢修等，将此状态定义为中间状态;

(4)未知状态.公交车辆运行中的一个最不能够忽视的是在运行过程中可能会遇到的一些无法识别的异常状态，比如GPS无信号，实时的相关数据无法获得.为保证此时的预测系统能够继续工作，为保证其能在任何时间正常运转为乘客提供可查信息，设置一个未知状态.

2.2 公交车辆运行状态转移

(1)开始状态.由车载设备实时获得的GPS数据，得知每个公交车辆任一个时刻的速度，乘车人数、驾驶员信息等和当前车辆在运行路线上的位置信息，判断公交车辆的既定路线和上下行驶向正常与否.若开始观测状态为正常则进入设计系统的预测状态，δ(开始，开始正常)=预测状态；若不正常的开始状态，则有δ(开始，开始异常)=未知状态;

(2)预测状态.公交车辆正处于正常状态运行是进入预测状态的前提，本文假定预测状态调用有限状态自动机预测模型对公交车在两个站间的运行时间进行预测，相反地，若出现GPS数据异常或残缺、有突发状况司机改线运行或某站未停车等现象，则进入未知状态处理;

(3)中间状态.公交车在实际运行当中到达某一调度点或到达某一时间段，有可能会有连续站无人下车无人上车而中间不停车、缺油临时加油、突发状况抢修等情况发生，若检测到公交车辆满足此状态，规定δ(中间状态)=未知状态，此时在该状态下启用时间序列预测模型;

(4)未知状态.在运行中遇到一些无法识别的异常状况，公交车辆在此阶段的运行速度、乘车人数、驾驶员信息等和当前车辆在运行路线上的位置信息都无法获得时，认为系统处在未知状态，完成预测后会自动回到开始状态，以保证这个正常启动循环进行下去.

2.3 有限状态自动机状态自识别框架

采用人工巡逻、电话识别、电视识别以及自动电子监视识别等道路交通状态的识别方式，对比分析它们的使用条件，考虑道路交同状况对公交车运行状态的影响，运用当前一种基于公交车辆GPS历史数据的交通流运行状态自动识别方法，分析得到公交车辆运行状态判别方法与应用的基本框架如2所示.

图2 公交车辆运行状态判别方法与应用基本框架

3 不同时段的到站时间预测模型

针对本文的研究对象，对公交车运行中的预测状态的三个时段选取三种预测模型，分别对应平峰时段的Kalman滤波预测模型，高峰时段的BP人工网络预测模型，以及低峰时段的ARIMA时间序列预测模型.从而建立公交车辆有限状态自动机的预测模型构想，并结合有限状态自动机的设计原理，设计并建立本文的预测系统模型.

3.1 平峰时段的Kalman滤波预测模型

假设公交车辆在站点k运行到终点的时间为tk，车辆从站点k到k+1站的时间用Tk,k+1表示，出发点到k站的时间用Sk表示，从而可以得到k+1站到终点的运行时间可以用公式tk=tk+1-Tk,k+1计算求得tk+1，那么出发点到k+1站的时间即为Sk+1=Sk+Tk,k+1.

设从出发点到站点的运行时间观察值用Zk表示，即Zk=Sk.令Xk=(tk,sk)T，则该离散系统的状态方程和观测方程为：

Zk=HkXk+Vk

3.2 高峰时段的BP神经网络预测模型

本文的BP神经网络预测模型采用三层BP神经网络.隐含层节点数有2×5+1=11个，输出层为车辆运行到个车站的实际时间有1个节点，于是可以确定BP神经网络的设计结构为5×11×1，如图3所示.基于BP神经网络构建的公交车到站时间的预测模型如下图4所示.

图3 BP网络结构

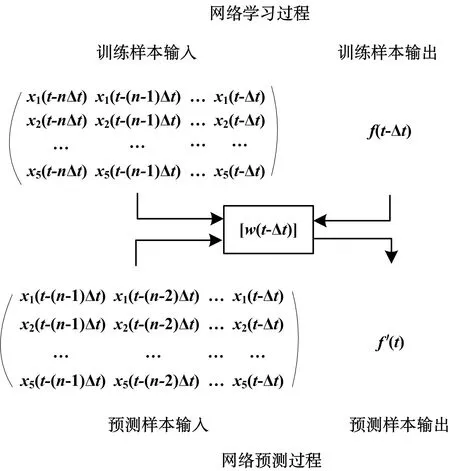
图4 BP神经网络预测模型的学习与训练

其中,x1为车辆在t时刻到终点的距离;x2为天气情况;x3为星期因素;x4是节日因素;x5获得GPS传输数据的那一时刻.

t时刻神经网络的学习过程可以这样表述为：输入为xi(t)，样本输出为(t-Δt)时刻的到达时间，然后对网络进行训练得到该时刻的神经网络权重的对应矩阵.而在该时刻的预测过程则为：与学习过程相同，样本输入为xi(t)不变，用训练好的网络进行预测.

3.3 低峰时段的ARIMA时间序列预测模型

对于非平稳的时间序列，用若干次差分使其成为平稳序列，再用ARIMA(p,d,q)模型对该平稳序列建模，之后经反变换得到原序列.=1-B表示差分算子，对非平稳序列{xi}进行d阶差分得到{dxi}是一个平稳序列，假设它适合ARMA(p,q)模型，其中φ(B)=1-φ1B-…-φpBp,θ(B)=1-θ1B-…-θqBq，则ARIMA(p,d,q)模型结构如下[6- 7]：

其中，p，d,q分别表示自回归阶数，差分阶数和移动平均阶数，故称为求和自回归滑动平均模型.显然当d=0时，ARIMA(p,d,q)模型就是ARMA(p,q)模型，可见ARIMA(p,d,q)模型和ARMA(p,q)模型的主要区别就在于d是否等于0，即序列是否平稳，前者是非平稳模型，后者是平稳模型.在用ARIMA(p,d,q)模型时就是对非平稳序列进行d阶差分，然后对差分后的序列判断平稳性，当差分后的序列平稳时，再对其建立ARMA(p,q)模型[7].建模流程图如图5.

图5 时间序列建模流程

4 实例分析

以某城市GPRS无线通信网络接收车辆传输而来的某线路公交车辆三周的公交数据，考虑到本文提出的有限状态自动机预测模型所选用的三种模型适用条件的不同，将处理得到的两个礼拜的工作日(即10天)的运营时间5∶00∶00～22∶00∶00分为三个时段，分别提取所需时段的数据进行实验，具体划分及提取原则如表2所示.

运用三种预测方法对公交车运行一天划分的三个时段，分别进行到站时间预测实验的结果可以得到，由于ARIMA时间序列模型不适用于本文的对公交车辆运行中对到站时间的预测，因此，公交车辆运行的预测状态仅选用Kalman滤波模型和BP人工神经网络模型.

表2 某城市预测状态下的时间段具体划分

Kalman滤波的公交车到站时间预测模型在公交车运行中预测状态下的预测误差，通过MATLAB2012a实现，统计结果如图6所示.

(a)高峰时段

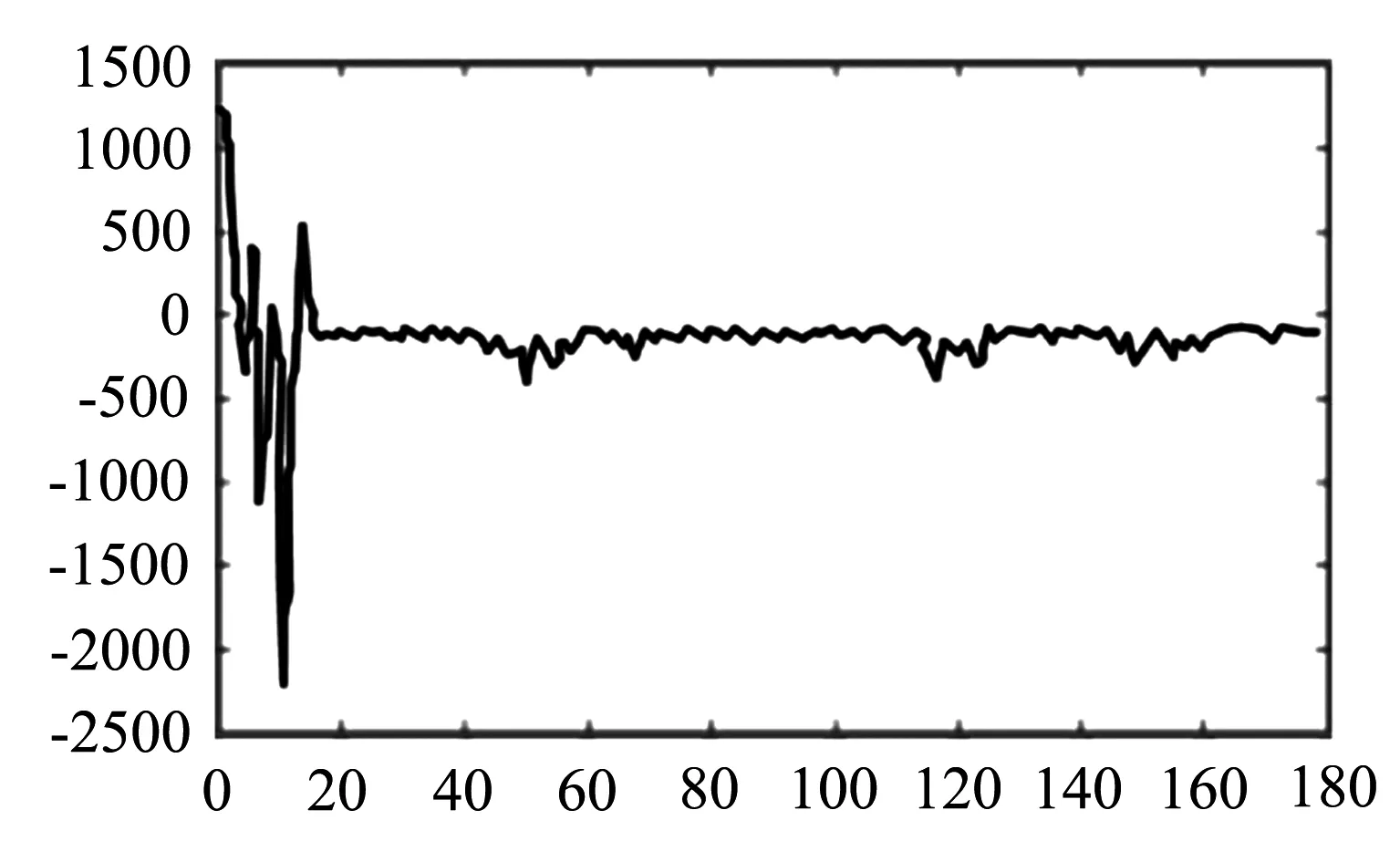
(b)平峰时段

(c)低峰时段

同样的，BP人工神经网络的公交车到站时间预测模型在各个运行时段的预测误差统计结果如图7所示.

(a)高峰时段

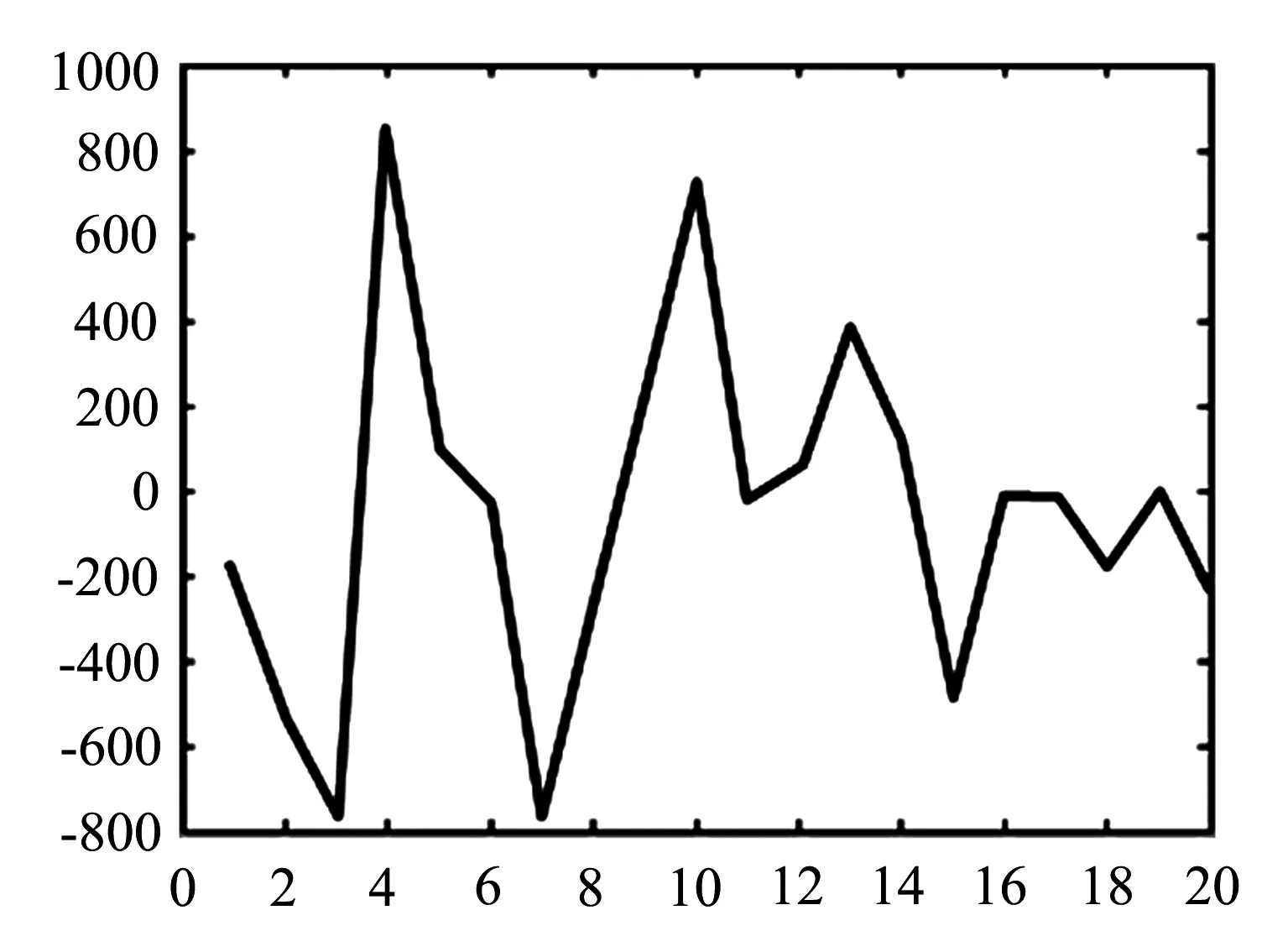
(b)平峰时段

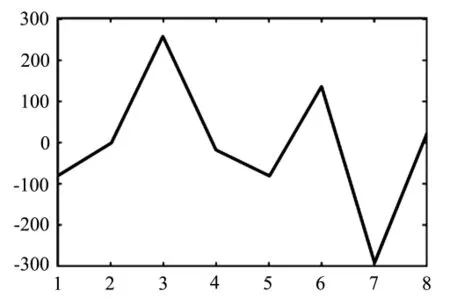
(c)低峰时段

再对高峰时段和低峰时段采用BP人工神经网络预测模型，平峰时段采用Kalman滤波预测模型，对已知数据)进行有限状态自动机预测模型的实验仿真模拟，通过MATLAB2012a实现，得到的绝对平均百分误差如表3所示.

表3 两种预测模型的绝对平均百分误差统计

统计一日该路公交全天的实测数据共440个，其中高峰时段175个，平峰时段182个，低峰时段83个，按照表中两种预测模型的MAPE值和各个时段的数据占总数据的比例，可以计算求得预测模型的相对MAPE值，即：Kalman滤波预测模型15.4%、BP神经网络预测模型11.87%、有限状态自动机预测模型8.56%.

进一步求得有限状态自动机的预测模型相对两种单一预测模型的精度分别提高的百分比为44.42%和27.89%.

5 结论

从城市交通中公交车辆运行状态划分的角度出发，提出并建立公交运行状态的有限状态自动机模型，经过实例分析仿真模拟，证明应用复合的有限状态自动机预测模型预测精度确实较单一预测模型有很大提高.在一定程度上提高了预测的精准度，由此证明本文提出的模型确有应用于公交车辆到站时间预测工作的现实意义．

[1]AVISHAI CEDER.公共交通规划与运营：理论、建模及应用[M].北京：清华大学出版社，2010：89- 124.

[2]李江.交通工程学[M].北京：人民交通出版社，2002.

[3]田林，韩存玉.对城市交通拥挤问题的分析[J].黑龙江交通科技,2006(6)：125- 130.

[4]周干峙.发展我国大城市交通的研究[M].北京：中国建筑工业出版社，1997：57- 62.

[5]周涛.基于有限状态自动机的复合事件检测的程序实现[M].计算机工程，2005，31(23)：85- 86.

[6]KOSKO BART.Neural networks and fuzzy systems：A dynamical approach to machine intelligence[M].Englewood Cliffs：Prentice Hall,1992：76- 89.

[7]艾玲.时间序列短期预测的方法和技术[D].上海：华东师范大学，2010.

City Bus Arrival Time Prediction of Finite State

WANG Zhuo1,CHENG Shaowu2

(1.Faculty of Transportation Engineering,Dalian Institute of Science and Technology,Dalian 116052,China; 2.School of Traffic Science and Engineering,Harbin Institute of Technology,Harbin 154100,China)

On the basis of analyzing the factors influencing the bus arrival time,input variables and output variables of the model are selected,and the model of automaton is designed based on bus limited running status.By analyzing the arrival time at different times of the prediction model,a composite of bus arrival time prediction model is proposed.Through the instance analysis,the predicted results show that the finite state automata model is more accurate than a single forecasting model,which indicates the model for city bus arrival time prediction work has a certain practical significance.

public transportation;bus;limited traffic state;automata;bus arrival time

1673- 9590(2017)04- 0001- 06

2016- 08- 15

王茁(1987-)，女，工程师，硕士，主要从事城市交通规划及铁路运输方面的研究E-mail:ichigo_715@163.com.

A