金红石TiO2本征缺陷磁性的第一性原理计算∗

林俏露李公平†许楠楠刘欢王苍龙

1)(兰州大学核科学与技术学院,兰州 730000)2)(中国科学院近代物理研究所,兰州 730000)(2016年9月2日收到;2016年10月12日收到修改稿)

金红石TiO2本征缺陷磁性的第一性原理计算∗

林俏露1)李公平1)†许楠楠1)刘欢1)王苍龙2)

1)(兰州大学核科学与技术学院,兰州 730000)2)(中国科学院近代物理研究所,兰州 730000)(2016年9月2日收到;2016年10月12日收到修改稿)

基于密度泛函理论的平面波超软赝势方法模拟计算了金红石相TiO2的四种本征缺陷(氧空位、钛空位、钛间隙缺陷、氧间隙缺陷)和两种复合缺陷(氧空位与氧间隙复合缺陷、钛空位与钛间隙复合缺陷)的铁磁特性.结合态密度、电子分布及晶体结构变化分析可知,四种本征缺陷均会在系统内引入缺陷态.氧空位、钛间隙缺陷使费米面升高,引起自旋极化,引入磁矩分别为1.62µB与3.91µB;钛空位的缺陷态处于价带顶,使费米面进入价带,表现出明显的p型半导体特性,引入磁矩约为2.47µB;氧间隙缺陷引入缺陷态但仍然处于自旋对称状态,费米面略微下降;氧空位与氧间隙复合缺陷使费米面上升的程度比单个氧空位时大,模拟的超晶胞保持了氧空位的铁磁特性,大小为1.63µB;钛空位与钛间隙复合缺陷以反铁磁方式耦合,但超晶胞仍具有一定的铁磁特性.

第一性原理,本征缺陷,态密度,自旋磁矩

1 引 言

随着信息技术的发展,以Si基半导体为代表的电子器件发展正在逐渐逼近理论极限,同时具有电子电荷和自旋属性的自旋电子学器件为这一问题的解决指明了新的发展方向.稀磁半导体(diluted magnetic semiconductor,DMS)作为可同时兼顾两种属性的半导体材料而成为研究的热点.然而受居里温度过低等因素的影响,DMS材料目前尚不具备应用基础.2000年,Dietl等[1]基于平均场理论建立了Zener模型,并以此为基础预言Mn掺杂的p型ZnO和GaN可以在室温下产生铁磁性;2001年,Matsumoto等[2]在通过激光束外延技术制备的Co掺杂TiO2薄膜上测量到高居里温度(400 K)的铁磁特性,间接证明了Dietl等[1]的预言.实验上,在Sc,V,Cr,Mn,Gd等掺杂TiO2[3−13]体系中均测量到了室温铁磁性.对于部分掺杂TiO2系统,有报道认为样品的磁性源自掺杂磁性离子形成的磁性第二相[8,9]或内部载流子的调控作用[10],更有文献认为磁性是由TiO2自身的点缺陷引起的[11−13],通过掺杂形成的本征缺陷是决定磁性产生的主要因素,因为通过常规超交换或双交换相互作用,过渡金属阳离子的替位浓度不足以让样品产生长程磁序,因此磁性也可能起源于TiO2衬底自身的氧空位或其他本征缺陷.

第一性原理计算允许模拟单一因素对样品物理性质的影响,因而成为理论研究TiO2本征缺陷的主要手段.Stausholm-Møller等[14]基于密度泛函理论讨论了不同取值的Hubbard-U近似时Ti间隙原子对TiO2态密度与自旋极化状态的影响,间接证明了Ti间隙原子对TiO2铁磁性有一定贡献.Shi和Wang[15]采用局域密度近似的方法计算了金红石相TiO2多种本征缺陷的磁性,认为氧空位和钛空位缺陷的存在将引入磁性,磁矩大小与缺陷提供的自由电荷数目相同,但是Zarhri等[16]采用相同的计算方法却得出氧空位、钛空位、氧间隙和钛间隙本征缺陷均不会引起自旋极化现象的结论.Kim等[17]采用全势能线性缀加平面波计算了金红石相TiO2氧空位引入的铁磁特性,指出与氧空位相临近的Ti原子的平均磁矩为0.22µB.不同于Kim等[17]的计算结果,Máca等[18]与Yang等[19]通过局域密度近似与广义梯度近似方法计算了TiO2氧空位对样品铁磁性的贡献,结果表明金红石相TiO2的氧空位并不会引入磁性,磁性仅与阳离子空位有关.关于本征点缺陷是否能引入磁性仍存在争议,且相同浓度缺陷引入磁矩差异较大,对于引入磁性缺陷铁磁的耦合方式及居里温度的探讨较少,并未考虑布居数与缺陷的关系,对磁性来源机理不明,涉及复合缺陷磁性的计算更少.因此,本文以本征缺陷和简单复合缺陷为依托,使用第一性原理方法分别计算了不同缺陷类型的磁学性质,并从几何结构、态密度和布居数变化等方面分析了铁磁性的形成机理,并评估了其居里温度.

金红石相TiO2因具有较好的热稳定性而具有更广阔的使用前景,其本征点缺陷主要包括钛空位、氧空位、钛间隙、氧间隙和反位缺陷.通过对缺陷形成能[20]的计算可知,所有本征缺陷中氧空位形成能最小,且氧空位可通过mTiO2+2n VO2+→(m−n)TiO2+n Ti4++2n e−反应转化为钛间隙缺陷[21],其中表示氧空位,e−表示电子,m与n表示个数.富钛条件下,钛间隙缺陷的形成能比较低.富氧条件下,则比较利于钛空位和氧间隙的形成[15,22],但任何条件下反位缺陷的形成能远高于其他缺陷的形成能[23],使得缺陷浓度非常低.因此本文以金红石相TiO2的氧空位、钛空位、钛间隙、氧间隙本征缺陷、氧空位与氧间隙复合缺陷、钛空位与钛间隙复合缺陷为研究对象,探索TiO2样品本征缺陷对TiO2基DMS室温磁性的影响.

2 计算方法与计算模型

2.1 计算方法

计算基于密度泛函理论的平面波超软赝势,交换关联泛函采用广义梯度近似 (generalized gradient approximation,GGA)中的Perdew-Burke-Ernzerhof泛函,自洽精度为每个原子能量收敛到0.1455×10−6eV,平面波截止能量为340 eV,第一布里渊区的k点网格设置为3×3×4.为满足计算要求,采用的超原胞大小为2×2×2(Ti16O32).由于密度泛函理论计算中过渡金属原子中d轨道电子的轨道占据以及自旋相关的关联能不能被忽略,且氧原子p轨道电子的关联性微扰项量级与d轨道的相当,因此本文计算采用GGA+U方式,综合前人的工作[15,24],Ti的d轨道和O的p轨道微扰项U的取值分别为Ud=5.7 eV,Up=4.3 eV.

2.2 计算模型

金红石的每个钛原子位于六个氧原子形成的一个八面体的中心,该八面体极点位置的Ti—O键长为1.974Å,赤道位置的Ti—O键长为1.953Å,赤道面的边长分别为2.959Å,2.536Å,完美晶胞结构如图1所示.金红石TiO2为四方晶系,空间群为,晶格常数为a=b=4.594Å,c=2.959Å[25,26],禁带宽度为3.02 eV,带隙类型为直接带隙.

计算的缺陷类型中氧空位(VO)和钛空位(VTi)通过移去TiO2晶格中特定位置的O原子和Ti原子获得;钛间隙(Tiin)和氧间隙(Oin)则是在TiO2晶格中六个钛原子组成八面体中心位置上放置中性Ti原子和O原子来产生;氧空位与氧间隙复合缺陷(Ocom)、钛空位与钛间隙复合缺陷(Ticom)则通过同时放置与移除原子获得.

图1 (网刊彩色)完美晶胞结构图Fig.1.(color on line)Schematic d iagramof the perfect structu re cell.

3 计算结果与讨论

由结构弛豫后晶胞参数的变化(见表1)可知,VO,VTi,Ocom和Ticom的引入导致晶格膨胀.Tiin,Oin原子到达平衡态前处于中性状态,因缺少静电吸引也会使晶格膨胀,与Santara等[27]报道的结果一致.

表1 完美晶胞与四种缺陷晶胞弛豫后的结构参数Tab le 1.Structural parameters of the perfect and the lattice with defect(s)after the structure relaxation.

图2 (网刊彩色)完美晶胞(a)O原子分态密度(PDOS),(b)Ti原子分态密度,(c)总态密度(DOS)以及(d)能带结构图Fig.2.(color on line)The partial density of states of(a)Oand(b)Ti,(c)the total density of states and(d)band structure of the perfect structure.

图2(c)为完美金红石TiO2态密度分布图,0 eV处为费米能级.通过GGA+U的修正,完美晶胞金红石TiO2的带隙约为3.01 eV,与实验值一致,也与其他文献[24,28,29]的报道契合.导带主要由Ti原子的3d轨道电子构成,价带的组成则主要来自O的2p轨道,价带底距离费米面约−6.0 eV.密度态中多数自旋与少数自旋明显对称,无自旋极化现象,因此无缺陷的金红石TiO2为非铁磁性材料.

3.1 VO,VTi,Tiin和Oin本征缺陷

单个VO缺陷晶胞自旋极化体系的总能量比非自旋极化体系的总能量低约200 meV.VO的引入使周围的三个钛原子因库仑力而向外推,最大移动距离约为0.3Å,但邻近的氧原子却被向内吸引了大约0.1Å.由电荷布居数可知,因氧空位的引入使得氧空位周围的O原子的电负性增加,结构图3中(1)号位置的O原子的电荷布居数由−0.72变为−0.76,其磁矩为0.19µB,而氧空位周围的Ti原子的正电性减弱,结构图3中(2)号位置Ti原子的电荷布居数变化最大,由1.45变为1.37,贡献的磁矩为0.82µB.

图4(c)为单个氧空位的金红石TiO2的总态密度图.可知,VO使费米面上升,且在费米能级附近引入一个缺陷态,该缺陷态的位置在导带低约0.7—1.0 eV处,与Lee等[30]的计算结果相似.

图3 (网刊彩色)弛豫后氧空位缺陷(VO)晶胞结构图Fig.3.(color on line)Schematic diagrams of the structu re with one oxygen vacancy defect after the relaxation.

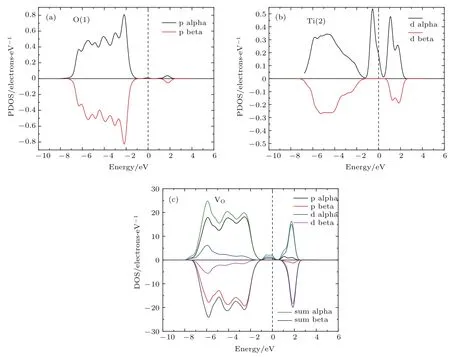
图4 (网刊彩色)局域原子(a)O(1),(b)Ti(2)分态密度图和(c)含VO缺陷晶胞总态密度Fig.4.(color online)The partial density of states of(a)O(1)and(b)Ti(2),and(c)the total density of states of the crystal cell with one oxygen vacancy.

模拟中引入的缺陷位置与实验上通过紫外光电子能谱分析法(ultraviolet photoelectron spectroscopy,UPS)和电子能量损失谱分析(electron energy loss spectroscopy,EELS)测量到的晶体氧空位引入的缺陷态位置一致[31,32].这个缺陷态使上下自旋不再对称,体系处于自旋极化状态.此缺陷态是由氧空位引入的两个局域电子导致.模拟的电子自旋密度分布(本文未给出)显示,其中一个电子将占据相邻的Ti原子的3d轨道,与实验上电子顺磁共振测量到的被还原钛原子的价态和位置结果相符[33].由图4(b)可以看出,缺陷态主要由Ti 3d贡献,另一个电子可能被禁锢在空位中形成F色心[34],这个电子所占据的轨道与相邻O原子的2p轨道重叠,因此缺陷态也有一小部分是杂化O2p轨道的贡献,如图4(a)所示.布居电荷数的变化也可以间接说明Ti 3d轨道伸向VO区域,与该区域电子发生杂化.而这个交换作用所获得的能量补偿大于电子局域化产生的能量损失时,根据Stoner判据[35](stoner criterion)可知,电子的能带将发生自旋分裂.引入VO后能带间隙中有缺陷态,由于原子内相互作用使得自旋向上的密度态穿过费米面,能带结构转化为半金属态,从而晶体表现出半金属铁磁性,晶胞总磁矩为1.62µB.本文计算的氧空位引入的缺陷并非紧贴导带底,费米面也未上升至导带底处,这是因为空位周围Ti原子电荷密度的分布伸向VO区域,电子局域性较强,此结果与Zhao等[36]的计算结果略有差异.

对于VTi缺陷,晶胞经过晶格弛豫后临近的钛原子向空位靠近了大约0.1Å,而氧原子则远离空位约0.2Å.由电荷布居数可知,引入VTi使得空位周围的O原子的电负性减小,结构图5中(1)与(2)号位置的O原子的电荷布居数由−0.72变为−0.60与−0.57,磁矩分别为0.1µB与0.34µB.而空位周围的Ti原子的正电性增强,结构图5中(3)号位置Ti原子的电荷布居数变化最大,由1.45变为1.52,Ti—O的共价键能力减弱,其贡献的磁矩为0.15µB.

图6(d)为具有一个VTi缺陷晶胞的总态密度图,价带仍然由O2p和Ti3d杂化组成,而导带由Ti 3d和弱杂化的O2p贡献.VTi引入后费米面附近的价带顶态密度处出现一个缺陷能级,费米面进入价带,晶体转变为p型半导体.完整TiO2晶体中Ti和O以近似sp2的方式杂化成键,价带由低到顶分别为σ键、π键和未成键O2pπ.VTi引入后两个O(2)的态密度图如图6(b)所示,态密度在赤道面的O原子上对称分布,使得结构图中两个O(2)与Ti(3)组成的平面三角形O—Ti—O具有明显的O2pπ特征.因此可认为Ti4+空位会在O2pπ窄带上形成空态,使低能量的自旋向上子带和高能量的自旋向上子带发生交换劈裂引起极化,也就表明VTi引入的磁性主要由空位周围氧原子的2p轨道贡献.VTi附近其他O,Ti原子的态密度的微小变化可认为是因电子的局域化导致的.由于占据自旋向上子带的电子数目较多,使得系统能量更低,极化引入的磁矩为2.47µB,与12.5%和25%的VTi缺陷产生的极化磁矩(分别为3.76µB与4.01µB)相比[37],这个数值偏低,主要与缺陷浓度相关[38,39].

对于包含一个Tiin的晶胞经过弛豫后赤道面的氧原子向间隙原子靠拢,间隔从2.206Å缩短到1.98Å,而其他位置的原子均远离钛间隙原子.由电荷布居数可知,引入Tiin使得间隙原子周围的O原子的电负性增加,结构图7中(4)号位置的O原子的电荷布居数由−0.72变为−0.77,结构图7中(1),(2),(3)号位置间隙原子周围的Ti原子的电荷布居数由1.45变为1.12,1.41,1.46,形成的磁矩分别为0.63µB,0.15µB,0.69µB.从图8(e)可知,Tiin原子引入两个缺陷能级,其中一个处于导带底约0.3 eV的位置,另一个处于带间中部靠近导带底约1.1 eV的位置.这与UPS或EELS测量到的单峰稍有区别[40],可能是实验测量峰的半高全宽较大,导致多个峰堆叠,也可能是浅杂质能级只适合在较低温度下观察,若实验温度稍高将很难观察到清晰的峰.

图5 (网刊彩色)弛豫后钛空位缺陷(VTi)晶胞结构图Fig.5.(color on line)Schematic d iagrams of the structure with one titaniumvacancy defect after the relaxation.

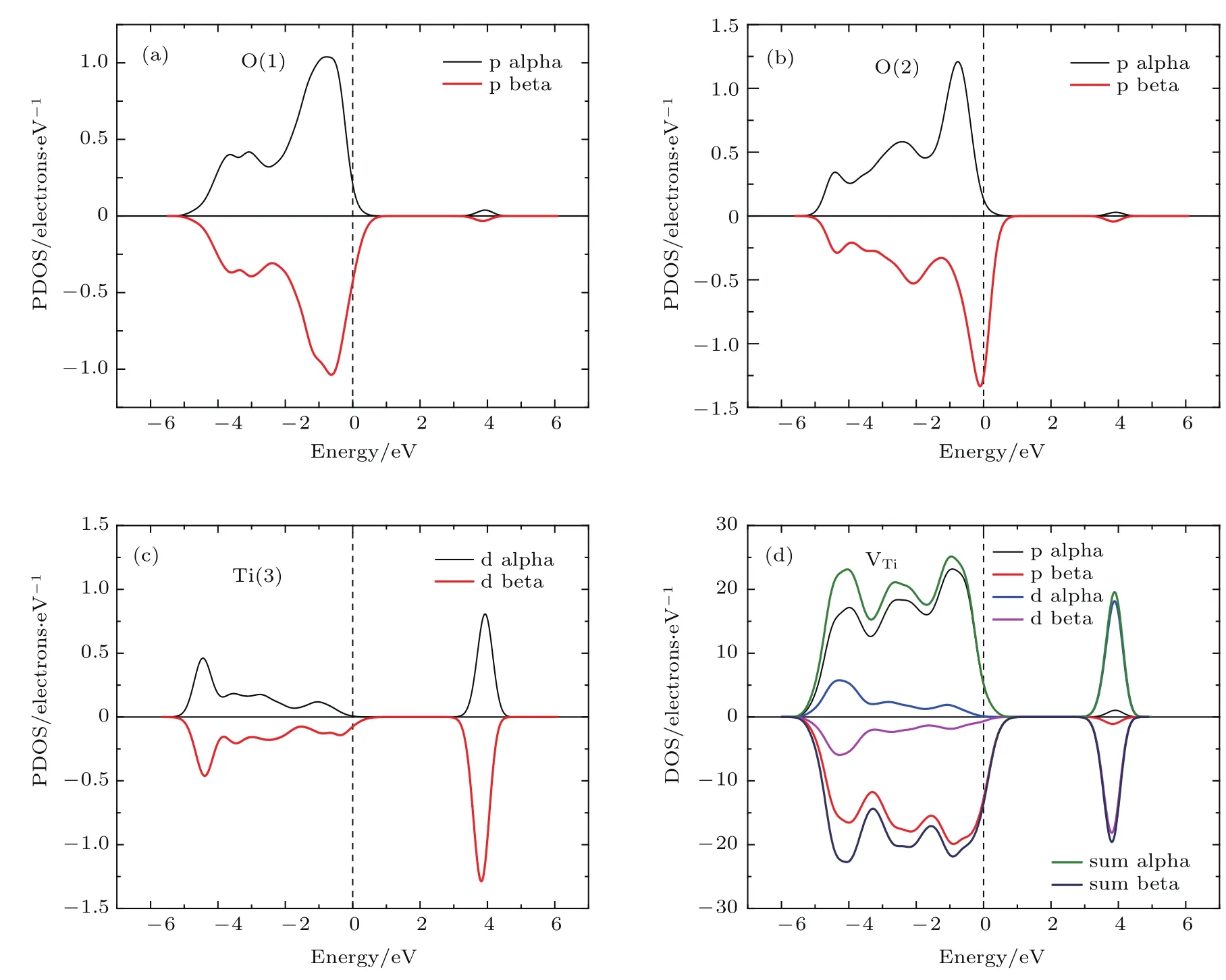
图6 (网刊彩色)局域原子(a)O(1),(b)O(2),(c)Ti(3)分态密度图和(d)VTi缺陷晶胞总态密度Fig.6.(color online)The partial density of states of(a)O(1),(b)O(2)and(c)Ti(3),and(d)the total density of states of the structure with one titaniumvacancy.

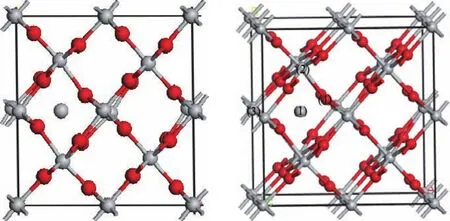
图7 (网刊彩色)弛豫后钛间隙缺陷(Tiin)晶胞结构图Fig.7.(color on line)Schematic d iagrams of the structure with one titaniuminterstitial defect after the relaxation.

由于系统稳定性要求相互作用能量尽量小,一个中性钛原子处于间隙空位时将自发地被氧化为Ti3+,成为3d壳层上有一个电子的模型.而多余的三个电子将转移至周围Ti4+原子的3d或4s轨道上,并与周围O原子的2p轨道重叠,发生强烈的杂化作用.由图7中Ti(3)原子的态密度的变化可知,第一个缺陷能级有可能是因为Tiin引入的3个电子破坏了八面体结构,电子态与畸变晶格相互作用产生极化子效应[41],也就是说当晶格结构变化使对称性降低,有可能使d轨道中二重简并被去除,转移电子将填充在能量较低的轨道上,进而导致3d或4s轨道发生强烈的变化引起的,因此Tiin缺陷中的磁性大多由Ti3+贡献.实验上,Ti3+离子处于价带顶上约2 eV位置处,距离导带底以下1 eV的间隙态,所以可认为第二个缺陷能级主要由被氧化和被还原的Ti3+离子引入.从图8(a),(c),(d)可发现,Tiin原子的束缚电子几乎完全被局域在自身和邻近钛原子的3d轨道上,邻近的O原子也因轨道杂化作用使2p轨道发生变化.

引入Tiin后晶体的费米面上升,这与Tiin原子施主杂质的特性相符,晶体将转变为n型简并半导体.Tiin晶胞总磁矩主要来自Ti原子和局域电子的贡献,总磁矩为3.91µB.

图8 (网刊彩色)局域原子(a)Ti(1),(b)O(4),(c)Ti(2),(d)Ti(3)分态密度和(e)Tiin缺陷晶胞总态密度Fig.8.(color on line)The partial density of states of(a)Ti(1),(b)O(4),(c)Ti(2),and(d)Ti(3),and(e)the total density of states of the structure with one titaniuminterstitial.

Oin原子极其不稳定,容易从周围原子获得电子形成O2逃逸,在文献[30]中也认为对于负电性氧间隙缺陷,只有处于二聚物状态才较为稳定.当一个氧原子位于八面体中心时,周围的钛原子将被吸引,氧原子则被向外排斥.由电荷布居数可知,引入Oin使得结构图9中(1)号位置的O原子的电负性增加,布居数由−0.72变为−0.77,结构图9中(2)号位置的O原子的电荷布居数仅为−0.3,间隙周围的Ti原子的正电性增强,结构图9中(3)号位置Ti原子的电荷布居数由1.45变为1.52.

图9 (网刊彩色)弛豫后氧间隙缺陷(Oin)晶胞结构图Fig.9.(color on line)Schematic diagrams of the structure with one oxygen interstitial defect after the relaxation.

图10 (网刊彩色)局域原子(a)O(1),(b)Ti(3),(c)O(2)的分态密度和(d)Oin缺陷晶胞总态密度Fig.10.(color on line)The partial density of states of(a)O(1),(b)Ti(3),and(c)O(2),and(d)the total density of states of the structure with one oxygen interstitial.

从图10(d)可知,Oin缺陷会在价带顶约1.2 eV处引入一个上下对称的过渡缺陷能级.由图10(a)和图10(c)的态密度图和布居数变化可知,该能级可能是由Oin原子与周围晶格O原子组成O—O结构形成σ*轨道的贡献[42].从图10(b)也可以看出,Oin原子周围的Ti原子的d轨道电子因杂化作用而引入了微小的缺陷态.由于设定Oin原子为中性粒子,晶格经充分弛豫后费米面稍微下降,但上下自旋仍然对称,系统总磁矩为零.

3.2 Ocom,Ticom复合缺陷

在超晶胞中同时引入一个VO缺陷与一个Oin原子,且在同一原胞内时,晶格经充分弛豫后,间隙原子将与空位复合,晶格将会有轻微的膨胀,其态密度和带间隙与完美晶体一致.因此本文将空位与间隙原子放置在不同的原胞中,如图11所示.晶格经弛豫后,由于氧空位的存在,局域电子的分布使间隙氧原子向O(6)靠拢.同时Ti(1),Ti(4)和Ti(7)将被其吸引,周围其余氧原子被排斥.由图12(i)可知,由于VO与Oin均为施主杂质,因此费米面将升高至导带底,同时VO与Oin将在导带底引入缺陷态,此缺陷态由O2p与Ti 3d轨道电子共同杂化组成.将图12中的分态密度与图4和图10对比可知,VO与Oin引入的缺陷态相互杂化,杂化后总密度态的自旋极化现象仍保持由VO附近的Ti原子贡献.由于复合缺陷计算的超晶胞大小与单个VO缺陷的超晶胞大小一致,因此总磁矩大小无明显差异[10,43],为1.63µB.Ocom的铁磁性特性与实验室通过贫氧条件生长晶体[28,44]或者通过O辐照[45]等获得的TiO2的铁磁性相符合.

图13为弛豫后钛空位与钛间隙复合缺陷(Ticom)晶胞结构图.由Ticom的态密度计算可知,因为Ti的核外电子数较O原子的多,当VTi与Tiin的距离与前文计算的VO与Oin复合缺陷的距离一致时,晶格经充分弛豫后,虽然缺陷的几何位置并没有重合,但VTi与Tiin复合缺陷的态密度已经与VTi或Tiin单个缺陷引入时的态密度截然不同,而是十分接近完美晶胞的态密度,如图14所示.

为进一步加大两种缺陷的距离,通过计算1×1×3超晶胞发现,VTi与Tiin原子在超晶胞中以反铁磁方式耦合.由于VTi与Tiin原子引入磁矩大小不一,因此超晶胞仍然表现出一定的铁磁特性.通过离子注入技术或通过调节TiO2晶体生长中的O或Ti的浓度,可使VTi与Tiin浓度出现偏差,使TiO2晶体获得由VTi或Tiin引入的铁磁性.再者VTi或Tiin的存在将会降低周围原子的形成能,使晶体更容易形成其他缺陷从而引入铁磁性.

同时在超晶胞中引入两个VO,VTi或Tiin来验证铁磁耦合的性质,计算铁磁性耦合的总能量EFM与反铁磁性的总能量EAFM.这三种缺陷的EFM比EAFM分别低317.6,813.3,238.5meV,较小的缺陷浓度时,这些能量比报道的Cu注入ZnO的能量差(42meV)高[46−48],结合平均场近似中的海森伯模型居里温度估算公式kBTC=2∆E/3x[1],其中kB为玻尔兹曼常数,TC为居里温度,x为磁性粒子浓度,∆E为EFM与EAFM的能量差,可知三种缺陷引入的铁磁性的居里温度分别为579.4,785.8,460.9 K,均为室温以上.

图11 (网刊彩色)弛豫后氧空位与氧间隙复合缺陷(Ocom)晶胞结构图Fig.11.(color online)Schematic diagrams of the structure with a complex defect of one oxygen vacancy and one oxygen interstitial after the relaxation.

图12 (网刊彩色)局域原子(a)O(2),(b)O(8),(c)O(3),(d)O(6),(e)Ti(1),(f)Ti(7),(g)Ti(4),(h)Ti(5)的分态密度和(i)Ocom缺陷晶胞总态密度Fig.12.(color on line)The partial density of states of(a)O(2),(b)O(8),(c)O(3),(d)O(6),(e)Ti(1),(f)Ti(7),(g)Ti(4),(h)Ti(5),and(i)the total density of states of the structurewith one oxygen interstitial and one oxygen vacancy.

图13 (网刊彩色)弛豫后钛空位与钛间隙复合缺陷(Ticom)晶胞结构图Fig.13.(color on line)Schematic d iagrams of the structu re with a complex defect of one titaniumvacancy and one titaniuminterstitial after the relaxation.

图14 (网刊彩色)局域原子的态密度和Ticom缺陷晶胞总态密度Fig.14.(color on line)The partial density of states and the total density of states of the structure with a complex defect of one titaniuminterstitial and one titaniumvacancy.

4 结 论

采用第一性原理的平面波超软赝势方法,并使用GGA+U方法来调整带隙,分别计算了TiO2的四种本征缺陷VO,VTi,Tiin,Oin与复合缺陷Ocom,Ticom的几何结构变化、布居数变化及态密度分布.计算结果表明,导致晶体转变为n型半导体的VO和Tiin的O2p与Ti 3d轨道杂化都会引起自旋极化,从而引入铁磁特性,其引入磁矩大小分别为1.62µB与3.91µB.使晶体转化为p型半导体的VTi在O2pπ窄带上形成空态,极化引入的磁矩为2.47µB.而Oin会在带隙中引入一个缺陷态,但是向上与向下自旋态密度仍然对称,且费米面基本不变.Ocom复合缺陷使费米面上升的程度比单个氧空位条件下的大,模拟超晶胞的态密度体现了VO与Oin的杂化,但保持了氧空位引入的铁磁特性,大小为1.63µB.Ticom中两种缺陷以反铁磁特性耦合,由于VTi与Tiin引入的铁磁特性不一致,因此超晶胞仍有一定的磁矩.

通过铁磁性耦合的总能量EFM与反铁磁性的总能量EAFM的计算,可知三种引入铁磁特性的本征缺陷均为铁磁性耦合,且居里温度高于室温.这些模拟计算结果对分析辐照或掺杂金红石型TiO2的磁性来源有一定的参考意义.

[1]Dietl T,OhnoH,Matsukura F,Cibert J,Ferrand D 2000Science287 1019

[2]MatsumotoY,Murakami M,ShonoT,Fukumu ra T,Kawasaki M,Ahmet P,ChikyowT,Koshihara S,Koinuma H2001Science291 854

[3]Higgins J S,Shinde S R,Ogale S B,Venkatesan T,G reene R L 2004Phys.Rev.B69 073201

[4]Toyosaki H,Fukumu ra T,Yamada Y,Naka jima K,ChikyowT,Hasegawa T,Koinuma H,KawasakiM2004Nat.Mater.3 221

[5]Chambers SA,W ang C M,Thevuthasan S,D roubay T,Mccready D E,Lea AS,Shutthanandan V,W indisch C F 2002Thin Solid Films418 197

[6]Hong N H2006J.Magn.Magn.Mater.303 338

[7]Pau l S,Choudhury B,Choudhu ry A2014J.Alloy.Compd.601 201

[8]KimD H,Yang J S,KimY S,KimD W,Noh TW,Bu S D,KimY W,Park Y D,Pearton S J,JoY,Park J G 2003Appl.Phys.Lett.83 4574

[9]Kang S H,Quynh HN T,Yoon S G,KimE T,Lee Z,Radmilovic V 2007Appl.Phys.Lett.90 102504

[10]Shu tthanandan V,Thevu thasan S,Heald SM,D roubay T,Engelhard MH,Kaspar TC,Mccready D E,Saraf L,Chambers SA,Mun BS,Hamdan N,Nachimuthu P,Tay lor B,Sears R P,Sinkovic B2004Appl.Phys.Lett.84 4466

[11]G riffi n KA,Pakhomov AB,W ang C M,Heald S M,Krishnan KM2005Phys.Rev.Lett.94 157204

[12]Santara B,Pal B,Giri P K2011J.Appl.Phys.110 114322

[13]Pereira L C J,Nunes MR,MonteiroOC,Silvestre AJ 2008Appl.Phys.Lett.93 222502

[14]Stausholm-Møller J,Kristoff ersen HH,Hinnemann B,Madsen G KH,Hammer B2010J.Chem.Phys.133 144708

[15]Shi L B,Wang Y P 2016J.Magn.Magn.Mater.405 1

[16]Zarh ri Z,Houmad M,Ziat Y,E l RhazouaniO,Slassi A,Benyoussef A,E l Kenz A2016J.Magn.Magn.Mater.406 212

[17]KimD,Hong J,Park Y R,KimKJ 2009J.Phys.:Condens.Matter21 195405

[18]Máca F,Kud rnovský J,D rchal V,Bouzerar G 2008Appl.Phys.Lett.92 212503

[19]Yang K,Dai Y,Huang B,Feng Y P 2010Phys.Rev.B81 033202

[20]Iddir H,Ğüt S,Zapol P,Browning N D 2007Phys.Rev.B75 073203

[21]Na Phattalung S,Smith MF,KimK,Du MH,W ei S H,Zhang S B,Limpijumnong S 2006Phys.Rev.B73 125205

[22]W ang M,Feng M,ZuoX 2014Appl.Surf.Sci.292 475

[23]Peng H2008Phys.Lett.A372 1527

[24]Mattioli G,Alippi P,Filippone F,Caminiti R,Amore Bonapasta A2010J.Phys.Chem.C114 21694

[25]D iebold U2003Surf.Sci.Rep.48 53

[26]de G raef M,Mchenry ME 2007Structure of Materia ls:An In troduction toCrysta llography,D iff raction and Symmetry(Cambridge:Cambridge University Press)p363

[27]Santara B,G iri P K,Imakite K,Fujii M2014J.Phys.D:Appl.Phys.47 215302

[28]Morgan BJ,Watson G W 2010J.Phys.Chem.C114 2321

[29]FakhimLamrani A,Belaiche M,Benyoussef A,E l Kenz A,Said i E H2010J.Magn.Magn.Mater.322 454

[30]Lee HY,C lark S J,Robertson J 2012Phys.Rev.B86 075209

[31]Nolan M,E lliott SD,Mu lley J S,Bennett R A,BashamM,Mu lheran P 2008Phys.Rev.B77 235424

[32]Henderson MA,Epling W S,Peden C HF,Perkins C L 2003J.Phys.Chem.B107 534

[33]Yang S,Halliburton L E,Manivannan A,Bunton P H,Baker D B,KlemmM,Horn S,Fu jishima A2009Appl.Phys.Lett.94 162114

[34]Santara B,G iri P K,Imakita K,Fu jiiM2013Nanoscale5 5476

[35]Yosida K1998Theory of Magnetism(Berlin:Springer-Verlag)pp87–89

[36]ZhaoL,Park SG,Magyari Köpe B,N ishi Y 2013Math.Compu t.Model.58 275

[37]Zhang Y,Qi Y Y,Hu Y H,Liang P 2013Chin.Phys.B22 127101

[38]Rumaiz AK,Ali B,Cey lan A,Boggs M,Beebe T,Shah S I2007Solid State Commun.144 334

[39]Coey J MD,Stamenov P,Gunning R D,Venkatesan M,Paul K2010NewJ.Phys.12 053025

[40]Finazzi E,D i Valentin C,Pacchioni G 2009J.Phys.Chem.C113 3382

[41]Lany S,Zunger A2009Phys.Rev.B80 085202

[42]Kamisaka H,Yamashita K2011J.Phys.Chem.C115 8265

[43]Mu lheran P A,Nolan M,Browne C S,BashamM,Sanville E,Bennett R A2010Phys.Chem.Chem.Phys.12 9763

[44]Koud riachova M2007Phys.Status Solidi C4 1205

[45]Zhou S,Čžmár E,Potzger K,Krause M,Talu t G,HelmM,Fassbender J,Zvyagin S A,Wosnitza J,Schmid t H2009Phys.Rev.B79 113201

[46]Lai L L,Wu JM2015Ceram.Int.41 12317

[47]Buchholz D B,Chang R P H,Song J Y,Ketterson J B2005Appl.Phys.Lett.87 082504

[48]Ye L H,Freeman AJ,Delley B2006Phys.Rev.B73 033203

PACS:71.15.Mb,73.20.At,75.10.–b,75.50.PpDOI:10.7498/aps.66.037101

Afi rst-principles study on magnetic properties of the intrinsic defects in ru tile TiO2∗

Lin Qiao-Lu1)LiGong-Ping1)†Xu Nan-Nan1)Liu Huan1)Wang Cang-Long2)

1)(School of Nuclear Science and Technology,Lanzhou University,Lanzhou 730000,China)2)(Institu te ofModern Physics,Chinese Academy of Sciences,Lanzhou 730000,China)(Received 2 September 2016;revised manuscript received 12 October 2016)

The TiO2based diluted magnetic semiconductors(DMSs)have aroused the considerable interest as one of the promising candidates for the spintronic devices accommodating both charge and spin of electrons in a single substance.Unfortunately,however,throughout most of the pub lished papers,the question howtoclearly elucidate the role of defects which may be played in the experimentally observed roomtemperature ferromagnetism(RTFM)remains open,especially after a newconcept of d0ferromagnetism.In such a case,tofurther understand this issue and alsotoexplore the origin of the RTFMin rutile TiO2,we here fi rst performa fi rst principles calcu lation on the magnetic properties of the intrinsic defects,namely oxygen vacancy(VO),Ti vacancy(VTi),Ti interstitial(Tiin),oxygen interstitial(Oin)and twocomplex defects of VO+Oinand VTi+Tiin.Combining the density functional theory and the Perdew-Burke-Ernzerhof functional of the generalized gradient approximation,we calculate various model structures of rutile TiO2constituted by 48-atom2×2×2 supercell.The cutoff energies in these calculations of the planewave basis are all set tobe 340 eV and the Monkhorst-Pack scheme k points are set tobe 3×3×4 for an irreducib le Brillouin zone.The convergence threshold for self-consistent field iteration is 0.1455× 10−6eV/atom.Structural relaxation is taken intoaccount in each of all calculations.It is found that each defectwe created in the structure leads toa lattice expansion and that the positive value for spin upand the negative value for spin down of the density of states(DOS)of the structure without defect are symmetric,suggesting that the perfect rutile TiO2lattice is non ferromagnetic.For the systemwith one VO,the total energy of the spin-polarized systemis 200 meV lower than that of the non-spin-polarized system,which indicates ferromagnetic behavior in this system.The defect brings in an impurity state near Fermi level located at about 0.7–1.0 eV down belowthe conduction band,resu lting in an excess of spin upover spin down for the presences of the twolocalized electrons left by the vacancy.At this point the supercell bears amagneticmoment of about 1.62µB.In contrast,VTialsobrings in an impurity state near Fermi level but above the valence band,which reveals a p-type characteristic semiconductor nature.Since a lower total energy requiresmore spin-upelectrons,the asymmetric DOS induces amagneticmoment of 2.47µB.W hen a neutral Tioccupies an interstitial lattice site,the systemrequires it tobe oxidized intoa Ti3+ion toincrease the stabilization of the system.The three delocalized electrons tend tooccupy the 3d or 4s orbital of the neighbor Ti4+ions and then have strong exchange interactions with the 2pelectrons of the local Oatom.This can distort octahedral symmetry and give rise toa ferromagnetic moment of 3.91µB.Oindefect in the supercell is extremely unstable.It can easily be reduced and escape fromthe host in terms of an oxygen molecule sothat the systemis in a manner similar tothe perfect lattice,showing noferromagnetism.It is interesting tonote that the properties of the systemwith the complex defect of one VOand Oinare similar tothat of the structure with one VOand themagnetic moment of this systemis 1.63µB.For the Ticomcomplex defect,our results point out the fact that themagnetic properties of the supercell are related tothe distance between VTiand Tiin.The spin upand spin down states are symmetric when they are close toeach other,while,in addition tosome ferromagnetic behavior,the systemmainly exhibits antiferromagnetismwhen the distance increases.

fi rst-principles,intrinsic defect,density of states,magnetization

10.7498/aps.66.037101

∗国家自然科学基金(批准号:11575074,11304324)和山东大学晶体材料国家重点实验室开放基金(批准号:KF1311)资助的课题.

†通信作者.E-mail:ligp@lzu.edu.cn

*Project supported by the National Natural Science Foundation of China(G rant Nos.11575074,11304324)and the State Key Laboratory of Crystal Materials at Shandong University Open Foundation,China(G rant No.KF1311).

†Corresponding author.E-mail:ligp@lzu.edu.cn