高温等离子体的状态方程及其热力学性质

汤文辉徐彬彬 冉宪文 徐志宏

(国防科学技术大学理学院,长沙 410073)(2016年10月17日收到;2016年12月17日收到修改稿)

专题:高压下物质的新结构与新性质研究进展

高温等离子体的状态方程及其热力学性质

汤文辉†徐彬彬 冉宪文 徐志宏

(国防科学技术大学理学院,长沙 410073)(2016年10月17日收到;2016年12月17日收到修改稿)

高温下等离子体的状态方程及其热力学性质在天体物理、可控核聚变以及武器设计与破坏效应等领域有着广泛应用.本文主要回顾了高温等离子体在不同状态区域的状态方程的理论模型和处理方法.对于理想等离子体,离子之间的相互作用可以忽略,其状态方程较简单,已趋于完善.在超高温下,原子完全电离,离子和电子都可以采用理想气体状态方程描述;当温度不太高时,离子部分电离,可以采用Saha方程及其修正模型描述;原子在高度压缩状态下,其状态方程可以采用Thomas-Fermi模型及其改进模型得到.对于非理想等离子体,离子之间存在强耦合,还没有单一的理论模型能够在任意密度和温度范围内对离子之间的相互作用进行统一描述.量子分子动力学方法原则上可以在较大温度密度范围内给出可靠结果,但由于计算量太大以及高温下的计算存在收敛问题,也较难应用到温度较高的稠密等离子体区域.半经验的经典分子动力学方法虽然简单、计算量小,但只能在一定的区域范围内给出较精确的状态方程结果.在不同温度密度区域内采用不同的计算模型,再在空白区域进行插值从而得到全局状态方程在目前不失为一种简单有效的方法.

高温等离子体,状态方程,热力学性质

1 引 言

自然界中大约90%—95%的可观测物质处于极端高温高压条件下[1].太平洋底部(海平面下11 km处)压强为0.12 GPa;地球中心处的压强为360 GPa,温度为0.5 eV(1 eV=11604.5 K),密度约为10—20 g/cm3;木星中心压强约为4—6 TPa,温度约为2 eV,密度约为30 g/cm3;太阳中心压强为2.4×107GPa,温度为1.6×103eV,密度约为150 g/cm3;白矮星压强为1012—1018GPa,密度为106—109g/cm3,温度为103eV.在惯性约束聚变(ICF)中,中心点火需要氘氚(DT)热斑温度达到5 keV以上,密度100 g/cm3以上,压强达到1.5×107—2.0×107GPa.目前已知的自然界的物态范围大致如图1[1]所示(1 bar=105Pa).然而,在实验室条件下只能产生相对较低的压强和温度.静高压加载能达到550 GPa的压强[2],结合激光加热技术可使实验温度能够达到3000 K以上[3].动高压加载虽然能产生104GPa的瞬态高压,但持续时间短,实验测量非常困难,测量结果误差较大[4].事实上,人们真正了解的物质状态范围只是图1中很小的一个区域,研究更大温度密度范围的物质状态需要发展更先进的实验手段和理论方法.

状态方程是描述物质系统中各状态变量之间关系的函数表达式,反映物质在一定热力学条件下的宏观性质[1,4].近代自然科学和工程技术中的大量实际问题,比如天体物理、恒星以及行星内部构造、惯性约束聚变、武器系统的设计及其破坏效应等问题,都涉及到物质处于高温、高压、高密度等极端条件,要对这些问题进行研究,就需要了解物质在各种极端条件下的状态方程及其热力学性质[5].

众所周知,高温条件下的物质以等离子体的形式存在.随着科学技术的发展以及国防科技的驱动,等离子体的热力学性质及其描述方法已成为目前的研究热点之一.然而,等离子体的热力学性质及其描述方法与其所处压强和温度状态密切相关,难度很大.为了便于人们对等离子体的热力学性质开展深入研究,本文在文献报道的基础上对高温(1 eV以上)等离子体的状态方程模型及其热力学性质进行了综述.

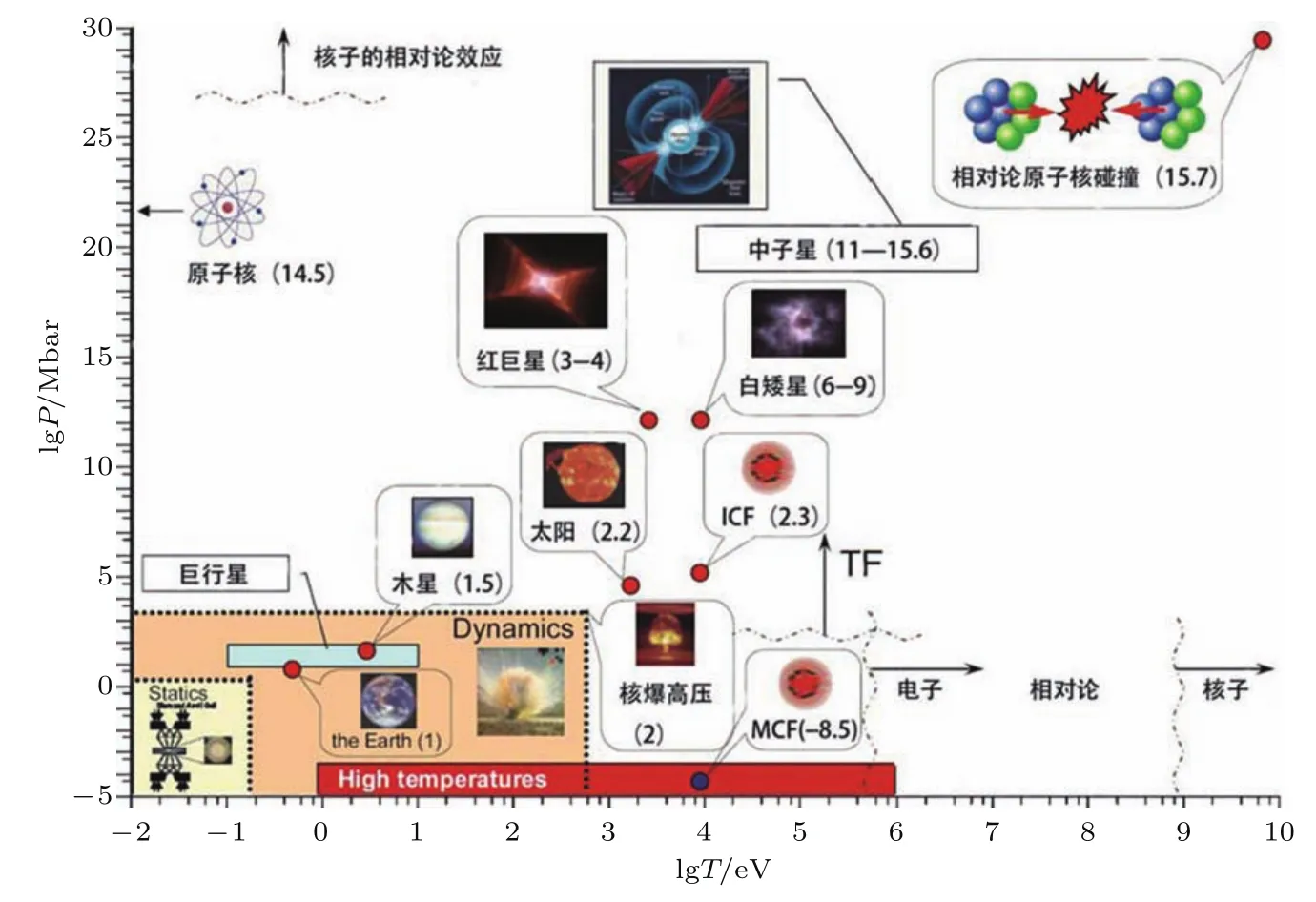
图1 自然界和实验室中的物态范围[1],图中括号里的数字表示密度的对数值,密度单位为g/cm3;“Statics”区域对应静高压实验所能达到的温度压强范围,“Dynamics”区域表示动高压加载实验所能达到的温度压强范围Fig.1.Extreme states in natu re and in the laboratory[1],the numbers in parentheses ind icate the logarithmof density(g/cm3).The “statics” domain corresponds tostatic techniques for high-pressure production,the“dynamics” domain tothe dynamic ones.

2 等离子体状态区域的划分

等离子体可以根据离子间相互作用的强弱划分为理想等离子体和非理想等离子体[6].定义ΓD为离子之间相互作用能与离子动能的比值,ΓD可用于评估离子之间耦合的强弱,称为离子耦合系数.ΓD≪1表示离子之间的相互作用非常小,这时可以认为等离子体是理想等离子体;ΓD～1表示离子之间的相互作用不容忽略,等离子体是非理想等离子体;ΓD≫1时,离子间存在较强的相互作用,离子间的相互作用能占主导地位.

另一方面,根据粒子量子效应的强弱可以将等离子体分为强简并等离子体和弱简并等离子体,粒子简并度参数可用α表示如下:

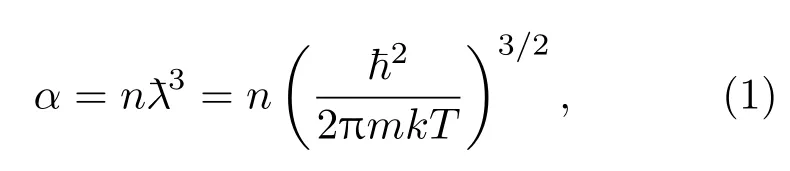
式中,n是粒子数密度,λ¯是电子德布罗意波长,ħ是约化Planck常数,m是粒子质量,k是Boltzmann常数,T是温度.α=n3≪1表示粒子间距远大于粒子的德布罗意波长,粒子处于非简并或者弱简并态,量子效应不明显,这时粒子可以作为经典粒子处理,遵循经典的Boltzmann统计.当粒子间距较小时,粒子处于强简并态(α≫1),服从Fermi量子统计.相对于电子,离子的质量较大,德布罗意波长非常小,因此离子的量子效应只有在极低温情况下才需要考虑.对于质量最小的氢离子,在固体密度状态下,温度需要降低到几十开尔文(K),氢离子的量子效应才需要考虑.对于惯性约束聚变中心点火热斑,氘氚燃料被压缩到原来固体密度的1000倍以上,温度到达5 keV以上[7],由于氘氚离子满足α≪1的条件,因此中心氘氚热斑不需要考虑氘氚离子的量子效应,但对于电子,其量子效应不能忽略.

为了方便,我们根据离子耦合系数以及电子简并度参数的大小,把高温等离子体分成四个区域进行讨论,如图2所示.I区和II区分界线是原子完全电离所需温度,II区和IV区是根据离子相互作用耦合强弱划分的,I区和III区是根据电子简并强弱划分的.由于不同元素完全电离温度不一致,图2中的区域划分主要适用于低Z元素,对于高Z元素,由于原子完全电离所需温度增加,因此I区和II区的分界线需要适当上移.I区是完全电离的等离子体,在温度非常高的情况下,原子中所有电子电离,这时粒子之间的相互作用可以忽略不计,电子也处于非简并状态(ΓD≪1,α≪1),满足经典Boltzmann统计,此区域的等离子体中电子和原子核都可以采用理想气体状态方程描述.II区是部分电离弱耦合等离子体,温度不是特别高,部分电子处于自由态,部分处于束缚态.此区域密度较低,电子和电子之间以及电子和离子之间的相互作用较弱(ΓD≪ 1,α≪ 1),但在靠近 ΓD=1的区域,需要考虑粒子间的远程Coulomb相互作用.III区是强简并等离子体,物质密度非常高,原子处于高度压缩状态,电子分布在原子核周围,对原子核产生屏蔽,原子核与原子核的相互作用可以忽略,电子处于强简并状态(ΓD≪1,α≫1).IV区是强耦合等离子体,物质密度较高,温度相对较低,离子之间耦合作用非常强,电子处于部分电离部分简并状态(ΓD≫1或者ΓD～1,α～1).I区、II区以及III区的等离子体由于离子间相互作用可以忽略不计,因此可以当作理想等离子体处理,现有的理论模型能够较好地对这些区域的等离子体状态方程进行描述,而IV区是强耦合等离子体,离子之间的相互作用还没有一个单一的理论模型能够在任意密度和温度范围内进行统一的描述.

原子序数为Z的离子间Coulomb作用能为

式中

其中,M为原子摩尔质量,ρ为密度,NA为Avogadro常数,e为电子电荷量,r是粒子间的平均距离,r～ n−1/3.

单个粒子的平均动能为

对于I区和II区的稀薄理想等离子体,ΓD≪1.如果离子之间主要是Cou lomb相互作用,则耦合系数满足条件

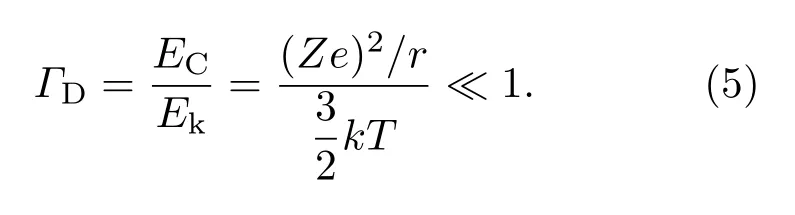
经过变换,得到满足稀薄理想等离子体的条件为

式中温度单位为K.由(6)式可知,气体在常态密度情况下,温度只需要几个eV就可以满足稀薄气体条件;对于锂、铍等较轻的元素,常态密度下,温度需要达到几十eV才能满足稀薄气体条件;对于重元素,则需要上百eV的温度才能满足稀薄气体条件.对于完全电离的稀薄等离子体,电子和离子都满足经典Boltzmann条件,这时可以把电子和离子都作为理想气体处理.对于温度较低的稀薄理想等离子体,其状态方程和电离度相关,而电离状态可以采用Saha方程[8]进行描述.虽然带电粒子间的长程Coulomb作用能相对粒子动能较小,但Cou lomb相互作用引起附加的自由能,会导致电离能减小,因此在密度稍高或者温度较低的情况下,也就是ΓD≪1条件满足较弱的情况下,需要考虑粒子间长程Coulomb作用的影响,这时的状态方程可以采用Debye-Hückel模型[9]计算.

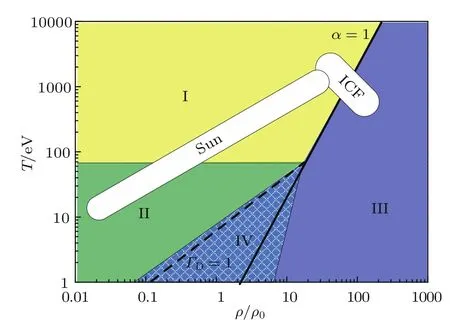
图2 温度密度平面上等离子体区域的划分,其中,I区为完全电离等离子体,II区为部分电离区弱耦合等离子体,III区为强简并等离子体,IV区为强耦合等离子体;图中粗实线是电子简并强弱分界线,即α=1,粗虚线表示离子耦合强弱分界线,即ΓD=1,细实线表示四个区域的分界线,Sun以及ICF分别表示太阳和惯性约束聚变条件下氢的同位素所处的大致区域Fig.2.D ivision of plasma on the density and temperatu re region:Iis the fu lly ionized plasma,IIis partly ionized and week coupling plasma,IIIis the strong degenerate plasma and IV is the strong coupling plasma.The thick solid lines are the boundary ofweak and strong degenerate of electron(α=1)and the thick dashed are the boundary ofweak and strong coupling of ion(ΓD=1).The thin solid lines are the boundary of four regions.Sun and ICF mean the regions of hyd rogen’s isotopes under the condition of sun and inertial con finement fusion.

III区为强简并等离子体,是原子被高度压缩所形成的.原子的内层电子被均匀挤压,电子处于强简并态,满足关系,电子的分布可以使用Thomas-Fermi(TF)模型[10,11]进行描述.TF模型认为原子中电子连续分布在原子核周围[12,13],原子核被连续的电子云所包围,电子是一团简并气体,并遵循Fermi量子统计.由于分布在原子核周围高密度电子的屏蔽作用,原子核与原子核之间的相互作用可以忽略.当原子中电子处于强简并状态时,费米能为Ek～2n2/3/(2m),于是ΓD正比于n−1/3.粒子数密度n越大时,ΓD越小,因此电子强简并条件下的等离子体在高度压缩条件下也趋于理想等离子体.

对于IV区的强耦合等离子体,离子之间存在较强的相互作用(ΓD～1或者ΓD≫1).由于电子处于部分简并状态,这时单纯采用经典Boltzmann统计模型或者Fermi量子统计模型都不能正确地描述电子的统计状态.物质处于稠密状态时,相邻原子之间的距离非常小,离子间存在较强的相互作用,因此必须正确描述离子间的相互作用才能准确描述物质的热力学性质.分子动力学方法可以较好地描述粒子之间的相互作用,但前提是需要知道粒子之间的相互作用势.根据所使用的原子间相互作用势的不同,分子动力学方法可以分为两大类:一类是经典分子动力学方法(MD),粒子之间相互作用采用经验势或半经验势进行描述;而另一类是量子分子动力学方法(QMD),原子间相互作用势基于量子力学理论计算得到,比如基于密度泛函理论计算的分子动力学方法[14].两种分子动力学方法各有优缺点.经典分子动力学方法由于直接使用经验势,因此计算方法简单,计算量小;但由于不同物质的相互作用势差别较大,一种经验势一般只适用于一种原子系统或一部分系统,而且经验势也局限于一定的密度温度范围,因此使用某种经验势的经典分子动力学方法只适用于特定温度密度范围内的某些物质.量子分子动力学方法不用假设粒子间的相互作用势,而是由第一性原理计算原子相互作用势,所以具有普适性,但由于在高温时计算量较大,而且难以收敛,因此主要适用于温度不太高的状态.在计算电子结构时为了节约机时,量子分子动力学常采用赝势的方法,因此在温度较高时,电子跃迁和电子激发的处理也存在困难,这时需要采用一些半经验的分子动力学或改进的量子分子动力学模型来描述稠密物质的状态.总之,等离子体处于温稠密和热稠密状态时,难以采用单一的理论模型对其状态方程进行精确描述,一般需要采用多种理论模型相结合,各自描述一部分密度和温度范围,然后通过插值得到过渡段的状态方程.

3 高温稀薄等离子体

对于理想气体,不考虑原子之间的相互作用力,其状态方程可表示为

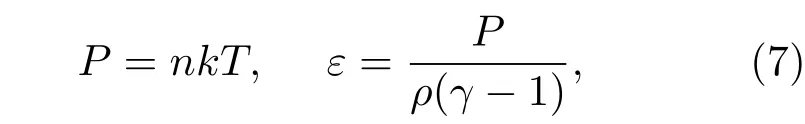
式中P为压强;ε为比内能;n为粒子数密度;γ为气体比热比,与气体的内部自由度相关,如果气体有q个自由度,则γ=1+2/q.对于单原子分子q=3,γ=5/3;对于双原子分子q=5,γ=7/5.

高温条件下,分子先离解成原子,随后原子电离成各级离子.分子的离解以及原子的电离都会导致气体的粒子数密度发生明显变化.当温度升高到原子完全电离(图2中I区),等离子体的粒子(包括离子与电子)数密度由原来的n变为(1+Z)n,Z为原子的核电荷数.因此,原子完全电离的高温稀薄等离子体状态方程可以表示为

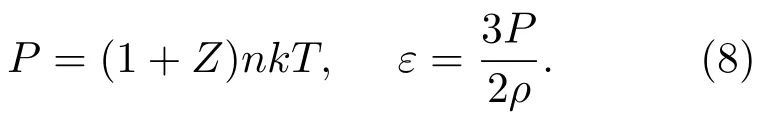
对于部分电离的稀薄等离子体(图2中II区),其状态方程可采用Saha方程[8]描述.温度不是很高时,原子并未完全电离,带电粒子的平均动能远远大于粒子之间的Coulomb相互作用能,这时Saha方程可以很好地描述其电离行为.Saha方程适用的范围是ΓD≪1,对于原子序数为Z的粒子,稀薄气体条件即是(6)式.在低密度或者高温情况下都可以满足Saha方程条件,但在密度较高或者温度较低情况下(图2中II区靠近IV区位置),电离气体系统中带电粒子间的长程Coulomb作用不可忽视.Coulomb相互作用引起附加的自由能,使电离能减小.对于这样的系统,必须对Saha模型添加Debye-Hückel近似进行修正.

3.1 稀薄电离气体的Saha模型

大部分分子在1 eV以上时已经离解为原子,有些原子已经发生了电离,随着温度的进一步升高,较重原子所组成的气体会多次电离.考察某种原子所组成的气体,单位质量气体中含有N个原子,单个原子的总能量为E=Ek+Q,其中Ek为单个原子的动能,包括离子以及电子的动能;Q为原子内电子的势能.在气体足够稀薄的情况下,电子遵循Boltzmann统计规律,这时气体中每一个粒子(包括中性原子、离子以及电子)的平均热能是(3/2)kT,因此N个原子系统总的热能为

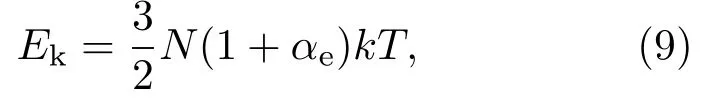
其中αe为平均电离度.

用Im表示第m次激发电子所必须消耗的能量,则从原子中激发m个电子需要消耗的总能量为

在给定温度T以及密度ρ的情况下,单位质量气体中含有N0个中性原子,N1个一次电离的离子,Nm个电离m次的离子,以及Ne个电子.此外电离m次的离子还具有电子激发能Hm,因此气体总的内能为

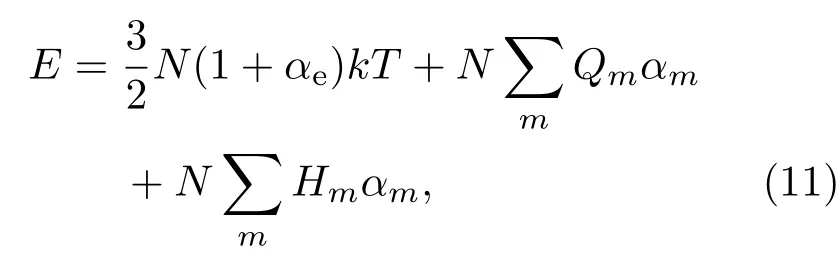
(11)式中,αe是气体的平均电离度,即Ne/N;αm是电离m次离子的浓度,表示为Nm/N.由于气体比较稀薄,在粒子之间相互作用可以忽略的条件下,所有粒子都可以当作理想气体,因此可以得到电离气体的压强为

气体的压强与总的粒子数密度相关,总的粒子数密度等于电子数密度与离子数密度之和.等离子体电离度越大,其压力越高.电离度可以通过原子数守恒、电荷守恒以及Saha方程联立求得

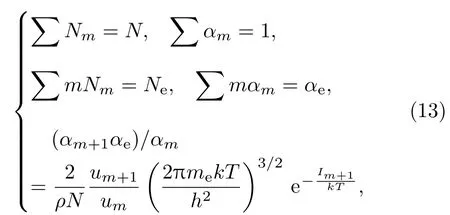
3.2 考虑辐射超高温等离子气体

当等离子体气体温度非常高或者密度非常低时,这时辐射压以及辐射能相对于气体的压强以及能量并不能被忽略,需要把辐射的能量以及压强加入到气体的能量和压强中.平衡辐射条件下,辐射的比能量等于辐射能量密度除以物质的密度,即

辐射压强可以表示为

辐射压和温度的四次方成正比,而根据(12)式,物质压和温度的一次方成正比,因此当温度超过一定范围之后,辐射压将完全占据主导地位.令辐射压等于物质压,可以得到两种压强平衡时温度和密度之间的关系式为

式中密度单位取g/cm3.对标准密度的空气来说,当空气温度超过100 eV时,辐射压起主要作用;对于密度为1 g/cm3的固体来说,辐射压要在温度达到几keV以上时才起主要作用.

如果辐射能流和物质能流为同一量级,这时辐射输运在能量输运过程中必须考虑.辐射能量以光速进行传播,而物质能量以物质的速度进行传播,在辐射温度不是很高的情况下,也需要对辐射能流进行考虑.同样令物质能流等于辐射能流,假设物质速度为光速的千分之一,则在固体密度条件下,当温度在几十eV时需要考虑辐射输运过程,这时不能单纯使用流体动力学过程描述物质的运动,而需要使用辐射流体动力学模型来考察物质的运动.

3.3 冲击压缩下的等离子体气体

在单次冲击压缩条件下,当冲击波强度足够大时,气体的极限压缩度可以表示为

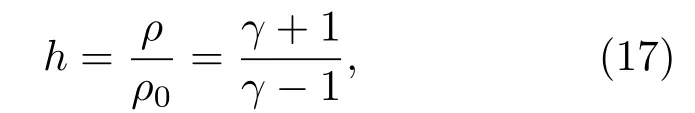
对于单原子理想气体,γ=5/3,h=4,即气体密度最多只能被压缩4倍;对于双原子理想气体,γ=7/5,h=6.可见,气体比热比γ越接近于1,其压缩度也就越大.

在冲击波压缩下,波后物质的压强、密度与比内能之间的关系由Hugoniot方程给出:

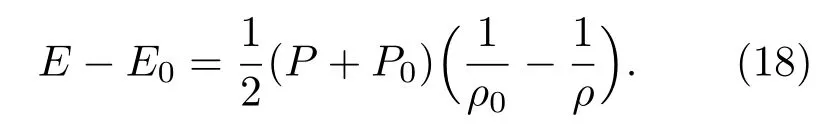
等离子体的内能可以分为两部分,即E=Ek+Q,其中Ek为粒子的平均动能,Q包含了粒子的势能以及粒子内部自由度的能量.由于压强只和粒子的平动动能相关,即P=(2/3)ρEk,代入(18)式,在强冲击波条件下,忽略冲击波波前压力P0和内能E0,将ρ/ρ0用h代替,得到

从(19)式可以看出,势能Q相对于热运动动能忽略不计(3Q/Ek≪1)时,单原子气体的压缩度最大值为4.在电离情况下,总的粒子数目增加,但(19)式表明,压缩度和总的粒子数密度没有关系,因此总粒子数目的增加并不会增加压缩度.另一方面,电离度增加会导致用于电离的能量损耗增加,也就是势能对总内能的相对贡献增加,因此原子在冲击压缩下发生电离时,会使气体变得更加容易压缩.随着原子最外层电子开始电离,到最外层电子全部电离,这个过程用于电离的能量所占总内能的比例增加,因此这个过程压缩度是增加的.在原子最外层电子(K层电子)全部电离而次外层电子(M层电子)还未开始电离时,随着冲击波强度的增加,在相当一段范围内离子不再发生电离(因为次外层电子电离能比最外层电子电离能大很多),势能Q保持不变,而温度升高成为内能增加的主要形式,因此Q/Ek会减小,从而导致压缩度降低.如果冲击波强度足够大,能够导致次外层电子电离,这时随着冲击波强度的进一步增加,次外层电子会像最外层电子一样一个个剥落,用于电离的势能相对贡献又增加,因此导致压缩度再一次增大.如果是重原子气体,原子含有多个壳层,则随着各层电子的依次电离,冲击压缩条件下的压缩度先增大再减小,然后又增大再减小.如果冲击压缩过后原子发生完全电离,随着冲击波强度进一步增加,会导致温度急剧上升,粒子的热运动动能急剧增加,而势能Q保持不变,因此压缩度最后会减小.在冲击波强度非常大的情况下,如果不考虑热辐射,根据(19)式,完全电离气体的压缩度也是趋近于4.

3.4 考虑粒子间Cou lomb作用的稀薄等离子体

对于满足理想等离子体条件较弱的稀薄等离子体,粒子之间的Coulomb相互作用相对于热运动能量虽然较小,但不能忽视.这时Coulomb相互作用可以采用Debye-Hückel模型进行计算.Debye-Hückel模型假定所有带电粒子的势场都是球对称的,带电粒子之间只考虑Coulomb作用力,但仍然假定Coulomb作用能仍远小于粒子的热运动动能,因此有

或者表示为

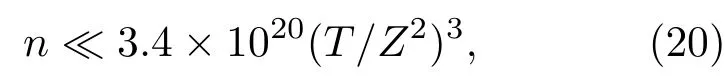
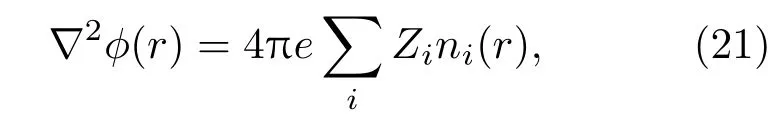
式中ϕ(r)表示r处的电势,ni(r)是r处第i种粒子的数密度,Zi是第i种粒子的电荷数.第i种带电粒子的势能可以表示为

由于粒子满足Boltzmann统计规律(稀薄电离气体条件下,电子和离子都可以看作经典气体),粒子数密度的空间分布为

式中ni0是电荷为Zi的粒子的平均数密度.(23)式后面约等号成立的条件是粒子Coulomb作用能相对于粒子的平均动能是小量.由于满足电荷守恒,把(23)式代入泊松方程(21)得到

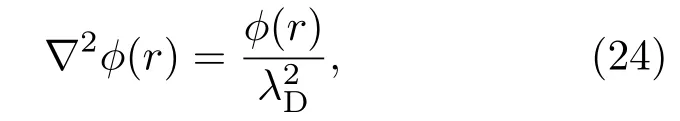
在粒子中心附近有r≪λD,因此有

式中第一项为中心粒子本身所产生的势,第二项ϕ′=Zie/λD是周围其他粒子在r处所形成的势.

2015年11月底，《中共中央国务院关于进一步推进农垦改革发展的意见》中要求，用3年左右时间，将国有农场承担的社会管理和公共服务职能纳入地方政府统一管理，基本完成农垦国有土地使用权确权登记发证任务。

在体积V中,等离子体的Coulomb相互作用能为所有粒子相互作用势的一半,利用(22)式有

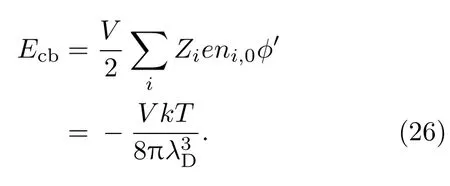
异性带电粒子存在吸引力作用,每个离子周围都有大量的电子,所以Coulomb作用能以及压强都是负值.Cou lomb作用影响气体的状态主要体现在两个方面,一个是减小气体的内能和压强,还有一个效应是降低电离能,从而使得电离更加容易发生.Coulomb相互作用中的电子并不是完全自由的,由于电子还在离子的势场中,其势能并不为0,而是负值,因此把电子从原子或者离子中电离出来需要消耗的电离能会下降.电离能的减小可以表示为

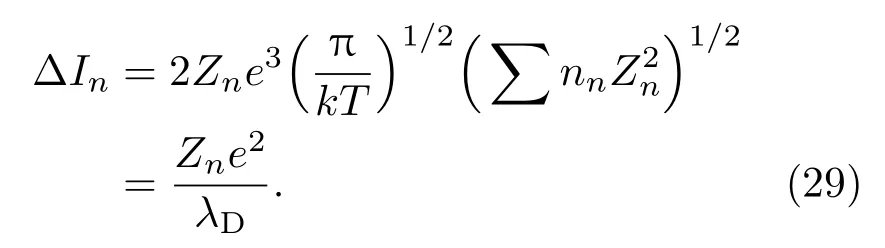
在较低温度下,∆In相对于kT可以忽略不计,但在上百eV高温下,∆In/In可以达到10%.在密度较高情况下,考虑粒子之间的远程Coulomb作用,压强和内能会减小,也会使得电子电离能下降,从而使电离更容易发生.

4 强简并等离子体

前面所讨论的电离气体,电子和离子都遵循经典的Boltzmann统计,但只有在温度相当高或者密度相当低的情形下,才能满足经典Boltzmann统计条件.物质在高度压缩条件下,原子内电子高度简并,这时必须考虑电子的量子效应.对于物质在高温高压条件下的物态性质,比较简洁方便的处理方法是采用TF模型[15].TF模型描述的是电子对压强和内能的贡献,原子核对压强以及内能的贡献可以采用理想气体状态方程描述,

式中,na为原子核数密度.

电子对内能的贡献包括电子的动能、电子与其他电子以及原子核之间的相互作用能.下面主要讨论电子对系统压强以及内能的贡献.

4.1 费米简并态自由电子气体

自由电子在低密度或者温度较高情况下服从经典的Boltzmann统计,但在温度较低或者密度较高的情况下,由于电子处于简并状态,其量子态必须要考虑.零温时,自由电子处于完全简并状态,在dVdp相空间的量子数为4πp2dpdV/3,由于电子有两个不同的自旋方向,因此在相空间内量子数还需要乘以2.根据泡利不相容原理,每一个确定的自旋方向的量子状态中只能有一个电子,假设体积V中N个电子紧凑地占据了动量从0到p0的量子态,因此有关系式

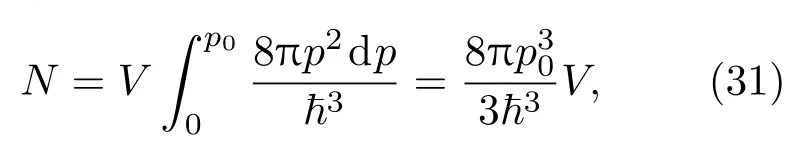
定义费米温度TF=ε0/k为

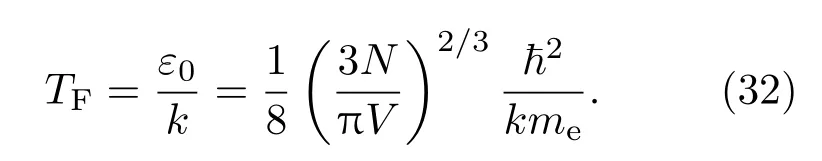
电子的简并程度也可以根据费米温度进行判断,如果电子温度T≫TF,则电子处于弱简并态或者非简并态,电子可以作为经典气体处理;如果T≪TF,则电子处于强简并状态,服从量子分布.比较(1)和(32)式有α∝(TF/T)3/2,可见α≪1与T≫TF是等价关系,都表示电子处于弱简并状态;而α≫1与T≪TF也是等价关系,表明电子处于强简并状态.因此,(1)式和(32)式都可以评判电子的简并程度,并且评判结果是一致的.

体积V中N个电子的动能为

根据热力学关系Td S=d E+P d V,零温下完全简并电子气体的压强为

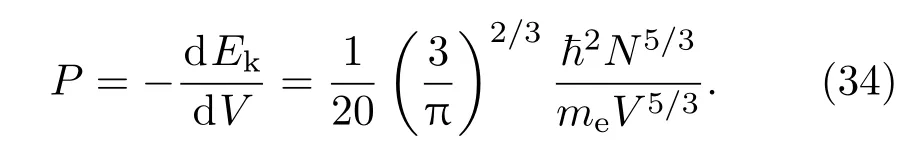
从(34)式可以看出,在极低温条件下,自由简并电子的压强正比于密度的5/3次方,而在超高温情况下,电子服从经典Boltzmann统计,这时可以采用理想气体状态方程描述,压强与密度的一次方成正比,这说明电子气体处于简并状态时更难压缩.高温压缩下原子中的电子并不是完全自由的,而是在原子核以及其他电子所形成的势场中运动,这时电子的行为可以使用TF模型进行描述.

4.2 TF模型

单个原子中电子在原子核周围服从Fermi-Dirac分布,分布函数为

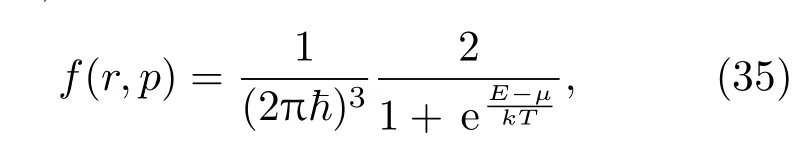
式中,µ是电子的化学势,E是电子的能量.在TF模型中,电子在原子核以及其他电子所产生的势场中运动,其能量主要包括动能以及在原子内的静电势能,E=p2/(2me)−eU(r),U(r)是r处的电势,p为电子的动量.利用电子的分布函数可以得到电子数密度为

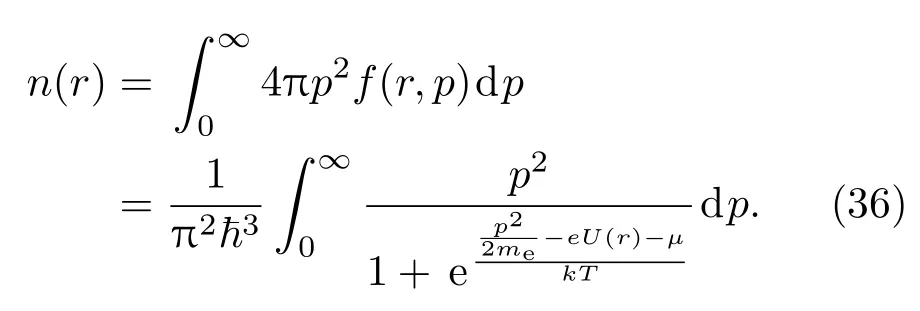
原子内电子总数等于核电荷数,即

(37)式称为电荷守恒条件,由此可得到化学势µ.

在电子数密度已知条件下,原子内的电势可以通过泊松方程得到

(38)式就是TF方程.TF方程是二阶微分方程,对其求解需要一定的边界条件.在原子中心附近,也就是半径趋向于0时,由于电子均匀连续分布在原子核周围,因此原子中心处的电势全部由原子核提供,这时的边界条件可以表示为

TF方程再加上两个边界条件可以封闭求解,从而得到TF模型下原子中的电子分布.由于电子的分布影响势场,而势场又会影响电子的分布,势场和电子分布耦合在一起,因此TF方程的解析解难以得到,一般采用数值计算或者近似方法求解.虽然TF方程没有解析解,但TF方程的解具有普适性质,只要温度和体积以TZ−4/3,VZ形式出现,则压强、内能、比热容以PZ−10/3,EZ−7/3,CVZ−1的形式出现,这意味着只要知道某种元素的TF状态方程,根据上面所得到的普适性质,可以得到任意元素的TF状态方程.对于多种原子所组成的物质,可以利用平均原子的概念得到其TF状态方程.平均原子序数和平均原子量可以表示为

式中xi是第i种原子数目所占总原子数目的百分比,Zi和Mi分别为第i种原子的原子序数和原子量.

TF模型不区分电子是否处于束缚状态,因此这也意味着物质的热力学性质和原子的壳层结构没有任何关系,只和原子序数相关.从TF模型的普适性也可以看出,在相同的密度条件下,随着温度升高,物质的压强和内能是随着原子序数的增加而单调增加的.由于不区分电子的壳层结构,温度的升高只是改变原子中电子密度的重新分布,因此电子势能的变化较缓慢,电子密度在原子体积中的分布更趋于均匀.在温度非常高的情况下,也就是电子温度远远大于费米温度(T≫TF),这时电子的简并性将被消除,等离子体从图2中的III区过渡到I区,这时的状态方程和完全电离理想气体状态方程一样,压强和密度成正比.

4.3 改进的TF模型

简单的TF模型只考虑了电子之间的Cou lomb相互作用,而没有考虑交换相互作用.电子是费米子,服从泡利不相容原理,其所引起的自旋平行电子之间的相互作用在计算电子在原子核周围的分布时需要考虑.Dirac[16]于1930年引入交换能对零温TF模型进行了修正,由此得到了Thomas-Fermi-Dirac(TFD)模型.Cowan和Ashkin[17]进一步将TFD模型推广到有限温度情况.TF模型对电子的能量只考虑了电子的动能、电子与原子核以及其他电子相互作用势能,TFD模型还考虑了电子与所有自旋平行电子的交换能.考虑交换能后电子分布函数可以表示为

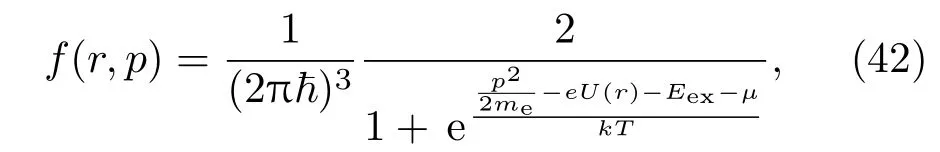
式中Eex是自由电子的交换能.由Bloch[18]估算得到的交换能表示为

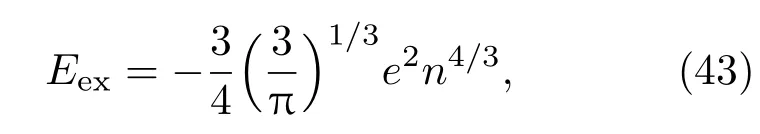
如果Eex～kT或者Eex≫ kT,则电子交换能对TF模型的修正非常明显,而在Eex≪ kT时,电子交换能可以忽略,这时温度需要满足的条件为T≫ 1.37×10−15n4/3.当物质处于固体密度时,温度需要几十甚至上百eV,电子交换项的影响才可以忽略不计.与TF模型结果进行比较,TFD模型的压强在低温下(几十eV以下)比TF模型要低,随着温度的升高,两者差别越来越小,最后会重合在一起.McCarthy[19]采用不同模型进行计算给出了铅在不同温度下压强随密度的变化,如图3所示[19].可以看出,零温(kT=0 eV)时,采用TFD模型得到的压强明显要比TF模型得到的压强低,10 eV时两者差别减小,在100 eV时已基本重合在一起.

图3 铅在100,10和0 eV下的压强曲线:TF结果、TFD结果以及TFK结果比较[19]Fig.3.Pressu re profi le of lead at the temperatu re of 100,10 and 0 eV,the solid,dotted and dashed lines are the resu lts of TF,TFD and TFKmodels,respectively[19].

TFD模型虽然引入了交换修正,但并没有考虑电子的量子效应.1957年,Kirzhnits[20]将电子分布函数展开,在Thomas-Fermi模型中同时引入交换修正和量子修正,形成了Thomas-Fermi-Kirzhnits(TFK)理论.TFK模型引入的修正项和TF模型一样具有普适性,对于TF模型有

TFK模型对TF模型的修正项和TF模型的普适变化关系有所不同,其修正项可以表示为[21]

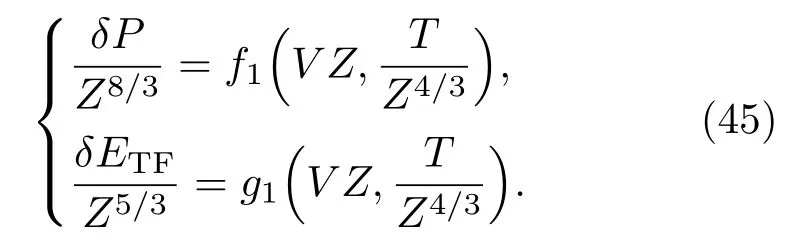
McCarthy[19]详细地列出了较大温度(TZ−4/3)和体积范围内(VZ)压强和能量的计算结果.在计算精度要求不是很高的情况下,TFK方法的解析拟合表达式[12,22]可以为高能量密度条件下的流体模拟提供简单的状态方程.

从图3可以看出,在100 eV的高温时,三种模型(TF,TFD,TFK)基本重合在一起;10 eV时,TF模型结果稍微偏高,但在零温且密度较低时,TF模型压强明显偏大,而TFD模型和TFK模型由于考虑了交换修正以及量子效应修正,比TF模型要精确.

TF模型把所有电子作为准自由电子处理,但实际上靠近原子核的电子受到原子核强烈的Coulomb作用,仍处于束缚态,具有壳层结构.靠近原子核内层电子处于束缚状态,遵从量子力学规律,而较外层的电子由于热电离或者压致电离较容易受激发成为自由电子,因此将原子内的电子分成束缚电子和自由电子两部分来处理更接近实际情况.考虑壳层结构修正的TFS(Thomas-Fermi shell)方法[23]就是基于电子分成两部分的设想而改进的TF模型.

将原子体积分为两个区域:内层靠近原子核是电子密度较高的束缚区域;外层是密度较低的自由电子区域.外层可以采用TF模型方法处理,而内层束缚态可以采用Wenzel-Kramers-Brillouin近似处理.TFL方法把束缚电子看成准自由电子,虽然考虑了内层束缚电子但并不求解薛定谔方程.Zink[23]分别使用TFL(Thomas-Fermi like)方法和TFS方法计算了铁的压强,如图4所示.壳层修正在低温低密度条件下起作用,在高温或者高密度条件下,两者差不多完全重合.在低温低密度时,TFS结果反映了电子的凝聚现象,即∂p/∂ρ较小,因为一些束缚态能级处于空缺状态,外层自由电子较容易重新回到束缚态.当密度增加到一定程度时,束缚态能级充满电子,随着压缩继续进行,将会出现压致电离,这时压强会突然升高.于是,这种电子凝聚和压致电离交替现象发生在TFS结果中.Lee和Thorsos[24]对TFS方法进行了改进,认为有些电子可能处于自由态和束缚态之间的共振状态,将电子分成自由电子以及束缚电子和共振态电子三项,提出了TFSR方法.他们对Z=5到Z=30的各种元素进行了计算,结果如图5[24]所示.可以看出,压强随Z呈现周期性变化,这和TF模型压强随原子序数Z单调上升有明显区别.

图4 铁在7.7和770 eV下,不同密度时的压强,图中分别给出了TF模型、TFL模型以及TFS模型结果[23]Fig.4.Pressure profi le of iron with diff erent density at the temperature of 7.7 and 770 eV,the solid,dashed and dashed-dotted lines are the resu lts of TF,TFL and TFSmodels,respectively[23].

平均原子(average atom,AA)模型[25−27]也可用于高温下计算等离子体中的电子结构.AA模型不区分离子的不同组态,而是把等离子体中所有离子等效成一个平均原子.在这个原子中,电子按照Fermi-Dirac统计规律排布在各个单电子轨道上,忽略了电子之间不同的耦合方式所带来的差异.AA模型电子轨道类似于氢原子轨道,轨道上的电子分布呈现出壳层结构.这是AA模型和TF模型的主要区别,也是其在低温低密度下具有更高精度的原因.AA模型发展至今已有许多改进,比如不可分辨的跃迁系模型[28,29],超级跃迁系模型[30,31],细致谱模型[32]等,这些模型对电子壳层结构考虑得越精细,所计算的状态方程越精确,但所需要的计算量也越大.

图5 不同温度及电子数密度下TF模型和TFSR模型压强和原子序数的关系[24]Fig.5.The relations of pressure and atomic number at d iff erent density and diff erent temperature,the dotted and solid lines are the resultsof TFSR and TFmodels,respectively[24].

5 强耦合等离子体

前面所介绍的模型都是基于单原子假设,即离子之间的相互作用能相对于离子的动能可以忽略不计,物质的性质可简化为求单个原子的性质.当物质处于密度较高,而温度并不是特别高的温稠密或者热稠密状态时,满足ΓD～1或者ΓD≫1,α～1,即离子间的耦合较强,电子处于部分电离部分简并态,这时使用单原子的性质来推导物质的宏观性质将会带来较大误差.

把强耦合等离子体分为电子和离子两部分进行描述.对于电子部分的描述,可以采用TF模型、AA模型、无轨道(orbital-free,OF)模型以及量子力学理论.离子间相互作用可采用超网链(hypernetted-chain,HNC)模型[33−35]、蒙特卡罗(MC)方法以及MD方法进行描述.结合电子的描述模型以及离子相互作用模型,涌现了一大批计算高温稠密物质物态性质的模型方法:Ofer等[36]采用TF模型来描述电子结构,离子间相互作用采用HNC近似来处理.Furukawa和Nishihara[37]采用AA模型并考虑量子修正的 HNC近似处理离子相互作用.Zérah等[38−41]采用TF模型计算电子密度空间分布,采用MD来描述离子间相互作用,提出了TFMD模型.Dharma-wardana和Francois[42]在密度泛函框架下通过Kohn-Sham方程处理电子问题,然后采用HNC近似来描述高温稠密等离子体;Dharma-wardana和Murillo[43]采用双温模型解决高温稠密物质中的离子间相互作用问题.Zérah等[44,45]结合无轨道密度泛函理论和MD方法,发展了无轨道分子动力学方法(OFMD).侯永等[46,47]结合考虑能级展宽效应的AA模型和MD方法提出了AAMD模型.Car和Parrinello[14]结合密度泛函理论和MD方法,提出了第一性原理分子动力学方法(CPMD).Dai等[48−50]基于量子分子动力学方法,考虑了高温下电子碰撞离子对离子位置所形成的涨落,发展了能描述从低温凝聚态到高温理想等离子体的量子Langevin分子动力学方法(QLMD).前面几种基于TF模型、OF模型、AA模型的半经验方法,适用于特定的温度以及密度条件,而基于第一性原理的QMD,以及基于路径积分的蒙特卡罗(PIMC)方法[51]被认为是比较精确的模型.但它们所需计算量非常巨大,尤其是PIMC方法,计算量随着电子个数急剧增加,其应用受限于电子数很少的低Z原子.由于计算量大,QMD方法所能给出的状态方程数据点较少,所以一般被用来作为评判其他半经验方法是否适用的基准[52−54].

随着计算方法和超级计算机的发展,分子动力学方法得到了迅速发展,分子动力学方法可以有效地描述离子之间的相互作用,但前提是需要离子之间相互作用势.下面分别介绍使用经验或者半经验势的经典分子动力学方法和利用量子力学原理直接计算相互作用势的量子分子动力学方法.

5.1 经典分子动力学方法

MD方法是一种用来计算经典多体体系平衡和传递性质的方法,其目的是模拟系统的微观细致动力学行为.在分子动力学方法中,忽略原子核运动的量子效应,原子核的运动满足经典力学的牛顿定律.当体系中所有粒子上的作用力已知时,便可以通过牛顿运动方程得到系统中所有粒子的运动轨迹,再通过统计平均得到该系统的宏观热力学参数.由于粒子在势场中运动,其受力等于势函数的空间导数,因此,从经典力学出发,求解原子间联立牛顿运动方程的分子动力学方法主要包括两个问题:一是粒子相互作用势函数的选取,二是积分牛顿运动方程的求解.

对于一个含有N个粒子的系统,每个粒子的坐标、速度、动量以及受力可以分别表示为ri(t),vi(t),pi(t),f(ri,t),系统的哈密顿量可以表示为

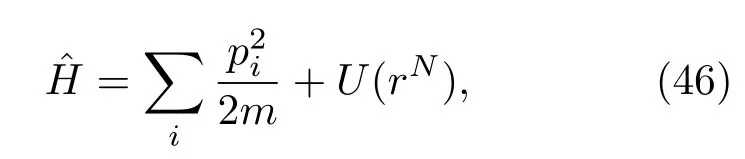
式中第一项是系统动能,第二项U(rN)为系统势能函数,rN=(r1,r2,...,rN)代表N个原子的坐标.哈密顿方程可以表示为

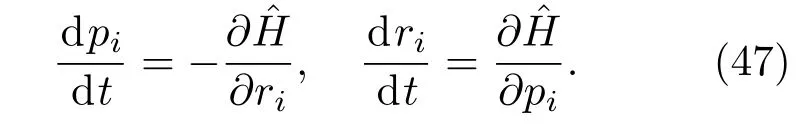
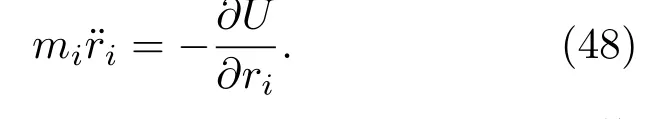
(48)式说明,离子运动所受到的力由离子所处的势场所决定.已知离子所处的势场,通过(48)式加上初始条件以及周期性边界条件,可以进行数值求解,从而得到离子的运动轨迹,进而得到各种宏观物理量.根据统计物理思想,系统经过足够长的时间之后会处于平衡状态,从而表征系统宏观性质的物理量A可以通过时间平均得到

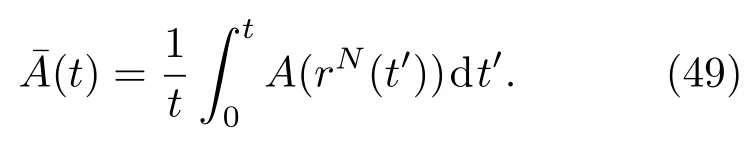
在时间足够长、系统达到平衡态后,有

分子动力学方法的实质是利用计算机对系统中所有粒子的牛顿运动方程进行数值求解,得到粒子坐标、速度等动力学量随时间变化的函数,然后通过统计平均求得表征系统宏观性质的物理量.因此分子动力学计算过程可分为下面三个步骤:首先将牛顿方程进行离散化,求解各个粒子在t+∆t的坐标;接下来是计算不同时刻(t+ ∆t,t+2∆t,...,t+l∆t)的某个物理量A(r1(t+∆t),r2(t+∆t),...,rN(t+∆t));最后对各个物理量求平均值:

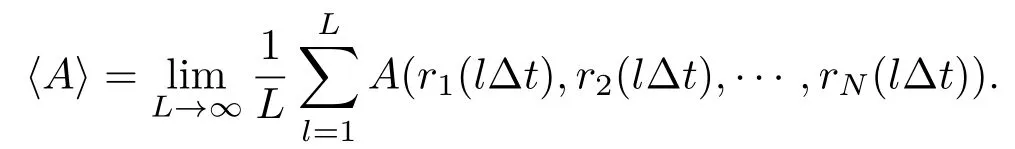
经典分子动力学采用的是经验势或者半经验势,相互作用势不需要另外求解,因此计算速度较快,能够计算的粒子数量也较大,可以达到千万个原子量级.常用的经验势函数有Lennard-Jones势函数[55],Morse势函数[56],Born和Mayer[57]提出的描述离子晶体中离子之间相互作用的Born-Mayer势.至今为止,已经有各种各样的势函数形式被提出,这些势函数只考虑两个原子之间的相互作用,仅和两个原子位置坐标相关,在许多无机化合物中可以有效使用,但对于金属以及共价键结合的有机分子,不能给出精确的结果.在20世纪80年代初,各种考虑了多体相互作用的新势函数被相继提出.Daw和Baskes[58]基于密度泛函理论提出了嵌入原子模型(EAM);Finnis和Sinclair[59]根据密度函数二次矩理论提出了形式上与EAM基本相同的经验F-S模型.Abell[60]在1985年提出了一种Morse形式的多原子间相互作用势模型,比传统的二体势和三体势模型更加精确.

传统势函数对处于常温常压下的物质可以给出很好的描述,而对处于高温等离子体状态时的物质则存在较大误差.一些描述电子结构的半经验方法:比如TF模型、AA模型、OF模型等能够在高温下较精确地描述离子运动的势场.结合这些半经验方法和分子动力学方法便可得到描述高温稠密物质性质的模型:比如TFMD模型[38,41]、AAMD模型[46,47]以及OFMD模型[44,45].但由于TF模型、AA模型以及OF模型的假设都是基于高温的情况,因此这些模型只能在高温下描述电子结构,在低温情况下会带来一定的误差.

5.2 第一性原理分子动力学方法

第一性原理分子动力学方法是基于密度泛函理论计算原子间相互作用势的一种量子分子动力学方法.1985年,Car和Parrinello[14]把密度泛函理论应用到分子动力学中,提出了第一原理分子动力学方法(ab initiomolecular dynamics).该方法极大地推动了计算机模拟低温(T≤10 eV)下物态性质的发展,已成为计算机模拟最先进和最重要的方法之一.由于不需要对离子间势函数做任何经验假设,而是直接采用密度泛函理论求解离子间的相互作用势,因此该方法具有非常强的普适性,并得到了非常广泛的应用[61−67].

在第一性原理分子动力学中,原子核间的相互作用势U(r)由密度泛函理论进行计算,整个分子动力学过程可分为三步:第一步,对于给定的原子核坐标ri,求解Kohn-Sham方程[68]得到粒子数密度分布,进而得到相互作用势;第二步,计算每个原子核受到的力;第三步,求解牛顿运动方程

密度泛函理论基于绝热近似,在求解薛定谔方程时,电子和原子核的坐标同时出现在电子和原子核相互作用项中,直接求解难度非常大.由于原子核质量远大于电子质量,原子核的运动速度相对电子的运动速度非常小.在考虑电子的运动时,可以认为电子绝热于原子核的运动;在考虑原子核运动时,电子可以及时调整空间分布来适应原子核的运动,这就是绝热近似或称Born-Oppenheimer近似[69].通过绝热近似,求解多粒子体系薛定谔方程可以简化为分别求解电子运动和原子核运动的问题.密度泛函理论的基本思想是将原子、分子和固体的基态物理性质用粒子密度函数来描述.密度泛函理论的基础是Hohenberg和Kohn关于非均匀电子气体理论的Hohenberg-Kohn定理[70].粒子数密度函数是确定多粒子系统基态物理性质的基本变量,要确定系统基态物理性质需要三个确定量:粒子数密度函数、动能泛函、交换关联能泛函.粒子数密度函数和动能泛函可以采用Kohn-Sham方程进行求解;而交换关联能泛函一般采用局域密度近似[71]和广义梯度近似[72]得到.

原则上,量子分子动力学方法可以描述任意条件下物质的物态性质,但第一性原理分子动力学的应用范围一直局限于温度较低的区域(10eV以下),主要有以下原因:第一是在高温条件下需要非常大的计算量;第二是大部分第一性原理程序为了减少计算量都是基于赝势实现的,而在高温高压下对赝势的标准和构造要求较高;第三是高温状态难以达到热平衡,计算过程中难以保证收敛性[73].当温度较高时,许多电子成为非局域电子或自由电子,相对于离子运动的时间尺度,电子运动的时间尺度非常小,因此在每一分子动力学时间步中电子与离子发生了多次碰撞.在温度升高时,自由电子增多,电子的运动速度增快,与离子碰撞次数也增多,这时碰撞引起离子位置的涨落是不可忽略的,Born-Oppenheimer近似也不再成立.传统的第一性原理分子动力学方法基于Born-Oppenheimer近似,并没有考虑离子位置的涨落,因此在高温下的计算不可避免地带来一些问题.Dai等[48−50]对电子与离子在高温下的碰撞作用采用类似布朗运动的思想来处理,引入离子-电子碰撞项,利用Langevin方程描述离子运动,取得了很好的效果,并将第一性原理分子动力学方法拓展到了理想等离子体、高能量密度物理区域,填补了低温凝聚态与高温稠密状态之间的空白.

第一性原理分子动力学方法和其改进方法虽然能够在很大密度以及温度范围内精确地得到物质的状态参数,但由于其计算的复杂性以及所耗计算机时巨大,在精确度要求不是特别高的流体模拟中不如一些经验或者半经验的模型简单方便.一些全局状态方程就是在不同温度密度区域结合各类实验结果、理论结果再采用插值方法获得的,比如More等[74]所提出的QEOS(quotidian equation of state),以及美国洛斯阿拉莫斯国家实验室的SESAME数据库[75].

5.3 全局状态方程

高能量密度条件下的流体动力学过程涉及非常宽泛的物态范围,比如惯性约束聚变中所涉及的温度范围为10−3—104eV、密度范围为10−3—102g/cm3,因此在流体动力学模拟中需要全局状态方程.全局状态方程就是在非常大的密度和温度范围内描述压强P(ρ,T)和内能E(ρ,T).尽管量子分子动力学方法原则上可以对任意状态的物质提供统一的描述,但实际上,目前还没有哪个模型能够覆盖所有区域和所有物质,从而不能满足流体动力学模拟的需求.在不同区域采用不同的近似模型,并在这些区域间进行光滑的插值,从而构筑全局状态方程模型是目前所采用的主要方法.目前已有一些大范围的状态方程(EOS)模型,比如Bushman和Fortov[76],Godval和Sikka[77],Basko[78]所提出的各种模型以及More等[74]所提出的QEOS模型.还有一些是以表格形式给出的,比如SESAME数据库[75].SESAME数据库的状态方程数据是在不同温度密度区域结合各类实验、理论结果采用插值方法获得的.SESAME数据库和QEOS模型使用比较广泛,它们也是很多文献进行状态方程数据分析和比对的重要参考.

QEOS把自由能分为电子项、离子项以及半经验的束缚修正项,表示如下:

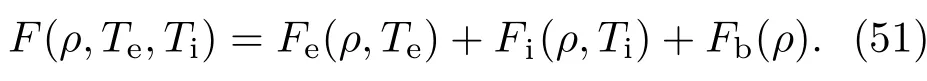
对于电子项的贡献Fe,可采用TF模型进行计算;对于离子项的贡献Fi,在固体中把热离子当作声子气体处理,采用玻色-爱因斯坦统计进行计算,流体中则采用Cowan模型处理.半经验的束缚项自由能不依赖于温度,可表示为

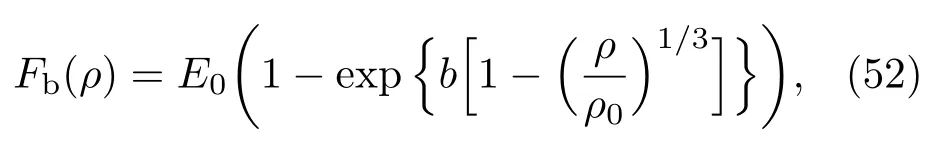
式中E0和b是两个经验参数,它们满足以下两个关系式:第一个是在常温和固体密度条件下,总压强为0;第二个是需要知道物质的体积模量以及物质的初始密度,通过压强和自由能的热力学关系式再联立(51)式可以得到压强和两个经验参数的关系,再通过B=ρ0(∂P/∂ρ)ρ0在已知体积模量B以及初始密度ρ0的条件下可以得到另一个关于E0和b的关系式.利用这两个关系式可求得两个经验参数E0和b的值.

QEOS模型在国际上得到了比较广泛的使用,很多辐射流体力学程序使用QEOS模型的计算结果作为状态方程参数,QEOS有可以免费获得的计算程序[79].Atzeni和Meyer-ter-Vehn[80]将铝的Hugoniot曲线的理论计算结果与实验结果进行了比较,如图6所示.可以看出,QEOS结果和SESAME结果在104GPa以下与实验所得到的数据[81−84]比较接近.在104GPa以上时,两者之间有一定的差别,但总体上和实验数据符合较好,这说明QEOS和SESAME都能给出较精确的状态方程参数.

图6 铝的Hugoniot曲线[80],图中给出了QEOS结果[74],SESAME结果[75]以及一些实验结果[81−84]Fig.6.Hugoniot curves of aluminum[80],the b lack solid line and red dashed line are the resu lts of QEOS and SESAME,respectively.The dots in figure are experimental resu lts[81−84].

图7[85]给出了温度为5和30 eV时不同密度下Al等离子体的状态方程.图中比较了TF模型[86],QEOS模型[74],SESAME数据库[75],NPA模型[87]以及AAMD模型[88]结果.NPA(neutral pseudoatom)模型[87]采用密度泛函理论处理电子结构,采用HNC近似描述离子间相互作用.从图7可以看出,30 eV时所有模型结果的符合度比5 eV时好.温度较高时,一些基于高温条件的半经验模型,比如TF模型以及AAMD模型,也可以得到比较精确的结果.从图7还可以看出,在5 eV时TF模型以及AAMD模型所得到的结果在较高密度条件下明显要比NPA模型结果、QMD结果以及SESAME数据库结果高.

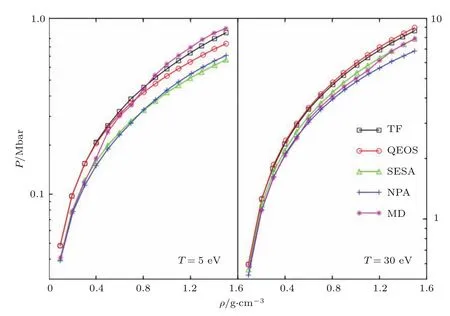
图7 温度为5和30 eV时不同密度下铝的状态方程[85],图中分别是TF模型[86]、QEOS[74]、SESAME[75]、NPA模型[87]以及AAMD模型[88]的计算结果比较Fig.7.The EOS of aluminiumunder the temperatu re of 5 and 30 eV[85],the solid lineswith d iff erentmarks are the resu lts of TF[86],QEOS[74],SESAME[75],NPA[87]and AAMD[88]models.

图8[89]给出了TFMD模型[90]、 OFMD模型[73]、AAMD模型[88]、QMD模型、QLMD模型[50]以及SESAME数据库[75]在不同温度下铁的Hugoniot曲线.由于高温下QMD模型不容易收敛,因此没有给出高温下QMD的结果.从图8可以看出,在高温段(100 eV以上),TFMD,AAMD,OFMD以及QLMD四个模型和SESAME数据库符合得非常好,这说明四个MD模型在高温下都能较精确地给出铁的状态方程,但在低温下,TFMD模型和OFMD模型结果明显要比其他几个模型要高.相对前两个模型,AAMD模型能在更低的温度下给出精确结果.这三种半经验模型结果在低温下比量子分子动力学结果要高,这说明了低温下使用半经验模型的局限性.温度较低时,电子交换、关联作用需要考虑[91],而TFMD方法在计算电子压强时没有考虑交换、关联作用所产生的负压强对总压强的贡献,所以TFMD在低温区给出的压强偏高.AA模型虽然考虑了电子的壳层结构,但也只是简单的结构近似,因此低温时AAMD的精确度也会下降,这时只有基于密度泛函理论的量子分子动力学模型才能给出较精确的结果.在0.1 eV的低温下,电子的自旋效应不能被忽视,考虑了量子自旋效应的QLMD模型结果比未考虑量子自旋效应的结果要稍微高一些,与SESAME数据库结果更接近.

图8 不同温度下铁的Hugoniot曲线[89],图中分别给出了考虑了交换作用的TFMD模型[90]、AAMD模型[88]、OFMD模型[73]、QMD模型以及QLMD[50]结果和SESAME数据库[75]结果Fig.8.The Hugoniot cu rve of iron at diff erent temperatu res[89],the resu lts of TFMD[90],AAMD[88],OFMD[73],QMD,QLMD[50]and SESAME[75]models are presented,respectively.

图9[89]针对铁的Hugoniot曲线给出了TFD模型[90]、VAAQP模型[92](variational-averageatom-in-quantum-plasmas,基于平均原子模型近似)、QEOS模型、QLMD模型[50]以及SESAME数据库和各种实验结果[81,93,94]的比对.由于冲击压缩实验中一些物理量的测量比较困难,实验结果有较大的不确定性,因此各类实验点的数据比较分散.从图9可以看出,不同的理论模型给出的结果也存在一定差异,尤其压强在10 Mbar以下、固体密度在2.5倍以下的温稠密物质区域,差别非常明显.在此区域,TFD模型以及VAAQP模型结果偏大.QEOS模型、QLMD模型以及SESAME数据库结果与俄罗斯的Rusbank数据库[93]的结果十分接近.在高压高密度情况下,各种模型虽然有一定的差异,但总体而言与实验结果符合较好.这说明在高温情况下,各种半经验的统计模型也能给出比较精确的结果.

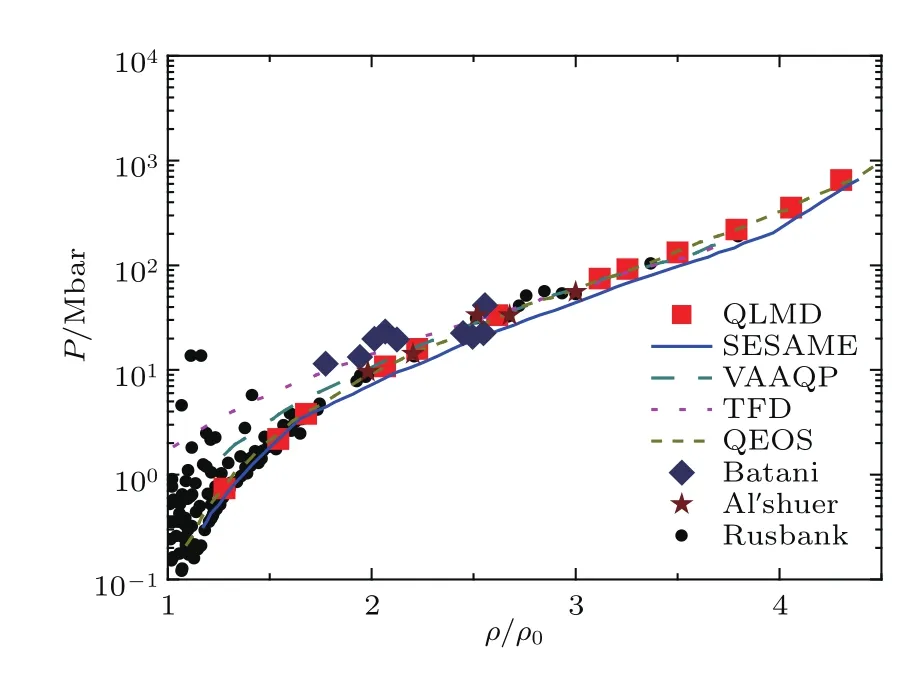
图9 铁的Hugoniot线的实验和理论结果的对比[89]Fig.9.The Hugoniot cu rve of iron[89],the lines are the resu lts of various theoreticalmodels and the dots are the experimental results.

6 结 语

本文根据离子耦合系数以及电子简并度参数在温度密度平面内把等离子体状态划分为四个区域,对四个区域内等离子体的状态方程及其热力学性质进行了简要总结.在完全电离等离子体区域,温度非常高,原子完全电离,粒子之间相互作用非常小,电子和离子都可以采用理想气体状态方程描述.在部分电离弱耦合等离子体区域,部分电子电离,粒子之间相互作用相对较小,状态方程可以采用Saha方程求解,考虑粒子之间长程Coulomb相互作用后可采用Debye-Hückel方程得到.在强简并等离子体区域,原子核之间的相互作用由于周围电子的屏蔽可以忽略,原子核可采用理想气体状态方程描述,电子采用TF模型可以得到较精确的结果,一些改进型的TF模型可以把TF模型拓宽到更低温度和更低密度.在强耦合等离子体区域,温度不是很高,密度在物质固体密度附近,此时物质处于温稠或者热稠等离子体区域.当等离子体处于前面三个区域时,都有较准确的方法描述等离子体的状态方程,但等离子体处于温稠以及热稠区域时,还没有较完善的理论进行统一的描述.量子分子动力学虽然原则上能够统一描述此区域物质的性质,但由于计算量大、高温不收敛等缺点,其使用也受到一定的限制.一些改进的量子分子动力学方法比如QLMD,虽然明显拓宽了量子分子动力学方法的使用范围,但其使用条件以及准确性仍需要进一步验证确认,而且其计算量过大,需要经过大量的计算和累计才能得到较密集的状态方程插值表,以满足流体动力学过程模拟的需要.一些半经验分子动力学方法,比如TFMD,AAMD,OFMD等,计算量虽小,但在低温下的计算结果误差较大.可见,发展描述温稠和热稠区域的先进理论模型十分必要.另一方面，流体动力学模拟所使用的状态方程需要兼顾计算量和精度.状态方程计算方法过于复杂,计算量太大,满足不了流体动力学模拟的需要;而状态方程参数精确度太低,也会对流体动力学模拟结果的可靠性产生较大影响.因此,采用不同的简单模型在不同密度和温度区域进行插值,不失为一种快速获得等离子体状态方程的好方法.

[1]Fortov V E 2016Extreme States of Matter(Berlin:Springer)p9

[2]Xu J A,MaoHK,Bell P M1986Science232 1404

[3]Ming L C,BassettW A1974Rev.Sci.Instrum.45 1115

[4]NellisW J 2006Rep.Prog.Phys.69 1479

[5]Q ian X S 2007Lectures on Physics(Shanghai:Shanghai Jiaotong University Press)(in Chinese)[钱学森2007物理力学讲义(上海:上海交通大学出版社)]

[6]Fortov V E 2007Phys.Uspek.50 333

[7]Lind l J D,Amend t P,Berger R L,G lendinning S G,G lenzer S H,Haan SW,Kau ffman R L,Landen OL,Su ter L J 2004Phys.P lasmas11 339

[8]Saha MN,Srivastava BN 1965ATreatise on Heat(Allahabad:The India Press)

[9]Debye P,Hückel E 1923Physik Z24 185

[10]Thomas L H1927Proc.Cambridge Philos.Soc.23 542

[11]Fermi E 1928Z.Phys.48 73

[12]Xu X S,Zhang W X 1986Theory Guide of Practica l Equations of State(Beijing:Science Press)(in Chinese)[徐锡申,张万箱 1986实用物态方程理论导引(北京:科学出版社)]

[13]Feynman R P,Metropolis N,Teller E 1949Phys.Rev.75 1561

[14]Car R,ParrinelloM1985Phys.Rev.Lett.55 2471

[15]Letter R 1955Phys.Rev.99 1854

[16]D irac P AM1930Proc.Camb.Phil.Soc.26 376

[17]Cowan R D,Ashkin J 1957Phys.Rev.105 144

[18]Bloch F 1929Zeits.F Phys.57 545

[19]McCarthy S L 1965Lawrence Livermore Laboratory ReportUCRL-14364

[20]Kirzhnits D A1957Sov.Phys.JETP5 64

[21]Tang W H,Zhang R Q 2008In troduction tothe Theory and Compution of Equations of State(Beijing:Higher Education Press)(in Chinese)[汤文辉,张若棋2008物态方程理论及计算概论(北京:高等教育出版社)]

[22]Bell AR 1980Rutherford and Appleton Laboratories ReportRL-80-091

[23]Zink JW 1968Phys.Rev.176 279

[24]Lee C M,Thorsos BI1978Phys.Rev.A17 2073

[25]Rozsnyai BF 1972Phys.Rev.A5 1137

[26]Rozsnyai BF 1982J.Quan t.Spectrosc.Radiat.Transf.27 211

[27]Rozsnyai BF,Lamou reux M1990J.Quan t.Spectrosc.Radiat.Transf.43 381

[28]Bauche-Arnou lt C,Bauche J,Klapisch 1978M.J.Opt.Soc.Am.68 1136

[29]Bauche-Arnou lt C,Bauche J,Klapisch M1979Phys.Rew.A20 2424

[30]Bar-ShalomA,Oreg J,Goldstein W H,Shvart D,Zigler A1989Phys.Rev.A40 3183

[31]Oreg J,Goldstein W H,Bar-ShalomA,Klapisch M1990J.Comput.Phys.91 460

[32]Iglesias C A,Rogers F J,W ilson BG 1987Astrophys.J.322 45

[33]Kurten KE,Ristig ML,Clark JW 1977Lett.Al NuovoCimen to20 313

[34]Kang HS,Ree F H1998Phys.Rev.E57 5988

[35]Rose D V,GenoniTC,W elch D R,C lark R E,Campbell R B,Meh lhorn TA,Flicker D G 2009Phys.P lasams16 102105

[36]D ror O,Nard i E,Rosen feld Y 1988Phys.Rev.A38 5801

[37]Fu rukawa H,N ishihara K1992Phys.Rev.A46 6596

[38]Zérah G,C lérouin J G,Pollock E L 1992Phys.Rev.Lett.69 446

[39]C lérouin J G,Pollock E L,Zérah G 1992Phys.Rev.A46 5130

[40]Flavien L,Gilles Z 2006Phys.Rev.E73 016403

[41]Danel J F,Kazand jian L,Zérah G 2006Phys.P lasmas13 092701

[42]Dharma-wardana MW C,Francois P 1982Phys.Rev.A26 2096

[43]Dharma-wardana MW C,MurilloMS 2008Phys.Rev.E77 026401

[44]Danel J F,Kazand jian L,Zérah G 2009Phys.Rev.E79 066408

[45]Horner D A,Lambert F,Kress J D,Collins L A2009Phys.Rev.B80 024305

[46]Hou Y,Jin F T,Yuan J M2006Phys.P lasmas13 093301

[47]Hou Y,Jin F T,Yuan J M2007J Phys.:Condens.Matter19 425204

[48]Dai J,Yuan J 2009Europhys.Lett.88 20001

[49]Dai J,Hou Y,Yuan J 2010Phys.Rev.Lett.104 245001

[50]Dai J,Hou Y,Yuan J 2010Astrophys.J.721 1158

[51]Militzer B2009Phys.Rev.B79 155105

[52]W unsch K,Vorberger J,Gericke D O2009Phys.Rev.E79 010201

[53]Gericke D O,W unsch K,G rinenkoA,Vorberger J 2010J.Phys.:Conf.Ser.220 012001

[54]Pey russe O,Mazevet S,Recou les V,Dorchies F,Harmand M,Levy A,Fuchs J,Mancic A,NakatsutsumiM,Renaudin P,Audebert P 2009CP,Atomic Processes in P lasmas1161 200

[55]Frenkel D,Smit B1996Understanding Molecular Simu lation(San D iego:Acedemic Press)

[56]Morse P M1929Phys.Rev.34 57

[57]Born M,Mayer J E 1931Z.Phys.75 1

[58]DawMS,Baskes MI1983Phys.Rev.Lett.50 1285

[59]Finnis MW,Sinclair J E 1984Philosophic Magazine A50 45

[60]Abell G C 1985Phys.Rev.B31 6184

[61]Collins L,Kwon I,Kress J,Trou llier N,Lynch D 1995Phys.Rev.E52 6202

[62]Desjarlais MP,Kress J D,Collins L A2002Phys.Rev.E66 025401

[63]Mazevet S,C lérouin J,Recou les V,Anglade P M,Zérah G 2005Phys.Rev.Lett.95 085002

[64]Mazevet S,Desjarlais MP,Collins L A,Kress D,Magee N H2005Phys.Rev.E71 016409

[65]C lérouin J,Noiret P 2008Phys.Rev.B78 224203

[66]Holst B,Redmer R 2008Phys.Rev.B77 184201

[67]Mazevet S,Zérah G 2008Phys.Rev.Lett.101 155001

[68]Kohn K,ShamL J 1965Phys.Rev.140 A1133

[69]Born M,Huang K1954Dynamical Theory of Crystal Lattice(Ox ford:Ox ford University Press)

[70]Hohenberg P,Kohn W 1964Phys.Rev.B136 864

[71]Hansen J P,McDonald IR 1976Theory of Simple Liquids(Lodon:Academic Press)

[72]PerdewJ P,Kieron B,Matthias E 1996Phys.Rev.Lett.77 3865

[73]Lambert F,Clérouin J,Zérah G 2006Phys.Rev.E73 016403

[74]More R M,W arren KH,Young D A,Zimmerman G B1988Phys.F luids31 3059

[75]Lyon S P,Johnson J D 1992SESAME:The Los Alamos National Laboratory Equation of State DatabaseReport No.LA-UR-92-3407

[76]Bushman AV,Fortov V E 1983Soviet Phys.Uspek.26 465

[77]Godval BK,Sikka S K1983Phys.Rep.102 121

[78]BaskoMM.Metallic 1985Soviet High Temperat.Phys.23 388

[79]KempAJ,Meyer-ter-Vehn J 1998Nucl.Instrum.Meth.Phys.Res.A415 674

[80]Atzeni S,Meyer-ter-Vehn J 2004The Physics of Inertia l Fusion(NewYork:Oxford University Press)

[81]Altshu ler L 1965Soviet Phys.Uspek.8 52

[82]Ragan C E 1982Phys.Rev.A25 3360

[83]V lad imirov AS,Voloshin N P,Nogin V N,Petrov tsev AV,SimonenkoV A1984JETP Lett.39 82

[84]Mitchell AC,Nellis W J 1981J.Appl.Phys.52 3363

[85]Hou Y 2009Ph.D.D issertation(Changsha:National University of Defence Technology)(in Chinese)[侯永2009博士学位论文(长沙:国防科学技术大学)]

[86]Letter R 1955Phys.Rev.99 1854

[87]Perrot F,Dharma-wardana MW C,Benage J 2002Phys.Rew.E65 046414

[88]Hou Y,Yuan J 2009Phys.Rev.E79 016402

[89]Dai J Y 2009Ph.D.D issertation(Changsha:National University of Defence Technology)(in Chinese)[戴佳钰2010博士学位论文(长沙:国防科学技术大学)]

[90]Lambert F,C lérouin J,Mazevet S 2006Europhys.Lett.75 681

[91]Fromy P,Deu tsh C,Maynard G 1996Phys.P lasmas3 714

[92]Piron R,Blenski T2011Phys.Rev.E83 026403

[93]Shock W ave Database http://www.ihed.ras.ru/rusbank/gassim/[2003-07-13]

[94]Batani D,Morelli A,Tomasini M,Benuzzi-Mounaix A,Philippe F,Koenig M,Marchet B,Masclet I,Rabec M,Reverd in C,Caub le R,Celliers P,Collins G,Silva L D,Hall T,Moret M,Sacchi B,Baclet P,Cathala B2002Phys.Rev.Lett.88 235502

PACS:05.70.Ce,52.25.KnDOI:10.7498/aps.66.030505

Equations of state and thermodynamic properties of hot plasma

Tang Wen-Hui†Xu Bin-Bin Ran Xian-Wen Xu Zhi-Hong

(College of Science,National University of Defense Technology,Changsha 410073,China)(Received 17 October 2016;revised manuscript received 17 December 2016)

The equations of state(EOS)and the thermodynamics properties of plasma under high temperature are widely applied tothe fields of astrophysics,controllable fusion,weapon design and damage.In this paper wemain ly reviewthe theoreticalmodel and computing method of the EOS of hot plasma on diff erent density scales and temperature scales.For an ideal plasma,the interaction between ions can be ignored,the EOS is simple and the theories turn matured.Under the condition of extremely high temperature,ions are ionized completely and the EOSs of ions and electrons can be approximated by the EOS of ideal gas.W hen the temperature is not very high and ions are just partly ionized,the EOS can be obtained by Saha model or its modified model.W hen atoms are strongly compressed,the EOS can be calculated by Thomas-Fermimodel or its modified model.For the non-ideal plasma,there is a strong coupling between ions.Nounified theoreticalmodel can completely describe the interaction between ions at arbitrary density and arbitrary temperature.In principle,the quantummolecular dynamics(QMD)can accurately describe the EOS of plasma in large density range and large temperature range.However,due tothe enormous computation and the diffi culty in converging,it is diffi cult toapply QMD tothe plasma under high temperature.W ith simple computing method and small computation,classicalmolecu lar dynamics using semi-empirical potential can calcu late the EOS accurately at high temperature.However,it will produce great error at lower temperature.It is a simple and eff ective way toobtain a global EOS by using diff erent theoreticalmodels in diff erent density range and diff erent temperature range and by interpolating in the vacant density range and vacant temperature range.

hot plasma,equations of state,thermodynamics properties

10.7498/aps.66.030505

†通信作者.E-mail:wenhuitang@163.com

†Corresponding author.E-mail:wenhuitang@163.com