动态环路法磁矩测量技术试验研究
2016-10-17刘超波孟立飞代佳龙
刘超波,王 斌,易 忠,孟立飞,肖 琦,代佳龙
(北京卫星环境工程研究所,北京100094)
动态环路法磁矩测量技术试验研究
刘超波,王斌,易忠,孟立飞,肖琦,代佳龙
(北京卫星环境工程研究所,北京100094)
动态环路法磁矩测量技术是一种新的磁矩测量技术,为了解其实际性能指标,提出一种可以获得动态环路法测量误差和分辨率的测试方案。利用标准磁体模拟被测物,通过改变标准磁体的位置模拟被测物在任意方向的偏心情况,给出9组被测标准磁体设计方案。通过对比不同标准磁体的磁矩测量结果,得到原理样机在一定误差条件下的磁矩分辨率,并给出提高分辨率的方法。试验结果表明:动态环路法原理样机偶极磁矩测量误差<5%,磁心坐标测量误差<20%;在偶极磁矩测量误差<5%时,原理样机的磁矩分辨率可达0.06A·m2。动态环路法具有良好的性能指标,可以用于高精度磁矩测量。
磁矩;动态环路法;误差;分辨率
0 引 言
随着航天器长寿命、高可靠要求的提高,空间磁环境效应研究的重要性日显突出[1-2]。在航天器发射前,需要在地面完成航天器整星或部组件磁试验,以控制或利用航天器磁性,而磁矩测量是航天器磁试验的重要组成部分[3-4]。为了确保航天器在轨可靠运行,需要磁矩测量方法具有很高的测量准确度和可靠性。
动态环路法是一种新的磁矩测量方法,该方法利用偏心偶极子模型等效被测物体的磁性,能够测得物体的偶极磁矩分量和四极磁矩分量,并能够通过公式计算出物体的磁心坐标[5]。目前,动态环路法磁矩测量原理研究已经完成,但是其工程可行性和可靠性还有待验证。为验证和了解动态环路法磁矩测量技术的可行性和可靠性,获得其测量误差、分辨率等参数,本文首先对动态环路法原理样机的磁矩和磁心坐标测量误差进行了测量和分析,然后对原理样机的分辨率进行了分析。
1 动态环路法简介
动态环路法通过测量物体从5组特殊构造感应线圈中直线通过时产生的一系列磁通量,利用反演公式计算出物体的磁矩值,包括3个方向的偶极磁矩(Mg10、Mg11、Mh11)和5个等效四极磁矩(Mg20、Mg21、Mh21、Mg22、Mh22),进而还可以计算出物体的磁心坐标[6]。自研动态环路法磁矩测量技术原理样机中磁通感应线圈的直径为1.5m,物体可直线移动距离为7m,所使用的磁通计分辨率为0.1μWb。
2 误差测量方案
2.1方案设计原则
动态环路法的一个重要特点就是能够获得被测物体的磁心坐标位置,因此在误差测量方案中需要让被测物体处于偏心位置,不能处于线圈中心点(坐标系原点)。同时,考虑到同一个磁体在不同偏心距离的测量误差可能会不一样,所以需要设置不同的偏心距离。另外,测量方案需要考虑被测磁体的个数,以考察原理样机对单个或多个磁体的测量效果。
2.2偏心单个磁矩测量方案
对于单个偶极磁体,磁体的位置坐标就是磁心坐标,共有9种偏心情况:1)x方向磁矩分量(Mg10)分别向x、y、z方向偏心;2)y方向磁矩分量(Mg11)分别向x、y、z方向偏心;3)z方向磁矩分量(Mh11)分别向x、y、z方向偏心。
由动态环路法测量原理[3]可知,对于x方向的磁矩分量,y向偏心和z向偏心是对称的,同时,又因为h分量和g分量的一一对应关系,所以在上述9种测量方案中,只有5种独立情况。以此建立5种偏心单个磁矩设计方案,如图1所示,图中M为标准偶极磁体,大小为2.8A·m2,箭头代表磁矩方向。

图1 5种偏心单个磁体示意图
5组方案中向x、y、z 3个方向的偏心距离设计为8,16,24,32,40,48,56cm 7个不同值,此范围基本涵盖了原理样机所能测试件的最大偏心值。只有一个偶极磁体时,其位置坐标即为磁心坐标[7]。
2.3组合磁矩测量方案
对于被测磁体中包含多个偶极磁矩的情况,被测磁体的偶极磁矩大小应是其所包含的所有偶极磁矩的矢量和,其磁心位置也应该符合磁心公式的计算结果[8-9]。此处只考虑两个偶极磁矩的情况,多于两个偶极磁矩的组合磁体可以以此累加。两个偶极磁矩的典型组合方式有以下4种(不用考虑z方向):
1)两个处于x方向不同位置的磁矩分量;2)两个处于y方向不同位置的磁矩分量;3)y方向磁矩处于原点,x方向磁矩在y方向偏心;4)x方向磁矩处于原点,y方向磁矩在x方向偏心。
按照上述4种组合方式,将标准偶极磁体M1和M2分别按照图2所示的位置摆放,建立4种组合磁体设计方案,其中M1和M2的大小均为1.4A·m2,箭头方向代表磁矩方向。表1为4种组合磁体设计方案的各分量磁矩大小及磁心坐标设计值。

图2 组合磁体设计示意图
3 测量结果
3.1偏心单个磁体测量结果
图3为5种方案的测量结果误差曲线图。从图3(a)中可以看出,磁矩Mg10随着磁心在x方向的偏心值增加,误差呈现单方向增加趋势,在偏心距离≤56cm时,其误差均≤3%。磁心坐标Xm的误差随着磁心位置的变化而变化,随着偏心距离的增加,误差变化较大,最大误差<12%。因为Xm是Mg20与Mg10的比值,而Mg10的变化量较小,所以误差主要是由Mg20分量的测量误差所带来的。另外,当Xm为16 cm和24cm时,磁心误差虽>10%,但是它的绝对距离偏差值较小。

表1 4组方案的磁矩大小及磁心坐标设计值
从图3(b)中可以看出,磁矩Mg10的误差随着磁心在y方向偏心距离的增加而不断增大,在偏心距离Ym≤56cm时,磁矩的误差均<5%,Ym的测量误差在2%~7%之间波动。
从图3(c)中可以看出,磁矩Mg11的测量误差保持在0.2%左右,与其在x方向上的位置基本无关,这是因为测量过程中Mg11产生的一系列磁通量沿x方向的积分结果不变,与动态环路法测量理论相符。Xm的误差最大不超过9%,且随着偏心距离的变化而剧烈变化,由于Xm是Mg21与Mg11的比值,而Mg11基本不变,所以误差主要是由于Mg21分量的测量误差引起的。
从图3(d)中可以看出,磁矩Mg11的测量误差随着磁心位置在y方向的变化在±4%内波动,Ym的测量误差则比较复杂,在±20%之间变化。
从图3(e)中可以看出,对于Mg11分量,当磁心坐标Zm不同时,磁矩分量Mg11的测量误差均在-4%左右,测量结果较稳定,说明磁矩测量误差主要是系统误差。Zm的测量误差除了前两个值之外都<5%,Zm为8cm和16cm时,误差虽然较大,但Zm的绝对偏差很小。

图3 5种偏心单个磁矩方案的测量结果误差
3.2组合磁体测量结果
4种组合磁体的磁矩大小及磁心坐标测量结果及误差见表2。
由表2可以看出,偶极磁矩的测量误差均<5%,四极磁矩的测量误差则有时会比较大,这也导致了磁心测量结果的误差偏大,磁心测量误差≤8.8%。
4 原理样机偶极磁矩分辨率
4.1偶极磁矩分辨率分析
为了得到原理样机的偶极磁矩分辨率,利用原理样机对一组磁矩值处于0.05~0.45A·m2之间的标准磁体进行了测量,测量结果见图4。
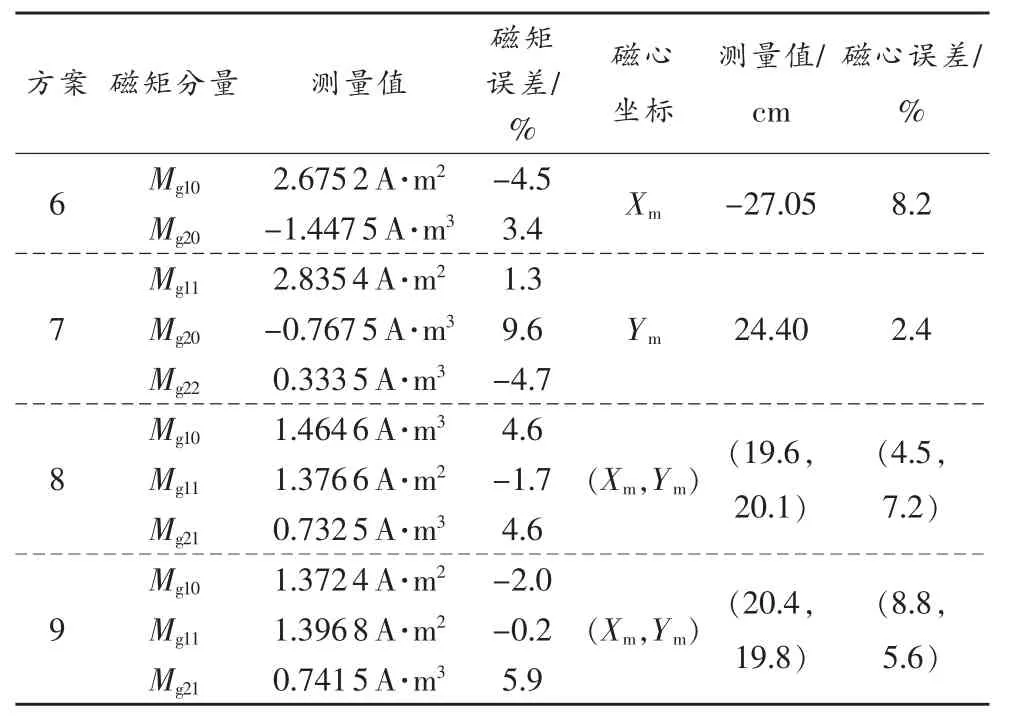
表2 4组组合磁体的测量结果及误差

图4 分辨率测量结果误差曲线
可以看出,在被测磁体磁矩>0.15A·m2时,原理样机的测量误差均≤2.5%;当磁矩<0.15A·m2时,测量误差随着被测磁体磁矩的减小而显著增加。误差增大的原因主要是由于磁矩值的减小,使得感应线圈中磁通量减小,由于磁通计分辨率固定,当磁通量小于一定程度时,磁通量的误差会增大,进而使得磁矩计算结果误差增大。根据图4,可以认为在要求原理样机测量误差<5%时,原理样机的分辨率≥0.06A·m2。
4.2提高分辨率的方法
由动态环路法的计算公式[3]可以看出,被测磁矩与感应线圈中的磁通量成正比,也即磁通量的测量准确度越高,得到的磁矩测量值就越准确,相应的原理样机的分辨率就越高,所以要提高原理样机分辨率,就必须提高磁通量的测量准确度。
提高磁通量测量准确度的方法有两个:1)直接提高磁通计的分辨率;2)增加原理样机线圈匝数,以提高磁通量的相对准确度。
5 结束语
本文针对动态环路法磁矩测量技术应用性能的测试需要,在现有原理样机基础上依据动态环路法的测量特点,提出了一种获得原理样机测量误差和磁矩分辨率的方法,并以此对动态环路法磁矩测量技术的实际应用性能进行了测试。
从试验结果可以看出,不管是单个偏心偶极磁体,还是多个偶极磁体的组合,动态环路法原理样机的偶极磁矩测量误差均<5%,这表明动态环路法具有非常高的磁矩测量准确度。同时,磁心测量误差均<20%也表明动态环路法原理样机能够对被测物体的磁心进行比较准确的定位,这对于航天器或潜艇等设备的高准确度磁补偿具有重要的应用价值。在偶极磁矩测量误差<5%时,磁矩分辨率≥0.06A· m2,这也表明动态环路法原理样机具有良好的小磁矩分辨能力。
通过本文的研究,证明了动态环路法磁矩测量技术的可行性和可靠性,为未来动态环路法磁矩测量设备的研制和应用奠定了工程基础。
[1]齐燕文.空间磁环境模拟技术[J].航天器环境工程,2005,22(1):19-21.
[2]NARVAEZ P.The magnetostatic cleanliness program for the Cassini spacecraft[J].Space Science Reviews,2004,114(1/4):385-394.
[3]陈斯文,黄源高,李文曾.双星星上部件磁测及磁测设备[J].地球物理进展,2004,19(4):893-897.
[4]陈俊杰,易忠,孟立飞,等.基于欧拉方法的多磁偶极子分辨技术[J].航天器环境工程,2013,30(4):401-406.
[5]KILDISHEV A V,NYENHUIS J A,BOYKO D L.Applicationof magnetic signature processing to magnetic center pinpointing in marine vehicles[C]∥OCEANS’99 MTS/IEEE Ukraine,1999:1534-1535.
[6]刘超波,易忠,肖琦.动态环路法磁矩测量技术研究[J].航天器环境工程,2012,29(1):55-60.
[7]TIKHONOV A A,PETROV K G.Multipole models of the earth’s magnetic field[J].Cosmic Research,2002,40(3):203-212.
[8]刘超波,王斌,陈金刚,等.磁场全张量测量计算方法与误差分析[J].航天器环境工程,2015,32(1):63-66.
[9]LADYNIN A V,POPOVA A A.Optimization fitting of the eccentric dipole models to the observed geomagnetic field[J].Russian Geology and Geophysics,2009:195-205.
(编辑:李刚)
Experimental study on dynamic loop method for magnetic moment measurement
LIU Chaobo,WANG Bin,YI Zhong,MENG Lifei,XIAO Qi,DAI Jialong
(Beijing Institute of Spacecraft Environment Engineering,Beijing 100094,China)
Dynamic loop method is one of the newest magnetic moment measuring techniques and its performance has not been precisely evaluated yet.A testing scheme is designed to assess the measuring errors and resolutions of this method.That is,standard magnets are assembled into nine simulators of different frameworks to simulate the off-centered dipoles of the measured objects in any direction.The magnetic moments of these simulators are measured by the dynamic loop method and then compared with the results calculated by electromagnetism theory.The results show that the measuring error in the magnetic moment of prototype dipoles is lower than 5%and that of magnetic center coordinates is no more than 20%.When the measuring error of dipole magnetic moment is within 5%,the resolution is as high as 0.06 A·m2.This suggests the dynamic loop method has sound performance indexes and can be applied in high-precision magnetic moment measurement.
magnetic moment;dynamic loop method;error;resolution
A
1674-5124(2016)03-0017-04
10.11857/j.issn.1674-5124.2016.03.004
2015-07-18;
2015-09-03
国家自然科学基金项目(51207011)
刘超波(1987-),男,山东荷泽市人,工程师,硕士,主要从事航天器磁性设计、测量及控制研究。
