单轴压缩下固态硝基苯的第一性原理研究∗

范俊宇郑朝阳苏艳†赵纪军

1)(大连理工大学,三束材料改性教育部重点实验室,大连 116024)2)(中国工程物理研究院流体物理研究所,冲击波与爆轰物理国家实验室,绵阳 621900)(2016年10月9日收到;2016年11月21日收到修改稿)

专题:高压下物质的新结构与新性质研究进展

单轴压缩下固态硝基苯的第一性原理研究∗

范俊宇1)郑朝阳2)苏艳1)†赵纪军1)

1)(大连理工大学,三束材料改性教育部重点实验室,大连 116024)2)(中国工程物理研究院流体物理研究所,冲击波与爆轰物理国家实验室,绵阳 621900)(2016年10月9日收到;2016年11月21日收到修改稿)

采用第一性原理密度泛函理论结合经典色散修正方法,对固态硝基苯在单轴压缩下的基本结构关系进行了计算.静水压缩和单轴压缩都压缩到初始平衡体积的70%.将静水压下优化后的晶胞体积、晶格参数以及平衡条件下的晶格能与实验值进行了比较,均符合较好.同时,为了充分地表征固态硝基苯的各向异性,将硝基苯沿着三个晶格矢量的方向进行单轴压缩,把每个方向的应力张量、能带带隙、每个原子能量的改变分别作为体积压缩比的函数进行了比较和分析.其中,最显著的各向异性效应是在体积压缩比为0.76时,沿X轴压缩导致硝基苯能带带隙闭合,体系呈金属化;而静水压缩或沿Y轴和Z轴压缩时体系始终呈半导体状态,带隙均大于1.59 eV.为了充分理解这一各向异性特性,我们计算了硝基苯晶体的局域态密度和电荷密度分布,并对金属化现象做出了合理的分析和解释.在不同的压力加载条件下,通过对不同物理量的计算,发现X轴方向是硝基苯晶体内部最敏感的方向.这些各向异性效应的研究将有助于人们在原子尺度上深入理解固态硝基苯的物理化学性质.

硝基苯,单轴压缩,静水压,含能材料

1 引 言

含能材料是一种运用于国防工业领域的重要材料,其自身存储着较高的化学能量,受到外界扰动可以快速地释放热量或气态产物.一般来说,含能材料分为炸药、推进剂和烟火剂等.在过去的数十年里,许多研究团队对含能材料的研究做了非常多的努力和贡献[1−4].充分理解材料的宏观特性与微观结构变化之间的关系是含能材料的研究热点,尤其是爆轰过程以及爆轰的初始阶段对于含能材料的研究至关重要.明确材料的爆轰行为与分子结构的关系,可以使我们更加深入地了解含能材料的性能,从而有效地设计出新型高效的炸药[5].然而,由于含能爆炸物实验研究的危险性以及实验数据的缺乏,理论模拟变得尤为重要,并且可以在一定程度上指导和辅助实验的进行.典型的含能材料通常是有机分子晶体,例如硝基甲烷、黑索金、FOX-7等[6−9].人们运用密度泛函理论,在原子和分子尺度上研究含能有机分子晶体在高压环境下的物理和化学性质,这对理解其高压行为(包括静水压缩和单轴压缩)有很大的帮助.

固态硝基苯(其化学式为C6H5NO2)通常作为含能分子晶体的原型体系而受到关注和研究,并在实验和理论方面均取得了一定的进展[10−17].实验上,通过X-射线衍射[10,11]、微波[12]、电子衍射[13]等技术测定硝基苯的晶体结构,如Boese等[10]和Trotter[11]先后在不同的温度条件下测定了常压下硝基苯的晶体结构.如图1所示,硝基苯的晶体结构属于P 21/c空间群、单斜晶系,且每个晶胞内包含4个硝基苯分子.在103 K时,硝基苯的实验晶格参数是:a=3.8014Å,b=11.6153Å,c=12.9843Å,β=94.98◦.由于硝基苯分子间存在弱相互作用,邻近的氢原子和氧原子能够形成氢键,使得硝基苯晶体形成与三氨基三硝基苯(TATB)晶体类似的层状结构[10,18,19].高压下,Kozu等[16]通过爆炸平面波生成器和金刚石对顶砧装置测得硝基苯的雨贡纽曲线和静水压缩的PV关系.Kobayashi和Sekine[17]利用单脉冲激光拉曼系统测定了硝基苯晶体的实时拉曼光谱,认为分子间作用力使NO2伸缩振动在冲击压缩下有较小的蓝移.

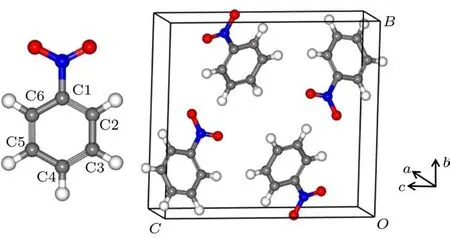
图1 硝基苯分子结构(左)和晶体结构(右)图Fig.1.The molecu lar structu re(left)and crystal structu re(right)of nitrobenzene.

在理论研究方面,Domenicano等[14]通过分子轨道方法研究了硝基苯分子的非平面构型.而Clarkson和Smith[15]采用B3 LYP/6-311+G**计算方案研究了硝基苯晶体的拉曼和红外振动光谱.Wang等[20]运用色散修正的密度泛函理论(DFT)计算了硝基苯在静水压0—10 GPa范围内分子结构的变化和拉曼振动模式.虽然有关硝基苯晶体的理论工作较少,但是为硝基苯的研究工作打下了基础.

固态硝基苯可以用作生产炸药的原料,而液态硝基苯往往是工业污水的成分之一,因此这两种状态的硝基苯的分解机理和过程被广泛关注[21−24].Pruitt和Goebbert[21]结合质谱分析方法和密度泛函理论计算,发现固态硝基苯等芳香族化合物π轨道上额外电子的作用,导致阴离子的C—N解离能比中性的C—N解离能要低.Dong和Sang[24]利用连续式全混流型反应系统观测到硝基苯在超临界水环境下能够首先分解为苯和硝酸盐,而硝基和超临界水的氧化作用使得反应进一步生成碳的一氧化物和二氧化物.

尽管这些理论和实验工作对硝基苯晶体的研究做了很大的努力,但在高压下固态硝基苯的结构转变以及应力分布等理论研究却很少.含能分子晶体单轴压缩[25−27]的研究可以得到晶体沿着不同方向的物理化学特性,所以对固态硝基苯晶体单轴压缩行为的研究是很有必要的.由于固态硝基苯可以看作是准正交的晶体结构,在本文中我们运用色散能量修正下的密度泛函理论[28,29]对单轴压缩下的硝基苯晶体进行了系统的计算研究.

2 计算方法

本文中的DFT计算[30]采用CASTEP(Cambridge Sequential Total Energy Package)程序[31]来完成. 离子和电子相互作用采用平面波基组下的模守恒赝势来近似描述,广义梯度近似下的Perdew-Burke-Ernzerhof(PBE)泛函[32]用于处理体系的交换关联势能.对于分子间的非共价弱相互作用的处理,采用Grimme[28]提出的经验的能量色散修正方案,即DFT-D2.运用Broyden-Fletcher-Gold farb-Shanno算法对晶体结构充分弛豫,其中设定每个原子的能量收敛标准是5.0×10−6eV,最大的力收敛标准是0.01 eV/Å,最大的晶胞应力收敛标准是0.02 GPa.体系能量截断能和布里渊区k点取样是决定控制DFT计算的关键参数[33],所以我们进行了一系列的收敛性测试来保证计算的数值精度,发现截断能取700 eV和k点平均间隔取0.05Å−1时,体系总能保持稳定,其收敛精度为1.6meV/atom.

初始的晶胞结构根据Boese等[10]的实验数据搭建,在对晶胞形状、晶格参数和原子坐标没有约束的条件下,对晶体结构进行了充分地弛豫,从而计算出0 K时平衡的晶体结构.其中,静水压缩时,外界对晶体结构从0 GPa开始持续加压直到20 GPa,且在压缩过程中,晶胞的体积、形状、晶胞中原子的坐标可以充分地弛豫.对于单轴压缩,我们保持单斜晶系和β角不变,分别只沿着三个坐标轴的方向之一进行单轴压缩(X轴对应晶格矢量a,Y轴对应晶格矢量b,Z轴对应晶格矢量c),在整个压缩过程中,每一步的压缩都保持2%的比例,直至达到其平衡体积的70%.单轴压缩时,固定晶胞形状,仅弛豫原子的坐标.

3 结果与讨论

3.1 静水压缩下硝基苯的结构变化

表1对计算得到的固态硝基苯的晶格参数和晶格能与实验数据做了比较.通过晶格参数的测定,不仅可以了解分子晶体的几何结构,也可以由此来判定所采用的理论方法对分子间相互作用描述的可靠程度.初始的硝基苯晶胞运用PBE泛函加色散修正方法得到充分的优化,与实验数据[10]进行比较,其中晶格参数a,b,c的误差分别是−2.98%,0.01%,−1.67%,而晶胞体积的误差是−4.35%.注意到实验是在103 K温度下,而我们的计算温度是0 K,因此推测温度效应是导致常压下晶格参数低估的原因之一.从计算结果来看,DFT-D方案低估了常压下的晶格参数.

体系的晶格能可以用来表征分子晶体中分子间相互作用的强度,其定义为气态分子与固态晶体之间的能量差.在本文中,将一个孤立的硝基苯分子放置在15Å×15Å×15Å的立方超元胞内模拟气态分子,计算得到的硝基苯晶格能是0.7243 eV,这与Caillet和Claverie[34]实验测得的硝基苯晶体晶格能在0.6635—0.6852 eV之间相比,高估了5.71%.结合对晶格参数的描述,我们认为DFT-D在常压下对分子间相互作用的描述并不充分,导致计算的晶格参数和晶格能与实验值比较有不同程度的误差.

为了考察硝基苯晶体在高压下结构的变化并检验色散修正方案在高压下描述晶体结构的可靠性,图2给出了理论计算和实验[16]的晶胞体积随压力的变化.从图2可以看出,随着压力的增大,晶胞体积单调递减.整体上,本文的计算很好地再现了体积随压力变化的趋势.然而,在给定的压力下,计算的晶胞体积比实验数据略小,推测这是由于DFT-D框架下对分子间作用力的描述不充分和上面提到的温度效应所导致的.但是,我们注意到随着压力的增大,相同压力下理论值与实验值更加接近.例如在0 GPa时,体积的偏差是−4.35%,而在接近4 GPa时,偏差约为−1.93%,这也意味着高压下DFT-D对分子间相互作用力的描述比较可靠.

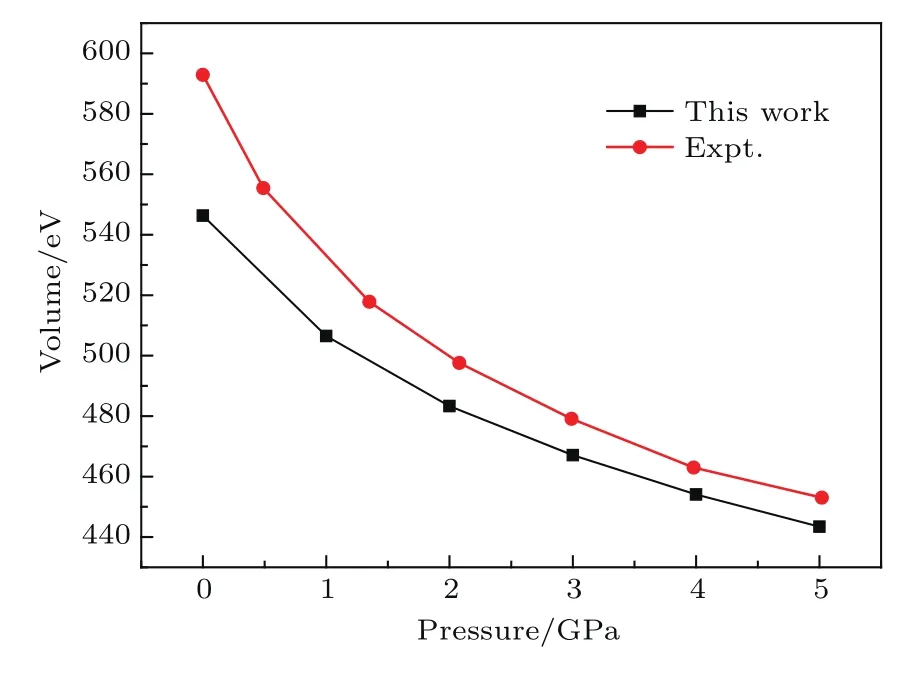
图2 晶胞体积随压力的变化Fig.2.The relationshipbetween the systempressure and unit cell volume.

为了检验高压下晶格参数的变化是否具有可靠性,图3给出了理论和实验的晶格参数随压力的变化,发现晶格参数a,b,c随压力的变化趋势与实验[16]保持了较好的一致.同时,本文的结果也同Wang等[20]在DFT-D框架下对硝基苯晶体在静水压缩下的计算结果基本一致.在5 GPa压力下,晶格参数a,b,c的体积压缩比分别为10.01%,3.30%,6.74%,可见a方向的体积压缩比明显大于b和c方向的体积压缩比.这主要源于硝基苯晶体中分子间氢键网络主要沿着晶格参数b和c所在平面内,导致氢键网络的层内b,c方向不易压缩,而层间方向a易压缩.

有机分子晶体往往存在分子间的氢键相互作用,虽然这种相互作用的强度比离子键、共价键要低,但却在凝聚态物质如层状固体、分子晶体中起到主导作用.图1是硝基苯分子的结构图,根据第一性原理计算,硝基苯晶体中C—H...O氢键的存在会对晶体的分子构型产生一定的影响.我们注意到以下三点:

表1 零压下晶格参数和晶格能与实验数据的比较Tab le 1.Comparison of experimental data with lattice parameter and lattice energy under the cond ition of zeropressure.

图3 压力依赖下的晶格参数的变化关系以及实验数据与理论值的比较Fig.3.Pressure dependence of lattice constants for Nitrobenzene.Experimental resu lts compared with present theoretical resu lts.

1)在气态硝基苯分子中,C—C键的长度关于C—N键对称分布,C1—C2,C2—C3,C5—C6和C6—C1键长均为1.396 Å,C3—C4和C4—C5键长均为1.400Å;当孤立的硝基苯分子形成晶体时,6个C—C键的键长发生了对称性的伸缩,C1—C2,C2—C3,C5—C6键长均为1.399Å,C6—C1键长为1.398Å,C3—C4和C4—C5键长均为1.393Å;

2)孤立硝基苯分子结合成晶体时,5个C—H键都一致地缩短了0.001—0.002Å,而C—N键的缩短最为明显,达到0.018Å;与此相反,两个N—O键却均伸长了0.006Å;

3)O=N键和O—N键向内收缩使得O=N—O角由124.85◦减小至123.35◦.

因此,从硝基苯形成晶体的分子几何构型变化可以看出,分子间相互作用起到了关键作用,不能忽视.

3.2 单轴压缩下硝基苯的结构性质

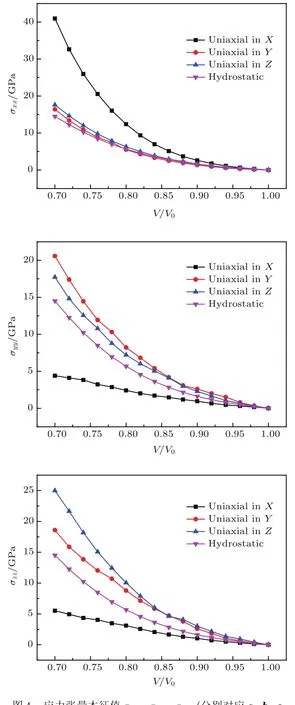
图4 应力张量本征值σxx,σyy,σzz(分别对应a,b,c晶格矢量)随体积压缩比的变化Fig.4.Relationshipbetween stress tensor eigenvalues σxx,σyy,σzz(corresponding tolattice vectors of a,b,c,respectively)and compression ratioV/V0.

为了模拟单轴压缩对硝基苯结构的影响,初始的晶格参数按照固定的比例进行了压缩.根据文献中研究单斜晶系应力张量的方案[25−27],我们对每个方向和每一步的单轴压缩时的主应力,即应力张量的本征值进行了测定.将应力张量的三个本征值σxx,σyy,σzz依次排序,并且标记为σ1,σ2,σ3.图4给出了每个单轴压缩方向上应力张量的三个主应力σ1,σ2,σ3随体积压缩比V/V0(取值范围在1—0.7)的变化.同时,静水压缩下的压力与体积压缩比的关系作为对比也呈现在图4中.对于不同的压缩方向,应力张量的三个本征值随体积压缩比表现出不同的变化趋势.三个主应力都随着体积压缩比的减小而增大,但是不同的变化幅度和趋势表现出硝基苯晶体各向异性的特征.其中,沿着Y轴和Z轴方向,主应力值σ1,σ2,σ3在不同方向之间的差值保持在1.2—6.4 GPa区间内.沿X轴方向的变化呈现出更加明显的可压缩性,在体积压缩比V/V0大于0.94时,主应力σ1沿X轴方向的增长率明显高于沿Y轴和Z轴方向的增长率,并且在体积压缩比V/V0等于0.7时,沿X轴方向压缩得到的主应力值σ1高达40.95 GPa,相当于沿Y轴(16.42 GPa)和Z轴(17.62 GPa)所得的主应力值的两倍之多.而对于主应力值σ2和σ3,沿X 轴压缩所引发的应力变化趋势却大相径庭,在体积压缩比V/V0等于0.7时,主应力值σ2沿X轴压缩的值是4.40 GPa,远远低于沿Y轴和Z轴对应的应力值.与σ2类似,主应力值σ3在体积压缩比V/V0达到0.7时仅为5.52 GPa,对于不同的压缩强度,σ3值的变化并不明显.综上所述,我们认为硝基苯晶体中,沿氢键网络的层间方向,即X轴方向,相对于Y轴和Z轴方向对于应力的变化更加敏感;且静水压缩作为单轴压缩的对比,静水压力都略低于沿Y轴和Z轴压缩的压力本征值.

在不同的压力加载条件下,对每个原子的能量变化也进行了计算.图5给出了沿着不同方向单轴压缩以及静水压缩时,平均每个原子能量随体积压缩比的变化.在图5中,同样可以观察到能量变化在三个方向上的各向异性行为.随着体积压缩比V/V0的增大,每个方向上原子的能量变化幅度也同时增大,并且由于单轴压缩方向晶格的束缚,单轴压缩时原子能量的变化总是大于静水压缩时能量的变化幅度.在体积压缩比V/V0等于0.86时,沿X轴方向原子的能量变化开始明显高于沿Y轴和Z轴方向,在V/V0为0.7时,能量变化率达到0.24 eV/atom.沿Y轴方向的能量变化曲线上,体积压缩比在0.8—0.78之间,能量出现微小的波动,即在体积压缩比0.8—0.78之间,每个原子的能量变化率增大.我们注意到,在应力随体积压缩比的变化中同样可以观测到类似的变化.

与此同时,我们还考察了硝基苯分子结构的变化,如图6所示.可以发现在体积压缩比V/V0为0.78—0.8时,硝基苯分子C—N键键长的变化幅度明显大于其他压缩区间,我们认为硝基苯分子C—N键键长的变化与每个原子能量的变化以及应力的变化有密切的关系,C—N键的键长幅度变化增大导致每个原子能量和应力及其变化率增大.在过去对含能分子晶体的理论研究中,比如TATB[18]和硝基甲烷[35],C—N键对压力的变化也比较敏感.因此我们推测在外界加载条件下,C—N键是影响硝基苯晶体物理化学性质变化的关键因素.

图5 单轴压缩与静水压缩下,每个原子的能量变化Fig.5.Change in energy per atomupon uniaxial and hyd rostatic compressions.

图6 C—N键长随体积压缩比的变化Fig.6.Change of C—N bond length under d iff erent kinds of compression.

能带带隙是描述晶体电子结构的重要物理量之一.图7给出了不同方向的单轴压缩与静水压缩下,硝基苯的能带带隙随体积压缩比的变化.相比于静水压缩和沿X轴方向压缩,沿着Y轴和Z轴压缩时体系的能带带隙缓慢地减小,而在体积压缩比V/V0大于0.8时,带隙的减小速率明显加快,并且在体积压缩比V/V0达到0.7时,带隙宽度趋于一致.对于沿X轴方向压缩,带隙的变化趋势表现出特有的规律,体积压缩比V/V0在1—0.76区间时,带隙宽度单调递减,减小率远远大于沿Y轴、Z轴压缩和静水压缩.在整个压缩区间内,沿X轴带隙宽度变化了2.25 eV,而沿Y轴、Z轴和静水压缩仅仅变化了0.77,0.54和0.86 eV.值得注意的是,沿X轴压缩并且体积压缩比V/V0达到0.76,对应的体系平均压力为9.27 GPa时,体系的能带带隙闭合,硝基苯晶体由半导体转变为金属.这是由于硝基苯晶体中X轴方向是氢键网络的层间方向,因此在X轴方向容易压缩使体系金属化.

为了进一步讨论金属化的晶体结构,图8给出了发生金属化转变时硝基苯晶体的总态密度和分态密度.从总态密度图可以看到:在费米能级附近,价带顶的峰来源于p态电子的贡献,而价带顶其他的峰值来源于s态和p态电子的贡献,同时导带底的峰值也主要来自p态电子的贡献.Cui等[36]在β-HMX(奥克托今)晶体电子结构的研究中也得到了类似的结论.在分态密度图中,我们可以看出在价带顶和导带底的峰值主要来自C,O,N原子p态电子的作用.值得注意的是,C原子s态和p态电子对所有峰值的贡献都大于其他原子,特别是费米能级上的电子态主要来自于C原子的p态.我们注意到,在零压平衡条件(即V/V0=1)下,硝基苯层间距离(即沿着a方向的近邻苯环之间的距离)为3.326Å,当V/V0等于0.76,即体系金属化时,苯环间的距离缩短为2.680Å.所以,我们构造了包含层状结构的超胞来计算V/V0=1和0.76时体系的电荷密度图,图9(a)和图9(b)分别表示硝基苯在常压下和金属化时的电荷密度.从图9可以看出,在结构金属化时,苯环上的部分电荷发生重叠,而硝基上的电荷没有发生重叠,也就是说近邻苯环上的π电子发生了一定的交叠.因此我们推断体系金属化是由于C原子上离域π电子导致的.

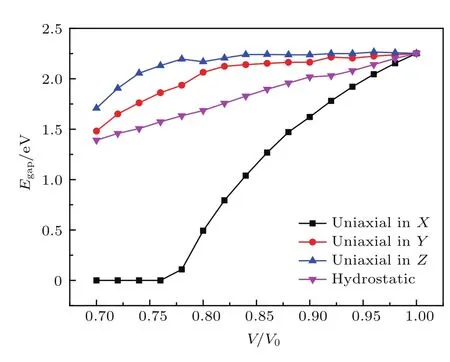
图7 单轴压缩与静水压缩下能带带隙随体积压缩比V/V0的变化Fig.7.Changes in band gapupon uniaxial and hyd rostatic compressions as a function of V/V0.

图8 硝基苯晶体金属化时的分态密度图,虚线表示费米能级Fig.8.Partial density of states(PDOS)of nitrobenzene at metallization cond ition.The Fermi energy is shown as a dashed vertical line.

图9 (a)常压下体系电荷密度图;(b)金属化时体系电荷密度图Fig.9.(a)Charge density of systemunder ambient cond ition;(b)charge density of systemat metallization.

3.3 硝基苯晶体单轴压缩下的剪切应力

剪切应力是引起材料塑性形变的重要驱动力,也是表征材料或者晶体各向异性的主要物理量之一.对剪切应力的计算有利于我们进一步地理解含能分子晶体中由冲击波引起的各向异性特征,可以通过对晶体特定的晶向实施单轴压缩实现冲击波加载.因此,我们根据应力张量的三个本征值,通过方程τ=(σi−σj)/2来计算体系内部不同的剪切应力值,其中,τ表示剪切应力;i/j,两者取值范围都是1,2,3.剪切应力τxy可通过i=1和j=2计算得到,同理在i=1,j=3和i=2,j=3时可计算得到τxz和τyz.根据计算结果,我们发现剪切应力τxy和τxz在不同的压缩方向上远远大于剪切应力τyz,使得硝基苯晶体的各向异性特征更加明显,因此这里我们重点讨论τxy和τxz在不同压缩方向的行为.图10(a)和图10(b)中给出了τxy和τxz在不同压缩方向上随体积压缩比V/V0的变化.体积压缩比在1—0.92范围内,剪切力τxy沿X,Y,Z轴三个单轴压缩方向基本没有差异并且保持着较低的压力值,但体积压缩比V/V0=0.92后,沿X轴方向的剪切力呈指数型增大,在体积压缩比V/V0=0.7时,该方向的剪应力值高达18.28 GPa,而沿着Y轴和Z轴压缩的剪应力只有2.08 GPa和0.05 GPa.而对于剪应力τxz,其变化趋势与τxy非常相似,在体积压缩比V/V0等于0.9以后,沿三个方向压缩产生的剪应力表现出明显不同的变化趋势,沿Y轴和Z轴增长幅度依然保持在0—4 GPa内,体积压缩比V/V0=0.7时,剪应力τxz沿X轴方向压缩也达到了17.72 GPa.因此,通过对剪切应力的分析,我们进一步理解了硝基苯晶体的各向异性,同时可以再次预言X轴方向是硝基苯晶体中最敏感的方向.

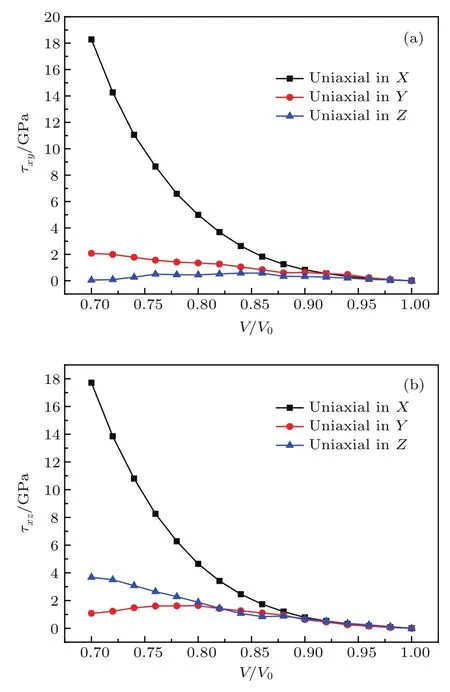
图10 单轴压缩下切应力随体积压缩比的变化 (a)τxy;(b)τxzFig.10.Change of shear stresswith compression ratioupon uniaxial compression:(a) τxy;(b) τxz.

4 结 论

本文通过密度泛函理论结合能量修正方案DFT-D2,对硝基苯晶体在静水压缩和单轴压缩下的结构和各向异性特征进行了系统的计算研究.在静水压缩下,DFT-D方案低估了常压下的晶胞体积和晶格参数a,b,c.而在高压下,计算的晶胞体积与实验值很接近,比如在4 GPa时误差在1%以内,计算结果比较可靠.同时计算得到的硝基苯晶体的晶格能与实验得出的晶格能相比,能量范围略有高估,误差为5.7%.综合考虑这些计算得到的物理量及其与实验的误差,我们可以认定PBE泛函结合能量修正(DFT-D2)的方法对于描述硝基苯晶体的结构以及随后的单轴压缩计算是可靠的.

我们对硝基苯晶体在X,Y,Z晶轴方向进行了单轴压缩研究,在每一个压缩方向上,计算了相应的应力张量、剪切应力、带隙宽度、每个原子的能量.计算结果显示了硝基苯晶体在单轴压缩下的各向异性特征.首先,对于应力张量的三个本征值σ1,σ2,σ3,沿X轴方向压缩的σ1值远高于沿Y轴和Z轴的应力值,而沿X轴方向压缩得到的σ2和σ3值又远小于其他两个方向.其次,对于体系的带隙宽度,沿X轴方向压缩时,在体积压缩比V/V0达到0.76时,带隙闭合,体系呈金属化,源于近邻分子中苯环之间离域π电子轨道的重叠.而对于每个原子的能量变化,同样也是沿着X轴压缩能量变化最大.最后,我们对体系中最大的两个剪切应力τxy和τxz进行了分析,发现沿X轴压缩得到的剪切应力值都远远大于沿Y,Z轴方向.因此,我们推测硝基苯晶体内部X轴方向比Y和Z轴方向更加敏感.在实验上,沿着这三个晶轴方向进行冲击压缩,将呈现出不同的宏观物性变化规律.

[1]Zheng Z Y,ZhaoJ J 2016Chin.Phys.B25 076202

[2]Sikder A,Sikder N 2004J.Hazard.Mater.112 1

[3]Politzer P,Mu rray J S,SeminarioJ M,Lane P,G rice ME,Concha MC 2001J.Mol.Struc.:Theochem573 1

[4]Zheng Z Y,ZhaoJ J 2015Chin.J.High Pressure Phys.29 81(in Chinese)[郑朝阳,赵纪军 2015高压物理学报29 81]

[5]Fried L E,Manaa MR,Pagoria P F,Simpson R L 2001Annu.Rev.Mater.Res.31 291

[6]Zhang L,Chen L 2013Acta Phys.Sin.62 138201(in Chinese)[张力,陈朗2013物理学报 62 138201]

[7]Cheng HP,Dan J K,Huang Z M,Peng H,Chen G H2013Acta Phys.Sin.62 163102(in Chinese)[程和平,但加坤,黄智蒙,彭辉,陈光华2013物理学报62 163102]

[8]Meng Z R,Zhang W B,Du Y,Shang L P,Deng H2015Acta Phys.Sin.64 073302(in Chinese)[孟增睿,张伟斌,杜宇,尚丽平,邓琥2015物理学报64 073302]

[9]Zhang L,Chen L 2014Acta Phys.Sin.63 098105(in Chinese)[张力,陈朗2014物理学报 63 098105]

[10]Boese R,Bläser D,Nussbaumer M,Krygowski TM1992Struct.Chem.3 363

[11]Trotter J 1959Acta Crystallogr.12 884

[12]Larsen N W 2010J.Mol.Struct.963 100

[13]BorisenkoKB,Hargittai I1996J.Mol.Struct.382 171

[14]DomenicanoA,Schu ltz G,Hargittai I,ColapietroM,Portalone G,George P,Bock C W 1989Struct.Chem.1 107

[15]C larkson J,Smith W E 2003J.Mol.Struct.655 413

[16]Kozu N,AraiM,Tamu ra M,Fu jihisa H,AokiK,Yoshida M2000Jpn.J.Appl.Phys.39 4875

[17]Kobayashi T,Sekine T2000Phys.Rev.B62 5281

[18]Liu H,ZhaoJ,Du J,Gong Z,Ji G,W ei D 2007Phys.Lett.A367 383

[19]Chen F,Zhang H,ZhaoF,Li Q l,Qu J Y 2008J.Mol.Struc.:Theochem.864 89

[20]W ang W P,Liu F S,Liu Q J,Liu Z T2016Comput.Theor.Chem.1075 98

[21]Pruitt C J M,Goebbert D J 2013Chem.Phys.Lett.580 21

[22]Fayet G,Joubert L,Rotureau P,AdamoC 2008J.Phys.Chem.A112 4054

[23]Pein BC,Sun Y,D lott D D 2013J.Phys.Chem.A117 6066

[24]Dong S L,Sang D P 1996J.Hazard.Mater.51 67

[25]Con roy M,Oleynik I,Zybin S,W hite C 2008Phys.Rev.B77 094107

[26]Conroy M,Oleynik I,Zybin S,W hite C 2009J.Phys.Chem.A113 3610

[27]Margetis D,Kaxiras E,E lstner M,FrauenheimT,Manaa MR 2002J.Chem.Phys.117 788

[28]G rimme S 2011W ires.Comput.Mol.Sci.1 211

[29]G rimme S,Antony J,Ehrlich S,Krieg H2010J.Chem.Phys.132 154104

[30]Parr R G,Yang W 1995Annu.Rev.Phys.Chem.46 701

[31]Segall M,Lindan P J,Probert MA,Pickard C,HasnipP,Clark S,Payne M2002J.Phys.:Condens.Mat.14 2717

[32]PerdewJP,Burke K,ErnzerhofM1996Phys.Rev.Lett.77 3865

[33]Monkhorst HJ,Pack J D 1976Phys.Rev.B13 5188

[34]Caillet J T,C laverie P 1975Acta Crystallogr.Sec.A31 448

[35]Liu H,ZhaoJ J,W ei D Q,Gong Z Z 2006J.Chem.Phys.124 124501

[36]Cui HL,Ji G F,ZhaoJ J,ZhaoF,Chen X R,Zhang Q M,W ei D Q 2010Mol.Simulat.36 670

PACS:61.50.Ks,61.50.Lt,71.20.–bDOI:10.7498/aps.66.036101

First-principle simu lation of solid n itrobenzene under un iaxial compression∗

Fan Jun-Yu1)Zheng Zhao-Yang2)Su Yan1)†ZhaoJi-Jun1)

1)(Key Laboratory ofMaterials Mod ifi cation by Laser,Ion and E lectron Beams,Dalian University of Technology,Ministry of Education,Dalian 116024,China)2)(National Key Laboratory of Shock Wave and Detonation Physics,Institute of Fluid Physics,China Academy of Engineering Physics,Mianyang 621900,China)(Received 9 October 2016;revised manuscript received 21 November 2016)

Energeticmaterials(EMs)including explosives,propellants and pyrotechnics have been widely used for themilitary and many other purposes.Solid nitrobenzene(an organic molecular crystal)cou ld be considered as a prototype of energetic material.Uptonow,numerous studies have been devoted tocrystal structures,spectrumproperties and decomposition mechanisms for solid nitrobenzene experimentally and theoretically.However there has been a lack of the comprehensive understanding of the anisotropic characteristics under diff erent loading conditions.Thus we investigate the hydrostatic and uniaxial compressions along three diff erent lattice directions todetermine this anisotropic eff ect.In this work,the density functional theory calculations are performed based on Cambridge Sequential Total Energy Package(CASTEP)code using normconserving pseudopotentials and a kinetic energy cutoff of 700 eV.The generalized gradient approximation with the Perdew-Burke-Ernzerhof parameterization is used.Monkhorst-Pack k-point meshes with a density of 0.05 Å−1are used for Brillouin-zone integration.The empirical dispersion correction by G rimme is taken toaccount for week intermolecular interactions.The hyd rostatic compressions are applied from0 GPa to20 GPa.Cell volume,lattice shape and coordinates of the atoms cou ld be fully relaxed.while uniaxial compression is applied upto70%of the equilibriumcell volume in steps of 2%along their lattice directions respectively.At each compression step,on ly atomic coordinates are allowed torelax,with the lattice fixed.The equilibriumlattice structures under hydrostatic compressions are obtained by full relaxation at 0 Ktemperature.In ambient condition,the calcu lated volume and parameter of the unit cellare underestimated compared with the experimentaldata,and corresponding errors are−2.98%,0.01%,−4.39%,5.71%respectively.In contrast,the calculated lattice energy is overestimated compared with the range of experimental resultswith 5.71%of the error.In high pressure condition,the volume and cell parameter of the unit cell as a function of compression ratioare plotted and compared with the experimental data.The theoretical and experimental values are close with the increase of the pressure,for instant,the error decreases from−4.39%at 0 GPa to−1.93%at 4 GPa.On the other hand,the uniaxial compression is applied along the directions of three lattice vectors.The changes of stress tensor,band gap,energy per atomas a function of compression ratioare alsoplotted and discussed,which can characterize the anisotropic eff ect of solid nitrobenzene.Themost noticeable eff ect of anisotropy in solid nitrobenzene is themetallization at V/V0=0.76 compressed along the X axis,while the solid nitrobenzene under hyd rostatic pressure or other uniaxial compressions uptoV/V0=0.76 remains semiconductor with band gaplarger than 1.591 eV.By analyzing the local density of states and charge density distribution of nitrobenzene crystal,we con fi rmthat the metallization is caused by the overlapof theπelectron frombenzene ring.Through calculating diff erent physical parameters,we find that X axis is themost sensitive direction of nitrobenzene crystal.The studies of anisotropic eff ects are expected toshed light on the physicaland chemical propertiesof solid nitrobenzene on an atomistic scale and provide several insights for experiments.

nitrobenzene,uniaxial compression,hydrostatic pressure,energeticmaterials

10.7498/aps.66.036101

∗国防基础科研核基础科学挑战计划(批准号:JCKY 2016212A501)、国家自然科学基金(批准号:11674046)、中国博士后科学基金(批准号:2016M592704)和大连理工大学超算中心资助的课题.

†通信作者.E-mail:su.yan@d lu t.edu.cn

*Project supported by the Science Challenging Programof the National Defense Basic Scientifi c Research of China(G rant No.JCKY 2016212A501),the National Natural Science Foundation of China(G rant No.11674046),the China Postdoctoral Science Foundation(G rant No.2016M592704),and the Supercompu ting Center of Dalian University of Technology,China.

†Corresponding au thor.E-mail:su.yan@d lut.edu.cn