土钉墙潜在破裂面确定方法
2017-07-31李建军冯振桥郭玉涛李相斌
李建军, 冯振桥, 董 洁, 郭玉涛, 李相斌
(中北大学 理学院, 山西 太原 030051)
土钉墙潜在破裂面确定方法
李建军, 冯振桥, 董 洁, 郭玉涛, 李相斌
(中北大学 理学院, 山西 太原 030051)
土钉墙潜在破裂面的位置和形态对土钉的抗拔承载力计算具有重要作用. 基于潜在破裂面土体剩余下滑力和滑移区钉土作用力之间的相互关系, 提出了一种确定土钉墙潜在破裂面的新方法. 该方法认为滑移区土钉最大轴力位置与土钉墙潜在破裂面应相互重合, 通过计算滑移区分层土钉最大轴力, 可以确定土钉墙潜在破裂面. 并指出不同土压力的分布形式对土钉最大轴力和潜在破裂面的分布形式具有较大影响. 最后结合法国CEBTP大型试验1号墙实测数据, 分析了五边形土压力、 Peck土压力、 铁路规范土压力和基坑规范土压力4种土压力分布模式对土钉墙潜在破裂面确定的影响大小. 理论分析表明, 利用五边形土压力分布模式, 采用上述方法确定的土钉墙潜在破裂面与实测破裂面形态较为一致, 计算滑移区面积与实测滑移区面积比为0.94, 计算潜在破裂面与实测破裂面之间的水平距离平方和为0.917.
土钉墙; 潜在破裂面; 土压力分布模式; 钉土作用
0 引 言
土钉墙是目前普遍应用的一种边坡支护形式, 其侧向土压力的分布形式和破裂面形态对土钉受力计算和变形分析起着重要的作用. 工程设计中, 土钉墙潜在破裂面主要是根据技术规范推荐的方法确定, 如直线破裂面[1]和双折线破裂面[2]. 朱彦鹏等[3-4]认为土钉在边坡稳定区长度和直径的改变将会引起最危险滑移面位置的改变, 由此通过编写计算机软件, 自动搜索每级开挖过程中这种动态变化的最危险滑移面位置, 从而设计土钉的长度和直径大小. 袁洪升[5]则指出土体中设置土钉后, 改变了土体的应力状态, 主应力方向发生偏转, 土体的滑裂面相应改变. 惠趁意等[6]假定滑动面为抛物线形, 利用几何关系和积分法建立了最危险滑移面搜索模型, 推导了稳定性系数的求解公式. 李忠等[7]将有限元计算与多种群遗传算法(MPGA)相结合, 建立了一种基于MPGA的复杂应力状态边坡稳定性分析通用模型, 通过数值应力场求解安全系数, 由此得到最危险破裂面. 陈肇元等[8]认为土钉墙作为一种被动支护形式, 处于极限平衡时, 破裂面两侧分为滑移区和稳定区, 土钉的最大轴力出现在潜在破裂面处. 周勇等[9]根据土钉墙滑动面的不同类型, 讨论和优化了建筑基坑支护技术规程中土钉墙整体稳定安全系数计算公式. 王辉等[10]通过二阶距法对土钉墙内外部的极限状态功能函数进行了可靠度分析. 吴九江等[11]基于详细的现场监测数据并辅以有限元数值计算, 分析了边坡开挖过程中土钉-预加固桩复合支护体系的受力和变形变化规律. 廖瑛等[12]从可靠度角度对土钉墙整体滑移和倾覆稳定性问题进行了分析. 尽管诸多学者从不同角度阐述了土钉墙的受力机理, 但很少有研究讨论土压力的分布模式对土钉墙潜在破裂面的影响. 被加固土体中设置土钉后, 钉土相互作用引起的土钉轴力和土压力分布模式对土钉墙潜在破裂面形态具有重要影响. 本文对潜在破裂面外侧的滑移区土体和土钉分别进行受力分析, 认为边坡进行土钉支护后, 滑移区土钉承受上覆土压力的轴向分力, 钉土相对滑动后, 又要承受钉土相互作用的摩擦力, 上覆土压力的轴向分力作用于土钉轴线且方向指向稳定区, 对边坡稳定有利, 因此, 建立了滑移区土钉受力与剩余下滑力之间的平衡方程, 进而确定了土钉墙潜在破裂面位置, 同时讨论了不同土压力分布形式对土钉墙潜在破裂面的影响.
1 土钉轴力机理分析
1.1 滑动体受力分析
对于一个坡面陡立的斜坡, 当处于极限平衡状态时, 坡体内形成一个潜在破裂面, 潜在破裂面两侧分别为滑移区和稳定区. 对滑移区土体进行受力分析可知, 沿破裂面存在下滑力F0和抗滑力F1, 如果F0=F1, 说明土体处以极限平衡状态; 如果F0
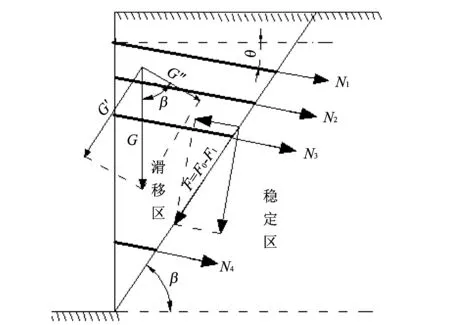
图 1 土钉墙边坡受力示意图Fig.1 Stress diagram of soil nailing wall slope
取单位宽度对土钉支护坡体进行受力分析, 可建立如下方程
下滑力
抗滑力
剩余下滑力
土钉最大轴力
式中:β为潜在破裂面与水平方向的夹角;θ为土钉与水平面的夹角;φ为土体内摩擦角;c为土体粘聚力;s为破裂面长度.
1.2 土钉微单元体受力分析
对滑移区土钉轴力进行分析, 基于以下几点假设建立对等关系式:
1) 每根土钉所穿越的土体土质均匀;
2) 土钉不会发生屈服破坏, 土钉墙的破坏主要为钉土界面之间的剪切破坏;
3) 忽略土钉与土钉之间的相互作用和土钉加筋作用而造成的土体内摩擦角的变化;
4) 忽略土钉钉头力的作用.
假设滑移土体处于极限平衡状态, 土钉与水平面的倾角为θ, 取土钉为研究对象, 选取土钉距钉头距离x的微段dx进行受力分析. 在微段dx上部作用单位土柱重力G(x), 下部土体对土钉的单位支撑力为Q(x), 重力G(x)可分解为垂直土钉轴线的分力G(x)cosθ和平行于土钉轴线的分力G(x)sinθ, 支撑力Q(x)与G(x)的垂直分力G(x)cosθ平衡, 平行于土钉轴线的分力G(x)sinθ使钉土之间存在相对滑动, 设钉土之间的单位摩擦力为f(x), 土钉微元体受力情况如图 2 所示.

图 2 滑动区土钉微元体受力图Fig.2 The force diagram of soil nailing infinitesimal body in sliding zone
沿土钉轴线方向建立平衡方程
N(x)+f(x)dx=
N(x)+dN(x)+G(x)sinxdx,
dN(x)=f(x)dx-G(x)sinxdx.
对上式积分, 并展开可得


式中:h为钉头到坡顶的距离;l0为单根土钉在滑移区的长度;D为土钉直径;γ为坡体岩土体重度;μ为钉土界面摩擦系数, 其数值可根据表 1 选取[8].

表 1 钉土摩擦系数
1.3 分步开挖的影响
假设每次开挖都开挖到对应土钉设计位置, 第一步开挖到第1排土钉位置, 打入土钉, 由于土体结构性使土体存在天然强度, 可以认为第一步开挖后土坡是稳定的. 然后进行第二步开挖至第2排土钉位置处, 施工第2排土钉, 此时对坡体产生作用的仅为第1排土钉. 假设土坡没有设置土钉前的潜在破裂面为库伦破裂面, 破裂面与水平面呈 45°+φ/2, 如图3(a)中实线所示. 设置土钉后, 坡体中应力重分布, 由前述可知, 潜在破裂面与土钉交汇处为土钉轴力最大处, 由此连接坡脚与第一根土钉轴力最大处, 形成第一个潜在破裂面的下段, 再由第一根土钉轴力最大处按 45°+φ/2 向坡顶延伸, 形成第一个潜在破裂面的上段, 如图3(b)中粗虚线所示. 由于土钉发挥作用, 土钉需要提供的力的大小为剩余下滑力F沿土钉轴向的分力, 由于假设破裂面与计算破裂面之间不重合, 沿土钉轴线方向, 假设破裂面与施加土钉后的计算破裂面之间存在轴力差Δ1,Δ1可按式(6)计算

开挖第三步时, 又会破坏坡体先前的平衡, 同时第2排土钉开始发挥作用, 坡体应力发生再分布后达到新的平衡. 如前所述可以分别计算第三步开挖后第1排和第2排土钉的轴力最大点, 依次连接坡脚和第1排和第2排土钉的轴力最大点, 再由第一根土钉轴力最大点按45°+φ/2向坡顶延伸, 形成第二个计算潜在破裂面, 如图3(c)中粗虚线所示. 如此依次循环, 直到计算到最后一步坡体开挖, 并连接坡脚与各排土钉的最大轴力计算点, 由第一根土钉最大轴力处按45°+φ/2向坡顶延伸, 就是所求计算潜在破裂面.
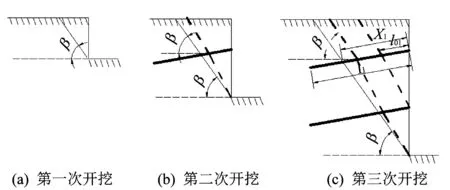
图 3 分步开挖示意图Fig.3 Step-by-step excavation schemes
1.4 破裂面的确定
假设距离坡顶距离为h的第i排土钉承担整个破裂面剩余下滑力的分担比为ni, 则联合式(5)和式(6)有
niFcos(β+θ)+Δi=

求解, 可得
式中, 计算系数A、B、C按下式确定

求出每排土钉在滑移区的长度l0后, 每排土钉l0的端点连线就是潜在破裂面的形状和位置.
式中第i排土钉的分担比ni与面层土压力的分布形式及土钉所处的位置有关, 本文采用土钉钉头位置所分担土压力与坡体侧向总土压力的比值确定ni,ni可由下式表示
式中:pi为侧向土压力.
土压力pi需根据坡体每步开挖后侧向土压力的形式确定, 目前, 对于土钉墙侧向土压力的分布形式还存在不同的认识, 下面对其作简要介绍, 并在后面算例中讨论不同土压力分布模式对潜在破裂面的影响.
1) 五边形法[13].
五边形土压力分布为中上部大、 两头小, 将土压力分布图简化成3部分, 如图 4 所示. 开挖面以下的影响深度约为开挖面深度的20%~60%, 设边坡开挖深度为H′, 边坡开挖影响深度H″=0.2H′~0.6H′, 土压力的分布确定如下
σ0=0.25K0γz.
当z≤0.25H′时,σz=K0γz;
当0.25H′≤z≤0.5H′时,σz=σ0;
当0.5H′≤z≤H′时,
σz=(H′+H″-z)/(0.5H′+H″)σ0.

图 4 五边形土压力分布图Fig.4 Soil pressure distribution of pentagon method
2)基坑土钉支护技术规程[14].
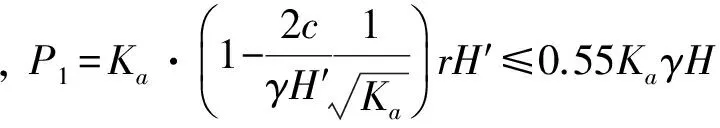
3) 铁路路基支挡结构设计规范[2].
铁路路基支挡结构设计规范土压力(以下简称铁路土压力)分布如图5(b)所示.


式中:λa为库仑主动土压力系数;α为墙背与竖直面间的夹角;δ为墙背摩擦角.
4) Peck土压力[15].
Peck土压力分布如图5(c)所示.
砂土:P1=0.65kaγH′.
软粘土:
(γH′/c>4)∶P1=
(1-4c/γH′)γH′>0.3γH′.
硬粘土:
(γH′/c<4)∶P1=0.2γH′~0.4γH′.

图 5 不同土压力分布模式图Fig.5 The distribution pattern of different soil pressure diagram
2 案例分析与讨论
为了进一步说明式(7)~(12)计算土钉潜在破裂面的合理性, 下面以法国CEPTP大型试验CLOUTERRE项目1号墙试验结果对其进行验证[16]. 该试验墙面垂直, 高7m, 宽7.5m, 土体采用中密砂, 土体重度γ=16.9 kN/m3, 内摩擦角φ=38°, 粘聚力c=3 kPa, 土钉水平间距1.15 m, 第一根土钉距坡顶0.5 m, 向下土钉竖向间距为1 m, 土钉孔径为63 mm, 土钉与水平面倾角为10°.
图 6 为采用式(7)~(12)按照不同土压力分布计算的潜在破裂面与实测破裂面对照图, 不同土压力分布模式对潜在破裂面的形态影响较大. 总体来看, 五边形土压力计算的潜在破裂面与实际破裂面最接近, Peck土压力计算的潜在破裂面与实测破裂面偏差最大. 基坑土压力和铁路土压力计算的潜在破裂面虽然顶部较接近实测破裂面, 但第3~5排土钉计算的潜在破裂面与实测破裂面偏差较大.


图 7 破裂面差方和计算示意图Fig.7 Calculating diagram of error sum of squares

表 2 潜在破裂面的面积比与差方和
由表 2 可以看出, 从差方和角度比较, Peck土压力最大, 为9.329; 铁路土压力和基坑土压力均超过1.0, 分别为1.384和1.491; 五边形土压力最小, 为0.917. 差方和越大, 则说明计算潜在破裂面与实测破裂面局部差别越大.
结合图6, 从面积比进行比较, Peck土压力计算潜在破裂面面积比为1.088, 但Peck土压力的差方和为9.329, 差别较大, Peck土压力计算潜在破裂面上部在实测破裂面右侧, 进入边坡稳定区, 造成设计土钉长度不必要的增加; 中下部计算破裂面严重偏离到实测破裂面左侧, 造成土钉设计长度不足, 可能引起边坡失效. 铁路土压力和基坑土压力计算潜在破裂面面积比分别为0.839 和0.848, 第1排和第2排土钉计算潜在破裂面与实测破裂面相差不大, 但中下部计算破裂面偏离到实测破裂面左侧, 由此造成差方和较大, 分别为1.384和1.491, 也可造成土钉设计长度不足, 可能引起边坡失效. 五边形土压力面积比为0.94, 接近1, 说明计算滑移区面积与实测滑移区面积相差不大, 差方和为0.917, 计算潜在破裂面与实测破裂面空间位置相差也不大, 由此可以看出五边形土压力计算土钉墙潜在破裂面更接近实测破裂面, 计算较为合理. 但五边形土压力计算的土钉墙靠近墙脚的几排土钉的安全系数也相对偏小, 所以在今后应用中应引起注意.
3 结 论
1) 在不考虑土钉加筋作用造成的土体内摩擦角变化的情况下, 对滑移区土钉的钉土相互作用进行了受力分析, 建立了土体剩余下滑力与滑移区土钉作用力之间的平衡方程, 提出了通过计算滑移区土钉轴力最大点确定土钉墙潜在破裂面的计算方法.
2) 根据法国CEPTP试验项目1号墙测试结果, 利用面积比和差方和, 定量讨论了五边形土压力、 Peck土压力、 铁路土压力和基坑土压力4种土压力分布模式对土钉墙计算潜在破裂面的影响, 分析认为五边形土压力应用于土钉墙潜在破裂面的确定较为合理.
[1]建筑基坑支护技术规程(JGJ120-2012)[S]. 北京: 中国建筑工业出版社, 2012.
[2]铁路路基支挡结构设计规范(TB10025-2006)[S]. 北京: 中国铁道出版社, 2006.
[3]朱彦鹏, 李忠. 深基坑土钉支护稳定性分析方法的改进及软件开挖[J]. 岩土工程学报, 2005, 27(8): 939-943. Zhu Yanpeng, Li Zhong. Improvement on stability analysis of soil nailing in foundation excavations and its software development[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(8): 939-943. (in Chinese)
[4]朱彦鹏, 王秀丽, 李忠, 等. 土钉墙的一种可靠性自动优化设计法[J]. 岩石力学与工程学报, 2006, 25(增1): 3123-3130. Zhu Yanpeng, Wang Xiuli, Li Zhong, et al. Optimal design method of reliability for soil nailed walls[J]. Chinese Journal of Rock Mechanics Engineering, 2006, 25(S1): 3123-3130.(in Chinese)
[5]袁洪升. 土钉墙支护结构破裂角的研究[J]. 施工技术, 2011, 40(7): 41-43. Yuan Hongsheng. Research on rupture angle of soil-nailing wall structure[J]. Constructious Technology, 2011, 40(7): 41-43. (in Chinese)
[6]惠趁意, 朱彦鹏, 叶帅华. 预应力锚杆复合土钉支护边坡稳定性分析[J]. 岩土工程学报, 2013, 35(增2): 325-329. Hui Chenyi, Zhu Yanpeng, Ye Shuaihua. Stability analysis of composite soil-nailing wall with prestressed anchors[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 325-329. (in Chinese)
[7]李忠, 杨俊. 基于MPGA的复杂应力状态边坡稳定性分析[J]. 岩土力学, 2015, 36(5): 1488-1495. Li Zhong, Yang Jun. Stability analysis of slope under complex stress conditions based on multi-population genetic algorithm[J]. Rock and Soil Mechanics, 2015, 36(5): 1488-1495. (in Chinese)
[8]陈肇元, 崔京浩. 土钉支护在基坑中的应用[M]. 北京: 建筑工业出版社, 2000.
[9]周勇, 王正振. 土钉墙内部稳定性分析方法改进[J]. 岩土力学, 2016, 37(增2): 356-362. Zhou Yong, Wang Zhengzhen. Improvement of internal stability analysis method of soil nailing wall[J]. Rock and Soil Mechanics, 2016, 37(S2): 356-362. (in Chinese)
[10]王辉, 杨向前, 郜新军. 加锚复合土钉支护体系可靠度分析与实证[J]. 广西大学学报(自然科学版), 2016, 41(1): 212-218. Wang Hui, Yang Xiangqian, Gao Xinjun. Reliability analysis and demonstration of composite soil nailing retaining system enhanced with prestressed anchor[J]. Journal of Guangxi University (Natural Science Edition), 2016, 41(1): 212-218. (in Chinese)
[11]吴九江, 程谦恭, 孟祥龙. 黄土高边坡土钉-预加固桩复合支护体系性状分析[J]. 岩土力学, 2014, 35(7): 2029-2040. Wu Jiujiang, Cheng Qiangong, Meng Xianglong. Behavior of a high steep loess slope strengthened by combination system of soil nails and stabilization piles[J]. Rock and Soil Mechanics, 2014, 35(7): 2029-2040. (in Chinese)
[12]廖瑛, 孙雷江, 刘旭. 随机变量对土钉墙抗外部稳定可靠性的影响分析[J]. 科学技术与工程, 2013, 13(23): 6934-6938. Liao Ying, Sun Leijiang, Liu Xu. Analysis on the random variables’influence on outside stability of soil nailed wall[J]. Science Technology and Engineering, 2013, 13(23): 6934-6938. (in Chinese)
[13]刘晓红, 饶秋华. 土钉支护侧土压力合理分布模式探讨[J]. 中南公路工程, 2006, 31(2): 29-32. Liu Xiaohong, Rao Qiuhua. More reasonable model for the lateral soil pressure distribution of soil nail bracing[J]. Journal of Central South Highway Engineering, 2006, 31(2): 29-32.(in Chinese)
[14]基坑土钉支护技术规程(CSCS 96: 97)[S]. 北京: 中国工程建设标准化协会, 1997.
[15]魏焕卫, 杨敏, 孙剑平, 等. 土钉墙变形的实用计算方法[J]. 土木工程学报, 2009, 42(1): 81-90. Wei huanwei, Yang Min, Sun Jianping, et al. Calculation method for soil nailing displacement[J]. China Civil Engineering Journal, 2009, 42(1): 81-90.(in Chinese)
[16]Plumelle C, Scholsser F, Delage P, et al. French national research project on soil nailing: CLOUTERRE[C]. Design and Performance of Earth Retaining Structures, ASCE, 1991: 660-675.
Determination Method of Soil Nailing Wall’s Potential Slipping Surface
LI Jian-jun, FENG Zhen-qiao, DONG Jie, GUO Yu-tao, LI Xiang-bin
(School of Science, North University of China, Taiyuan 030051, China)
The position and shape of soil nailing wall’s potential failure surface plays an important role in calculation of uplift bearing capacity of the soil nailing. Based on the interrelation between potential fracture surface’s soil residual sliding force and soil nailing force in slip zone, a new method was proposed to determine the potential failure surface of soil nailing wall. It is believed that soil nailing position of maximum axial force in slip zone and soil nailing wall potential failure surface should overlap each other, and the location of the potential failure surface of soil nail wall can be determined by calculating maximum axial force of layered soil nail in slip zone. Different distribution patterns of soil pressure have a large impact to on the maximum soil nail axial force and the position of potential failure surface. Finally according to the measured data of wall of CEBTP large scale experiment in France, the distribution patterns of soil pressure’s effect to the determination of soil nail wall potential fracture surface could be analyzed, such as Pentagon soil pressure, Peck soil pressure, railway soil pressure and the foundation pit soil pressure distribution patterns. Potential failure surface of soil nailing wall based on Pentagon soil pressure distribution pattern is comparative in accordance with the measured fracture surface. The area ratio of calculated slip zone and measured slip zone is 0.94, and the sum of squares of horizontal distance between calculated potential failure surface and measured fracture surface is 0.917.
soil nailing wall; potential slipping surface; soil pressure distribution model; soil-nail interaction
2016-09-15
山西省煤层气联合研究基金资助项目(2012012003); 国家自然科学基金资助项目(51408558)
李建军(1969-), 男, 副教授, 硕士生导师, 博士, 主要从事岩土工程和煤层气的研究.
1673-3193(2017)02-0133-07
TU476
A
10.3969/j.issn.1673-3193.2017.02.007
