一种SWAT模型参数识别的改进方法
2017-07-29赵堃苏保林申萌萌管毓堂周静雯
赵堃+苏保林+申萌萌+管毓堂+周静雯

摘要:参数的敏感性分析和不确定性分析是分布式水文模型构建的先决条件。在辽河流域建立SWAT模型,利用SWAT-CUP中的SUFI-2算法进行参数的率定,在此基础上提出一种更为简便的参数识别方法。将研究区域辽河干流的主要支流分别进行参数识别,再将SWAT-CUP中率定的最佳参数的从TXINOUT文件中提取出来,分别覆盖到SWAT模型中各对应支流子流域的TXINOUT文件中,即可得到按主要支流经过参数识别后的SWAT模型,避免了SWAT-CUP调参工具涉及众多子流域导致参数识别过于复杂的问题。结果表明,辽河干流主要支流招苏台河、清河、柴河等子流域主要水文断面率定期的平均纳什效率系数分别为0.60、0.65、0.68,验证期分别为0.60、0.72、0.77,参数率定的结果相对于全局调参有较大的改进。采用本文提出的参数识别方法,可以解决SWAT-CUP全局调参时上下游断面结果难以同时匹配或伪匹配的问题,又可以避免分区参数识别时对不同子流域的土地利用类型、土壤类型以及坡度等参数的繁琐设定,同时降低了SWAT模型手动调参的复杂程度,可较好地应用到SWAT模型参数识别过程中。
关键词:敏感性分析;不确定性分析;SWAT模型;SWAT-CUP;参数识别
中图分类号:P332 文献标识码:A 文章编号:1672-1683(2017)04-0049-05
Abstract:The sensitivity analysis and uncertainty analysis of model parameters are the preconditions for the construction of distributed hydrological model.In this study,a SWAT model was established for the Liao River Basin,and the parameters were calibrated via the SUFI-2 algorithm in SWAT-CUP.On this basis,a more convenient parameter identification method was proposed.The parameters of the main tributaries of Liao River were identified first,and then the best parameters calibrated from SWAT-CUP were applied to the TXINOUT files of each corresponding tributary sub-basin in the SWAT model.Thus a calibrated SWAT model was established with its parameters identified according to the main tributaries.This avoided the complexity of parameter identification in the original procedures of SWAT-CUP tool.The results showed that the average Nash coefficients at main hydrological stations in Zhaosutai River,Qing River,and Chai River were 0.60,0.65,and 0.68 respectively in the calibration period,and 0.60,0.72,and 0.77 respectively in the validation period.The results of parameter calibration improved much compared with the global parameter calibration.This parameter identification method can solve the problem that SWAT-CUP global calibration results cannot match both the upstream and downstream sections or the problem of pseudo match.It can avoid complicated parameter settings for land use type,soil texture,and slope of different sub-basins.At the same time,it can reduce the complexity of manual adjustment of SWAT model parameters.The method can be applied well to the process of SWAT model parameter identification.
Key words:sensitivity analysis;uncertainty analysis;SWAT model;SWAT-CUP;parameter identification
1 研究背景
參数的敏感性分析和不确定性分析是分布式水文模型模拟时不可避免的重要环节。分布式水文模型在拥有众多优点的同时,也面临着参数过多难以率定的问题[1]。以SWAT模型为例,SWAT(soil and water assessment tool)模型是20世纪90年代美国农业部农业研究中心(USDA-ARS)开发的流域尺度、时间连续、基于过程的半分布式机理模型[2],它作为一个典型的分布式水文模型,在国内外的应用非常广泛。目前SWAT模型参数的优选工作可分为人工调整和自动调整[3]。人工调整即手动校准参数,参数的取值受水文工作者的主观影响大,参数的率定过程比较复杂,需要耗费大量的时间和精力,因此不能较好的应用到SWAT模型的参数识别过程中。自动调整主要是应用SWAT-CUP对模型输出的结果进行参数的自动率定、敏感性分析和不确定性分析,但是SWAT-CUP在全局调参时结果难以同时匹配,并且在分区参数识别时对不同子流域的土地利用类型、土壤类型以及坡度等参数需要进行一系列繁琐的设定。本文在此基础上,提出一种简便的参数识别方法,即将研究区域干流的主要支流分别进行参数识别,并将SWAT-CUP中率定的最佳参数的从TXINOUT文件中提取出来,分别覆盖到SWAT模型中各对应支流的子流域的TXINOUT文件中,即可得到按主要支流进行参数识别后的SWAT模型。该方法可较好地应用到SWAT模型参数识别过程中。
2 原理與方法
2.1 SWAT模型原理
SWAT模型是应用较为广泛的分布式水文模型[4-6]。SWAT模型是在水文循环模拟的基础上,将参与和影响水文循环各要素的变化过程进行模拟和分析的一种基于流域尺度的分布式水文模型[7]。模型的物理基础较强,能在综合考虑期限、土壤以及土地利用等一系列因素的基础上灵活模拟各种复杂情景。模型主要由子流域、水库演算和河道演算3个模块组成[2]。根据水文循环原理,模型计算水量平衡基本表达式如下:
2.2 模型参数识别方法
SWAT-CUP是一种专门为 SWAT模型参数率定而开发的计算机程序[8]。该程序将GLUE,ParaSol,SUFI2,MCMC和PSO程序与SWAT模型联系起来,主要用于模型敏感性、参数不确定性分析及参数率定和验证[3]。本方法用其中的SUFI2方法进行参数的自动率定。
SUFI2算法是一种参数估计的最优化方法[9-10]。SUFI2[11]算法通过拉丁超立方随机采样法(Latin-Hypercube simulations)随机生成一组参数代入 SWAT 中进行目标函数的计算。模拟数据包含95%的不确定性因素,排除了5%的极差模拟条件。
本方法首先将研究区域内的干流划分为若干主要支流,根据初步建立的SWAT模型找出每条支流所对应的子流域,将这些支流率定期的水量等信息输入到SWAT-CUP中,选取对干流影响较大的7~10个参数进行自动率定。此时在SWAT-CUP的输出文件TXINOUT中的参数是最后一次率定的结果,但可能不是最佳参数的率定结果。要将参数设置为最后一次迭代的最优值,还要回到SWAT-CUP程序中,在Summary_Stat.txt中找到最佳模拟结果的序号,在 SUFI2_swEdit.txt 文件中,设置起始和结束模拟序号为最佳模拟的序号,在 Calibration 下,先运行SUFI2_run.bat,再运行SUFI2_post.bat,此时得到的输出文件即为最佳模拟结果。参数率定结束之后,将最佳模拟结果的TXINOUT文件分别覆盖到SWAT模型中各对应支流的子流域的TXINOUT文件中,即可得到按主要支流进行参数识别后的SWAT模型。
3 应用
3.1 研究区概况
选择辽河流域铁岭段作为研究区域,面积为1.7万km2。辽河位于中国东北地区南部,是中国东北地区南部的最大河流,是中国七大江河之一。南濒渤海与黄海,西南与内蒙内陆河和河北海滦河流域相邻,北与松花江流域毗连。辽河流域大部分地区属温带半湿润半干旱的季风气候。年降水量约为350~1000 mm,年径流量为89亿m3地多于平原,从东南向西北递减。流域年降水量的65%集中于每年的4月-9月。辽河流域年平均气温约在4 ℃~9 ℃间,全年气温1月份最低,平均在-9 ℃~-18 ℃之间,7月份温度最高,平均在21 ℃~28 ℃之间。
铁岭市地处辽宁省的北部,位于东经 123°27′-125°06′,北纬 41°59′-43°23′,属沿海省份的内陆地区。铁岭属温带季风型大陆性气候。全年日照为 2 700 h左右,年平均降雨量为700 mm左右,年平均气温6.3 ℃,最低气温-31 ℃,最高气温34.4 ℃,封冻期 150 d左右,无霜期 127~162 d。全年四季分明,雨量适中,适宜多种农作物生长。
辽河干流铁岭段从福德店入境,从珠尔山出铁岭市,铁岭段河长170.1 km。辽河主要支流有招苏台河和清河[12]。
3.2 模型的建立
建立SWAT模型所需要的数据主要包括1∶25万DEM数据、土地利用图和土壤类型分布图;铁岭市及其周边主要雨量站近10年的日降雨量等;铁岭控制单元上下游常规监测断面近10年的月水质数据等。
本研究在模型建立过程中使用了铁岭及周边地区74个雨量站和18个水文站的雨量、水文数据,根据实际情况,共划分子流域93个,用2007年-2009年的数据进行模型率定,用2010年-2011年的数据进行模型验证。具体数据及建立过程参见相关文献[13]。
3.3 模型的参数识别
3.3.1 敏感性参数的选取
根据研究区域的实际情况,结合相关文献[14-18],使用SWAT-CUP对参数的敏感性进行分析,选择径流曲线数(CN2)、土壤蒸发补偿系数(ESCO)、土壤有效含水量(SOL_AWC)等7个参数进行重点调整,参考SWAT数据库定义文件.rng获取相关参数的取值范围。主要调整参数的意义和取值范围参见表1。
3.3.2 参数率定和结果
根据初步建立的辽河流域铁岭段的SWAT模型,对模拟区域内10个流量站的水量进行全局调参,迭代次数为2 000次,模拟结果评估时间尺度为月尺度,模拟结果参见表2。
选取相关系数(R2)和纳什效率系数 (NSE)两种判断工具对模型的结果进行评价。其中R2用于评价实测值和模拟结果之间的拟合程度,其结果越接近1,说明这两者之间的线性关系越密切。NSE用来评价实测值和模拟结果之间的匹配度,其结果越接近1,说明模拟值越接近实测值,模型结果越可信。
通过计算,可以得到模拟区域内率定期的平均纳什效率系数0.59,验证期为0.57,上游率定期的平均纳什效率系数仅为0.40,验证期为0.40,结果较差。虽然中下游通江口流量站率定期的纳什效率系数达到了0.92,验证期达到了0.90,但是由于通江口属于中下游地区辽河干流上,该断面水量平衡主要受到上游各支流的影响,而上游若干水文站率定的结果较差,因此通江口水量站的水量过程并不能真正的反映流域内部的真实情况,是一种虚假的匹配。通过以上分析可以看出,全局调参的结果不理想,需要划分支流分别进行调参。
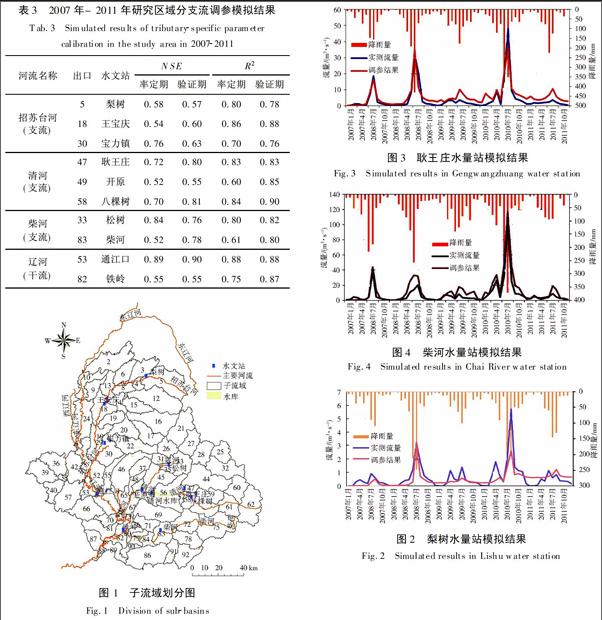
根據相关资料[19-20]以及初步建立的SWAT模型,将辽河流域铁岭段干流划分为3个主要支流,分别为招苏台河、清河和柴河,在初步建立的ArcGIS图中找到每条支流相对应子流域编号,参见图1。按照全局调参的参数设置分别对这三个支流进行参数率定,率定结果参见表3。
上述结果表明,辽河干流主要支流招苏台河、清[CM(22]河、柴河率定期的平均纳什效率系数分别为0.60、0.65、0.68,验证期分别为0.60、0.72、0.77,参数率定的结果比较好。分别选取上游的梨树流量站、中游的耿王庄流量站和下游的柴河流量站的水量数据进行比较分析,参见图2、图3、图4。
根据图表可以看出,处于招苏台支流的梨树、王宝庆流量站的模拟结果比较差,这是因为这两个水量站都位于昌图县境内,该县以种植业为主,人口众多,人类活动对河流水量的影响较大。
参数率定结束后,回到SWAT-CUP程序中,在Summary_Stat.txt中找到这三条支流最佳模拟结果的序号,在 SUFI2_swEdit.txt 文件中,设置起始和结束模拟序号为最佳模拟的序号,在 Calibration 下,先运行SUFI2_run.bat,再运行SUFI2_post.bat,得到最佳模拟结果的输出文件。将最佳模拟结果的TXINOUT分别覆盖到SWAT模型中各对应支流的子流域的TXINOUT文件中,即可得到按主要支流进行参数识别后的SWAT模型。
重新运行SWAT模型后,可以得到松树流量站和通江口流量站的参数率定结果,参见表3。根据表3可以看出这三个流量站的模拟结果比较理想。
4 结论
采用本文提出的参数识别方法,可以解决SWAT-CUP全局调参时上下游断面结果难以同时匹配或伪匹配等不合理的参数识别问题,又可以避免分区参数识别时对不同子流域的土地利用类型、土壤类型以及坡度等参数的繁琐设定,同时降低了SWAT模型手动调参的复杂程度。将此方法应用到辽河流域铁岭段已建的SWAT模型中,可以得到辽河干流主要支流招苏台河、清河、柴河率定期的平均纳什效率系数分别为0.60、0.65、0.68,验证期分别为0.60、0.72、0.77,参数率定的结果令人满意,可较好地应用到SWAT模型参数识别过程中。
参考文献(References):
[1] 王中根,夏军,刘昌明,等.分布式水文模型的参数率定及敏感性分析探讨[J].自然资源学报,2007,22(4):649-655.(WANG Zhong-gen,XIA Jun,LIU Chang-ming,et al.Comments on sensitivity analysis,calibration ofdistributed hydrological model[J].Journal of Natural Resources,2007,22(4):649-655.(in Chinese))
[2] 赖格英,吴敦银,钟业喜,等.SWAT模型的开发与应用进展[J].河海大学学报:自然科学版,2012,40(3):243-251.(LAI Ge-ying,WU Dun-yin,ZHONG Ye-xi,et al.Progress in development and applications of SWAT model[J].Journal of Hohai University:Natural Sciences,2012,40(3):243-251.(in Chinese))
[3] 帆琨,马孝义,李忠娟,等.SWAT模型参数校准方法对比研究[J].中国农村水利水电,2015(4):77-81.(FAN Kun,MA Xiao-yi,LI Zhong-juan,et al.A comparative study of the SWAT model parameter calibration models[J].China Rural Water and Hydropower,2015(4):77-81.(in Chinese))
[4] 李峰,胡铁松,赏华金.SWAT模型的原理、结构及其应用研究[J].中国农村水利水电,2008(3):24-28.(LI Feng,HU Tie-song,SHANG Hua-jin.Study on the principle,structure and application of SWAT model[J].China Rural Water and Hydropower,2008(3):24-28.(in Chinese))
[5] 康杰伟,李硕.SWAT模型运行结构与组织研究[J].地球信息科学,2007,9(5):76-82.(KANG Jie-wei,LI Shuo.Study on the running configuration of SWAT model[J].Geo-information Science,2007,9(5):76-82.(in Chinese))
[6] 温海燕,李琼芳,李鹏,等.土地利用变化对流域产水特性的影响研究[J].水电能源科学,2013,31(1):12-14,60.(WEN Hai-yan,LI Qiong-fang,LI Peng,et al.Land use change on the influence of river basin water production characteristics research[J].Water Resources and Power,2013,31(1):12-14,60.(in Chinese))
[7] 田彦杰,汪志荣,张晓晓.SWAT模型发展与应用研究进展[J].安徽农业科学,2012,40(6):3480-3483,3486.(TIAN Yan-jie,WANG Zhi-rong,ZHANG Xiao-xiao.Development and advances in application of SWAT Model[J].Journal of Anhui Agricultural Sciences,2012,40(6):3480-3483,3486.(in Chinese))
[8] Abbaspour K C.SWAT-CUP4,A User Manual[S].Dubendorf:Eawage,2011.
[9] 魏丹,刘智勇,李小冰.SWAT模型及SUFI-2算法在秃尾河上游流域径流模拟中的应用[J].干旱地区农业研究,2012,30(6):200-206.(WEI Dan,LIU Zhi-yong,LI Xiao-bing.The Application of SWAT and SUFI-2 to runoff simulation in Tuweihe (upper)watershed[J].Agriculture Research in the Arid Areas,2012,30(6):200-206.(in Chinese))
[10] 张余庆,陈昌春,杨绪红,等.基于SUFI-2算法的SWAT模型在修水流域径流模拟中的应用[J].水电能源科学,2013,31(9):24-28.(ZHANG Yu-qing,CHEN Chang-chun,YANG Xu-hong,et al.Application of SWAT model based SUFI-2 algorithm to runoff simulation in Xiushui Basin[J].Water Resources and Power,2013,31(9):24-28.(in Chinese))
[11] Abbaspour K C,Johnoson A M,Van Genuchten T.Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure[J].Vadose Zone Journal,2004,(3):1340-1352.
[12] 田麗荣.辽河流域铁岭段水质现状分析[J].地下水,2005,27(6):425-426.(TIAN Li-rong.Analysis on present water quality of tieling section in the Liao River basin[J].Groundwater,2005,27(6):425-426.(in Chinese))
[13] 申萌萌.山区丘陵地区非点源污染减排潜力研究[D].北京:北京师范大学,2014.(SHEN Meng-meng.Research of reducing emission potential of non-point source pollution in mountainous and hilly areas[D].Beijing:Beijing Normal University,2014.(in Chinese))
[14] Kannan N,White S M,Worrall F,et al.Hydrological modelling of a small catchment using SWAT-2000-Ensuring correct flow partitioning for contaminant modelling[J].Journal of Hydrology,2007,334(1-2):64-72.
[15] Wanchun L.Application of the SWAT Model for River Flow Forecasting in Sri Lanka[J].2004:1.
[16] Xue L J,Li L J,Zhang Q.Hydrological behaviour and water balance analysis for Xitiaoxi catchment of Taihu Basin[J].Water Science and Engineering,2008,1(003):44-53.
[17] Setegn S G,Srinivasan R,Dargahi B.Hydrological modelling in the Lake Tana Basin,Ethiopia using SWAT model[J].Open Hydrology Journal,2008,2:49-62.
[18] Xie X,Cui Y.Development and test of SWAT for modeling hydrological processes in irrigation districts with paddy rice[J].Journal of Hydrology,2011,396(1):61-71.
[19] 李明.辽河铁岭段水环境容量及总量分配方法研究[D].沈阳:沈阳理工大学,2012.111.(LI Ming.Study on estimation and allocation method of river water environmental capacity for Liaohe River in Tieling[D].Shenyang :Shenyang Ligong University,2012.111.(in Chinese))
[20] 霍瑾杰.铁岭市生态环境现状调查及保护措施[J].现代农业,2009 (02):47-48.(HUO Jin-jie.Tieling City survey and the present situation of the ecological environment protection[J].Modern Agriculture,2009 (02):47-48.(in Chinese))
