课标理念下数学解题能力的培养

严健强

佛山市高明区杨和镇中心小学

顾名思义，应用题的解题就是把学到的数学知识应用到学习、工作、生活、科研中解决相应的实际问题，这就是学习数学的最终目的与归宿。应用题从低级到高级，由简单到复杂，由此及彼，循序渐进，螺旋上升，覆盖小学各年级，身边处处都有数学问题。

如何进行课标理念下应用题基本技能的训练？

一、训练“三个说出”，这是最起码的技能

首先，说出条件和问题。引导学生理解一些题目中关键的字、词、句的含义。例如，红星化工厂有28吨纯硫酸，如果2吨纯硫酸要用16方水稀释。照这样计算，剩下的纯硫酸还要用水多少方？

条件：28吨 问题：剩下

2噸 16方 照这样计算 还要用水多少方？

其二，说出得数范围，让学生在计算前进行估算。例如，小华从家步行到学校，如果每分钟走40米，10分钟可以到校。实际他每分钟走了50米，只要走几分钟？（不用10分钟，超过10分钟）

其三，说出每个算式的实际意义，计算前后各说一次。例1. 小英有12元压岁钱，买课外书用去9元，还剩多少元？（12-9，12-9=3元）例2. 李师傅要做800个零件，他每天做50个，已经做了6天。（50×6，800÷50，800-50×6，800÷50-6）

二、训练“两个分析”，这是最根本的认识

第一，要教会学生分析每个数量的名称，一般在分析数量关系之前进行。例1. 三年级订《数学报》，一个月要2元钱，订一年要多少钱？[2元——单价，一年（12个月）——数量，要多少钱——总价] 例2. 自来水公司要安装1200米水管，已经安装了850米，还剩下多少米没有安装？（1200米——总量，850米——去掉的部份，剩下多少米——未安装部份）

第二，分析数量关系。有从问题想和从条件想两种方法，很多老师喜欢第一种方法，学生也容易学会。例1. 四（2）班有男生25人，比女生多5人，这个班共有学生多少人？（男生人数+女生人数=全班人数）例2. 光明电厂四月份计划烧煤900吨，实际烧煤800吨，节约了几分之几？（计划烧煤吨数-实际烧煤吨数）÷计划烧煤吨数=节约几分之几。

三、训练“两个确定”，这是正确解答的关键

确定解答步骤。在此之前，要教给学生辨清“多余条件”“重用条件”“隐蔽条件”“间接条件”等的技能。例1. 严老师买了3本教学参考书共620页，计划八月份看完，平均每天要看多少页？（3本——多余条件，八月份——隐蔽条件，即31天） 例2. 希望工程小学今年植树节种树2006棵，比去年多种200棵，两年共种树多少棵？（2006棵在列综合式中“重用”，“比去年多种200棵，没有直接给出，是间接条件）。确定先算什么，再算什么，然后算什么，分步列式解答还是列综合式解答。

确定列式方式。是一种选择正确算式的训练。例：学校藏书室有科普书200本，借给五年级5个班，每班30本，还剩多少本？[200÷5-30，200-30×5，（200-30）÷6]

四、训练“三个完成”，这是突破难点

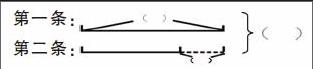
教学应用题，为了帮助学生理解题意，找出数量关系，往往采用画实物图，或画线段图，从中突破难点。我们可以训练学生完成图示，加深认识。例如图：有两条电线，第一条长85米，第二条比第一条短28米。两条电线共长多少米？

现行小学数学课标实验教材，许多题目采用题组形式出现，便于学生正迁移解决问题，分散了难点。教学时，老师要着重完成比较一组题的不同部份。例如：

1. 徒弟做了36个零件，师傅做了72个零件，两人一共做了多少个零件？

2. 徒弟做了36个零件，师傅做的个数是徒弟的2倍，师傅做了多少个零件？

3. 徒弟做了36个零件，师傅做的个数是徒弟的2倍，两人一共做了多少个零件？

有许多应用题，一道题连续出现二、三个问题，这也是为了分散难点，可是有的学生往往没有解答完。老师要提示和训练学生完成连续解答每个问题。例如：一项工程，甲队独做需要8天完成，乙队独做需要12天完成。那么，甲乙队合做一天完成全工程的几分之几？合做5天做了全工程的几分之几？两队合做7天，还剩几分之几？

进行应用题解题基本技能训练，方式方法灵活多样，在教学实践中善于积累许多行之有效的经验，提高学生应用题的解题能力。实践表明，这样的训练是数学科教学贯彻素质教育的一条途径，是学法指导的一种形式，能促进学生学习数学的兴趣，提高数学教学的效率。

责任编辑 龙建刚