仅食饵有病的生态传染病模型的全局性态分析
2017-07-24刘俊利张太雷西安工程大学理学院陕西西安70048长安大学理学院陕西西安70064
刘俊利, 贾 滢, 张太雷(.西安工程大学 理学院,陕西 西安 70048; .长安大学 理学院,陕西 西安 70064)
仅食饵有病的生态传染病模型的全局性态分析
刘俊利1, 贾 滢1, 张太雷2
(1.西安工程大学 理学院,陕西 西安 710048; 2.长安大学 理学院,陕西 西安 710064)
文章研究了仅食饵有病的捕食-食饵传染病模型的全局动力学行为。根据Routh-Hurwitz判据、Lyapunov函数和LaSalle不变集原理,得到无病平衡点、边界平衡点与正平衡点的局部和全局渐近稳定性。数值模拟给出了正平衡点处Hopf分支的存在性。
捕食-食饵模型;平衡点;全局稳定性;Hopf分支
近年来,以Lotka和Volterra为代表的种群动力学和以Kermack及Mckendrick为代表的流行病动力学已经有了相当大的发展,而将两者结合建立生态传染病模型则更具有实际意义。其中,食饵有病的生态传染病模型引起了许多学者的关注,并取得了一些研究结果[1-7]。
文献[8-9]相继研究了两类疾病仅在食饵中传播的捕食者-食饵模型,且都给出了正平衡点处分支的存在性。文献[8]考虑了捕食者的消化时滞,建立了时滞微分方程模型;文献[9]中的捕食-食饵模型采用具有比率依赖的Michaelis-Menten型功能反应函数。文献[10]研究了具有Holling Ⅱ功能反应、脉冲比例收获和脉冲常数投放的食饵两捕食者系统的分支与混沌。
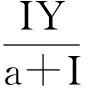
基于以上假设,建立如下捕食-被捕食模型:
(1)
为了研究方便,做以下变换:
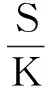
同时用t代替ω,则模型(1)可化为:
(2)
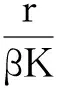
模型(2)的初始条件为:
={(s,i,y)∈R3:s≥0,i≥0,y≥0}。
易证,模型(2)的解总存在且为正。
模型(2)总存在种群消亡平衡点E0(0,0,0)和无病平衡点E1(1,0,0)。
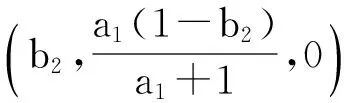
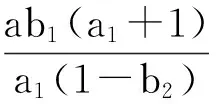
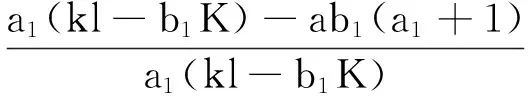
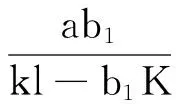
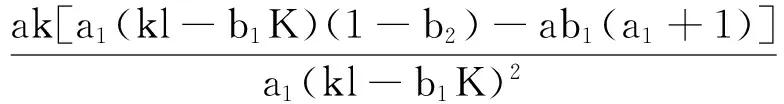
由文献[9]中引理2.1得到模型(2)的解的有界性。
引理1 假设系统的初始条件满足s0+i0≥1,下列结论有且仅有一个成立。
(1) 对任意t≥0,有s(t)+i(t)≥1,因此(s(t),i(t),y(t))→E1(1,0,0)。
(2) 存在t1>0,当t>t1时,有s(t)+i(t)<1。
因此,若s0+i0<1,则对任意t≥0,有
s(t)+i(t)<1。
由引理1易得系统的正向不变集为:
1 平衡点的稳定性
首先研究平衡点的局部稳定性。
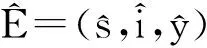
(3)
在E0(0,0,0)处,特征方程(3)变为:
(λ-a1)(λ+b1)(λ+b2)=0。
对应的特征根为λ1=-b1,λ2=-b2,λ3=a1>0,则E0不稳定。
在E1(1,0,0)处,特征方程(3) 变为:
(λ+a1)(λ+b1)(λ+b2-1)=0。
显然,当b2>1时,上述特征方程的特征根均具有负实部,E1局部渐近稳定;当b2<1时,有正的特征根λ=1-b2,则E1不稳定。
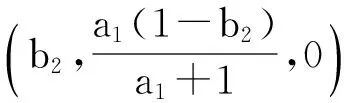
(λ-e1)(λ2+e2λ+e3)=0
(4)
其中

e2=a1b2λ+a1b2(1-b2);
e3=a1b2(1-b2)。
记方程(4)的特征根为λ1、λ2、λ3,则有:

λ2+λ3=-a1b2,
λ2λ3=a1b2(1-b2)。
当b2<1且a1(1-b2)(kl-b1K)-ab1(a1+1)<0时,易知方程(4)的3个特征根均具有负实部,即E2是局部渐近稳定的。
当b2<1且a1(1-b2)(kl-b1K)-ab1(a1+1)>0时,λ1>0,因此E2不稳定。
综上所述,有如下定理。
定理1 对模型(1)而言,有以下结论。
(1)E0(0,0,0)为不稳定的平衡点。
(2) 当b2>1时,E1(1,0,0)局部渐近稳定;当b2<1时,E1(1,0,0)不稳定。
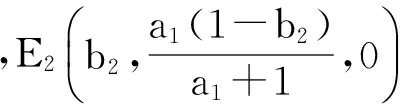
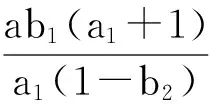
由结论(3)得,E*(s*,i*,y*)处的特征方程为:
λ3+Q1λ2+Q2λ+Q3=0,
其中


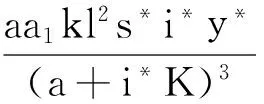
由Routh-Hurwitz判据知,E*(s*,i*,y*)局部渐近稳定的充分必要条件是Q1>0,Q3>0,Q1Q2-Q3>0。由Q1、Q2、Q3的表达式知Q3>0,而Q1、Q2的符号不确定。因此,E*(s*,i*,y*)的局部稳定性不能确定。由第2部分的数值模拟可以看到,在正平衡点E*(s*,i*,y*)处会出现Hopf分支现象。
下面研究平衡点的全局稳定性。
定理2 当b2≥1时,无病平衡点E1(1,0,0)是全局渐近稳定的。
证明 令
考虑如下Liapunov函数:
L1=s-1-lns+i。
由模型(2)得:
L1′=-a1(1-s)(1-s-i)+(1-b2)i-
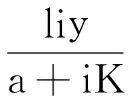
当b2≥1时,L1′≤0且L1′=0当且仅当{(s,i)|(s,i)=(1,0)}。
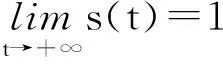
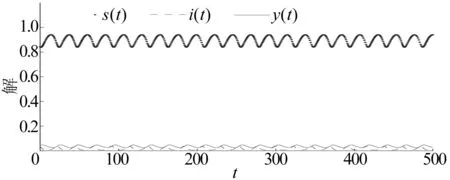
定理3 若b2<1且kl 证明 由模型(2)的第3式得: 由模型(2),当t>t1时,有 (5) 和 (6) 考虑辅助方程组: (7) 易知方程组(7)有一个正平衡点: 且(x*,y*)是全局渐近稳定的。因此,由比较原理得: 再考虑辅助方程组: (8) 方程组(8)有一个正平衡点: 且(u*,v*)是全局渐近稳定的。根据比较原理得: 由η的任意性,有 因此,当t→∞时,有 下面给出正平衡点E*全局渐近稳定的一个充分条件。 定理4 若s+s*≥1,且满足如下条件:当 证明 令 则 因为 +(a1+1)b2i*-(a1+1)si*+ 所以 故在题设条件下得L2′≤0,即E*全局渐近稳定。 在第1节中,正平衡点的局部稳定性没有得到解决;本节从数值上证明:在一定情形下,正平衡点处会出现Hopf分支现象。 图1 模型(2)的解关于时间t的曲线 本文讨论了一类仅食饵有病的生态传染病模型的平衡点的稳定性和Hopf分支的存在性。通过分析特征方程,由Routh-Hurwitz判据讨论了无病平衡点和边界平衡点的局部稳定性;利用Lyapunov函数和比较原理证明了无病平衡点、边界平衡点和正平衡点的全局稳定性。数值模拟证明了正平衡点处Hopf分支的存在性。 [1] 宋新宇,肖燕妮,陈兰荪.具有时滞的生态流行病模型的稳定性和Hopf分支[J].数学物理学报,2005,25(1):57-66. [2] 韩丽涛.一类食饵中存在疾病的捕食系统的SIS传染病模型[J].工程数学学报,2007,24(1):71-78. [3] 黄友霞,王辉,苏丹丹.食饵有病的生态-流行病模型的稳定性研究[J].生物数学学报,2008,23(1):132-138. [4] 赵丽萍,李自珍,王文婷,等.一类疾病垂直感染的生态-流行病模型的动力学研究[J].兰州大学学报(自然科学版),2009,45(4):127-132. [5] XU R,ZHANG S H.Modelling and analysis of a delayed predator-prey model with disease in the predator[J].Applied Mathematics and Computation,2013,224:372-386. [6] 陈安宁,许万银.一类食饵染病且垂直传染的生态流行病扩散模型的整体性态[J].生物数学学报,2014,29(4):718-726. [7] 袁媛,段复建.一类捕食者具有阶段结构的时滞捕食模型的稳定性分析[J].合肥工业大学学报(自然科学版),2015,38(1):140-144. [8] XIAO Y N,CHEN L S.Modeling and analysis of a predator-prey model with disease in the prey[J].Mathematical Biosciences,2001,171(l):59-82. [9] XIAO Y N,CHEN L S.A ratio-dependent predator-prey model with disease in the prey[J].Applied Mathematics and Computation,2002,131:397-414. [10] 吴兴杰,黄文韬,马忠军.具功能反应的脉冲食饵两捕食者系统的分支与混沌[J].合肥工业大学学报(自然科学版),2009,32(2):256-261. [11] LIU W M.Criterion of Hopf bifurcation without using eigenvalues[J].Journal of Mathematical Analysis and Applications,1994,182:250-256. (责任编辑 朱晓临) Global behavior of an eco-epidemic model with disease in the prey LIU Junli1, JIA Ying1, ZHANG Tailei2 The global behavior of a predator-prey epidemic model with disease in the prey is studied. Based on the Routh-Hurwitz criteria, Lyapunov function and LaSalle invariant set principle, local and global asymptotic stability of the disease-free equilibrium, boundary equilibria and positive equilibrium are derived. The existence of Hopf bifurcation at the positive equilibrium is proved by numerical simulation. predator-prey model; equilibrium; global stability; Hopf bifurcation 2016-01-22; 2016-05-17 国家自然科学基金资助项目(11101323);陕西省自然科学基础研究计划资助项目(2014JQ1038;2014JQ1018);陕西省教育厅专项科研计划资助项目(16JK1331)和西安工程大学研究生创新基金资助项目(CX201608) 刘俊利(1981-),女,河南濮阳人,博士,西安工程大学副教授,硕士生导师; 张太雷(1980-),男,湖北松滋人,博士,长安大学教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.06.026 O175.13 A 1003-5060(2017)06-0860-05
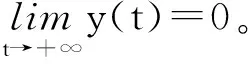
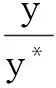
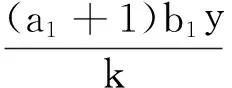
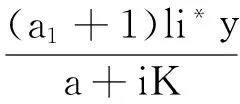
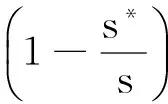
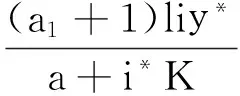
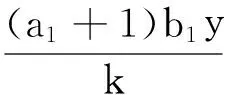
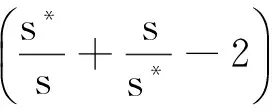
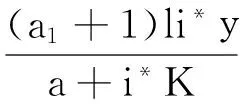
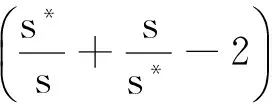
2 数值模拟
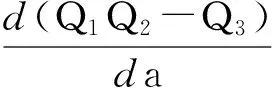
3 结 论
(1.School of Science, Xi’an Polytechnic University, Xi’an 710048, China; 2.School of Science, Chang’an University, Xi’an 710064, China)
