基于粒子的水沸腾模拟

刘洋洋, 朱晓临, 梁欣鑫, 范承凯(合肥工业大学 数学学院,安徽 合肥 230009)

基于粒子的水沸腾模拟

刘洋洋, 朱晓临, 梁欣鑫, 范承凯
(合肥工业大学 数学学院,安徽 合肥 230009)

近年来,定位流体(position based fluids,PBF)方法以其高效的计算速率和真实的模拟效果成为模拟大场景流体运动的主流方法。文章基于PBF方法使用少量的流体粒子模拟水的沸腾场景。首先采用流体粒子作为热量传输的媒介,通过SPH方法中的核函数理论处理模型中的热传导,使得模拟区域的热量分布更连续,相比于传统的以网格作为热量传输媒介的加热方式,模拟效果更好;其次在流体粒子模型的属性计算中引入粒子效果精度,加快模型计算速度。实验结果验证了该模型具有更好的模拟效果及稳定性。

流体模拟;沸腾；定位流体方法;气泡

自然现象的流体中,水流的场景模拟以其丰富的视觉感在电影特效和游戏制作里具有重要的应用价值。目前流体模拟中较流行的2种方法分别是欧拉网格法和拉格朗日粒子法。欧拉网格法是固定在模拟对象所处的空间上的模拟对象在固定网格单元上运动。文献[1]使用交错网格开创了一种稳定性较差的三维水流模拟方法; 文献[2]模拟三维流体运动时介绍了一种无条件稳定的方法来近似求解流体运动方程,该方法结合了半拉格朗日方法和隐式求解方法,因此可以得到实时稳定的模拟结果,但是半拉格朗日方法却会造成大量数值耗散而导致一些典型的“漩涡”效果消失太快。这一缺点后来被文献[3]采用高阶插值和涡流限制解决。尽管如此,作为基于网格的模拟方法主要的局限性仍是普遍的计算复杂度太高。拉格朗日粒子法是通过追踪一系列任意分布的“节点”来求解具有各种边界条件的积分方程或偏微分方程组,从而得到精确稳定的数值解。光滑粒子动力学方法(smoothed particle hydrodynamics,SPH)是最早提出的一种粒子方法,文献[4-5]将该方法应用到连续固体力学和流体力学中,并将SPH方法解释为核函数法,成功模拟了流场中的激波强间断现象。文献[6]构建了一种可以对流体的自由表面交互模拟的SPH模型;此后,SPH方法才正式广泛应用于模拟不可压缩流体以及多相流体模拟。然而由于SPH本身精度和稳定性等原因,流体模拟的效果很一般。文献[7]提出了一种新颖的基于定位动态学的流体模拟方法(position based dynamics，PBD),通过物体运动的限制方程来修正物体的位置,这种方式的运算效率很高,模拟流体的运动也具有很真实的动态感。文献[8]结合SPH方法和定位动态学方法提出了定位流体方法(position based fluids，PBF),通过粒子密度限制方程来校正位置,模型中人工添加的压力项很好地避免了粒子小范围飞溅或聚集的问题,模拟效果很好,适用于大规模的场景模拟。

模拟流体内部的气泡运动同样是流体模拟中的一个重要组成部分,而气泡模拟中常用的方法有volume of fluids(VOF)[9]和水平集方法(level set method)[10-11],它们同属于基于欧拉网格下构造的界面捕获类方法,并且都用一个标量函数来描述界面的几何特征,可以很好地处理拓扑结构。本文采用粒子方法来模拟流体内部气泡的运动过程,气泡粒子在上升中逐渐变大并融合附近的气泡粒子。这种气泡模拟方式无须考虑气泡形状的变化,可以加速模型的计算效率。

1 定位流体简介

模拟不可压缩流体的关键是如何在快速的模拟计算条件下保持流体对象的某一物理量(压强、密度或者能量等)守恒,例如N-S(Navier-Stokes)方程是通过控制流体运动时的动量和能量守恒来精确描述流体运动,同时它也是流体模拟的物理模型中典型的控制方程,但是其偏微分方程组的数值解法复杂而且耗时,难以保证实时模拟的要求。文献[8]提出的定位动态学方法通过控制流体粒子运动时的密度保持不变,先预测模拟对象的位置,再通过数次位置的迭代校正,最终满足给定的密度限制方程。

在PBF方法的粒子模型中,密度限制要求模拟中的粒子密度值保持不变。首先令Ci(p)=ρi/ρ0-1,其中，ρ0为粒子的静止密度；粒子i的密度计算公式为：

其中,h为支集半径，粒子i的支集半径表示以粒子i的坐标为中心,h为半径的一个球形空间范围;p=[p1,p2,…,pn]T,pj(j=1,2,…,n)表示粒子i支集半径内其他粒子的位置;mj为粒子j的质量;W1(pi-pj,h)为核函数。在下面的计算过程中用到的核函数W1、W2、W3参考文献[7]。然后确定粒子的位置修正值Δp,新位置满足如下密度限制方程:

Ci(p+Δp)=0

(1)

显然Δp变化最快的方向和函数梯度Ci(p)的方向一致,因此可以确定一个标量λi满足：

(2)

(1)式的泰勒一阶近似为:

Ci(p+Δp)≈Ci(p)+Ci(p)Δp=0

(3)

将(2)式代入(3)式,解得:

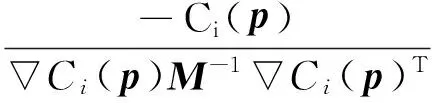
(4)

其中，M=diag(m1,m2,…,mn)表示邻近粒子的质量构成的对角矩阵。为了避免计算(4)式时分母为0,在分母上增加一个调节参数ε(ε>0),(4)式改为:

(5)

将(5)式代入(2)式得:

为了使粒子的新位置更快地满足密度限制方程,可以把支集半径内的粒子密度限制系数λj加入到粒子的位置更新中,同时引入一个非负的人工压力项s以避免粒子的“聚簇”现象,其数值参数同文献[8]。

综上,Δp的最终计算如下:

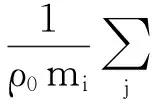
(6)

对(6)式数次迭代后,新位置的粒子在给定的误差范围内满足密度限制方程,同时加入的人工压力项使得表面的模拟效果更自然。

为了减小计算中数值耗散对模拟的影响,给每个粒子加入涡流限制(vorticity confinement),粒子添加的旋转力形式如下:

ωi=W3(pi-pj,h),

vij=vj-vi,η=|ωi|,N=,

(7)

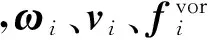
最后给每个粒子添加适当的黏性力,以保证连续运动的实时效果:

(8)

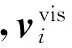
2 模型框架

因为本文的模拟场景是水逐渐加热至沸腾产生气泡,所以本文模型包括热传导模型和粒子模型,其中粒子模型有流体粒子模型和气泡粒子模型。流体粒子额外加入一个温度属性T,当流体粒子温度达到极大值时,流体粒子分解形成气体粒子,在压力作用下气体粒子快速上升并在液体表面处“破裂消失”。

2.1 热传导模型

本文模型将水槽流体粒子模拟区域网格化,每个网格只有一个温度属性T(x,y,z),初始值为20,最大值为100;然后虚拟一个在水槽底面网格上的热源区域Ω(X±φ，0，Z±φ),其中(X,0,Z)为热源的中心位置；φ和φ分别控制热源在X和Z方向上的加热范围。水槽内部网格的热量传输遵从热传递原理:

=αΔ2T

(9)

其中,α为一个和热量传输速率相关的常量,本文取α=0.1。

热传导粒子模型中的受热对象是粒子,热量也是通过粒子的运动进行扩散。首先假定与受热区域直接接触的流体粒子温度与热源温度相同,然后通过SPH方法中的光滑核函数可以近似得到区域内任意位置的热量大小,将传统的小立方体表示的离散型温度分布转化为空间连续型的温度分布。

使用SPH方法近似后,(9)式变为：

(10)

其中，α′为一个和热传导相关的调节参数；xi、xj分别为粒子i和粒子j的空间位置。考虑到SPH方法自身存在的数值耗散以及在边界处计算精度不足等引起的热量丢失,将(10)式最终改为如下形式:

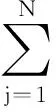
(11)

假设模拟区域内粒子的总数量为M,由(11)式可得粒子模型热传导方法的计算复杂度为O(M)。

在真实的水沸腾场景中,水分子的热量直接影响其内能,进而使得水分子剧烈运动;而在流体沸腾的模型中,同样也要设置流体粒子的温度对其速度值的增幅。本文使用的速度增幅为:

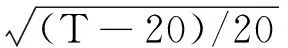
(12)

2.2 气泡粒子模型

本文的气泡模拟包括气泡生成、气泡上升、气泡破碎的模拟。在气泡上升的过程中,其体积逐渐增加,碰撞多个气泡融合生成一个新的大气泡粒子,气泡在液体表面“爆炸”后推动附近的流体粒子,产生液面沸腾效果。

2.2.1 气泡生成

在加热过程中,水由于溶解度的降低会在受热区域逐渐析出空气形成气泡,因此模型中受热网格的温度在达到最大温度后,与之相接触的流体粒子会在下一时刻“汽化”为气泡粒子。初始生成的气泡粒子半径固定,在上升的过程中随着压力的减小逐渐变大,半径变化公式为:

r=αh+β(y-h)tb,

其中,h为气泡粒子初始生成高度;y为当前高度;tb为气泡的生命;α、β为2个调节参数,本文取值分别为0.75、0.25。

2.2.2 气泡上升

气泡粒子的运动过程同样遵循PBF方法中的密度限制方程,但其质量相对较小,因此在周围流体粒子的“压力”作用下会缓慢上升。现实中,除了流体本身的限制外,流体中的气泡在生成后的上升过程中,由于气泡区域的压力作用导致气泡粒子会靠近周围气泡数量更密集的区域,因此在气泡粒子运动的水平面上添加适当的位置校正更符合实际的模拟情形。本文气泡粒子在水平面上的运动方程如下:

(13)

其中,X+为目标气泡粒子支集半径内X坐标大于目标气泡粒子的其他粒子的数量;X-为目标气泡粒子支集半径内X坐标小于目标气泡粒子的其他粒子的数量;Z+为目标气泡粒子支集半径内Z坐标大于目标气泡粒子的其他粒子的数量;Z-为目标气泡粒子支集半径内Z坐标小于目标气泡粒子的其他粒子的数量;κ为一个调节系数,本文取κ=0.1。

2.2.3 气泡融合

2个气泡粒子融和的触发条件为粒子间距小于2个粒子半径之和,即d≤r1+r2。当一个气泡粒子需要与2个以上的粒子融合时,则出现多个粒子融合情形。粒子融合的过程严格遵从体积守恒、动量守恒。新气泡粒子的位置、半径及上升速度如下:

s=(s1+s2+…+sn)/n,

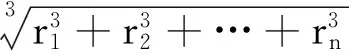
其中,融合后的气体粒子初始速度方向向上。

2.2.4 气泡破碎

气泡粒子在离开网格模拟气泡区域进入液体表面模拟区域时即开始执行气泡破碎程序。若气泡半径r≤rs(rs为人工设置的一个常量)时,则气泡直接“消失”;若气泡半径r>rs,则气泡粒子发生“爆炸”,记录爆炸粒子位置(x,ymax,z),然后以该位置为中点,kR(k为人工控制量)为半径,搜索范围内的流体粒子,对其产生“推动”效果。设流体粒子坐标为(x′,y′,z′),则其对应的分量速度增量为:

(14)

其中,λ1、λ2为调节系数,本文分别为0.2、0.3。

3 粒子效果精度

文献[12]在SPH方法的基础上引入了粒子精细度的概念,通过粒子在模拟中的位置、黏性力和压力3个因素确定粒子的精细度,并根据粒子精细度来分配粒子下一时刻的支集半径。类似地,本文加入了粒子效果精度F∈(0,1],根据粒子当前时刻的效果精度值确定下一时刻目标粒子的计算属性,其数值大小反映了粒子在模拟效果中的重要程度。

本文基于PBF粒子方法的液体粒子模型,对渲染效果有影响的因素如下: ① 液体粒子是否处于液体表面;② 液体粒子的动量。

对于因素①,当粒子处于流体表面时,粒子效果精度取值为1;其他情形和粒子的高度值成正比。然而在动态的实时模拟中,每一时间间隔内确定模拟流体的表面函数是一个很耗时的过程,因此本文直接采用高度值来判断粒子是否处于流体表面,估计流体表面略下方的粒子平均高度值为H。这种判断方式简单且计算快,适用于流体区域在高度场的运动变化幅度较小的场景,如文中模拟的流水沸腾。对于因素②,根据液体粒子的动量来计算粒子效果精度,而不直接采用粒子的速度值作为参考因素,这是考虑到以后的粒子模型的粒子种类会更丰富;没有将粒子的温度作为参考因素是因为粒子温度已经对粒子速度进行了增幅,所以选择最合适的液体粒子的动量作为计算粒子效果精度的因素。综上所述,液体粒子效果精度的计算公式为:

(15)

其中,yi为目标粒子的高度值;Ei为目标粒子的动量;Emax为目标粒子的支集半径内所有粒子动量的最大值;α+β=1,α>0，β>0。

在PBF方法模拟流体当前帧的计算全部结束后,通过最终计算出的每个粒子的效果精度值,可以动态调节粒子的支集半径和迭代次数,进而影响最终模拟的效果和计算效率。具体如下:

Ri=FPBFR,Ji=FPBFJ,

其中,Ri、Ji分别为目标粒子下一时刻计算的支集半径和迭代次数;R、J为2个定值,分别表示支集半径和迭代次数的最大值。

同样,本文的水蒸气粒子模型也对SPH方法的模拟粒子加入了粒子效果精度的属性,但是相关的影响因素不同于文献[12]。一般在烟雾模拟场景中可以影响最终效果的因素是粒子的密度和压力2个属性;密度决定了粒子对周围其他粒子的作用大小;压力决定了粒子的运动轨迹。因此,本文的水蒸气粒子效果精度计算如下:

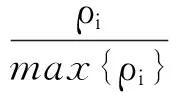
(16)

其中,max{ρi} 、max{Pi}分别为目标粒子支集半径内所有粒子的最大密度值和压力值。目标粒子的压力值计算公式如下:

其中，p(xj)为目标粒子的压强。

得到水蒸气粒子的效果精度值后就可以确定下一时刻每个粒子的支集半径，即

Ri′=FSPHR′,

其中,Ri′为目标粒子下一时刻属性计算的支集半径;R′为定值,表示支集半径的最大值。

文献[12]中的实验模拟在SPH模型中加入了粒子精细度后虽然可以提速86%，但是模拟的细节却没有得到提升。本文模型对PBF模型加入了改进的粒子精细度控制方法，在多次的调试数据模拟实验后，最终的结果是在同等模拟场景下，本文方法可以将PBF模型的计算速度提升16%～24%，同时还提高了模拟的细节效果。

4 程序步骤

本文模型的具体步骤如下：

(1) 初始化粒子模型后,在水槽底部中心区域网格进行加热。

(2) 判断流体粒子的温度T。若T≥100,则执行步骤(3);否则执行步骤(4)。

(3) 将温度达到极限的流体粒子在周围空间随机生成4个半径固定的气体粒子。

(4) 为每个粒子添加外力:

vi+Δtfext(pi)/mi→vi,

其中,fext(pi)为粒子i受到的重力。

(5) 预测下一时刻粒子的位置:

(6) 搜寻每个粒子支集半径内的所有粒子。

(7) 根据(5)式计算支集半径内每个粒子的λi。

(8) 根据(6)式计算支集半径内每个粒子的Δpi。

(10) 判断是否达到迭代步数,否则回到步骤(4)。

(11) 更新每个粒子的速度:

特别地，对气体粒子还要加入(13)式。

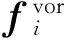
(13) 判断气泡粒子是否需要“破碎”。若是,则根据(14)式添加相关流体粒子的增量;否则执行步骤(14)。

(14) 由(12)式更新气体粒子的半径大小。

(15) 更新水槽网格的温度。

(16) 由步骤(15)的温度值及(12)式最后更新所有流体粒子的速度值。

(17) 根据流体粒子和气体粒子的位置用OpenGL进行渲染。

(18) 重复步骤(2)。

5 实验结果

本文仿真模型实验平台为Windows 7系统,程序开发的软件选用Microsoft Visual Studio 2008,三维图形的编程接口和最终的粒子渲染采用OpenGL。算法实现的硬件环境为1台Intel(R) Core(TM) i3-4130的CPU、4 G内存的PC机。为了验证本文模型的优点,本文将PBF的粒子运动程序换为传统的SPH方法,具体的模拟结果如图1所示。

图1 沸腾模型基于不同方法帧数为67的表面效果

在程序运行中通过截取图片测得图1中67帧次前后若干图的帧率，见表1所列。

由表1可见,本文的模型在基于SPH的粒子方法时模拟的平均帧率约为1.31,而PBF方法约为1.96,相比于传统的SPH方法,计算效率提高了49.6%。

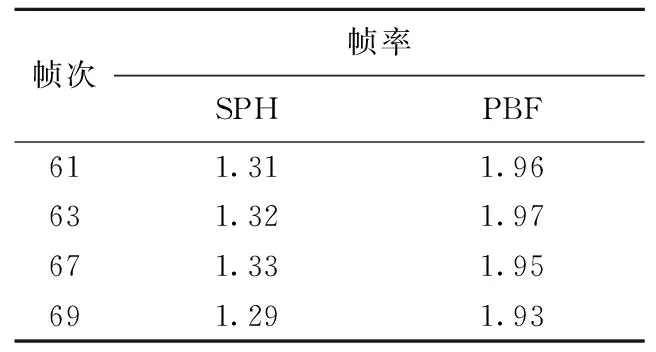
表1 SPH方法和PBF方法的帧率比较

流体沸腾模拟中,从气泡生成到气泡消失过程的气泡效果如图2所示。

图2 流体沸腾模型中的气泡模拟效果

6 结 论

本文在PBF方法的粒子框架基础上加入了气泡粒子,并通过2种不同粒子间的相互运动模拟了流体加热沸腾的场景。相比于传统的SPH方法,本文模型的计算速度更快,表面的沸腾效果更真实,模拟中加入的气泡模拟也很好地提高了模拟场景的细节。然而由于粒子模型中另一种粒子的加入使得稳定性有所降低,本文模型模拟的时间步长受到了限制,表面模拟的效果变化剧烈以致气泡粒子在即将出水时的“破裂”效果不明显,后续的研究工作将主要放在气泡模拟方面,采用新的粒子运动方法或者新的气泡粒子框架来加强流体沸腾表面的模拟。

[1] FOSTER N，METXAS D.Realistic animation of liquids.[J].Graphical Models & Image Processing，1996，58(5):204-212.

[2] STAM J.Stable fluids[J].Acm transactions on graphics，2001，1999:121-128.

[3] FEDKIW R，Stam J，Jensen H W.Visual simulation of smoke[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques.[S.l.]:ACM，2001:15-22.

[4] MONAGHAN J J.An introduction to SPH[J].Computer Physics Communications，1988，48(1):89-96.

[5] MONAGHAN J J.Why particle methods work[J].Siam Journal on Scientific & Statistical Computing，1982，3(4):422-433.

[9] HONG J M，KIM C H.Animation of bubbles in liquid [J].Computer Graphics Forum，2003，22(3):253-262.

[10] OSHER S，SETHIAN J A.Fronts propagating with curvature-dependent speed:algorithms based on hamilton-jacobi formulations[J].Journal of Computational Physics，1988，79(1):12-49.

[11] ZHENG W，YONG J H，PAUL J C.Simulation of bubbles[C]//Proceedings of the 2006 ACM SIGGRAPH/Eurographics Symposium on Computer Animation.Aire-la-Ville,Switzerland:Eurographics Association,2006:325-333.

[12] 谭诗瀚,段茗,杨红雨.非均匀粒子流体模拟[J].计算机工程与设计，2011，32(8):2760-2763.

(责任编辑 张 镅)

Boiling water simulation based on particles

LIU Yangyang, ZHU Xiaolin, LIANG Xinxin, FAN Chengkai
(School of Mathematics， Hefei University of Technology， Hefei 230009， China)

In recent years， the method of position based fluids(PBF) has become the mainstream in simulating huge scene of fluid motion for its efficient calculation and perfect effect. In this paper， the model is established to simulate the boiling water by using few of fluid particles based on PBF. In the model， the fluid particles are taken as the medium of heat conduction to handle heat exchange with the theory of kernel function in smoothed particle hydrodynamics(SPH)， which makes the distribution of heat in the simulating area more continuous and therefore obtains better simulation result compared to the traditional method using the grid as the medium of heat transference. Then the fluid particles are given a concept of precision of effect, which accelerates the computation and enhances the details on the surface. The experimental result verifies better simulation effect and stability of the model.

fluid simulation; boiling; position based fluids(PBF) method; bubble

2016-03-22；

2016-06-09

国家自然科学基金资助项目(61272024)

刘洋洋(1989-),男,安徽蚌埠人,合肥工业大学硕士生; 朱晓临(1964-),男,安徽池州人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.06.025

TP301

A

1003-5060(2017)06-0854-06