扑克牌为背景的条件概率

云南省大理市大理大学 (邮编：671003)

扑克牌为背景的条件概率

云南省大理市大理大学王雨佳王彭德(邮编：671003)

条件概率是高中人教新课标 A 版选修2-3 上的知识点，内容简单,但学生理解困难.纵观全国和各省份的近几年高考数学试卷，条件概率越来越受到命题者的青睐.诸如2012年安徽数学(理)17题，2015年北京数学(文)17题都直接或间接考查条件概率，所以条件概率在平时的教学中是一个值得研究的课题.统计与概率是一门源于生活，又用于生活的应用学科，生活中诸如抛硬币、掷骰子、抽取扑克牌的游戏，其中蕴含着丰富的概率问题，以扑克牌为背景来研究条件概率，有助于学生进一步了解条件概率.下面以扑克牌中的问题来说明条件概率的计算.

1 条件概率

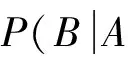
问题1从一副扑克牌中(52张，去掉大小王)，每次从中抽取一张,作不放回抽取，求第一次取到红桃的条件下,第二次取到非红桃的概率.解设Ai={第i次抽到红桃}，i=1,2.

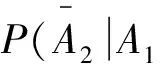
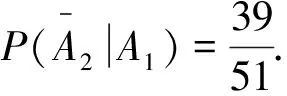
公式法，样本空间Ω中共有52个样本点，其中39张非红桃，13张红桃，

由条件概率公式得

在求条件概率时，通过条件缩减样本空间，利用定义求解，可比公式法更为简捷.

2 积事件的概率

通过条件概率的计算公式，我们可得到积事件概率的公式，即乘法公式,

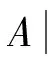
问题2从一副扑克牌中(52张，去掉大小王)，每次抽取一张进行不放回抽取，

(1)接连取两次，求第一次取到红桃，第二次取到非红桃的概率；

(2)接连取3次，求第三次才取到非红桃的概率.

解记Ai={第i次抽到的是红桃}，i=1,2，3

(1)事实上这是一个积事件的概率，而不是条件概率.

而

由乘法公式得，

(2)“第三次才取到非红桃”可表示为“第1、2次取到红桃，第3次取到非红桃”.

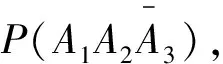
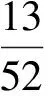
3 复杂事件的概率

在实际中有时计算一个事件的概率较为复杂，我们可将一个复杂事件的概率计算问题转化为在不同情况、不同原因或不同途径下发生的简单事件概率求和问题.

问题3从一副扑克牌(52张)中，每次取一张扑克牌，接连取两次，作不放回抽取.

(1)求第2次取到红桃的概率.

(2)已知第二次取到的是红桃，求第一次取到非红桃的概率.

解设Ai={第i次抽到红桃}，i=1,2，

(1)事实上，第2次取到红桃的可能性受到第1次取牌结果的影响，第1次可能取到红桃，也可能取到非红桃，因此第2次取到红桃可表示为两个互斥的积事件的和，则

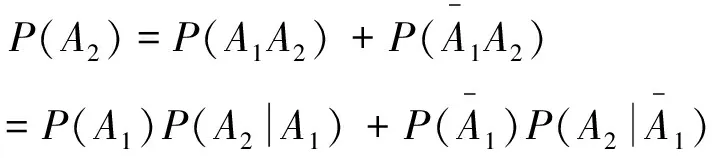
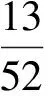
以上计算方法是大学概率论与数理统计中全概率公式的体现，它提供了计算复杂事件概率的一种有效途径，使一个复杂事件的概率计算问题化繁为简.

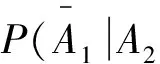
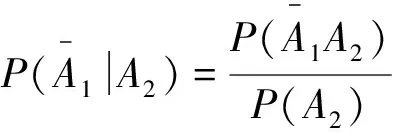
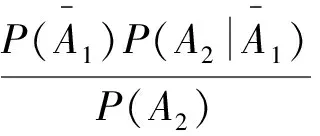
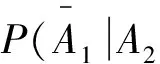
4 条件概率在分布列中的应用

离散型随机变量的概率分布列、数学期望、方差是高考数学命题的热点和重点，其中有的题型(2012年安徽数学(理)17题)也涉及到条件概率和乘法公式的应用.

问题4一副扑克牌共有13张红桃，其中3张有人头像，10张有数字，假定3张有人头像的牌是相同的，10张有数字的牌也是相同的，每次从红桃中一张一张地取牌，X表示直到取得数字牌为止所需的取牌次数，

(1)作不放回抽取，求随机变量X的分布律.

(2)每次取出一张牌后，总以一张有数字的扑克牌放回，求随机变量X的分布律.

解设Ai={第i次抽到的是有人头像的牌}，i=1,2,3,4.

(1)显然随机变量X的可能取值是1、2、3、4.

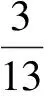
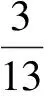
因此随机变量X的分布律为

X1234P101352651431286

(2) 随机变量X的可能取值是1、2、3、4，

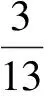
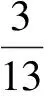
因此随机变量X的分布律为

X1234P10133316972219762197

1 王彭德.扑克牌中的概率[J].中学生数学，2003(11)

2 陈玄令.谈条件概率与积事件概率的区别[J].渤海大学学报，2004(1)

3 杨明正.对一道高考概率题的解析[J].中学数学教学，2013(1)

2017-04-12)