一道中考模拟题的错解分析 纠正和改编

山东省淄博市周村区王村中学 (邮编：255300)山东省淄博市周村区第三中学 (邮编：255300)

一道中考模拟题的错解分析 纠正和改编

山东省淄博市周村区王村中学郑学涛(邮编：255300)山东省淄博市周村区第三中学李庆生(邮编：255300)

1 问题提出

1.1 题目呈现

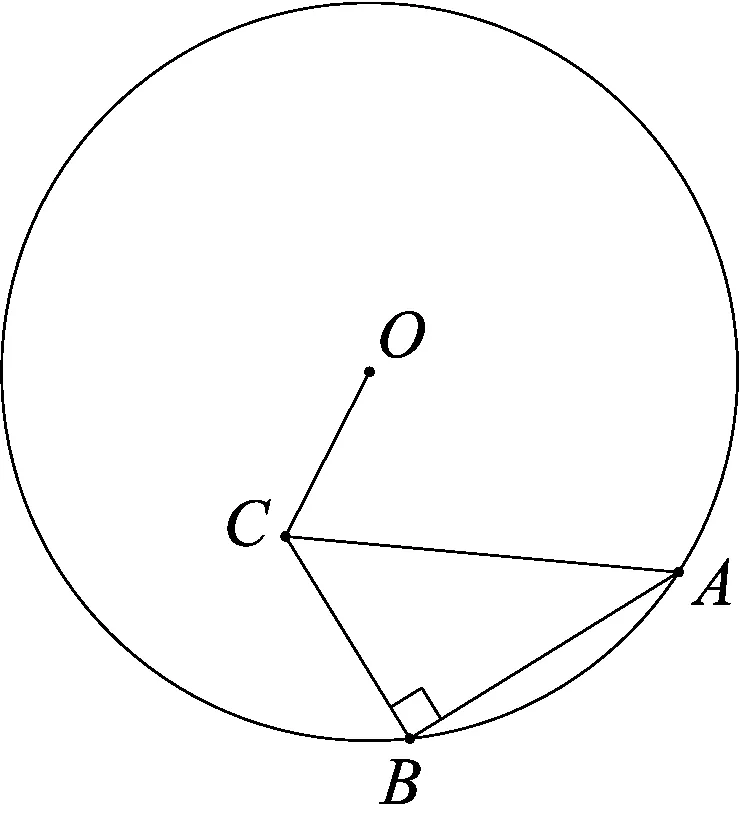
图1

1.2 选题背景

鉴于对近年来淄博市中考数学17题的难度感知，我区县在命制毕业班中考模拟试题时特选取一些设计新颖，能够体现出学生核心素养，对优秀和良好的学生具有明显区分度的题目，上题即是其中一例.

2 经验驱使 悄入误区

图2

3 知识溯源，破解迷局

在进行试题讲解前的备课时，从整体上比较了一下几种解法的优劣，觉得上面的解法比较接近学生的最近发展区，于是决定首先这种解法.但授课实际操作中，学生提出质疑：本解法中O到C点的距离最小是根据那条数学定理或者基本事实？这使笔者陷入深思和溯源，初中阶段设计线段最小值的题目有很多，但是几乎无一例外用到这样几条数学定理或事实：(1)两点之间线段最短；(2)直线外一点到直线上的所有点的线段中，垂线段最短；(3)三角形两边之和大于第三边；(4)线段长度是某个自变量的函数，最小值是通过函数的极值求得.那么上面所述线段OC最小成立的依据是哪一条呢？通过观察发现O是定点，但是O点所在的线段AD只是长度确定，位置并不确定，它会随A、B位置的变化而变化，这与(2)中直线位置确定有明显区别，且对于(2)，产生最小距离的直线上的点就是过直线外的那一点向直线作垂线之后的垂足，而本题未作垂直之前O点已赫然存在于线段AD上，在上课讲解的过程中教师未经深度思考就默认了依据(2)，这样的观点站不住脚的，那么接踵而至的问题还有如果依据不成立为什么还会解出正确结果？正确的解题方法和解题依据又是什么？上述解题方法能不能经过修改成为正确的解答？

4 解决疑惑，突出重围

图3

首先可直接排除选择(4)解决本题的可能，而要确定是依据(1)、(2)、(3)中的哪一个不妨研究一下这三个定理或事实的使用前提条件：对于(1)使用的前提是有两定点存在，那么这两定点之间的距离最小值，即是两点之间线段的长度；而对于(2)当直线外一点为定点，直线为定直线(定位置)才能利用此定理；对于(3)只有满足两线段长度固定，且第三条线段与前两条线段恰好构成三角形时才能使用，而构成的三角形两边长度固定所有情况恰好也是三角形有两个顶点的位置是固定的，第三点绕其中一个顶点作圆周运动如下图3.上述解法中只确定了O是定点就选择了依据(2)解决问题，是逻辑不严谨的.至于会得到正确答案，是因为此法虽不能证明此时OC最短，但却是OC最短时的精准图形，这一点从通过其它方法解答的过程中得到验证.因此只要在原解法上补充证明，就可以获得本题一种完整的解法，经过上述讨论还可确定在补充证明的过程中无论是选择那一条依据(除(4)外)，都要研究C点的位置.

5 完善解答 终得正果

图4

6 借题发挥 一题一课

在上述完整的解法中，所利用的定理，方法虽都是初中数学的基础知识和基本技能，但是由于本题的逻辑密度较大，转折性强，“苹果”位置太高，学生跳一跳够不着或者够着吃力，亦会体现不出题目的价值和功能，那么学生产生解题畏难情绪也是可以理解的.为让题目贴近学生的最近发展区，经过我区数学老师的进一步商讨，本题还可以有两种改编方案，初步形成一个有效的一题一课的微专题：

6.1 引导学生利用手拉手旋转相似解决本题，要把旋转的路铺好，在原题中加入利用旋转相似解题时所用得到的三角形，便于解题思路的自然生产，于是题目变为：

(1)求D、C之间的距离；

(2)求OC的最小值.

图5

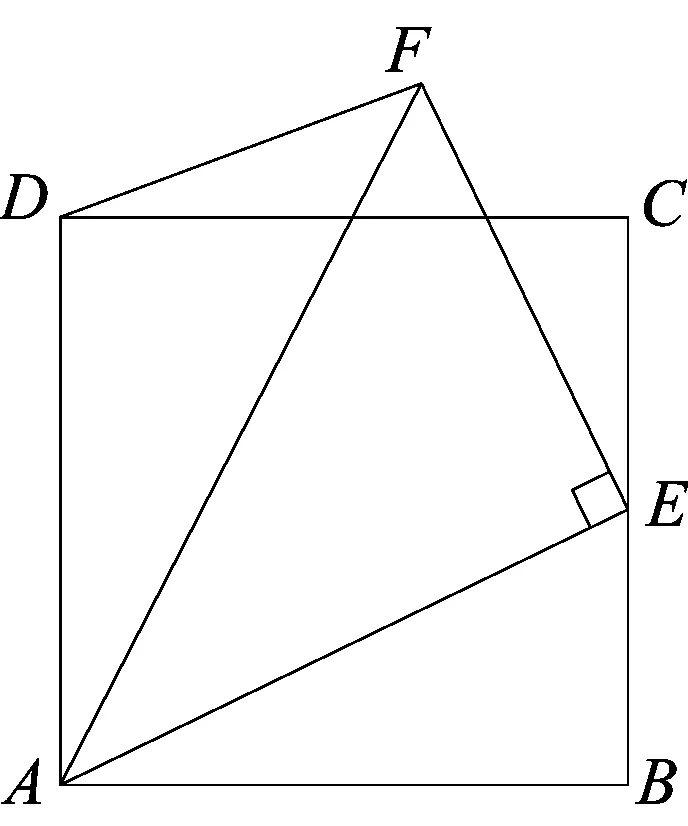
图6

(2)求线段DF的最小值；

(3)求F点经过的路径的长.

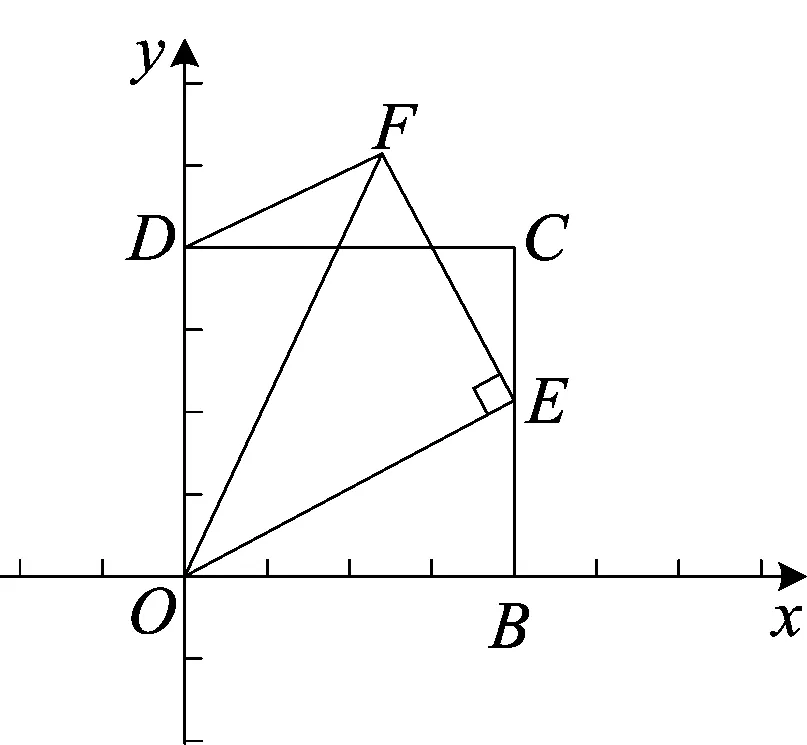
图7

7 反思解题 改善教学

高效课堂常见于课堂容量大，教师分析、讲解高位切入、云端行走，把学生的质疑、分析、修改、反思寄希望于课下或者同一节课辗转题目之间时的时间缝隙，这样的做法恰恰忽视了数学“逻辑关联、前后一致”的本质.久而久之，学生的深层次的逻辑思维能力、逻辑严谨性没有培养起来，解题总是停留在刻意模仿的阶段(形式运算阶段)，与“培养学生走上社会所需要的各种能力”的数学教育理念大相径庭.通过研究以上变式题目，使笔者深深体会到欲通过一道“孤立”的难题培养学生的各方面的能力不可小觑，教师的引导要脚踏实地，一步一个脚印，帮助学生按照知识源、方法论与解题需求关联性的远近程度排列并串联起来，方是题目解法的自然生成，也能够体现题目在培育人的逻辑思维完善性、严谨性等方面的重要价值.此外，教学时可详尽剖析各知识源的异同点和使用条件、特征与范围，以提高学生的辨析与应用能力[1].

总之，尊重教学规律、尊重学生的数学现实、尊重数学学科的特点，步步为营、环环相扣才能够释放出解题的精彩，流露出切实的学生本位，让学生获得对于他生命成长有意义的东西.

1 刘华为.从教“怎样做”到教“怎样想”[J].中学数学教学参考：中旬，2016(6):26-28

2017-04-13)