拉长知识探究过程 注重数学思维感悟
2017-07-24江苏省无锡市太湖格致中学邮编214125江苏省无锡市水秀中学邮编214125
江苏省无锡市太湖格致中学 (邮编:214125)江苏省无锡市水秀中学 (邮编:214125)
拉长知识探究过程 注重数学思维感悟
江苏省无锡市太湖格致中学陈锋(邮编:214125)江苏省无锡市水秀中学张杭嫣(邮编:214125)
1 问题提出
《义务教育数学课程标准(2011年版)》的主要变化是从“双基”到“四基”,突出了对数学“基本活动经验”的相关要求.这就要求我们教师在课堂教学中要放慢教学节奏,舍得花时间让学生体验探究知识的形成过程;让学生有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程,逐步积累活动经验、感悟数学思想、形成思维能力.下面,结合自己的教学实践,来谈一点自己对通过拉长知识探究过程促进学生数学思维能力发展的体会.
2 基于拉长知识探究过程的操作策略
2.1 概念、定义的探究——放慢节奏,感悟本质属性
李邦河院士的“数学,根本上是玩概念的”,说明概念对数学教学的重要性.在概念教学中,有部分教师只是简单直接地将有些概念、定义告知学生的,让学生强化记忆,然后就可以配合大量的课堂练习来达到巩固的效果,这样做仅仅是对概念的表层记忆,可能对学生短期记忆有效,但真的经得起时间的检验吗?学生能从本质上真正的理解这个定义吗?答案是不言而喻的.
案例1反比例函数的概念探究:
一辆汽车从南京开往上海,表示出下面式子中的数量关系.
(1)若汽车行使速度为60千米/时,汽车行使的路程S随时间t的变化而变化;
(2)若汽车先按(1)的速度行使了50千米,再按80千米/时继续行使,汽车行使的路程S随时间t的变化而变化;
(3)南京到上海的路程为300千米,时间t随速度v的变化而变化.

探究一时间t是速度v的函数吗?
对比函数定义,你认为时间t是速度v的函数吗?答案是肯定的.
探究二时间t是速度v的一次函数吗?答案显然是否定的,那么时间t和速度v之间又会存在怎样的函数关系呢?
你有什么办法能更直观地展示出时间t是如何随着速度v的变化而变化的吗?如果学生遇到困难,教师可引导函数的不同表示方法,找到表格的直观工具.

速度v(千米/时)…608090100120…时间t(小时)…5154103352…
通过表格, 再次强化函数定义,明确时间t是速度v的函数.直观感受速度增大,时间就减少的关系,体会与小学阶段所学两个量成反比这一知识点间的联系.
探究三你还能找到生活中那些量之间存在类似上题中时间t和速度v之间的函数关系呢?学生思考后举例:
(1)面积为54的矩形的长与宽;
(2)乘积为200的两个数……

效能分析在上述反比例函数概念的探究中,教师没有将学生当作接受知识的容器,而是基于学生对一次函数和正比例函数的理解.通过三个的自主探究过程,从学生对函数概念的表层理解,到认知冲突,再深入到了反比例函数本质属性的理解,可能这样的概念探究比直接告知概念学生要多花几分钟时间.但是,这三个递进式的探究过程,让学生经历对反比例函数概念的感悟和理解的过程,做到“知其然,更知其所以然”,学生可以充分理解并揭示概念的本质属性,有利于学生的思维延伸和拓展.策略引申张文质先生认为“教育是慢的艺术”,我们必须在教学过程中,放慢定义的生成过程,放大知识的形成过程,加强新知识与已有知识的联接与对比过程,注重知识的“生长点”与“延伸点”,引导学生经历猜想、操作、思考、归纳等体验性过程,并及时对方法、结论进行总结,就可以不断激发学生思维的灵感.在思考中不断提升已有的知识与结论,形成增长点,从而自然引发新的定义与结论,并能逐步使学生积累思维的活动经验落到实处.
2.2 公式、法则的探究——放手拓展,提升学习能力
数学中的公式和法则是数学对象之间的规律性反映,它们都是思维的结果,是智慧的结晶,这一特征注定了它们只能以“静态”的形式呈现在教材上.因此在公式教学时,教师的任务绝不仅仅是把“静态”的结论告诉学生,而是要引导学生探究公式与法则的由来,弄清楚这个公式是怎么产生的,能用来解决哪些问题,从而做到“举一反三,融会贯通”.
案例2多边形内角和的公式探究
上节课我们学习了三角形的内角和为180°,你知道四边形的内角和是多少吗?你是如何得到的呢?

图1
学生轻松地就能说出四边形内角和360°,并回答:因为正方形每个角是90°,所以四边形内角和360°.在辨析过这个问题后,鼓励学生继续思考,方法也不难得到:把四边形转化成三角形,如图1充分体现出了数学中化未知为已知的基本思想.但如果教师希望思维之花能继续绽放出更绚烂的花朵,就可以继续留足充分的时间给学生,他们将会回报你足够多的精彩!

图2
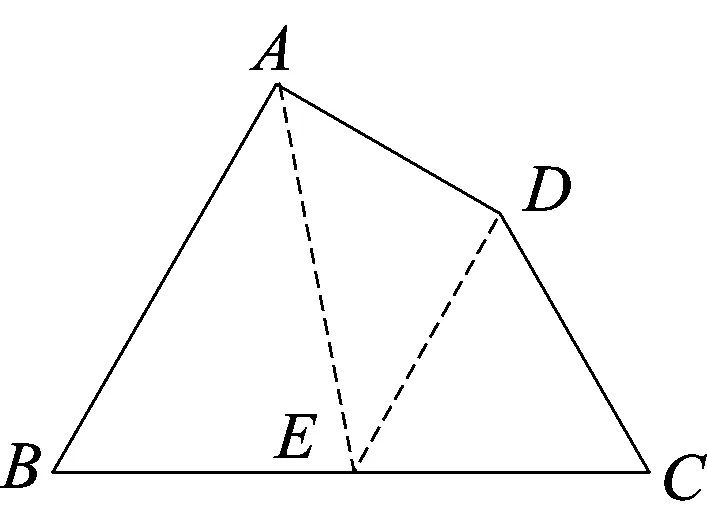
图3
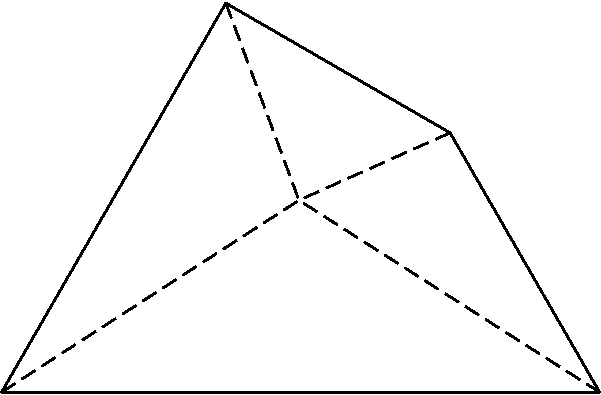
图4

图5
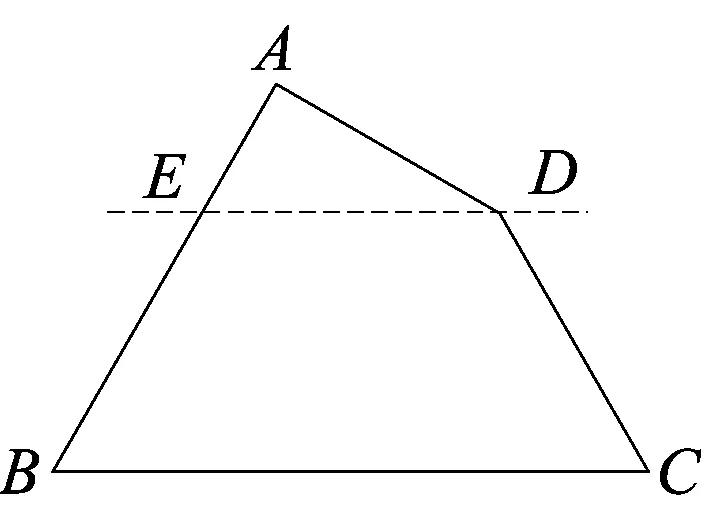
图6
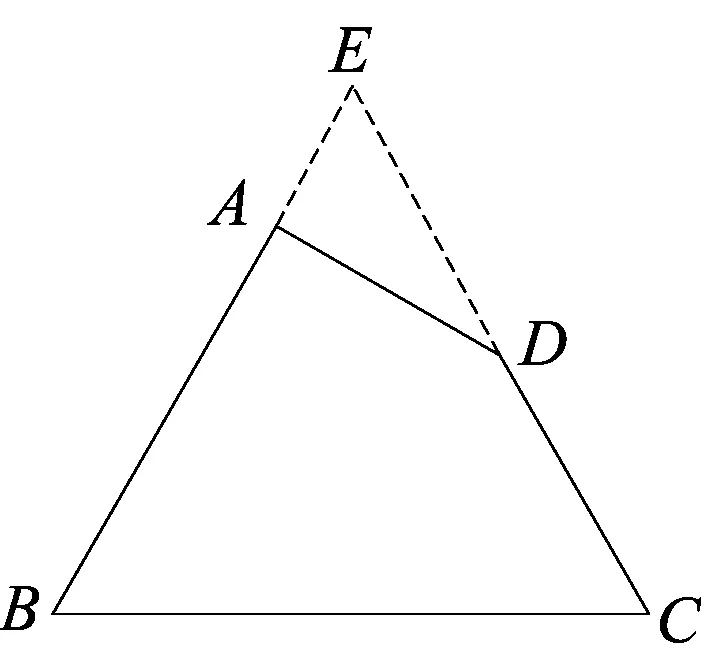
图7

图8
教师继续鼓励学生:你还能找到其他证明四边形内角和360°的方法吗?提醒学生:在自己的纸上画一画,试一试,15分钟后,我们又得到了以下的七种证明方法.
图2:连结BD并延长至E,利用外角得∠ADE=∠ABD+∠A,∠CDE=∠CBD+∠C,故∠A+∠ABC+∠C+∠ADC=∠ADE+∠CDE+∠ADC=360°.
图3:在BC上取点E,连结AE、DE,由三角形内角和180°可得∠BAD+∠B+∠C+∠ADC=180°×3-180°=360°.
同理可得,当点E取在四边形内和四边形外时,就出现了图4和图5的情况.
图6:过点D作DE∥BC,由平行的性质可得∠AED=∠B,∠EDC+∠C=180°,故∠A+∠B+∠C+∠ADC=∠A+∠AED+∠C+∠EDC+∠ADE=180°+180°=360°.
图7:延长BA、CD交于点E,故∠BAD+∠B+∠C+∠ADC=540°-180°=360°.
图8:同图7,只是在分割的过程中多转了几个弯,并出现了特殊的直角三角形与矩形.
效能分析这一探究过程花费了15分钟的时间,在经历了上述八种多边形内角和的公式探究过程,学生充分地体会到了证明四边形内角和为360°的基本思路:把未知的四边形内角和转化为已知的三角形内角和来完成求解过程.这15分钟的探究正是学生能力提升所需要的理性思维的时间与空间,在这15分钟中,学生在图1的基础上,继续深度思考,思维得以碰撞,火花得以灵现,最后有了这8种探究的成果,你还怕他们不会完成多边形的内角和的课题探究吗?你还愁他们在以后的几何学习过程中不能勇于探索吗?因此,放手让学生参与才是硬道理.有效课堂,并不在于课堂上到底讲了多少道题目,而在于学生究竟得到了多大的发展.只有放手学生参与,学生的思维才会真正尽情绽放,学生的能力才能真正大放异彩.策略引申美国华盛顿国立图书馆的墙壁上写着:我听见了,但可能忘掉;我看见了,就可能记住;我做过了,便真正理解了.由此可见,让学生亲身经历实验操作是多么重要!学生在“做数学”的氛围中主动学习数学知识,在“做”的过程中积极思考问题,引发直观猜想,并激发学生探究的欲望,学生探究的空间被无限放大.从而在“做数学”的过程提升动手能力、思维能力、发现问题、提出问题、分析问题、解决问题等各方面的能力.这样的教学,更有利于学生主动地掌握知识和形成能力.
2.3 定理、命题的探究——联系前后,培养思维能力
定理是几何基础知识重要的组成部分.定理或结论的得出是有根有据的,其推出一般都遵循着从特殊到一般的认知规律.因此,定理教学的重点与难点就是定理的推出与证明,而推理证明也恰是锻炼、培养学生逻辑推理能力的一条重要途径.在定理的探究过程中不仅仅是要使学生记住定理,更会用定理去解题,还应通过启迪和引导,使学生参与到定理的形成过程中去.
案例3三角形相似的判定定理探究
我们已经学习了(1)两角对应相等,两三角形相似;(2)两边对应成比例且夹角相等,两三角形相似,你猜测还会有什么判定方法呢?
类比相似三角形与全等三角形的关系,学生能很自然地猜想到:三边对应成比例,两三角形相似.
探究一这个结论正确吗?
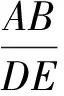
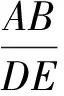
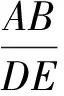
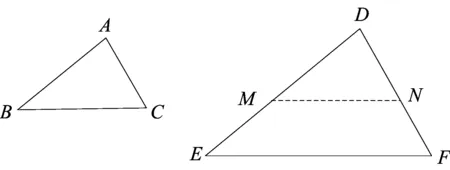
在教师适当的启发与前面相似三角形已有的学习经验的组合作用下学生会自然想到在已知和求证架起一座桥梁——构造△DMN与△ABC全等,与△DEF相似,从而自然解决问题.
效能分析在这一定理的探究过程中,教师采用了“从特殊到一般”的教学方法.基于学生已知的全等三角形的判定定理,先引导学生探究相似三角形与全等三角形的关系,再探究出相似三角形的判定定理.在操作与探究中通过合情推理先直观地猜测结论,在此基础上进一步提高要求,如何进行严密的逻辑推理最终形成定理结论呢?此时,前面两节课中已经遇到的“构造法”在教师适当的启发下进入学生的视线,轻松突破难点.这样的探究设计合乎学生已有认知经验和思维发展规律的教学流程,按学生认知结构规律进行教学,体现数学定理的形成与发展的过程,从而使学生思维能力得到有效的培养和发展.策略引申《课标(2011年版)》明确指出:“教学活动是师生积极参与、交往互动、共同发展的过程.”从中可以看出,有效教学,必须把教师的教落实到学生的学上去.课堂,如果学生不积极参与,最后又怎谈得上学习效果的提升呢?所以,教师的所有教学行为,在最后都反映在学生的学习成果上.数学教学的根本任务不仅在于向学生传授知识,更重要的是培养学生的思维能力.初中数学定理的教学,尤其是初始阶段,即使是学生很熟悉的简单定理的教学,也不能不重视定理的形成过程,要遵循特殊到一般,具体到抽象的认知规律,从而达到培养学生的数学推理能力、逻辑思维能力和创新意识,体现数学定理的形成与发展的过程的目的.3对拉长知识探究过程的操作思考
数学学习的过程,常常是看似很深奥的知识,通过努力构思前后教学活动之间的关联,加强知识体系上的前后一致,研究方法上的“基本套路”的延续强化,就可以化难为易;同时也会有些看似很浅显易懂的内容,只有深入到的“其内部”,努力使隐性的活动经验显性化,将探究中所获得的经验外显为可观察、可总结、可检测的数学学习能力,才能发现其中别有洞天.无论是化难为易还是深入浅出,只有让学生亲身经历这些“惊心动魄”的过程,这才是有效的.在探索的过程中学生认真体会着数学中发现、类比、化归、建模等基本思想,也努力感悟着猜想、试验、探索、归纳等重要的数学方法,当这些思想与方法在我们的课堂上慢慢积累,在问题解决的过程中徐徐推进时,他们从最初的朦胧状态走向明朗,再到自觉运用,这既是学习的过程,也是经验的积累.久而久之,学生学会了自觉地积累经验,学会敢想敢问从而具备勇于创新的精神,真正做到理解和掌握知识技能,体会和运用思想方法,积累和沉淀学习经验、形成和发展个性能力,变“学会”为“会学”!
数学课堂是数学思维灵动的课堂,而只有注重探究式教学,才能让学生在数学的海洋中尽情享受.在概念、命题等数学知识的教学中,只有拉长探究过程,通过数学思想、方法的渗透去“浸润”数学知识,学生才能真正理解,也只有关注概念等知识的形成过程并注重方法与思想的总结与提升,才能让学生真正感悟博大精深的数学思想.让我们静心沉浸于每节课上探究的量变,耐心等待时间、经验累积带来的质变,让我们一起静待花开的声音吧!
2017-04-05)
