利用杠杆原理解决平面几何问题

浙江省绍兴鲁迅中学 (邮编：312000)

利用杠杆原理解决平面几何问题

浙江省绍兴鲁迅中学徐耀虞关寿(邮编：312000)

阿基米德说过，“给我一个杠杆和支点，我可以撬动整个地球.”这里说的就是物理学中的杠杆原理的威力.不同学科之间的知识是可以相通的，把杠杆原理应用于某些数学问题，可以取得简洁明快的效果.本文想利用杠杆原理去解决一些平面向量问题.

1 杠杆原理

杠杆原理亦称杠杆平衡条件，即要使杠杆平衡，作用在杠杆上的两个力矩(力与力臂的乘积)大小必须相等，即：动力×动力臂=阻力×阻力臂(F1·L1=F2·L2).具体解释如下：

对于线段AB，将其视为轻质杠杆，O为支点.如果在AB的端点处分别放置质量为m1、m2的两个质点，使杠杆平衡，则有m1·AO=m2·BO，或AO∶OB=m2∶m1.此时，支点O处所承受的质量为mO=m1+m2.

2 杠杆原理在平面几何中的应用

2.1 利用杠杆原理解决平面几何中的比例问题

例1如图在△ABC中，已知点P、Q在边BC上，点G在边AC上，满足BP∶PQ∶QC=3∶2∶1，CG∶GA=2∶3，求BE∶EF∶FG.解设BE,EF,FG的长分别为a,b,c.把线段AC看成杠杆，以G为支点，设mA=2.

由已知条件CG∶GA=2∶3，得mC=3；再把线段BC看成杠杆，以P为支点,由CP∶PB=1∶1，又mC=3，则mB=3；以BG为杠杆，E为支点，由上述结果可得：BE∶EG=a∶(b+c)，mB=3,mG=mA+mC=5，

①

②

联立①②解得：a:b:c=35:15:6，即BE∶EF∶FG=35∶15∶6.

故可设mE=λ，由杠杆原理得mC=1-λ，mB=3λ.

①

②

因为D是BC中点，由杠杆原理知

mB=m，mD=2m.

设mA=n，以AB为杠杆，F为支点得：

AF·n=BF·m，

以AD为杠杆，E为支点，得

AE·n=DE·2m，

2.2 利用杠杆原理解决平面几何中的面积问题

说明本题可作以下的推广

显然，推广(1)是推广(2)的特例，下面我们只需解决推广(2).

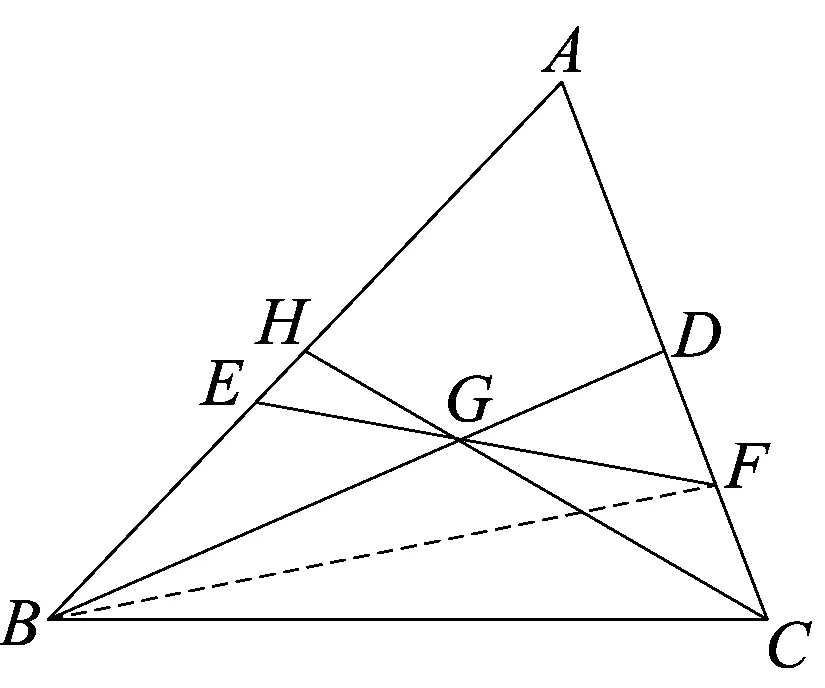
如图，设mC=1，以AC为杠杆，D为支点，

说明此例还可推广到任意比的情形，题设条件同例题.

2.3 利用杠杆原理解决平面几何中的不等关系

①

②

③

把上述①②③三式相加可得：

2.4 利用杠杆原理证明平面几何中重要定理

例9 (梅涅劳斯Menelauss定理)设直线l

情况(2)同理可证.

注：利用同样的方法也可以证明Ceva定理.

2017-03-28)