基于模糊聚类的谷氨酸发酵过程故障诊断研究

张 进， 王贵成,2， 汪 滢

(1.沈阳化工大学院 信息工程学院， 辽宁 沈阳 110142; 2.上海应用技术大学 电气与电子工程学院， 上海 201418)

基于模糊聚类的谷氨酸发酵过程故障诊断研究

张 进1， 王贵成1,2， 汪 滢1

(1.沈阳化工大学院 信息工程学院， 辽宁 沈阳 110142; 2.上海应用技术大学 电气与电子工程学院， 上海 201418)

结合谷氨酸发酵过程，给出模糊聚类故障诊断的方法和步骤，在获取与掌握先验知识后，找到故障数据的聚类中心，运用对比方法预判故障发生的先兆，达到故障诊断的目标.以谷氨酸发酵过程生产故障为例，仿真结果表明模糊聚类的中心值随故障类别不同而不同，初步实现利用模糊聚类方法对样本数据的多级故障诊断，诊断结果与实际情况相符.

模糊聚类； 发酵过程； 故障诊断； 模式识别

随着科学技术水平的发展，谷氨酸发酵工业正逐渐向大型化和自动化的方向发展，过程运行状态的监测成为关键.在实际生产中，研究人员考虑从工艺采集数据中了解系统运行的确切状态，最好在故障前期能及时发现，并采取相应措施，避免故障的发生.国内外许多资料表明，开展生产过程的监控与故障诊断会带来显著的经济效应.现有故障诊断存在知识库庞大、解决问题能力局限、自动获取知识能力差等[1]问题.近年来，随着数据库知识发现技术的兴起，对聚类的研究被众多领域所关注，聚类分析技术己被广泛应用于科学数据探测、信息管理、医学诊断、生物技术、水质分析、金融管理以及过程控制、模式识别和系统辨识等领域，具有广阔的应用前景.聚类分析同时又是一个具有挑战性的领域，由于大型数据库十分复杂，聚类算法必然要面对由此产生的计算需求，它的一些潜在应用成为聚类分析研究的重点[2].因此，对于聚类分析特别是模糊聚类分析进行研究具有非常重要的意义.本文结合谷氨酸发酵过程的生产实际，分析模糊聚类方法，实现生产过程一类故障状态的诊断.

1 模糊聚类算法的应用

谷氨酸发酵过程是复杂的非线性系统，其反应过程极其复杂[3].鉴于发酵工业存在问题的严峻性，迫切需要建立一种能与发酵过程特征相吻合、完整而又具有相同特性、实际操作简单的过程故障诊断技术.一般情况下，利用现有数据库和规则的模式多数已被故障诊断专家系统采用，而专家系统亟待解决的首要问题是数据库规则的有效获取.由于模糊聚类算法的应用，可以在数据自身所展现的信息中攫取知识并抽出所需信息，故而为解决专家系统获取知识困难的问题和处理含糊不清的知识提供了新的途径.

模糊聚类算法是一种数据驱动的软计算方法，它可以分析特征变量相对于控制决策的重要程度，最终整理出简明的决策规范.基于这些特点，将其应用于生产过程故障诊断，可经济有效地解决谷氨酸发酵过程中一些难以解决的问题.

一个基于模糊聚类的故障诊断过程可分成4个步骤：第1步要进行信息的采集.信息采集的过程就是对处理对象的调查与了解，进而从里面获取需要的关键数据和重要资料.第2步要进行信息的预先处理.信息预处理的过程相当于除去外界干扰和差异，将原本的对象变成一种可以被随时提取的计算机特征形式.第3步要进行特征的提取.特征提取作用是为了把已经获取的材料数据进一步的归纳整理从而去粗存精并找到本质特征.第4步需要分类决策，运用某一类的判别算法和判别规则对现有信息进一步分类和辨识，进而获得识别的结果，在这一过程中，需要考虑的是分类有效性.

文献[4]中主要采用的是K-均值聚类算法，它是将数据点与原型之间的某种距离当作优化目标函数，通过函数求极值的算法取得迭代运算的一个调整规则.该算法具有简单快速、适于处理大数据集等优点，在没有任何先验知识的情况下，K-均值聚类状态诊断模型能够很好地区分故障数据和正常数据，但它不能同时区分多种故障，并且该算法对初始值的选取依赖性极大,对于大的数据量，算法开销很大.所以本文应用的是模糊C均值聚类算法，同时解决了以上问题.

2 模糊C均值聚类算法的实现步骤

模糊C均值算法原理具有很强的代表性，很多其他的算法是在其基础上添加约束条件或者操作步骤发展而来的，是基于对目标函数的优化基础上的一种数据聚类方法[5].

模糊C均值算法(FCM)先初始化聚类中心(或者隶属度矩阵)，然后进行迭代直至满足设定的终止条件.具体步骤如下：

步骤1，初始化.令模糊加权指数m=2，聚类类别数C(2≤C≤n)、数据样本点数量n、迭代停止阂值ε、最初的聚类中心值P(0)，及迭代的次数l=0[6]；

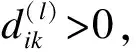
(1)

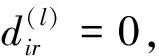
步骤3，聚类中心值的更新.

(2)

步骤4，若‖P(l+1)-P(l)‖<ε，则算法停止，否则转到步骤(2).

式中：m>1是模糊系数；U=uik是一个c×n的模糊划分矩阵，uik是第k个样本xk属于第i类的隶属度值；dik=‖xk-vi‖表示从样本点xk到中心vi的距离.关于隶属度的迭代公式是一个从点到集合的映射，在实际计算中通常采用如下的隶属度更新公式：

(3)

3 基于模糊聚类算法的故障诊断研究

模糊聚类可以用来间接地识别因果关系，基本思想是以现在的故障征兆群与以前的各次诊断的征兆情况对比[7]，找出本次的故障与以前已确定的故障中哪次最为类似，就可认为本次故障起因与以前类似故障的起因相像，因此可参考历史经验来认定当前最可能的故障起因，从而取得较满意的结论[8].

运用模糊聚类算法的实现故障诊断，大体上可分为3大步骤：

步骤1，提取对象的特征.即把与对象x相关的各个特征从中提取出来，同时把x在诸特征上的详细数据测出来；

步骤2，隶属函数的建立.即先明确算法，再把隶属于它的矩阵U初始化，Ai的隶属度uAi(x)是x，并且依赖于x1,x2,…,xn.

步骤3，识别对象的判定.根据一定的规则识别判定对象x，找到其对应的归属类型及其分类的行之有效性[9].

操作流程：首先选取特征变量建立样本参数空间，对样本的各特征值进行标准化处理，确定聚类数C，模糊加权系数m，按约束条件初始化隶属度矩阵设定一个任意小的迭代误差阈值，然后不断地计算更新模糊划分矩阵和聚类中心，直到系统达到稳定状态，迭代停止，输出结果.

4 模糊聚类应用于谷氨酸发酵过程故障诊断研究

实验所用的数据全部来自于某味精厂生产车间的记录数据，此次研究的目标为谷氨酸正常发酵与异常发酵的发酵液的质量浓度.选取4个批次谷氨酸发酵过程的记录数据，其中有一个批次的谷氨酸发酵最终质量浓度超过10 g/L，将其认为是正常发酵.此外，还有3个批次的谷氨酸发酵最终质量浓度没有达到10 g/L，其最终结果的质量浓度最大值仅有5.3 g/L，将其认为是非正常发酵.3种非正常发酵故障情况分别是搅拌机故障引起的溶氧故障，氨水添加故障和染菌故障.表1和表2是原始正常数据和故障数据.图1是3种故障和正常情况下的分类结果.

表1 发酵过程30组正常数据

表2 15组故障数据

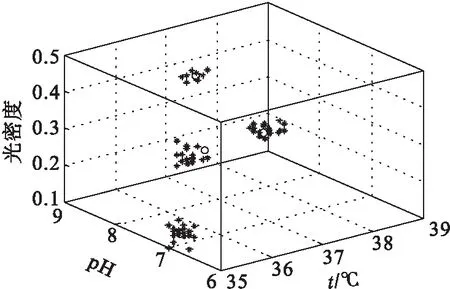
图1 3种故障和正常情况下的分类结果

经模糊聚类处理，最后得到的群中心值为：

37.4 8.8 0.4 16.1 4 000

37.3 7.4 0.3 14.3 3 400

35.3 7.0 0.1 15.4 2 800

37.3 8.6 0.2 12.1 3 400

迭代过程的递归循环次数为19，成本函数值为2.38，数据被准确分为4类，得到的聚类中心被认为是某种状态的标准特征点.截取其中30组数据进行分析.隶属度矩阵见表3.从表3可以看出：每组数据对各个聚类中心的隶属度不同，以此形成了不同的故障群和正常状况群划分.每一组数据隶属于某个状态类的大小不同，可以反映出该数据更接近于那个状态.通过这个隶属度矩阵也可以看出故障的严重程度.数据点对于故障中心的隶属度越大，说明发生故障的可能性就越大.比如第18组数据对聚类中心点4的隶属度最高，为0.95，而对其他中心点的隶属度都很小，说明该点处发生染菌故障可能性很大，几乎可以确定.与之相对，第30组数据则对每一个中心点的隶属度都在0.6以下，其中对染菌的中心点隶属度又为最高是0.58，接近0.6.据此可以推断该数据点处的状态有可能是染菌初期，因为它具有一些染菌状态的相似信息.实验分析得出前，在表3中出现的3种故障有标准故障状态集合的情况下，这种分类的方法可以快速的对数据进行分类.

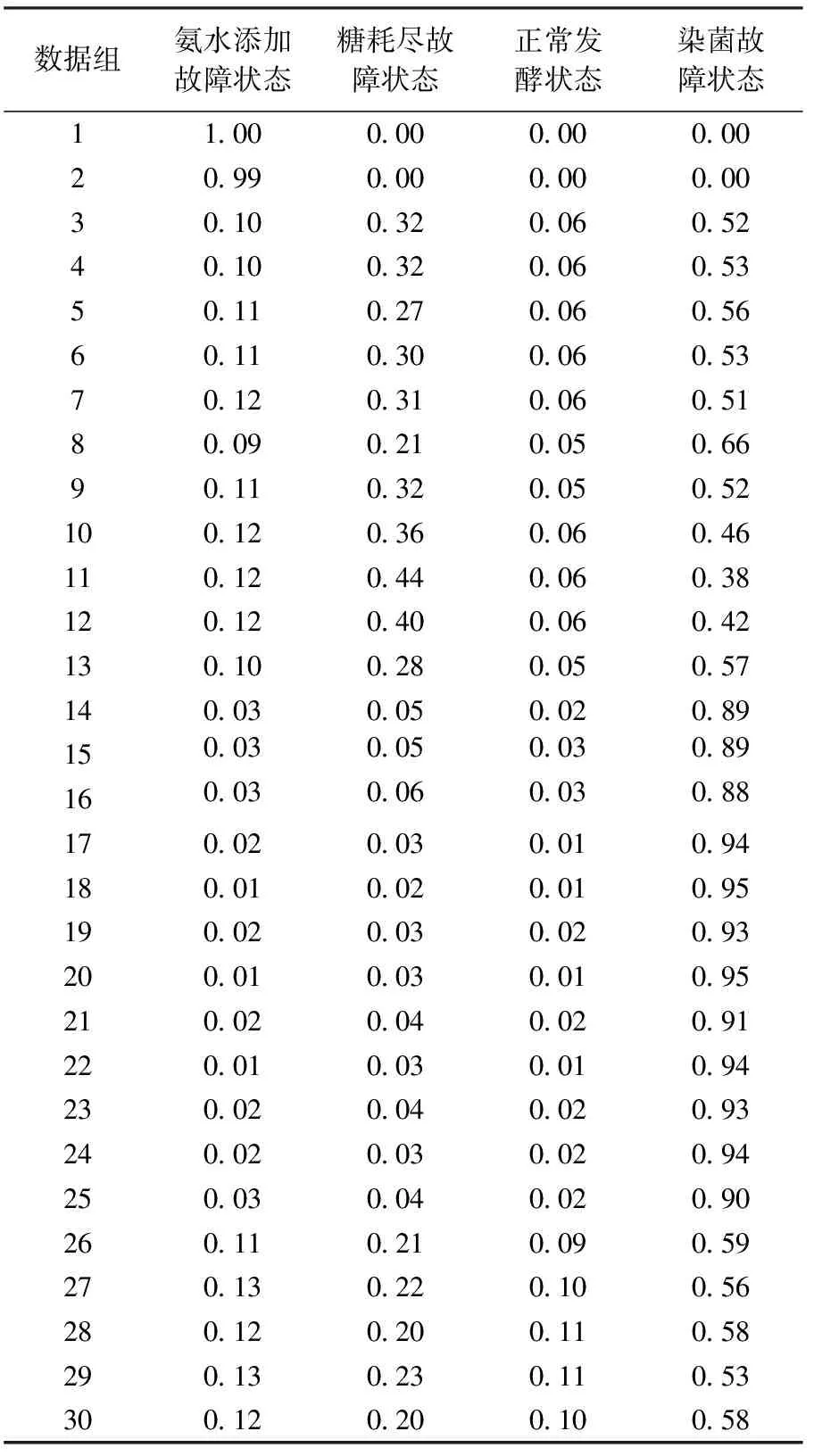
表3 多故障数据实验结果的隶属度矩阵

下面通过染菌故障的诊断问题来分析对比较大的状态数据集合分多个聚类中心聚类的问题.从生产过程中的染菌故障数据中随机选取100组数据，并加入50组正常数据同时输入故障诊断模型.由于输入数据较多，初始还不知道最佳分类数是多少，暂定分类数为2，得到结果的聚类图如图2所示，从隶属度矩阵中选取40组数据进行分析，如表4所示.

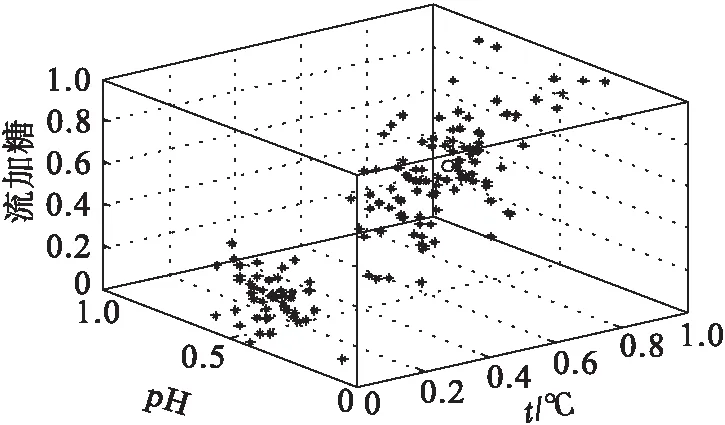
图2 染菌故障分析结果

表4 模糊聚类数为2时染菌样本数据隶属度矩阵

聚类之后得到的聚类中心为

迭代过程的递归循环次数为26，成本函数值为21.6.从聚类结果可以看到隶属度矩阵中的值很清楚地反映出数据点和聚类中心的关系：隶属度越大，说明数据点和这个数据类相似度越高，对应该状态发生的可能性越大，反之则越小.

从表4看到大部分数据点能以较大的隶属度归于某一类中，但是有些数据点特征不明显，它对于两类的隶属度值很接近，例如表4中第19组数据，对于故障类的隶属度为0.47，对于正常类的隶属度为0.53，这个结果说明它属于两类中间，不具有某种状态的明显特征，因此尝试将聚类数目改为3，再来看一次聚类结果，如图3所示.从隶属度矩阵中选取30组数据来分析，如表5所示.

图3 聚类中心数为3时的染菌故障样本聚类结果

表5 聚类中心数为3时的染菌样本数据隶属度

聚类之后得到的聚类中心为

迭代过程的递归循环次数为78，成本函数值为45.7.从聚类结果可以看出：这次聚类的数据点给出更为合理的聚类.数据隶属于某一类的隶属度相对于另外的两组有了比较大的区别，如第30组数据相对正常状态的隶属度为0.80，而相对于另外两组的隶属度分别为0.03，0.16，0.80相对0.03和0.16要大很多，说明该数据点和这个聚类的特征相似度较高，发生的可能性大.反之发生的可能越小.基于此，可以提出诊断的处理模型，在生产中将故障源从数据群中提取出来，然后将输入进来的待测数据和故障源中的数据进行分类，得到结果距离哪个聚类中心最近，发生哪种故障的可能性也越大.这里分2个故障类就代表了2种情况，染菌前期和后期，染菌前期情况并不明显，数据反映不剧烈，因此既不完全属于正常的类，也不完全属于染菌后期的标准故障类.

5 结 论

根据大量研究指出，文中所给出的模糊聚类研究方法对总体分析谷氨酸的发酵过程中出现的故障有明显的效果，而且还减轻了诊断的工作任务，减少了诊断时间.对于高维特征空间的故障数据信息和正常数据信息能够很好地区分，对于多种故障信息和正常数据信息也有良好的聚类效果.对于染菌故障中大批量的数据处理，可以通过计算得到多个聚类中心，提取出染菌故障不同阶段的特征信息；可以不依赖大量的先验知识，只通过将生产过程采集来的数据同故障源数据对比分析即可得出结论.模糊聚类分析方法用于故障诊断尚有许多难题需要解决，例如用来分析的聚类样板比较少，就会出现分析结果的精确率下降等一系列问题；因此要与生产实际相结合，尽可能地在生产现场做大量故障记录，丰富各类故障样本，以提高判别的准确率.

[1] FRANK P M.New Developments Using AI in Fault Diagnosis[J].Engineering Applications of Artificial Intelligence,1997,10(1):3-14.

[2] 阳琳赟，王文渊.聚类融合方法综述[J].计算机应用研究,2005,22(12)：8-10.

[3] 高敏杰，丁健，张许，等.基于支持向量机和模糊推理的毕赤酵母发酵过程故障诊断[J].食品与生物技术学报，2014，33(11)：1182-1190.

[4] 廖松有.模糊C均值与K均值聚类算法及其并行化[D].太原：太原科技大学电子信息系，2013:43-55.

[5] 陈琳,何嘉.基于模糊聚类的粒子群优化算法[J].西南民族大学学报(自然科学版),2007,33(4):39-42.

[6] 刘曼兰.永磁直流电机故障在线监测与智能诊断的研究[D].哈尔滨:哈尔滨工业大学电机与电器系，2007:92-93.

[7] 王清,潘宏侠,周传刚.机械故障诊断技术现状及趋势[J].机械管理开发,2005,20(6):49-51.

[8] 曾辉.模糊逻辑在机械故障诊断中的应用[D].燕山：燕山大学逻辑学系，2007：26-27.

[9] 陈凌.基于模糊聚类算法的图像分割方法研究[D].江西:江西理工大学计算机应用技术系,2012:28-29.

Fault Diagnosis for Glutamic Acid Fermentation Process Based on Fuzzy Clustering

ZHANG Jin1, WANG Gui-cheng1，2, WANG Ying1

(1.Shenyang University of Chemical Technology, Shenyang 110142, China; 2.Shanghai Institute of Technology, Shanghai 201418, China)

Combined with glutamic acid fermentation process, the method and step of fault diagnosis of fuzzy clustering are given, especially after obtaining and mastering the prior knowledge, to find the clustering center of fault data, and using the contrast method to predict the fault omen and realize the goal of fault diagnosis.For glutamic acid fermentation process, process,production fault as an example,the simulation results show that the central value of fuzzy clustering is different with fault category.The multi-level fault diagnosis is realized by fuzzy clustering for sample data,and the diagnosis result is consistent with the actual situation.

fuzzy clustering; fermentation process; fault diagnosis; pattern recognition

2015-03-20

张进(1992-)，女，辽宁沈阳人，硕士研究生在读，主要从事智能控制算法的研究.

王贵成(1972-)，男，辽宁抚顺人，副教授，博士，主要从事复杂过程建模与控制研究.

2095-2198(2017)02-0182-06

10.3969/j.issn.2095-2198.2017.02.018

TP182

： A