基于张紧装置的高速电梯提升系统振动控制

包继虎， 张 鹏， 朱昌明， 朱 明， 金丽琼， 谢鸿玺

(1.合肥通用机械研究院，合肥 230031；2. 上海交通大学 机械与动力工程学院，上海 200240)

基于张紧装置的高速电梯提升系统振动控制

包继虎1， 张 鹏2， 朱昌明2， 朱 明2， 金丽琼1， 谢鸿玺1

(1.合肥通用机械研究院，合肥 230031；2. 上海交通大学 机械与动力工程学院，上海 200240)

考虑提升系统横向和纵向的耦合作用。应用广义Hamliton原理建立了带有张紧补偿钢丝绳的高速电梯提升系统振动控制方程，并以高速电梯提升系统为例对模型进行了数值仿真分析。结果表明：张紧装置的增加能有效抑制提升系统振动，一方面从理论上分析和解释了具有张紧装置的补偿钢丝绳可以大大减小提升系统振动的原因，另一方面说明选择张紧装置抑制提升系统振动的合理性，研究工作为下一步高速电梯提升系统振动控制器的实际应用提供了具有建设性的方法及其思路。

高速电梯；提升系统；钢丝绳；张紧装置；振动控制

由于设计、制造以及安装等方面的缺陷，电梯在运行过程中，不可避免地会产生各种各样的振动现象，其中很大一部分与电梯的提升系统有关[1]。另外，随着电梯运行速度和提升高度的增加，提升系统在运行时对外界干扰更加敏感，异常的振动更容易发生，其后果会加剧钢丝绳的磨损和疲劳，缩短钢丝绳的使用寿命，同时，轿厢内可能产生噪声，其结果会使轿厢内的乘客感到不适，影响电梯的使用寿命以及乘坐舒适性[2-5]。

为此，国内外许多学者针对电梯提升系统的振动控制提出了许多新的理论和方法[6]，其采取的控制措施从振源的引入上来区分主要有两类：一是采用可行的控制策略以减小或抑制导轨、导靴等结构件引入的振动对轿厢体的影响[7]，二是采用可行的控制策略以减小或抑制曳引绳、曳引机组等结构件引入的振动对轿厢体的影响[8]，部分学者提出将控制器置于轿厢顶部上方的钢丝绳上[9]，理论上是可行的，但实施于实际电梯提升系统中，有一定的难度，原因主要是由于电梯曳引钢丝绳通常由五根到八根或更多根组成，将主动控制器同时布置于多根钢丝绳上，对控制器灵敏度要求较高，而且电梯在运行时，曳引钢丝绳的长度是变化的，因此，很难保证其控制的实时性。另外，目前电梯多采用复绕式，这也导致主动控制器很难布置于钢丝绳上。基于以上分析，本文提出了通过张紧钢丝绳与曳引钢丝绳的耦合关系进而达到控制曳引钢丝绳振动的目的，以期获得理想的控制策略，为电梯提升系统的振动控制提供有益的理论依据。

1 基于张紧结构的提升系统控制模型

此模型主要由曳引钢丝绳和张紧钢丝绳(采用与曳引钢丝绳同类型钢丝绳进行张紧)构成，曳引绳和张紧绳的线密度为ρ，横截面积分别为S，弹性模量为E。选取曳引绳与曳引轮相切点为坐标圆点，X轴垂直向下的方向为正向，Y轴水平向右的方向为正向，系统简化模型，如图1所示。在运动过程中记曳引钢丝绳绳长为l(t)，曳引轮与张紧轮轮心之间的距离为L，张紧轮通过刚度为kt的弹簧和阻尼为ct的阻尼器固定于底坑，以模拟张紧装置。轿厢体与导轨之间采用刚度为k的弹簧和阻尼为c的阻尼器连接，以模拟导靴装置。在提升系统中的纵向和横向振动位移分别为u(x,t)和v(x,t)，υ(t)为电梯提升系统的轴向运行速度，a(t)为电梯提升系统的纵向运行加速度。同时，本章的建模和求解基于以下三个假设：

(1)钢丝绳中由于纵向和横向振动引起的弹性变形远小于钢丝绳的长度；

(2)钢丝绳具有连续和均匀性，其线密度ρ、横截面积S、弹性模量E在运动过程中保持不变，同时忽略钢丝绳的阻尼影响；

(3)不考虑摩擦力的影响，同时忽略井道内气流的影响。

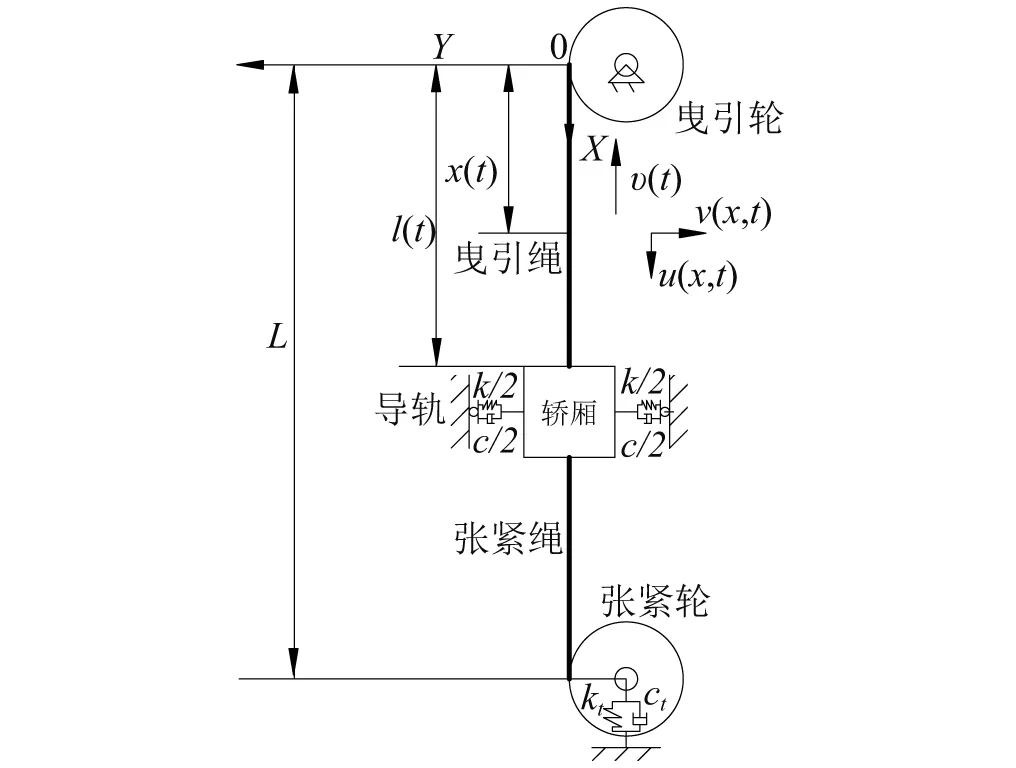
图1 电梯提升系统示意图Fig.1 Schematic of the elevator hoisting system

由图1可知，提升系统在整个运行过程中的动能可表示如下

(1)

由于钢丝绳和轿厢自身重量以及预张紧力F的作用，曳引钢丝绳和张紧钢丝绳中x处在t时刻的张紧力可表示为

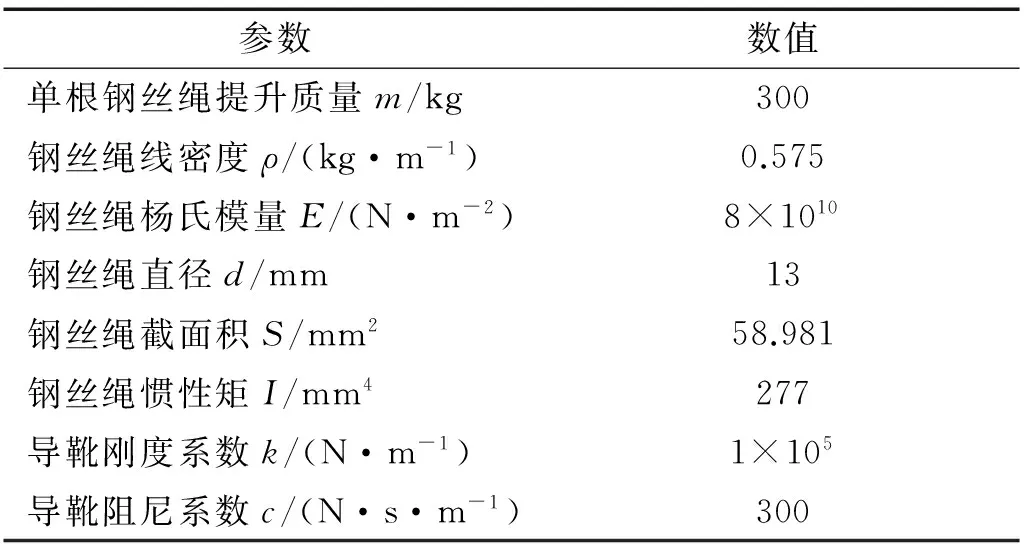
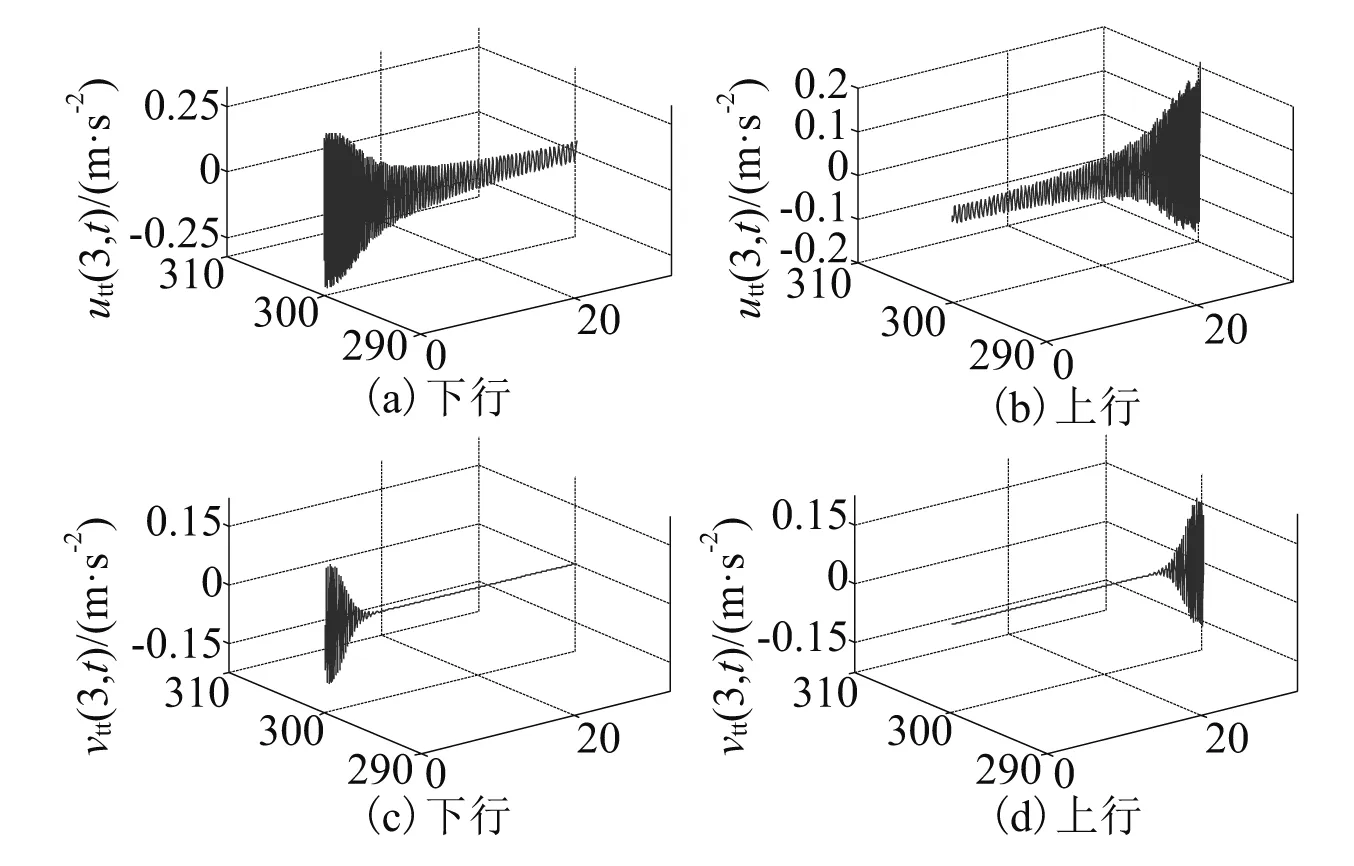
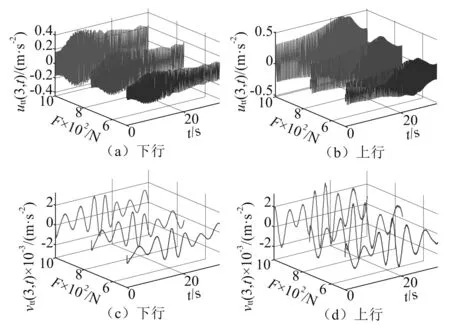
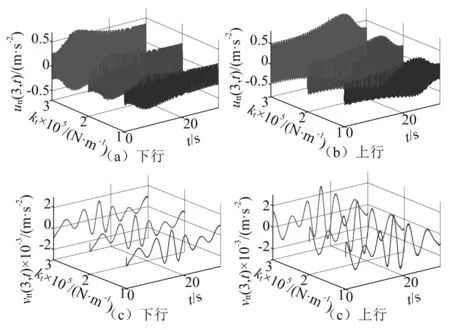
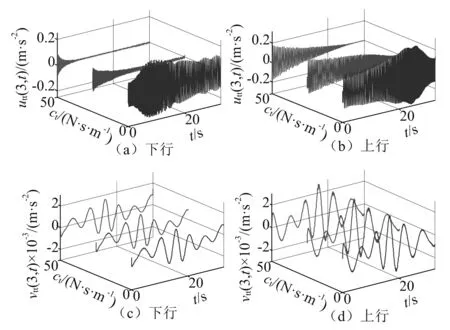
T1(x,t)=[m+ρ(L-x)]g+F,0

(2)

T2(x,t)=ρ(L-x)g+F,l+(t)

(3)

提升系统的弹性势能可表示为：

Ee=0.5ktu2(L,t)+0.5kv2(l,t)+

(4)

式中：ES为钢丝绳的抗拉刚度；EI为钢丝绳的抗弯刚度。提升系统的重力势能可表示为

(5)

系统中各类阻尼力所作的虚功可表示为

(6)

将上述所描述的动能、弹性势能、重力势能和虚功代入广义Hamliton原理，即

(7)

结合Leibnitz定律和分部积分方法，即：

(8)

(9)

同时，在上述运算过程中应用时间边界条件和几何边界条件：

(10)

(11)

将式(1)、式(4)～式(6)代入式(7)得到提升系统的振动控制方程和相应的导出边界条件。

(12)

(13)

(14)

m(vtt+2υvxt+avx+υ2vxx)+

c(vt+υvx)+kv+(T1vx)l--(T2vx)l++

(15)

式(12)和式(13)即为电梯提升系统振动控制方程，式(14)和式(15)是对应于提升系统振动控制方程的导出边界条件。

2 受控模型数值求解

假设存在正交化本征函数φu,i(x,t)和φv,i(x,t)，且：φu,i(x,t)=φu,i(ξ)和φv,i(x,t)=φv,i(ξ)，其中ξ=x/L。纵向振动和横向振动解的正交化本征函数可分别选择[10-12]

(16)

(17)

假设式(12)和式(13)的解可分别表示为无限自由度的分布参量函数u(x,t)和v(x,t)

(18)

(19)

式中：qu,i(t)和qv,i(t)是仅与时间有关的广义坐标；i=1,2,…,n，n为模数。在对式(14)和式(15)进行求解之前，首先需要将其近似解按方程中的偏导数进行展开。由式(18)和式(19)可知

(20a)

(20b)

(20c)

(20d)

(20e)

(21a)

(21b)

(21c)

(21d)

(21e)

(21f)

(21g)

将式(20)和式(21)代入式(12)，两边同时乘以φu,j(x/L)，并将其分别在[0,l-]和[l+,L]范围内进行积分，然后将积分后的两式相加，结合导出边界条件式(14)，应用Galerkin加权余量法，即可得到离散化的提升系统纵向振动控制方程。将式(20)和式(21)代入式(13)，两边同时乘以φv,j(x/L)，并将其分别在[0,l-]和[l+,L]范围内进行积分，然后将积分后的两式相加，结合导出边界条件式(15)，应用Galerkin加权余量法，即可得到离散化的提升系统横向振动控制方程。将上述两个方程整理得：

(22)

式中：Qu=[qu,1(t),qu,2(t),…,qu,n(t)]T和Qv=[qv,1(t),qv,2(t),…,qv,n(t)]T分别为纵向和横向振动的广义坐标向量，Mu，Mv，Cu，Cv，Ku，Kv和Fu，Fv分别为与广义坐标向量Qu和Qv对应的质量、阻尼、刚度和广义力矩阵，Pu和Pv为广义坐标耦合项。式(23)中各元素表达式见附录。考虑上述广义坐标的初始条件，对常微分方程式(22)进行求解，可得到广义坐标向量Qu和Qv，将其分别代回式(18)和式(19)即可得到提升系统中钢丝绳的纵向和横向振动位移的实时值。

3 应用分析

下面将结合应用实例对加装张紧器的电梯提升系统的振动特性进行分析，以验证张紧器对提升系统振动的抑制效果，同时，为了掌握张紧器的刚度和阻尼等参数对于提升系统振动抑制效果的影响，允许其刚度和阻尼系数在一定范围内取值。

3.1 参数

高速电梯提升系统的详细参数如表1所示。提升系统的运行状态参数分别为：顶层高度l0=8 m、最大提升高度lmax=131 m、最大速度υmax=5 m/s、最大加速度amax=1 m/s2、最大加加速度jmax=1 m/s3，各阶段运行时间分别为：tj=1.5 s、ta=3.5 s、tυ=20 s，应用文献[1]的方法可得到提升系统理想运行状态曲线，如图2所示。

表1 电梯提升系统参数

图2 电梯运行曲线Fig.2 Movement profile of the elevator

提升系统中预加张紧力F=500～1 000 N。此处张紧力的施加需要考虑钢丝绳的安全系数，由于所选钢丝绳破断张力为74.3 kN，由此，由GB 7588—2003可以确定提升钢丝绳安全系数：St=74.3×103/(m×9.8+ρ×l(t)×9.8+F)>12。因此，所选预加张紧力是合理的。张紧器的刚度系数kt=1～3×105N/m，张紧器的阻尼系数ct=0～50 N·s/m。

3.2 计算结果及分析

将表1描述的参数代入式(22)即可得到增加张紧钢丝绳后提升系统在不同情况下的振动加速度响应曲线。图4～图6分别给出了在不同参数情况下，电梯运行过程中轿厢上方3 m处提升系统的振动加速度响应曲线。为了比较增加张紧钢丝绳后对系统振动的抑制效果，图3给出了未增加张紧钢丝绳的轿厢上方3 m处钢丝绳的振动加速度响应曲线。通过比较发现，在增加张紧装置后，电梯提升系统横向振动加速度响应得到了很好的抑制，但纵向振动加速度响应抑制效果不如横向振动明显，其主要原因是由于引入的预加张紧力作用，导致钢丝绳纵向受力情况发生变化引起的，从图4还可知，随着张紧力的增加，纵向振动加速度还有增大的趋势。因此，通过增加预加张紧力能较好的抑制提升钢丝绳的横向振动，但并不能很好地抑制纵向振动，较大的预加张紧力还可能恶化纵向振动。从图5中可知，随着张紧装置刚度系数的增加，纵向振动加速度响应有增大的趋势。但从图6可知，当在系统中考虑张紧器阻尼特性时，纵向振动加速度响应能得到较好的抑制，而且随着阻尼值的增加，纵向振动抑制的效果非常明显。

图3 钢丝绳的振动加速度响应Fig.3 The vibration acceleration of the rope

图4 不同张力时曳引钢丝绳的振动加速度Fig.4 The vibration acceleration of the rope with different tension

图5 不同刚度时曳引钢丝绳的振动加速度Fig.5 The vibration acceleration of the rope with different stiffness

图6 不同阻尼时曳引钢丝绳的振动加速度Fig.6 The vibration acceleration of the rope with different damping

因此，为了达到有效抑制系统振动的目的，张紧装置应该选择小刚度大阻尼的系统。显然，要实现小刚度大阻尼的结构，在实际应用中是很容易实现的。通过合理的结构设计，还可以使张紧器中的阻尼值在某个较大的范围内进行调整，以满足高速电梯在不同环境下的要求。

4 结 论

本文从理论上对高速电梯提升系统的振动控制进行了研究，提出了基于系统张紧装置的振动抑制方式，并接合算例对控制方法的效果进行了仿真分析，结果表明，张紧装置能有效抑制系统的振动，由此证明提升系统中增加张紧装置抑制振动是合理的。此研究工作为下一步电梯提升系统振动控制器装置的实际应用打

下了理论基础，并提供了建设性的思路和方法。

[1] 包继虎, 张鹏, 朱昌明. 变长度提升系统钢丝绳纵向振动特性[J]. 振动与冲击, 2013, 32(15): 173-177. BAO Jihu, ZHANG Peng, ZHU Changming. Longitudinal vibration of rope hoisting system with time-varying length[J]. Journal of Vibration and Shock, 2013, 32(15): 173-177.

[2] MEI D, DU X, CHEN Z. Optimization of dynamic parameters for a traction-type passenger elevator using a dynamic byte coding genetic algorithm[J]. Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2009, 223: 595-605.

[3] BAO J H, ZHANG P, ZHU C M. Transverse vibration of flexible hoisting rope with time-varying length[J]. Journal of Mechanical Science and Technology,2014,28(2)：457-466.

[4] REN H. Accurate simulation of the dynamics of elevator systems[D]. Baltimore,MD:University of Maryland, Baltimore, 2011.

[5] ANDREW P, KACZMARCZYK S. Rope dynamics[J]. Elevator World, 2011, 38: 45-56.

[6] LEE Y M, KANG J K, SUL S K. Acceleration feedback control strategy for improving riding quality of elevator system[J]. Conference Record of the 1999 IEEE, 1999, 2: 1375-1379.

[7] KANG J K, SUL S K. Vertical-vibration control of elevator using estimated car acceleration feedback compensation[J]. Industrial Electronics, IEEE Transactions, 2000, 47(1): 91-99.

[8] ARAKAWA A, MIYATA K. A variable-structure control method for the suppression of elevator-cage vibration[J]. IECON 02, 2002, 3: 1830-1835.

[9] ZHU W D, NI J, HUANG J. Active control of translating media with arbitrarily varying length[J]. Journal of Vibration and Acoustics, 2001, 123: 347-358.

[10] 张鹏, 朱昌明, 张梁娟. 变长度柔性提升系统纵向-横向受迫耦合振动分析[J]. 工程力学, 2008, 25(12): 202-207. ZHANG Peng, ZHU Changming, ZHANG Liangjuan. Analysis of forced coupled longitudinal-transverse vibration of flexible hoisting systems with varying length[J]. Engineering Mechanics, 2008, 25(12):202-207.

[11] ZHANG P, ZHU C M, BAO J H, et al. Horizontal vibration of car in the flexible suspension system of elevator[C]∥The 3th edition of Symposium on the Mechanics of Slender Structures. San Sebastian ,Spain：MoSS2010，2010.

[12] ZHANG P, BAO J H, ZHU C M. Dynamic analysis of hoisting viscous damping string with time-varying length[J]. Journal of Physics: Conference Series, 2013, 488(1)：1-9.

附录1

式(23)中各元素表达式为

Vibration control of high-speed elevator hoisting systems based on tensioning devices

BAO Jihu1，ZHANG Peng2，ZHU Changming2，ZHU Ming2，JIN Liqiong1，XIE Hongxi1

(1. Hefei General Machinery Research Institute, Hefei 230031, China;2. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The governing equations of the high-speed elevator hoisting system with a tensioning device were developed employing the generalized Hamlton’s principle considering the horizontal and vertical motion coupling effect. The motions of the high-speed elevator hoisting system were illustrated to evaluate the proposed mathematical model and solution method. The simulation results show that the tensioning device can effectively control the vibration of the hoisting system. The reasons that the vibration of the hoisting system can be greatly reduced by the compensating rope with tensioning device were analysed and explained. It is also shown that the choice of the tensioning device is reasonable to suppress the vibration of hoisting system. The results provide a constructive way and idea for the practical application of vibration controllers.

high-speed elevator; hoisting system; rope; tensioning device; vibration control

国家自然科学基金青年基金项目(51205249)

2016-01-12 修改稿收到日期：2016-05-25

包继虎 男， 博士， 助理研究员， 1977年生

张鹏 男， 博士， 高级工程师， 1978年生

TH211.06

A

10.13465/j.cnki.jvs.2017.14.035