反应加速度法和反应位移法精度随结构埋深变化的研究

董正方， 蔡宝占， 姚毅超， 李凤丽， 朱红云

(1. 河南大学 材料与结构研究所， 河南 开封 475004； 2. 中铁二院华东勘察设计有限责任公司 杭州 310004)

反应加速度法和反应位移法精度随结构埋深变化的研究

董正方1， 蔡宝占1， 姚毅超2， 李凤丽1， 朱红云1

(1. 河南大学 材料与结构研究所， 河南 开封 475004； 2. 中铁二院华东勘察设计有限责任公司 杭州 310004)

从理论方程上，看不出反应加速度法和反应位移法的精度会随地下结构埋深而变化，因此为确定其精度，设定不同场地条件下、不同埋深的城市轨道交通箱型地下结构为基准模型。使用反应加速度法、反应位移法、修正的反应位移法和时间历程法计算基准模型的结构内力，评价前三种方法随埋深变化的精度。结果表明：前三种方法的精度会受到场地类型、土层厚度和结构埋深的影响；若以时间历程法为基准，反应位移法的精度要低于反应加速度法和修正的反应位移法；反应加速度法和修正反应位移法的精度受埋深影响较小，反应位移法在埋深较小时精度尚可。

反应加速度法；反应位移法；地下结构；抗震设计

我国正在兴建城市轨道交通结构，其中大部分位于抗震设防区，因此其抗震设计日益重要。城市轨道交通结构包括大量的地下车站和区间隧道，而对这些结构的抗震设计一般分为横向抗震和纵向抗震，横向抗震一般采用拟静力方法，目前常用的有反应加速度法和反应位移[1]，这类方法都有不同程度地简化和假定，因此都有其适用范围和精度[2]；横向抗震的时间历程法一般作为校核其他方法或深入研究使用。

20世纪60年代，日本通过松代群发地震中埋设管道的地震观测研究，逐步提出了反应位移法，将地下结构的横断面模型化为框架式结构，周围施加地基弹簧[3]。20世纪80年代，日本提出把地下结构周围的土体用平面单元来模拟的思路，Tateishi[4]的地层响应法、片山幾夫等[5]的地层反应加速度法，以此为基础发展的一类方法就是反应加速度法。近年来，国内逐渐接受并推广反应位移法和反应加速度法，上海地方标准《地下铁道建筑结构抗震设计规范》(DG/T J08-2064—2009)、国家标准《城市轨道交通结构抗震设计规范》(GB 50909—2014)都引入了上述方法。国内的研究者，例如商金华等[6-7]对上述方法的荷载模式进行了研究，并提出了修正的方法，但都没涉及方法随结构埋深的变化的精度问题；陶连金等[8]给出了不同埋深下的该类方法的精度研究，但土层厚度只有20 m，而实际的城市轨道交通地下结构所处土层的厚度、埋深都不仅限于20 m，因此本文将做进一步的研究。

1 理论推导

为了说明两种方法随结构埋深变化的精度问题，首先从理论上对两种方法进行推导。

1.1 反应加速度法

反应加速度法的模型最初有两种：①立石彰模型，如图1(a)所示，在侧向边界和底部边界上施加土层剪应力，土层剪应力可由一维土层反应得到；②片山模型，如图1(b)所示，把侧向边界竖向约束、水平自由，底部边界约束。实际上这两种模型是等价的，图1(b)的侧向边界的竖向约束力等于图1(a)的土层剪应力，但是图1(a)模型不适宜有限元建模，因此实际较多采用图1(b)模型。

立石彰以子结构的方法对反应加速度法进行了理论推导，基于三个假定：①设地下结构与近场土为子结构，其边界设置在较远处，则地下结构不影响边界反应；②忽略阻尼力；③地下结构的加速度认为等于相同位置的土层加速度。实际上反应加速度方法基本公式的推导完全可以考虑阻尼的作用，对图1(c)考虑土-结构动力相互作用模型，其地震作用下的运动方程如下[9]：

(1)

式中:K、M、C分别为刚度、质量、阻尼矩阵;其下标b为边界；上标T为转置；上标ve为黏弹性边界；u为位移向量，位移向量上的“·”和“··”分别为对时间的一阶和二阶导数；pb,eff为边界上的等效作用力；方程左边第一项为惯性力，第二项为阻尼力项，第三项为恢复力。

(a)立石彰模型 (b)片山模型 (c)土-结构动力相互作用模型图1 反应加速度法模型Fig.1 Model of response acceleration method

依照立石彰的思路，将惯性力和阻尼力移到右边，则地震运动方程可以化为

(2)

(3)

这就是基于图1(b)模型的反应加速度法理论方程，因为阻尼力不方便计算，实际使用时经常省略阻尼力。

1.2 反应位移法

反应位移法也可以从上述运动方程导出，由于是拟静力计算，因此忽略阻尼影响，人工边界采用地基弹簧模拟，如图2(a)所示。将人工边界上的输入地震作用分解为两个等效地震动荷载：自由场地震动引起的对应于人工边界处的应力场；使人工边界上的弹簧阻尼器到达人工边界处的自由场位移所需要的力，即将人工边界的弹簧阻尼器强制拉到人工边界处的自由场位移时所需的力[10]。则运动方程化简为

(4)

(5)

式中:下标b即土与结构交界面，因为边界取在结构周边；pbf为入射波场(自由场)在结构周边产生的作用力；ubf为入射波场(自由场)在结构周边产生的位移。把式(5)代入式(4)，并把惯性力项移到方程右边，可得：

(6)

这就是反应位移法的理论方程，其中方程右边第一项表示的自由场土层相对位移引起的等效荷载；第二项是土层对地下结构的作用力；第三项是惯性力；如果地震动垂直入射，则位移只有水平位移分量，土层对结构作用力只有剪切分量，即土与结构交界面土层剪应力，由自由场一维地震反应分析得到。

为了直接反映土-结构相互作用，同时避免计算地基弹簧系数的复杂性，刘晶波等采用如图2(b)所示的土-结构有限元模型。常用的反应位移法中包括三部分荷载：土层相对位移、结构周围土层剪力、惯性力。对于第一部分作用，反应位移法在地基弹簧端部施加相对变形，此时在结构上产生的反力即为土层相对变形引起的等效荷载，由于地基弹簧模拟的是周围土层约束作用，因此为了直接计算图2(b)中位移等效荷载，可在挖去结构的土体模型中沿着孔洞周围施加相对位移，此时孔洞周边结点(要施加约束)反力即为等效荷载。结构周围剪力及结构惯性力与反应位移法完全相同。

(a)常用模型 (b)修正模型图2 反应位移法计算示意图Fig.2 Model of response displacement method

由上述两种方法的理论推导，看不出方法的精度随结构埋深变化，下面通过典型算例进行精度的研究。

2 典型算例

2.1 算例参数

选取矩形混凝土地下结构，高10 m，宽12 m，壁厚1 m，其材料参数见图3。为了考虑一般性，分别取II类、IV类两种场地，II类场地土层厚度为25 m和80 m，IV类场地土层厚度为80 m，其中土层参数见图3。其中“()”内表示IV类场地土层性质。25 m厚土层的结构埋深分别是5 m和10 m；80 m厚土层结构埋深分别为5 m、25 m和45 m。土体及结构假定为线弹性，阻尼比采用0.05。基岩处地震波采用Elcentro波，如图4所示，峰值加速度调整为0.097g。以时间历程法为基准，校核反应加速度法、反应位移法、修正反应位移法的精度。

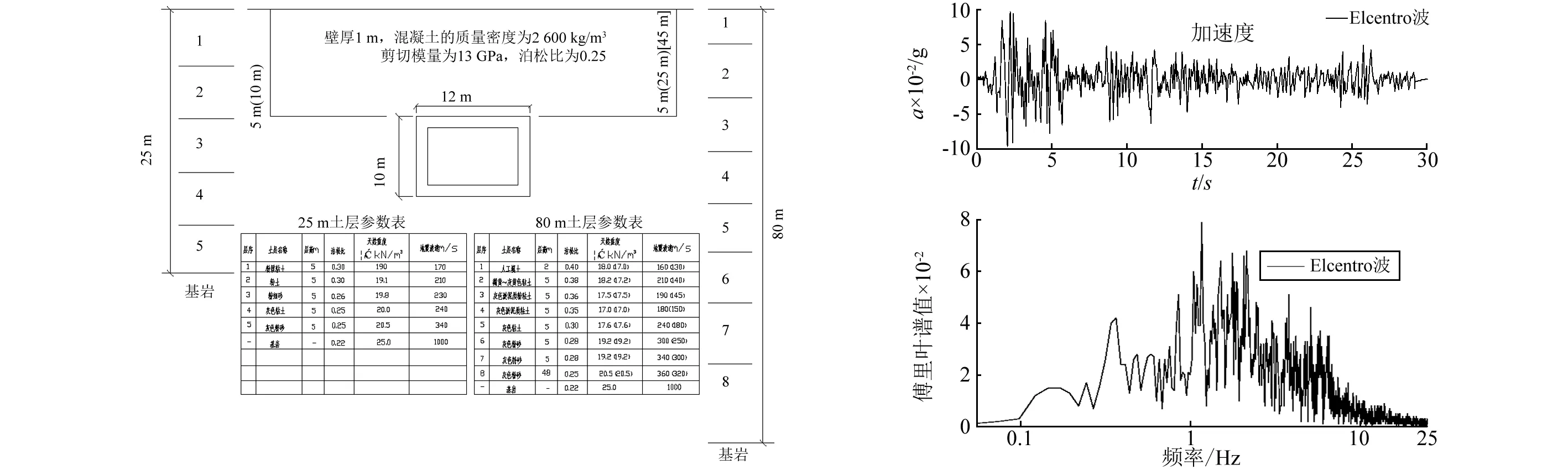
图3 车站横截面及土层参数 图4 地震动参数Fig.3 The cross section of station and soil parameters Fig.4 Ground motion parameters

2.2 计算模型

时间历程法、反应加速度法、修正反应位移法模型中，土体采用平面应变单元，地下结构采用梁单元，土体与地下结构不考虑滑移和脱离。由于基岩剪切波速较大，模型底部考虑为约束；其中时间历程法和反应加速度法模型侧向边界竖向约束、水平自由，时间历程法(采用ANSYS建模)侧向边界取离模型中心5 000 m处，以减少边界的影响，其模型见图5，反应加速度法侧向边界取离模型中心60 m处；修正反应位移法侧向边界约束，侧向边界距离中心60 m。竖向网格尺寸取为1 m，反应加速度法和修正反应位移法水平网格尺寸也取为1 m，但时间历程法水平网格尺寸有变化，变化处有过渡网格，如图5。时间历程法采用振型叠加法，取模型前300阶振型，振型阻尼比取为0.05。

图5 时间历程法模型Fig.5 Model of the time history method

反应位移法地下结构采用梁单元，周围土层采用弹簧单元模拟，弹簧刚度采用静力有限元模型计算。反应加速度法、反应位移法和修正反应位移法采用SAP2000建模，需要的土层反应采用一维场地反应分析，将土层厚沿深度划分，分层厚度取1 m，利用ProShake软件计算，土层的阻尼比取为0.05，土层为线弹性。

2.3 计算结果

四种方法的计算结果见表1～表3，只考虑地下结构侧板上端C点和侧板下端D点的内力，以时间历程法(法1)为基准，校核反应加速度法(法2)、反应位移法(法3)和修正反应位移法(法4)的精度，表中的误差为三种方法相对时间历程法的相对误差。其中时间历程法结果是结构顶底相对位移差最大时刻的截面内力。

从计算结果可知，反应位移法精度的变化规律：埋深小时比埋深大时高，埋深小时相对误差仅有1%，埋深大时的相对误差近60%；IV类场地时比II类场地高；在土层厚度较小(例如25 m)时，结构内力相对误差随埋深增加(5 m到10 m)变大(8%到42%)；在土层较厚的II类场地(例如80 m)时，侧板下端内力相对误差随埋深增加(5 m到25 m到45 m)时变大(7%到57%)，但最大相对误差出现在中等埋深时(25 m)；侧板上端内力相对误差最大值出现在埋深最小时(5 m时达62%)；在土层较厚的IV类场地(例如80 m)时，内力相对误差随埋深增加(5 m到25 m到45 m)时逐渐变大(1%到53%)，只有侧板下端的剪力和轴力最大相对误差出现在中等埋深浅时(25 m)。

表1 25 m厚土层的框架内力误差

表2 80 m厚土层的框架侧板下端内力误差

表3 80 m厚土层的框架侧板上端内力误差

修正反应位移法和反应加速度法有类似的规律：在土层厚度较小(例如25 m)时，结构内力相对误差随埋深增加(5 m到10 m)变大(1%到12%)，但侧板上端轴力正好相反；在土层较厚的II类场地(例如80 m)时，侧板下端内力相对误差随埋深增加(5 m到25 m到45 m)时变小(12%到1%)，但最小相对误差出现在中等埋深时(25 m)；在土层较厚的IV类场地(例如80 m)时，侧板下端内力相对误差都不是很大(个别大的也小于10%)，侧板上端内力相对误差随埋深增加(5 m到25 m到45 m)时变大(1%到14%)，但最大相对误差出现在中等埋深时(25 m)。

3 结 论

虽然反应加速度法和反应位移法在理论上随结构埋深没有精度变化的问题，但数值算例表明有精度变化的问题，因此本文以时间历程法为基准，评价地下结构埋深变化时的反应加速度法、反应位移法、修正的反应位移法的精度，得出了下列结论：

(1)场地类别、土层厚度、结构埋深都会影响三种方法的精度。

(2)整体上看，修正的反应位移法、反应加速度法的精度比反应位移法高。

(3)反应位移法在埋深较小、土层较软时精度尚可接受，埋深较大时，精度较差；而反应加速度法和修正的反应位移法在不同埋深和土层时精度都较高。

[1] 刘如山，胡少卿，石宏彬．地下结构抗震计算中拟静力法的地震荷载施加方法研究[J]．岩土工程学报，2007，29(2)：237-242．

LIU Rushan, HU Shaoqing, SHI Hongbin. Study on seismic loading of pseuo-static approach used in the seismic design of underground structure[J].Chinese Journal of Geotechnical Engineering, 2007,29(2):237-242.

[2] 董正方,王君杰,姚毅超.深埋盾构隧道结构抗震设计方法评价[J].振动与冲击,2012,31(19):79-85.

DONG Zhengfang, WANG Junjie, YAO Yichao. Evaluation of seismic design methods for a deeply-buried shield tunnel[J]. Journal of Vibration and Shock ,2012,31(19):79-85.

[3] NISHIDA M, MATSUI T. Applicability of seismic deformation method to aseismic analysis of underground linear structure[C]// 14th International Offshore and Polar Engineering Conference. 2004: 600-606.

[4] TATEISHI A．A study on seismic analysis methods in the cross section of underground structures using static finite element method[J]. Structural Engineering/Earthquake Engineering of JSCE, 2005, 22(1): 41-53.

[5] 片山幾夫，足立正信，嶋田穰, 等．地下埋設構造物の実用的な準動的解析手法「応答震度法」の提案[C]// 土木学会年次学術講演会講演概要集. 1985：737-738．

[6] 商金华，杨林德．软土场地地铁车站抗震计算的等代地震加速度法[J]．华南地震，2010，30(1)：6-15.

SHANG Jinhua, YANG Linde. Equivalent static method of seismic calculation for subway station in soft site[J]. South China Journal of Seismology, 2010, 30(1):6-15.

[7] 刘晶波，王文晖，赵冬冬，等．地下结构抗震分析的整体式反应位移法[J]．岩石力学与工程学报，2013，32(8)：1618-1624．

LIU Jingbo, WANG Wenhui, ZHAO Dongdong, et al. Integral response deformation method for seismic analysis of underground structure[J].Chinese Journal of Rock Mechanics and Engineering, 2013,32(8):1618-1624．[8] 陶连金，王文沛，张波，等．地铁地下结构抗震设计方法差异性规律研究[J]．土木工程学报，2012，45(12)：170-176．

TAO Lianjin, WANG Wenpei, ZHANG Bo, et al. Difference law study of seismic design methods for subway structures[J].China Civil Engineering Journal,2012,45(12):170-176.

[9] CLOUGH R W, PENZIEN J. Dynamics of structures[M]. 3rd ed. Berkeley,USA: Computers & Structures, Inc,2003.

[10] 刘晶波，王文晖，张小波，等．地下结构横断面地震反应分析的反应位移法研究[J]．岩石力学与工程学报，2013，32(1)：161-167．

LIU Jingbo, WANG Wenhui, ZHANG Xiaobo, et al. Research on response deformation method in seismic analysis of underground structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2013,32(1):161-167.

Accuracy of the response acceleration method and response displacement method considering different imbedding depths of underground structures

DONG Zhengfang1, CAI Baozhan1, YAO Yichao2, LI Fengli1, ZHU Hongyun1

(1. Institute of Materials and Structures, Henan University, Kaifeng 475004, China；2. CREEC East China Survey and Design Co., Ltd., Hangzhou 310004, China)

The conclusion that the accuracy of the response acceleration method (RAM) and response displacement method (RDM) is unchange with different imbedding depths of underground structures is only based on the theoretical equations of the above two methods. The performances of three methods, the RAM, RDM and modified response displacement method (MRDM), were evaluated and compared with that of the dynamic time history method through a selected benchmark numerical example.The internal forces in the underground structure were computed in different geological conditions and with different depths. It is found that if the time history method is selected as a benchmark, the RAM, RDM and MRDM are affected by the site classification, soil thickness and embedment depth. The RAM and MRDM are generally superior to the RDM. It is also found that the RAM and MRDM are slightly affected by the embedment depth and RDM is only suitable for shallow underground structures.

response acceleration method;response displacement method; underground structure; seismic design

国家自然科学基金资助项目(51408195)；河南省教育厅科学技术研究重点项目(14B560031)；河南大学科研基金项目(2013YBZR002)

2016-01-08 修改稿收到日期： 2016-05-25

董正方 男，博士，讲师，1980年生

TU311.41；TU93

A

10.13465/j.cnki.jvs.2017.14.034