基于多弦模型的轨道短波不平顺测量研究

殷 华， 朱洪涛， 王志勇， 吴维军， 金哲民

(1.南昌大学 机电工程学院，南昌 330096; 2.江西农业大学 软件学院，南昌 330045)

基于多弦模型的轨道短波不平顺测量研究

殷 华1 , 2， 朱洪涛1， 王志勇1， 吴维军1， 金哲民1

(1.南昌大学 机电工程学院，南昌 330096; 2.江西农业大学 软件学院，南昌 330045)

弦测是目前铁道工务中对钢轨不平顺检查广泛使用的一种手段，但理论上的缺陷制约了其对较短波长的响应。在分析中点弦测法频域特性的基础上，提出了多弦测量理论及数据补偿方法。根据不平顺波段的不同找到合适的弦长组合避免了幅值增益为零；利用傅里叶变换在频域对测量结果进行补偿可得到原始值。数据仿真及实际线路测试结果表明,该方法能够准确的计算出轨道短波不平顺幅度，适合工程中的应用。

中点弦模型；轨道短波不平顺；频域分析；弦测法

铁路轨道短波不平顺是指由于长期受到机车的碾压、冲击在钢轨顶面高低方向出现的不平顺病害，通常其波长都在30～1 000 mm，深度在50 μm～1 mm。为了剖析短波不平顺产生的原因，国内外学者们进行了深入广泛的研究，但轨道短波成因比较复杂，与机车行驶的速度、载重、轨道的类型、所处的位置等多个因素有关，国内外虽对于短波产生机理尚未达成共识，但一致认为铁路轨道短波不平顺病害可引起轨道和车辆轮架的激烈振动，影响车辆的使用寿命，在严重时候还会造成脱轨，给人民群众的生命财产造成巨大的损失[1-5]。如何早期检测出短波不平顺病害并予以消除成为当前铁路工务的重点。由于铁路轨道自建成起就固定在路基上，因此对其的测量仅能通过间接的手段进行，目前国内外主要有动态的惯性法和静态的弦测法：惯性法常运用在大型轨检车上，其原理是当列车在轨道上高速通行时其轴箱会产生振动，幅度与不平顺密切相关，通过测量该振动的加速度并进行二次积分得到不平顺值；如：Rail measurement公司的RCA波磨车、钢轨磨耗动态检测系统RCIU-1[6]等；弦测法通常采用的是平直尺或塞尺，其原理是用一根定长(常为1 m)的刚性直尺放在轨道顶面形成一根弦，通过接触或非接触手段采集弦上各点与轨道表面之间的间隔得到不平顺值。惯性法测量成本高而基于平直尺的弦测法依靠手工测量效率低下，这两种方法各有缺点，同时动、静检查一般都不具有一致性[7]且平直尺测量短波其基准为定长的弦，只能给出不平顺点的相对值，无法真实反应整个轨道的不平顺尺度，因此不适合当前铁路工务对轨道病害快速精测和现场复核的需要。轨道检测小车是当前广泛使用的一种推行测量设备，其采用的中点弦测模型通过多年的发展与改进，它的中、长波检测精度与效率完全满足现场测量需要，但由于原理所限，对轨道短波不平顺的测量一直未能取得令人满意的效果[8-9]。本文以中点弦测模型为基础，结合轨道短波的特点，提出了基于多弦理论的轨道短波不平顺测量和数据补偿方法，实现以轨道检测小车为基本结构的轨道短波不平顺快速测量系统。

1 中点弦测量方法及特性

文献[10]规定：轨道不平顺静态评价需采用10 m弦的中点矢量。但10 m弦设备过于庞大，实际工务中均采用短弦测量，利用文献[11]所提出的“以小推大”模型来计算10 m弦的中点矢量。

(1)

式中：G(X)为轨道不平顺函数；L表示测量弦长；△表示中点矢量测量值。

对式(1)进行傅里叶变换可以得到其传递函数

(2)

式中：ω=2π/λ为空间角频率；λ为轨道不平顺波长。从式(2)可知，经过中点弦测量后，轨道不平顺波形的相位偏移为零，幅值和测量弦长度及被测轨道的不平顺波长有关。

图1是目前广泛采用的750 mm测量弦长时检测小车幅值增益-波长响应曲线。当测量弦长是被测轨道不平顺波长的2k(k=0,1,…)倍时，幅值增益响应为零。即随着波长的变短，幅值增益响应接近于零或等于零的点不断增多，当这些数据带入到“以小推大”模型递推时，累积误差将使测量结果偏离实际值，严重影响测量精度。虽然测量弦长的缩短这种情况会有所改善，但却无法避免对测量精度的影响，并且过短的弦长会造成机械加工上的困难，在实际工程中毫无意义。

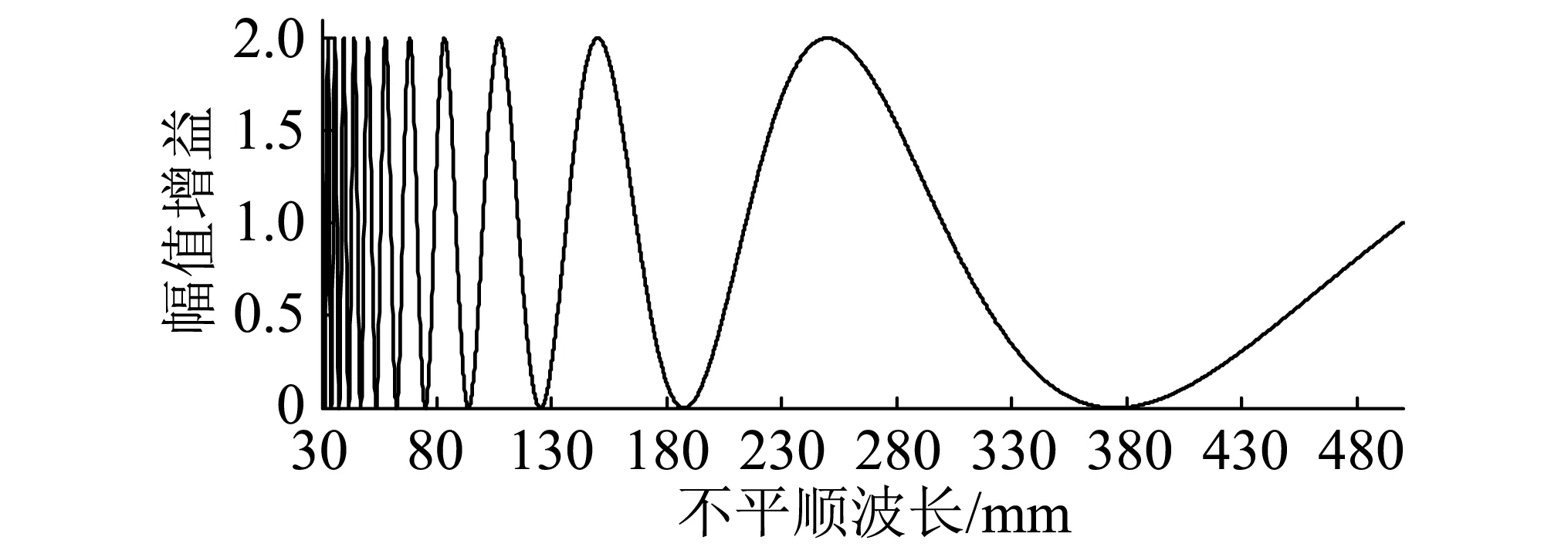
图1 750 mm弦长中点弦测法幅频特性曲线Fig.1 Midpoint chord amplitude-frequency curve at 750 mm length

文献[12-13]在此基础上提出了偏弦和多点测量模型，试图构建不同的传递函数来解决该问题，但这两种方法只能尽量减少而不能消除幅值增益为零的点，且都会带来相位上的偏移，影响后续对超限点的现场复核。

2 多弦测量理论

2.1 模型

根据上面分析，当测量弦长一定时，随着被测不平顺波长的变短幅值增益曲线为零的点逐渐增多，无法准确的获取所需的数据，这也是当前弦测法不能测量短波的原因所在。但由于中点弦测模型相位不存在着偏移，而不同长度的弦长在测量同一轨道时幅值增益为零点的位置是不相同，那么采用多个中点弦叠加测量则有可能得到变化相对平缓且不存在零点的幅值增益-波长响应曲线。设Ln(n=1,2,…,k)表示各测量弦的长度,Σ表示多中点弦测量下对同一不平顺点的测量值之和，则

(3)

对式(3)进行傅里叶变换得到多中点弦测量下幅频响应函数：

(4)

条件1不存在为零的点且极小值点Hmin尽可能大。

条件2方差S2在所有弦长组合的取值中最小。

“条件1”保证了对区间内的各种波长均有响应且具有一定的测量精度。而“条件2”则使得在整个波长区间内幅值增益曲线较为平坦，在后续补偿数据时为短波不平顺中较长的波长成分提供同样准确的复原结果。

2.2 参数优化

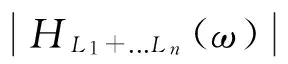
表1 不同弦数量下的最优弦长

图2 多中点弦测量幅频特性曲线Fig.2 Multi-midpoint chord amplitude-frequency curve

2.3 基于频域的逆滤波方法

从本质上来说，中点弦测法实际上是一种特殊的滤波器，不论采用何种弦长的组合，除个别点外其所测得到的值相对于原始轨道不平顺始终会存在着夸大或缩小，但其空间频率不变。傅里叶变换是频率分析中常用的方法，理想情况下对测量数据进行傅里叶变换即可得到其所包含的空间频率(波长)信息，再根据其幅频增益曲线对测量数据进行补偿，可恢复轨道的原始不平顺值。为了说明上述方法，设当前轨道长度为30 m，包含有波长为330 mm的周期不平顺，幅值为0.1 mm，利用弦长290 mm的中点弦测量，采样间隔为4 mm，截取其中8 192个数据进行傅里叶变换得到，如图3所示。根据傅里叶变换的性质，330 mm的波长并不能对应于一个整数频率点，并且在进行数据截取的时候也不是整数个周期，所以在傅里叶变换后将会出现“泄漏”，表现在图中即为在频率点3.021处有一个尖峰，对应的幅度为0.154 9，而在其两侧还有多个频率泄漏造成的小的尖峰。由于傅里叶变换后的各个空间频率点对应的不平顺波长并不是线性的，在分辨率较低的相对长波部分幅值增益曲线较为平坦，且这些泄露的尖峰幅值较小，在实际轨道中的不平顺通常也不是标准的周期波形，各个频率之间泄漏会互相抵消，因此对最终结果所造成的误差影响较小。利用图3的数据结合式(2)，对各个空间频率的幅值进行补偿后再进行傅里叶反变换即可得到原始轨道的不平顺值，去掉头尾各5 m的波形后取其中部分绘制，如图4所示。从图4可知，幅度补偿后的恢复值与原始值基本一致，误差最大处也不超过0.01 mm与原始值相差一个数量级。相关系数通常用来表征两个序列之间的近似程度，对原始值与复原值求相关系数r=0.992 3，说明两者为强相关。因此，该方法是可行的。

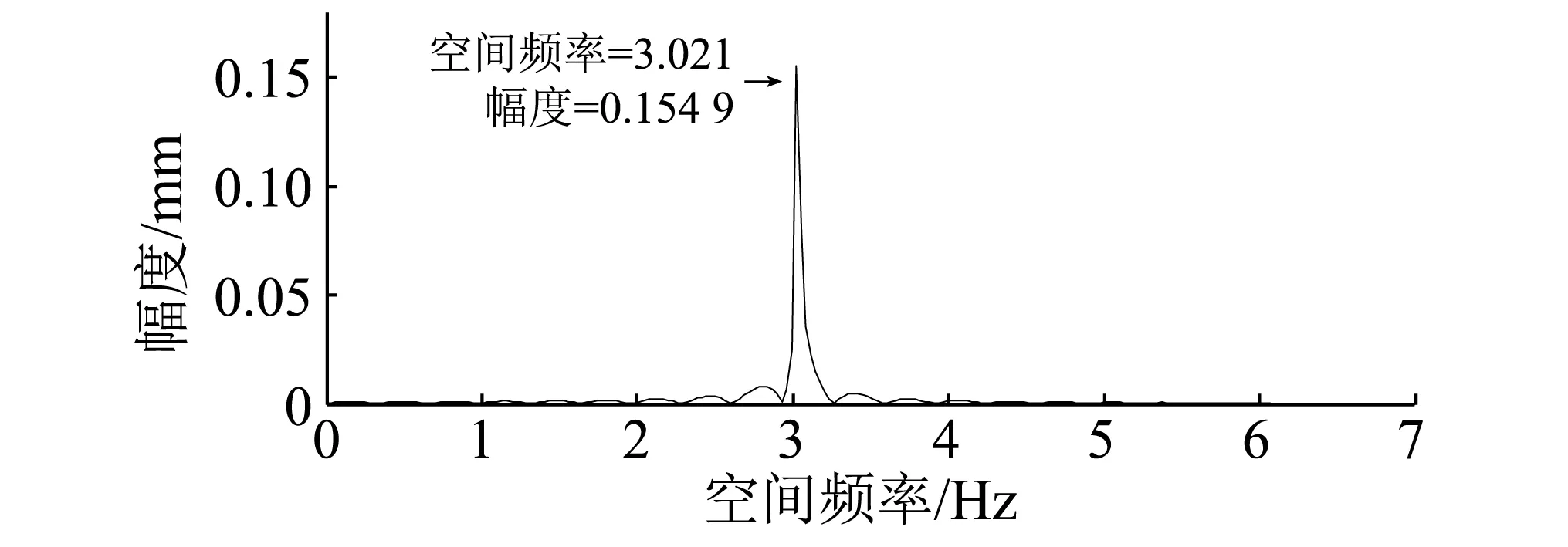
图3 频域特性Fig.3 The frequency-domain characteristics

图4 部分复原数据Fig.4 The part of restore waveform

综上，可得出基于多弦理论的轨道短波不平顺测量方法：

步骤1 根据感兴趣的波段(如波长范围在30～1 000 mm之间)结合幅值增益-波长响应曲线及最终设备的成本、精度等多个方面选定合适的弦长数量及各弦的长度对轨道进行多中点弦测量。

步骤2 对测量结果进行傅里叶变换，滤除感兴趣的波段以外的数据后，根据选定弦长的波长-幅值增益曲线得到各不平顺波长的增益值并对滤波后的数据进行逐点补偿，显然，在频域的点越多补偿精度越高，但同时计算量也会增大。

步骤3 对补偿后的数据进行傅里叶反变换并叠加得到原始不平顺值。

3 仿真计算与分析

上述分析均是基于理论，下面利用MATLAB在理想环境下对多弦理论的正确性进行验证。通常轨道不平顺的成分较为复杂，因此可设某轨道的长度为30 m，包含有12个的正弦不平顺，波长λ分布在小于30 mm，30～1 000 mm，>1 000 mm三个区间，分别为{18 mm, 26 mm, 86 mm, 145 mm, 230 mm, 457 mm, 467 mm, 667 mm, 780 mm, 890 mm,1 100 mm,1 260 mm}，各个正弦不平顺的幅度及相位随机生成，但合成后的轨道不平顺峰峰值不超过0.4 mm，图5是该合成轨道在0～5 m之间的不平顺波形。采用“2.2”中计算得到的L1=173 mm和L2=290 mm构成测量双弦，以4 mm为采样间隔对该轨道进行等距空间采样。

图6是双中点弦测量数据之和。通过与图5对比可知，经过双弦测量所得的轨道不平顺幅值与原始不平顺有较大差异，但在同一个轨道里程点上不平顺的形状基本一致。这也从另外一个侧面说明了中点弦测法具有相位不变，幅值增益随测量弦长和不平顺波形变化的特点。对图6进行傅里叶变换,并利用“2.3”中频域逆滤波方法对其进行数据处理可得到双弦测量轨道不平顺的复原值。为了便于观察复原精度，将复原值与原始值相减可得图7。从图7可知，在轨道的起始部分复原值与原始值相差较大，这主要是因为测量弦本身具有一定的长度，弦测值的起始点与轨道本身的起始点有偏移。随着测量里程的不断增加这种差异逐渐减小，当轨道里程超过2 m后，复原值与原始值之间最大相差0.008 mm，并且随着轨道里程的增加这个差值还会逐渐减小，可达微米级。

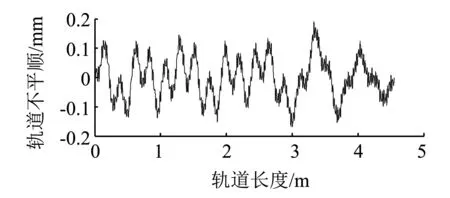
图5 模拟轨道不平顺波形(部分)Fig.5 The part of simulation of track irregularity

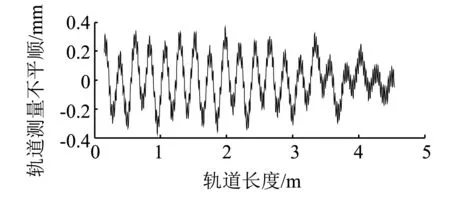
图6 双弦测量的轨道不平顺波形(部分)Fig.6 Measured value of irregularity under double chord

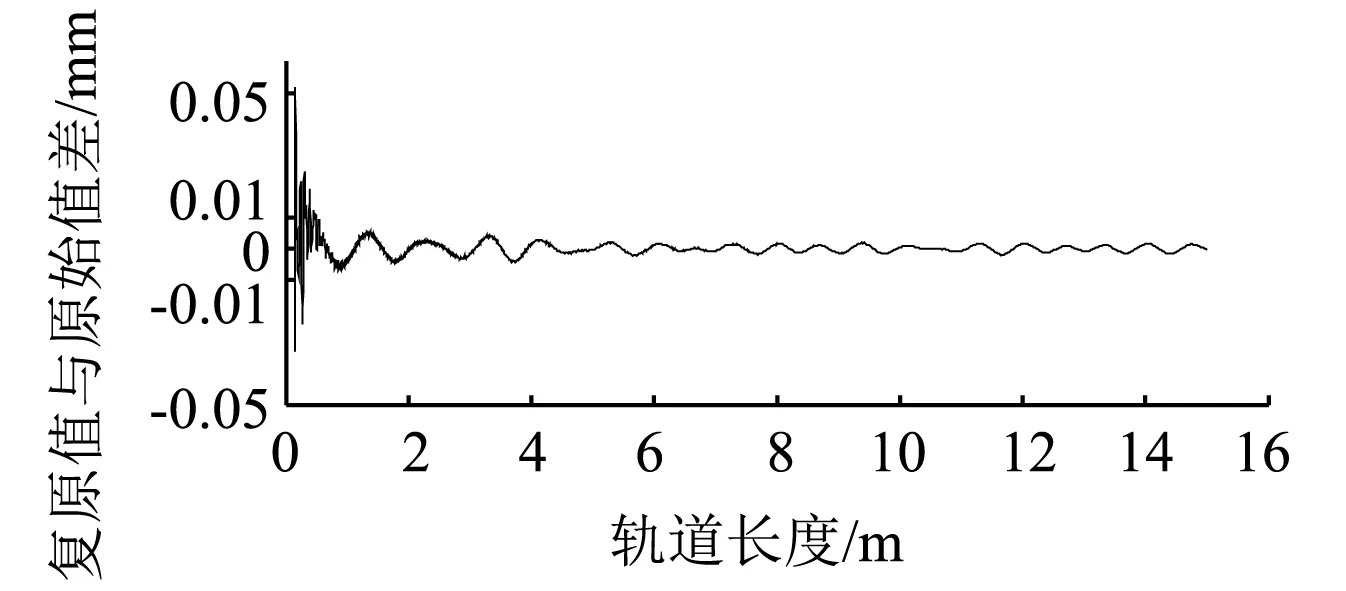
图7 复原波形与原始波形差值(部分)Fig.7 The difference between restore and original waveform

为了比较多弦法和单弦法的优劣，对上述模拟的不平顺轨道分别用290 mm单弦和173 mm单弦测量后进行傅里叶变换，并与双弦测量数据在频域对比得到图8，图8(a)为双弦测量数据分析结果，可以很容易看出该数据中包含有多种频率，特别是含有空间频率为6.9 Hz和11.6 Hz的两个成份；图8(b)是采用290 mm单中点弦对同一目标的测量的结果，在该图中11.6 Hz的成份依然存在但频率为6.9 Hz的部分却消失了，经过计算可知该成份对应的波长约为145 mm，而290 mm的中点弦对该波长的响应为0；图8(c)是采用173 mm弦的测量结果，图中6.9 Hz的成份存在而波长为86 mm对应的11.6 Hz频率成份却消失了，这恰好是173 mm中点弦幅值响应近似为0的波长。仿真计算结果表明：相对于单弦测量，经过计算的多弦组合能够对各个频率的波长均有响应且复原精度完全满足当前铁路工务中对短波测量的要求。

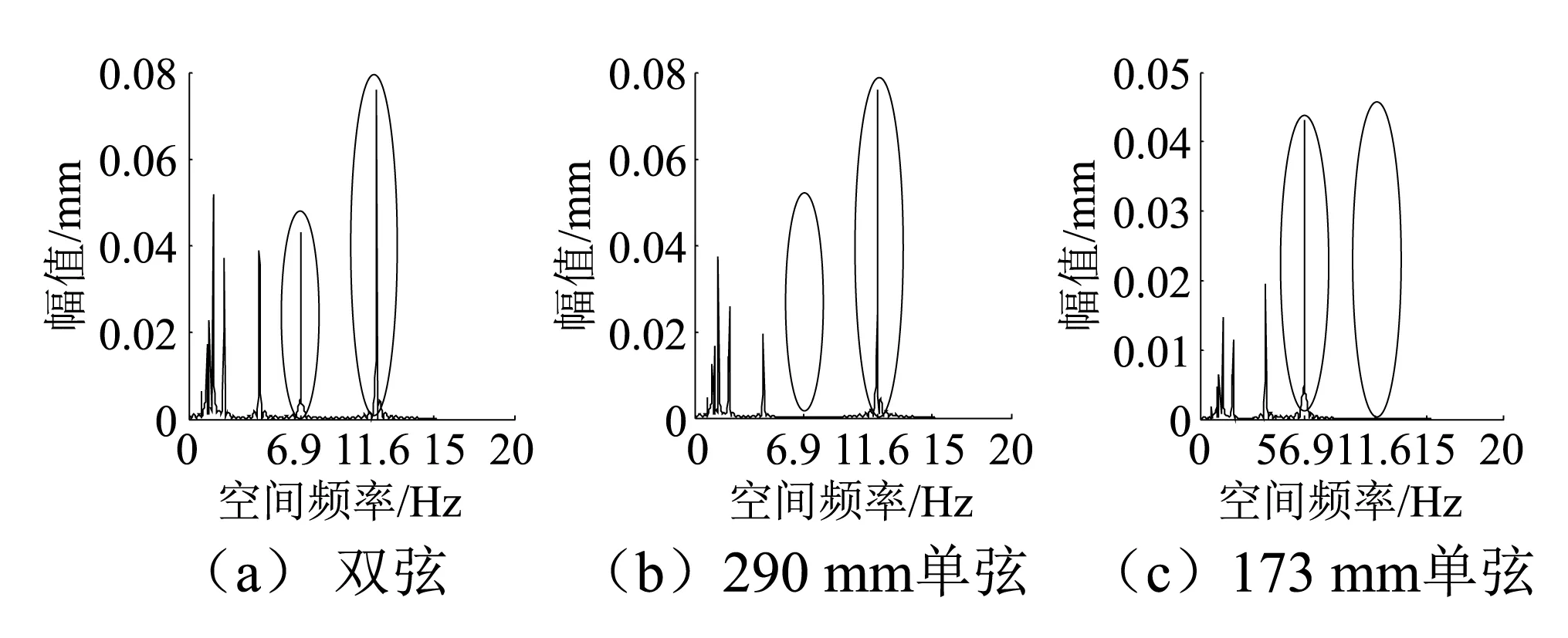
图8 单弦测量与多弦测量频域对比Fig.8 Comparison of different chord measuremnt value on frequency-domain

4 轨道短波不平顺实测

在实际轨道线路中包含了大量的噪声及诸多不确定因素，为了检验多弦理论的测量效果，选取自备的轨道线路进行线路实测。实验线路长度约为10 m，线路中包含有未知波长的成分，采用平直尺测量该段线路并滤波得到波长在30～1 000 mm之间的不平顺峰峰值约在0.1 mm。出于成本考虑，利用5个激光传感器布置成L1=173 mm和L2=290 mm的双弦结构，传感器型号为基恩士IL-100，精度为0.01 mm。安装于轨道检查小车后如图9所示。轨道检查小车走行轮安装有编码器，控制其每4 mm触发采样一次，数据送入到上位机软件记录并处理。

图9 测量装置结构Fig.9 Measuring device structure

图10是里程在0～4.5 m之间采用双弦测量的数据曲线，图中不平顺峰峰值最大可达到约0.3 mm，但该值是多个不平顺波长成份在中点弦测模型下的幅值放大或缩小之和。对该数据进行傅里叶变换得到图11所示部分单边谱,这反映出当前实测轨道的波长成分都<200 mm(空间频率为5 Hz)。在滤除<30 mm波长(空间频率为33.3 Hz)及>1 000 mm波长(空间频率为1 Hz)成份后，对照图2双弦测量的幅值增益曲线，找到相应的增益值进行逆滤波。由于测量原理的不同，在里程为1 m之前平直尺测量数据与双弦法不具有可比性，因此对比从里程1.5 m开始，图12(a)为时域对比，可以看出在总体趋势上，两者数据保持一致，此时该轨道不平顺的峰峰值最大<0.2 mm，约为0.1 mm,符合实际线路状态。图12(b)为频域对比，图中两种测量频率成份基本保持一致。但在细节上，双弦法测量数据与平直尺数据还有一定的差异，究其原因主要是由于平直尺和双弦法测量的采样间距不同(分别为5 mm和4 mm)，以及两次傅里叶变换过程中的频率泄露和传感器安装、机械结构的误差造成的，但这种差异通常极小，在本例中除个别突变点外最大也不超过0.02 mm，不影响实际工程中对线路整体情况的判断。

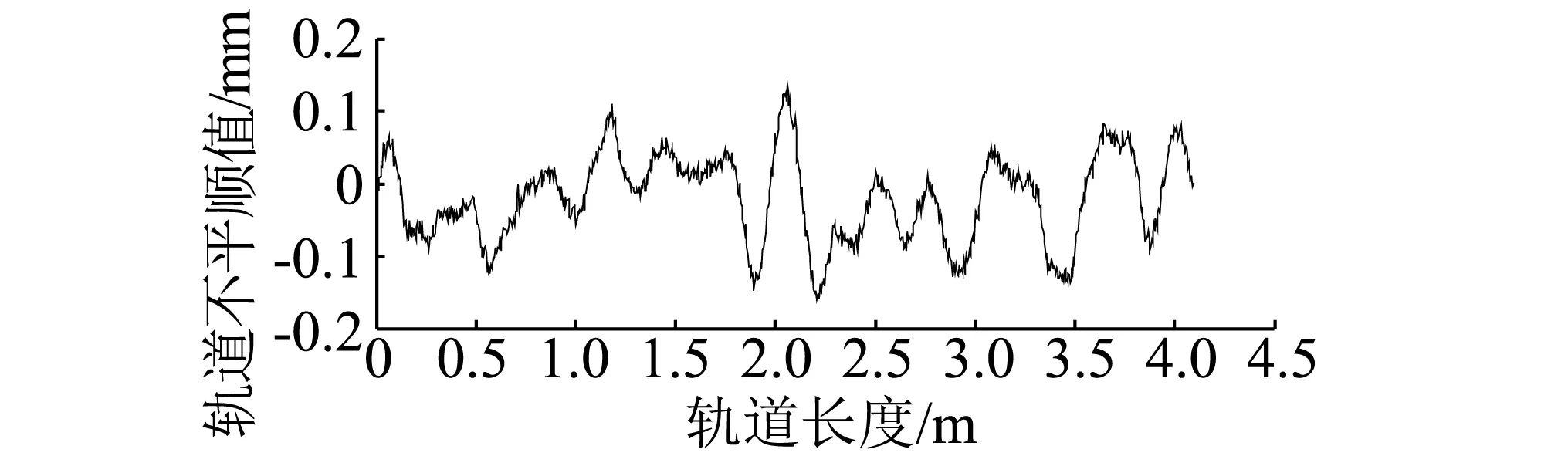
图10 实际轨道双弦测量值Fig.10 Double chord measuremnet value on track

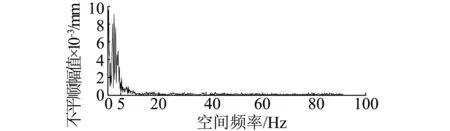
图11 实际轨道双弦测量频域特性Fig.11 The frequency domain characteristics of track

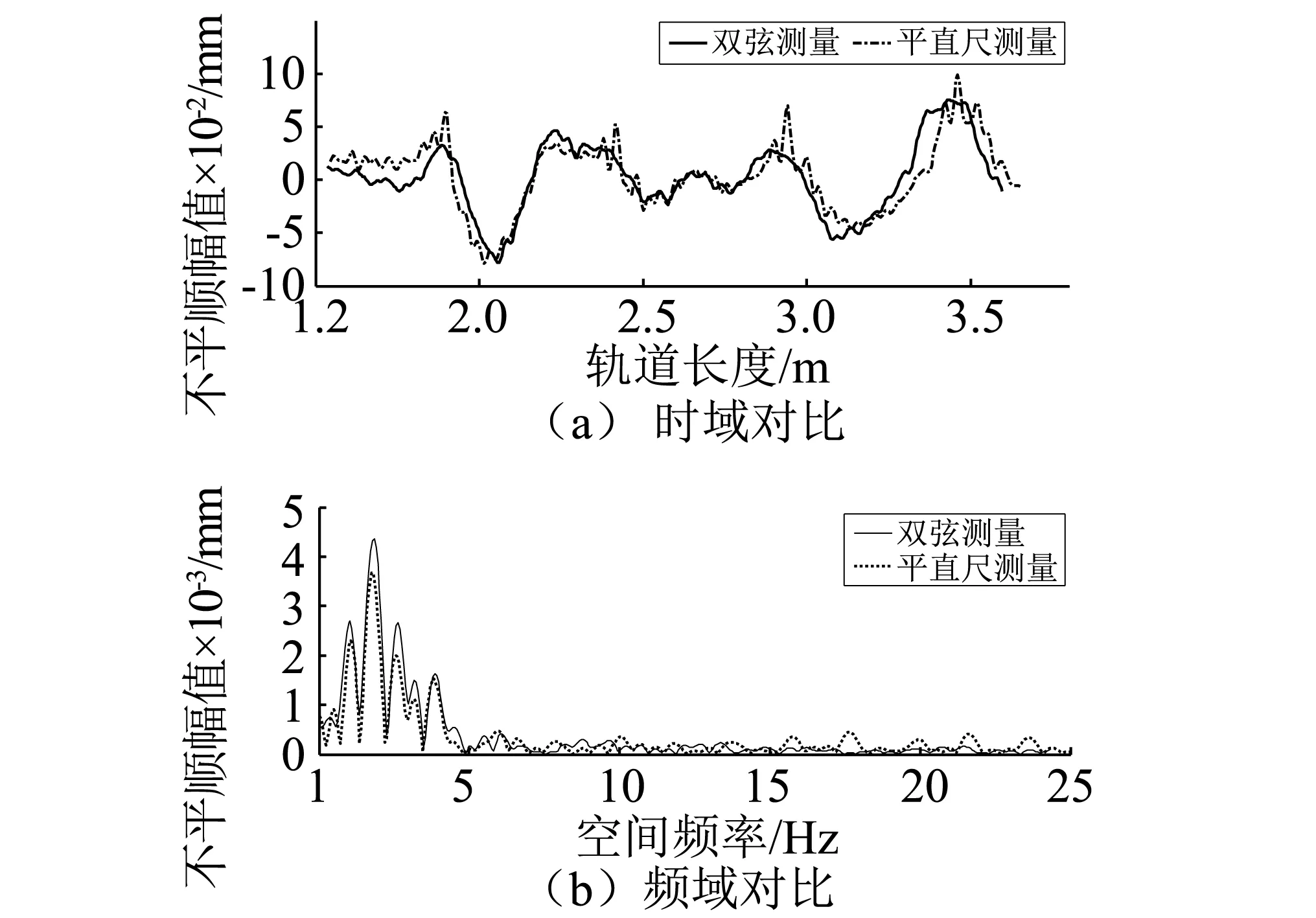
图12 实际轨道复原值与平直尺对比Fig.12 Comparison of the restore waveform with the straight ruler test value

5 结 论

受基本理论的制约，对如何使用基于弦测法的设备测量波长较短的轨道不平顺一直是受业界广泛关注的问题。在分析弦测法优势及缺陷的基础上得到以下结论：

(1)相较于单弦测量，多弦测量能够避免幅值增益为零的问题。这使得弦测法对轨道上各种波长的不平顺都有响应。

(2)根据所感兴趣的不平顺波段的不同，系统弦的数量及弦长的组合等参数应有所不同。数据仿真及实际线路测试证明选择合适的参数能够很好的获得轨道短波不平顺量值。

(3)按照多弦理论模型的特点，在工程应用中需注意所选传感器及其安装位置的精度，这将直接影响模型的幅频和相频特性，对复原波形造成幅值及位置上的偏差；由于傅里叶变换的频率分辨率与选取的点数相关，但过多的点数又会对工程中数据处理的实时性产生影响，故应该结合整个系统的性能和所要求的测量精度综合考虑。

[1] GRASSIE S L, KALOUSEK J. Rail corrugation: Characteristics, causes, and treatments[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit, 2009, 223(6):581-596.

[2] 单涛涛,楼梦麟,贾宝印.关于上海地铁一号线轨道高低不平顺问题的探讨[J]. 振动与冲击,2012,31(12):53-58. SHAN Taotao,LOU Menglin,JIA Baoyin.Preliminarily exploring a problem of track vertical profile irregularity of Shanghai metro line 1[J].Journal of Vibration and Shock, 2012,31(12):53-58.

[3] 谷爱军,刘维宁.国外城市轨道交通钢轨波浪形磨耗病害研究及治理[J]. 城市轨道交通研究,2011,14(12):51-55. GU Aijun,LIU Weining. Study and control of rail corrugation defects of urban rail transit in foreign cities[J]. Urban Mass Transit,2011,14(12):51-55.

[4] 崔晓璐,钱韦吉,张青,等.直线线路科隆蛋扣件地段钢轨波磨成因的理论研究[J].振动与冲击,2016,35(13):114-118. CUI Xiaolu,QIAN Weiji,ZHANG Qing,et al.Theoretical study on the generation mechanism for rail corrugation of a tangential track supported by Cologne-egg fasteners[J]. Journal of Vibration and Shock, 2016, 35(13): 114-118.

[5] VUONG T T, MEEHAN P A, EADLE D T, et al. Investigation of a transitional wear model for wear and wear-type rail corrugation prediction[J].Wear,2011,271(1/2):287-298.

[6] 刘伶萍,杜鹤亭,杨爱红.钢轨波浪磨耗检测系统的研究开发[J].中国铁道科学,2002,23(6):65-69. LIU Lingping,DU Heting,YANG Aihong. Development of rail corrugation inspection system[J].China Railway Science,2002,23(6):65-69.

[7] 魏晖,朱洪涛,刘荣平,等.无砟轨道轨向动静态轨向数据的差异性的时频域解释[J]. 科学技术与工程,2013,13(17): 5040-5045.

WEI Hui,ZHU Hongtao,LIU Rongping, et al.New insights into the alignment data bias between kinematical measurment and static measurement for ballastless track[J]. Science Technology and Engineering,2013,13(17):5040-5045.

[8] 杜鹤亭.长波长轨道不平顺检测中的数字滤波方法[J]. 中国铁道科学,2000,21(4):58-65. DU Heting. Digital filtering method for long wave track irregularity inspection[J].China Railway Science,2000,21(4):58-65.

[9] 朱洪涛,魏晖,熊瑞文,等.弦测法检测轨向不平顺的研究[J].铁道建筑,2005(10):63-64. ZHU Hongtao,WEI Hui,XIONG Ruiwen,et al. Discussion on method of chord measuring for track alignment irregularity[J].Railway Engineering,2005(10):63-64.

[10] 高速铁路无砟轨道线路维修规则(试行)：TG/GW 115—2012[S].北京:中国铁道出版社,2012.

[11] 朱洪涛,魏晖,王志勇,等.轨检仪弦测法“以小推大”检查轨道轨向不平顺的理论研究[J]. 铁道学报,2007,29(1):36-40. ZHU Hongtao,WEI Hui,WANG Zhiyong, et al. Discussion on inspection of track alignment irregularities according to method of chord measuring and its“using small fetch big”[J]. Journal of the China Railway Society, 2007, 29(1):36-40.

[12] 程樱,许玉德,周宇.三点偏弦法复原轨面不平顺波形的理论及研究[J].华东交通大学学报,2011(1):42-46. CHENG Ying,XU Yude,ZHOU Yu.Theory and research of asymmetrical chord offset method of restoring a wave form of track iregularity[J].Journal of East China Jiaotong University, 2011(1):42-46.

[13] 毛晓君.基于弦测法的轨面短波不平顺检测理论与方法[D].上海:同济大学, 2014.

Rail short-wave irregularity measurement based upon a multi-midpoint chord model

YIN Hua1,2, ZHU Hongtao1, WANG Zhiyong1, WU Weijun1, JIN Zhemin1

(1.School of Mechatronic Engineering, Nanchang University, Nanchang 330096,China;2. School of Software, Jiangxi Agricultrual University,Nanchang 330045,China)

The chord measurement is a widely-used method for inspecting the track irregularity at present. But the theoretic defect restricts its response to shorter wavelength. Based on the analysis of frequency characteristics, a multi-chord measurement theory and a data compensation method were proposed. According to the irregularity band, a suitable combination of different chord lengths was found to avoid the amplitude gain to be zero. In order to get the original value, the Fourier transform was utilized to compensate the measurement data in the frequency domain. The data simulation and test results show that the method is able to calculate the rail short-wave irregularity precisely and is suitable for engineering applications.

midpoint chord model; rail irregularity;frequency domain analysis;chord measurement method

国家自然科学基金地区科学基金(51468042)；江西省自然科学基金(20142BAB206003)

2016-03-21 修改稿收到日期： 2016-06-11

殷华 男，博士生，讲师，1982年生

朱洪涛 男，硕士，教授，1962年生

U216.3；TH17

A

10.13465/j.cnki.jvs.2017.14.028