基于动力学共线刚度的空间隔振平台结构参数优化

张永亮， 郭百巍

(1. 中国电子科技集团公司第三研究所， 北京 100015；2. 北京理工大学 飞行动力学与控制教育部重点实验室， 北京 100081)

基于动力学共线刚度的空间隔振平台结构参数优化

张永亮1， 郭百巍2

(1. 中国电子科技集团公司第三研究所， 北京 100015；2. 北京理工大学 飞行动力学与控制教育部重点实验室， 北京 100081)

针对空间隔振平台的参数优化设计问题，引入一个新的评价指标——动力学共线刚度。空间隔振平台上下平台的半径和相邻铰接点所对应的圆心角被选为设计变量，以最小动力学共线刚度的最大化为目标函数，以在指定的带宽内动力学共线刚度满足工程设计要求为约束条件，建立参数优化问题的模型，并以遗传算法为优化工具进行数值求解。仿真结果表明，经参数优化后的空间隔振平台满足工程设计指标要求。

空间隔振平台；动力学共线刚度；遗传算法；优化设计

对于空间隔振平台，要想获得某些期望的性能，其结构必须进行优化设计。空间隔振平台的优化包括结构的优化和尺寸方面的优化两方面的内容，但限于其应用场合及特定目标要求，本文要研究的空间隔振平台结构上选用Stewart[1]平台结构构型，并在此基础上研究结构参数尺寸对期望性能的影响，通过某些优化算法获取最优的尺寸参数组合。空间隔振平台的优化设计既是一个多性能指标和多目标函数的优化问题，这些性能指标包括运动学和静态性能指标(各向同性[2-3]、操作数[4-5])；动力学性能指标(平衡性[6-7]、动力学各向同性[8-9]、自然频率[10]、动力学响应等[11])；精度性能和刚度性能[12-13]，同时，由于选取的目标函数不同[14]，约束函数不同或优化算法不同，使得空间隔振平台的优化问题又是一个多解的问题。

动力学共线刚度[15]是静力学刚度的扩展，它的大小取决于空间隔振平台的结构参数和质量惯性参数，其最大和最小取值可以作为优化空间隔振平台的动力学指标。

1 空间隔振平台的数学模型

空间隔振平台由基础平台、动平台和六个支腿构成，基础平台和支腿之间通过U型铰连接，动平台和支腿之间通过球型铰连接，支腿可以简化为只有弹性系数和阻尼系数的弹性振子模型。其整体结构图,如图1所示。

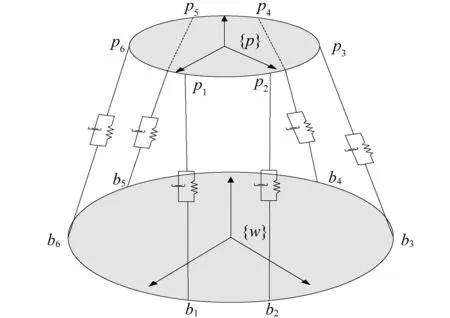
图1 空间隔振平台结构示意图Fig.1 The abridged general view of space-based vibration isolation platform

其中上、下平台各铰接点的分布图如图2所示。

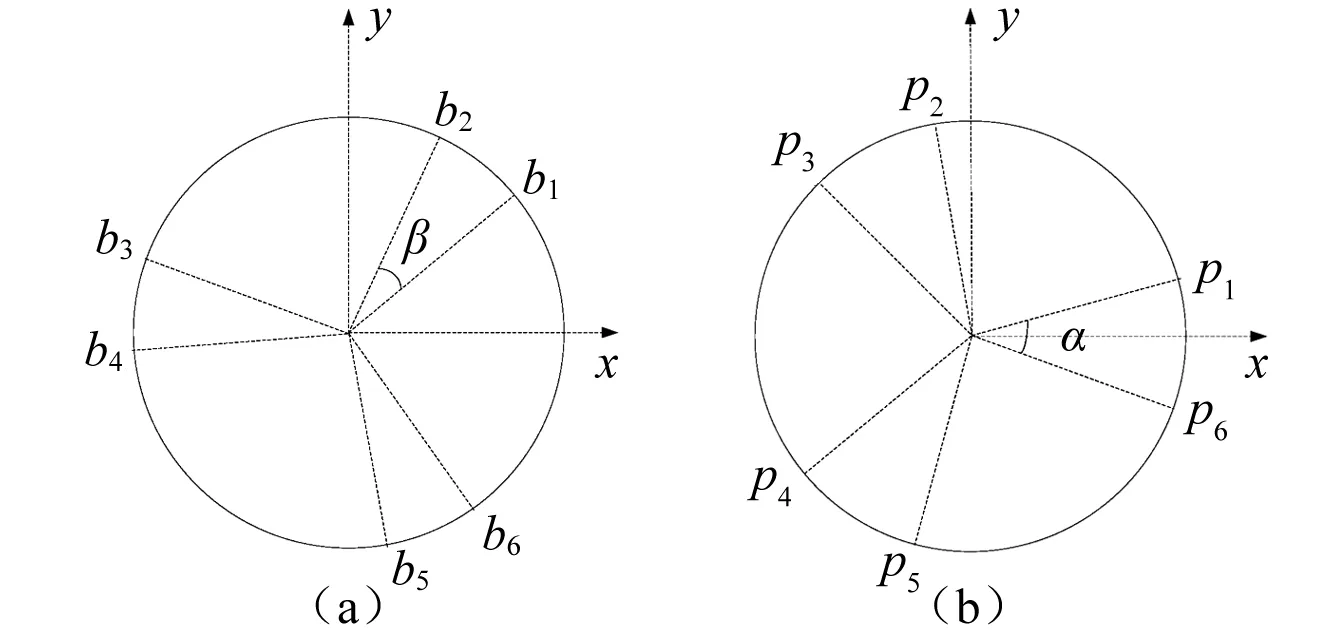
图2 上、下平台铰接点分布图Fig.2 The distribution of the connect points on the top and bottom

为了方便对空间隔振平台的模型进行数学描述，定义以下几个坐标系：

(1)坐标系{W}，坐标原点位于基础平台的质心，与基础平台固连；

(2)坐标系{P}，坐标原点位于上平台的质心，与上平台固连；

(3)坐标系{G}，全局惯性坐标系，坐标原点与动平台质心重合。

设上平台半径为rp、基础平台半径为rb、上平台相邻铰接点之间的夹角为α、基础平台相邻铰接点之间的夹角为β，平台高度为h(各支腿保持平衡时)，支腿的初始长度为l0，上平台质心相对于平衡位置的广义位移为

χp=[xpypzpαpβpγp]T

基础平台质心相对平衡位置的广义位移为

χb=[xbybzbαbβbγb]T

则上、下平台各铰接点在全局惯性坐标系中的坐标矢量为

(1)

(2)

上、下平台各铰接点在全局惯性坐标系中的速度矢量为

(3)

(4)

则各支腿的方向矢量为

忽略支腿特性且假设支腿对上平台的作用力仅仅体现在支腿方向上，则各个支腿对上平台的作用力分别为：

(5)

令f=[f1f2f3f4f5f6]T，则有

(6)

其中

对于质量惯性矩阵为M的上平台，由牛顿-欧拉方程可得

(7)

在支腿特性和载荷的质量惯性特性已经设定的情况下，惯性质量矩阵和刚度矩阵均为常矩阵；隔振平台的自由模态只和平台的参数尺寸和姿态有关。对于空间隔振平台，平台姿态变化是一个微小量，可以认为在振动过程中，其姿态不发生变化。因此隔振平台的自由模态仅仅和平台的参数尺寸有关。

设定各个支腿的特性相同，则当平台的广义刚度矩阵为

(8)

2 优化算法设计

优化算法设计主要包括根据待优化的性能指标确定目标函数模型，根据实际的各种限制确定约束函数模型，并根据目标函数模型和约束函数模型确定合适的优化算法。

2.1 目标函数模型

针对所要研究的问题，忽略空间隔振平台的阻尼项，则牛顿—欧拉动力学方程可简化为

(-ω2M+K)δ=f

(9)

式中:f为受到的力和力矩矢量;δ为线位移和角位移矢量。定义矢量

δ=[δxδyδzδθδψδφ]T
f=[TxTyTzFxFyFz]T

其中，Fx，Fy和Fz分别是沿X轴，Y轴和Z轴方向的主动力；Tx，Ty和Tz为主动力矩；δx，δy和δz分别为沿X轴，Y轴和Z轴方向的线性位移；δθ，δψ和δφ分别为绕X轴，Y轴和Z轴的旋转角位移。根据其单位的不同，可以划分为

力矢量F=[FxFyFz]T，
力矩矢量T=[TxTyTz]T，
线位移矢量δt=[δxδyδz]T
和角位移矢量δr=[δθδψδφ]T

进而刚度矩阵也可以根据单位的不同，划分为4个3×3的块矩阵，即：

(10)

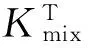
(11)

式中：m为载荷质量；Ix，Iy和Iz为轴转动惯量。(注：惯性质量矩阵的划分是基于载荷的质心和上平台中心完全重合，且载荷的惯性主轴和所定义的上平台坐标系完全重合的假设。)

引入动态刚度矩阵

Kdyn=Kdyn(ω)=-ω2M+K

(12)

(13)

K1=-ω2Mm+Ktr,K2=-ω2Sst+Kmix
K3=-ω2Sin+Krot

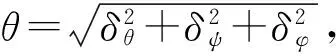
(14)

(15)

式中，cr和ct为螺旋轴的单位矢量，n为由于旋转角θ引起的沿坐标轴方向的平移位移且满足：

现已知螺距为pr，螺旋轴上位置矢量为r0的任一点，则螺旋量可以表示为

n=prcr+r0×cr

pr=ncr=nxcrx+nycry+nzcrz
r0=[cr×n]=[δr×δt]/θ2

(16)

则动力学共线刚度kdcs定义为单位旋量方向上的主动扭矩在相同旋量方向上产生的响应位移，即

kdcs(ω)=sTKdyn(ω)s

(17)

根据旋转角是否存在，则动力学共线刚度可表示为如下形式：

(18)

对于给定的平台结构，最小动力学共线刚度可表示为频率和结构尺寸的函数，即

则可以证明，如下关系成立

kt,min=λr,min=min[λt1,λt2,λt3]

其中λti为矩阵K1的特征根

kr,min=λr,min=min[λr1,λr2,λr3]

(19)

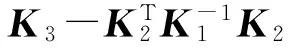
λti=-mω2+A(i,i)ki=1,2,3
λr3=-Izω2+A(6,6)k
λr1=-Ixω2+A(4,4)k+A(2,4)2k2/(-ω2m+A(2,2)k)
λr2=-Iyω2+A(5,5)k+A(1,5)2k2/(-ω2m+A(1,1)k)

由上述公式可知，在支腿特性一定的情况下，λti和λri的取值不仅取决于频率，而且和空间隔振平台的结构参数有关。定义空间隔振平台的结构参数设计矢量为X=[rbrpαβ]T，其中，rp和rb分别为上、下平台的平台半径；α和β分别为上、下平台相邻铰接点之间的夹角，则优化目标函数可表示为

2.2 约束函数模型

在空间隔振平台的设计过程中，往往是先进行支腿的设计。所以研究在支腿长度一定的情况下的空间隔振平台结构参数优化设计具有一定的工程实践意义。在支腿长度一定或支腿长度受限的情况下，各变量满足下面的约束关系：

(20)

由于空间隔振平台对工作空间的要求不高，参数的设计主要避免结构奇异。引入结构奇异性判别矩阵

(21)

对于空间隔振平台的应用要求，其最小动力学刚度需满足

kr,min(ω)≥(kr)lim且kt,min(ω)≥(kt)lim

其中(kr)lim,(kt)lim是在设计阶段选定的固定值。通常来说(kr)lim,(kt)lim的选取原则满足

(kr)lim=(0.2-0.4)(kr)ISO
(kt)lim=(0.2-0.4)(kt)ISO

(22)

(kt)ISO=2k

(23)

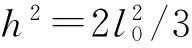
(24)

3 优化算法

鉴于待优化模型中设计变量与目标函数和约束条件之间的非线性关系，结合遗传算法在非线性优化方面的优良性能，这里采用遗传算法进行优化求解，有关参数选取如下

(1)适应度函数：由于遗传算法求解时适应度函数Fitness常取最大值，故取如下适应度函数：

(2)种群规模：M=100

(3)子代生成：设定交叉算子pc=0.85

选择算子采用随机一致选择算子；变异算子采用高斯变异算子。

(4)终止条件：适应度函数值较前一代函数值变化小于其0.01%，说明个体稳定在最优解，终止计算。

4 仿真算例

空间隔振平台的各项仿真时的约束条件及待优化变量的取值范围如表1所示。

将上述各参数及各变量的取值约束与适应度函数结合，经遗传算法寻优计算，得到如表2所示的变量参数。

优化得到的空间隔振平台的构型如图3所示。

表1 载荷和支腿参数及变量的取值范围

表2 各变量的优化值

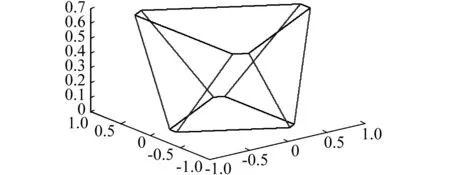
图3 优化后的空间隔振平台结构示意图Fig.3 The optimal structure for the vibration isolation platform

平台各个方向的共线动力学刚度随频率的变化曲线如图4所示(考虑到平台的结构对称性，只给出了Z轴和Y轴的平移和旋转方向)

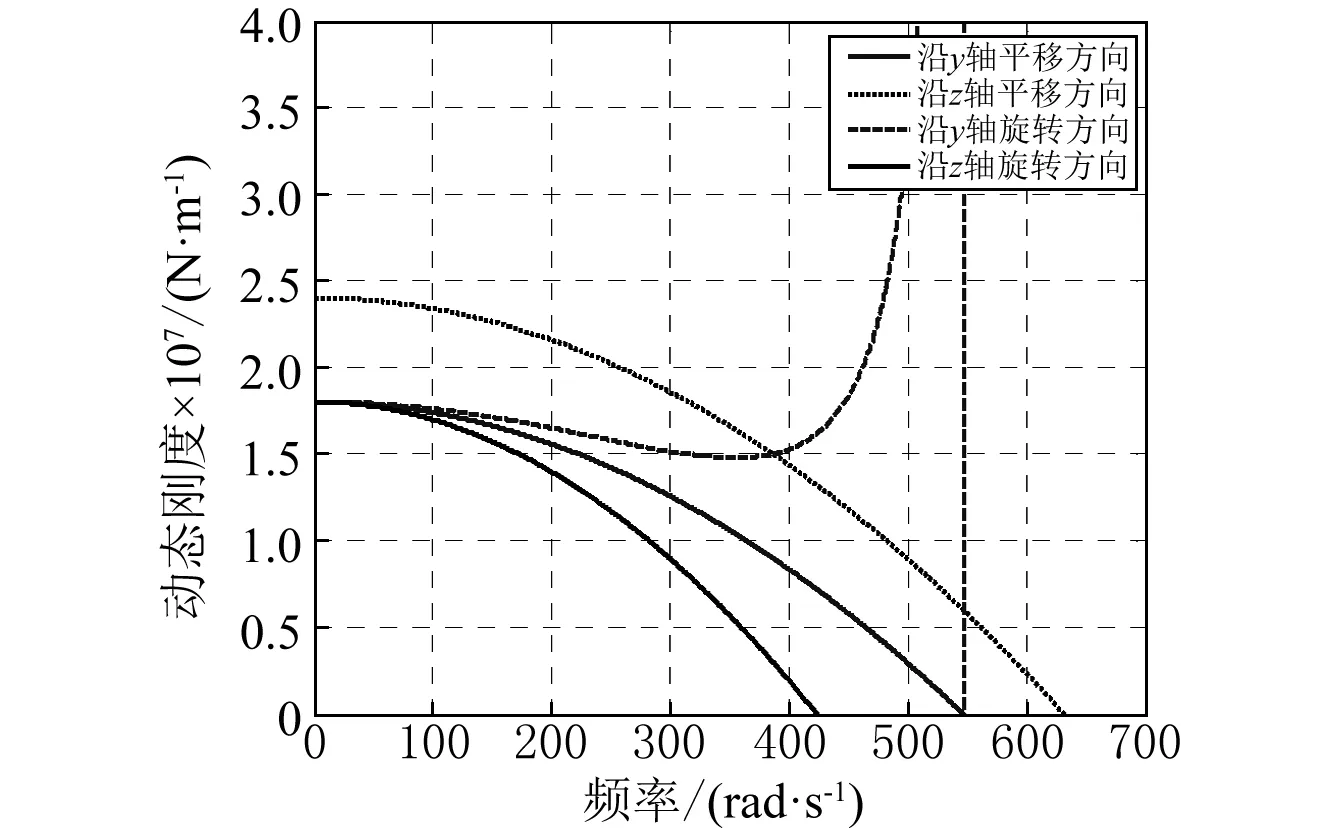
图4 空间隔振平台各方向的共线动力学刚度Fig.4 Dynamic collinear stiffness in different directions

由图4可知，经优化后的空间隔振平台最小静刚度为支腿刚度的1.8倍，在满足式(23)和式(24)要求的前提下，系统的带宽可以达到100 Hz，充分满足控制要求。对于Cubic结构的平台构型，其最小静刚度为单个支腿刚度的0.83倍，相对于优化结果，空间隔振平台的最小刚度值有显著提高。

5 结 论

研究了空间隔振平台结构参数：上、下平台半径，上、下平台与支腿相邻连接点之间的夹角与动力学共线刚度之间的关系。通过一个仿真算例，对空间隔振平台结构参数进行优化，并将优化结果与Cubic构型的空间隔振平台进行了比较，其指标明显优于Cubic构型的空间隔振平台。

[1] STEWART D. A platform with six degrees of freedom[J]. Proceedings of the Institution of Mechanical Engineers, 1965/1966, 180: 1-15.

[2] RAO KOTESWARA A B, RAO P V M, SAHA S K. Dimensional design of hexaslides for optimal workspace and dexterity[J]. IEEE Transactions on Robotics, 2005, 21(3):444-449.

[3] GOSSELIN C M, ANGELES J. A global performance index for the kinematic optimization of robotic manipulators[J]. ASME Journal of Mechanical Design, 1991,113(3):220-226.

[4] MANSOURI I, OUALI M. The power manipulability a new homogeneous performance index of robot manipulators[J]. Robotics and Computer Integrated Manufacturing, 2011, 27(2):434-439.

[5] HONG K S, KIM J G. Manipulability analysis of a parallel machine tool:application to optimal link length design[J]. Journal of Robotic Systems, 2000, 17(8):403-415.

[6] LECOURS A, GOSSELIN C M. Reactionless two-degree-of-freedom planar parallel mechanism with variable payload[J]. ASME Journal of Mechanisms and Robotics, 2010, 2(4):041010-1-7.

[7] ILIA D, SINATRA R. A novel formulation of the dynamic balancing of five-bar linkages with applications to link optimization[J]. Multibody System Dynamics, 2009, 21(2):193-211.

[8] MA O, ANGELES J. Optimum design of manipulators under dynamic isotropy conditions[C]// Proceedings of the IEEE international conference on robotics and automation. Atlanta, USA, 1993: 470-475.

[9] TONG Z Z, HE J F, JIANG H Z, et al. Optimal design of a class of generalized symmetric Gough-Stewart parallel manipulators with dynamic isotropy and singlarity-free workspace[J]. Robotica, 2012, 30(2):305-314.

[10] LI H H, YANG Z Y, HUANG T. Dynamics and elasto-dynamics optimization of a 2-DOF planar parallel pick-and-place robot with flexible links[J]. Structural and Multidisciplinary Optimization, 2009, 38(2):195-204.

[11] SILVA M M D, OLIVEIRA L P R D, BRÜLS O, et al. Integrating structural and input design of a 2-DOF high-speed parallel manipulator: a flexible model-based approach[J]. Mechanism and Machine Theory, 2010, 45(11):1509-1519.

[12] XU Q S, LI Y M. Error analysis and optimal design of a class of translational parallel kinematic machine using particle swarm optimization[J]. Robotica, 2009, 27(1):67-78.

[13] CHI Z Z, ZHANG D. Stiffness optimization of a novel reconfigurable parallel kinematic manipulator[J]. Robotica, 2012, 30(3):433-447.

[14] 夏禹，黄海. Hexapod 平台参数设计优化[J]. 航空学报，2008，29(5):1168-1173.

XIA Yu,HUANG Hai. Design optimization for hexapod platform parameters[J]. Acta Aeronautica et Astronau Tica Sinica, 2008, 29(5):1168-1173.

[15] PORTMAN V T, CHAPSKY V S, SHNEOR Y. Evaluation and optimization of dynamic stiffness values of the PKMS: Colinear stiffness value approach[J]. Mechanism and Mechine Theory, 2014, 74(6):216-244.

Structure optimization for a space-based vibration isolation platform based on dynamic collinear stiffness

ZHANG Yongliang1, GUO Baiwei2

(1.The Third Research Institute of China Electronics Technology Group Corporation, Beijing 100015, China;2.Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

A new performance appraisal index, dynamic collinear stiffness, was introduced to deal with the optimizing design about structure parameters of a space-based vibration isolation platform. The radii of the top and bottom platforms and the central angle corresponding to the adjacent connection points were taken as the design variables, the maximization of the minimum of the dynamic collinear stiffness was taken as the objective function and the engineering design requirements with respect to the dynamic stiffness within a specified frequency range were taken as the constraints. A mathematical model was built based on the design variables, the objective function and the constraints and the optimal solution was gotten by the GA tools. The simulation shows that the optimal solution meets the engineering design requirements and the performance appraisal index is better than the conventional ones.

vibration isolation platform; dynamic collinear stiffness; genetic algorithm(GA); optimization

北京理工大学基础研究基金项目(20130142015)

2015-12-30 修改稿收到日期： 2016-05-25

张永亮 男，博士生，1984年生

郭百巍 男，博士，副教授，1976年生

TH113

A

10.13465/j.cnki.jvs.2017.14.018