推进轴系参数优化对水下结构声振特性影响研究

李海峰， 何其伟， 俞 翔， 朱石坚

(1.海军工程大学 动力工程学院,武汉 430033; 2.船舶振动噪声重点实验室,武汉 430033)

推进轴系参数优化对水下结构声振特性影响研究

李海峰1,2， 何其伟1,2， 俞 翔1,2， 朱石坚1,2

(1.海军工程大学 动力工程学院,武汉 430033; 2.船舶振动噪声重点实验室,武汉 430033)

在修正Timoshenko梁基础上，采用传递矩阵法推导了水下结构推进轴系简化模型的传递矩阵，实现各轴承位置处振动功率流的求解。以各轴承位置处传递功率流作为优化目标，选择三组不同的优化方案，取艉轴前后轴承刚度、推力轴承刚度以及轴承间距为优化变量对推进轴系参数进行优化。利用三维水弹性力学理论和三维水弹性声学分析软件，计算分析不同优化结果下水下结构的声源级曲线。结果表明：以艉轴后轴承、艉轴前轴承和推力轴承各处传递功率流最小为优化目标的优化方案最有利于减小水下结构的声辐射。

推进轴系；传递矩阵法；功率流；参数优化；声源级

螺旋桨不均匀动载荷引起的推进轴系振动是水下结构的主要机械噪声源，严重影响其声隐身性能[1]。因此，研究推进轴系参数的合理优化设计对于提高其作战性能具有重要的意义。

之前，Feng等[2]研究了轴承刚度对推进轴系振动传递特性的影响。周春良[3]研究了轴承间距对船舶推进轴系振动特性的影响。杨志荣等[4]研究了推进轴系的纵向振动并提出了有效的控制措施。但上述研究工作仅单纯分析了推进轴系的振动，并没有分析推进轴系对水下结构振动声辐射的影响。针对这一问题，曹贻鹏等[5-6]研究了轴系-壳体耦合系统的振动声辐射问题，Merz等[7-8]研究了桨-轴-壳体模型在螺旋桨激励力下的振动声辐射，但并未综合考虑推进轴系参数的多变量多目标优化问题对水下结构振动声辐射的影响。对于复杂水下结构的振动声辐射问题，解析法求解很难实现。Wu等[9]将三维适航理论与结构力学理论相结合，在考虑水为不可压缩介质的情况下，提出了三维水弹性力学理论。Zou等[10]等在三维水弹性力学理论基础上研究了水下弹性体结构近场点声压和远场声辐射的计算方法，同时对计算方法的有效性进行了验证，并在Abaqus软件的基础上二次开发了三维水弹性声学分析软件Thafts-acoustic，利用该方法和软件能够实现潜艇等复杂结构的振动和声辐射计算[11]。

本文参照基本的潜艇结构建立了三维桨-轴-壳体简化模型，采用传递矩阵法，将轴系简化为梁单元、质量点单元和弹性支承单元，从修正的Timoshenko梁理论出发，求出梁段左右两侧状态矢量之间的关系式，得到梁的场矩阵表达式；结合螺旋桨质量点处和轴承弹性支承处的点矩阵表达式，组成推进轴系的整个振动传递矩阵，实现各轴承位置处振动功率流的求解；然后，分别以各轴承位置处传递功率流作为优化目标，取艉轴前后轴承刚度、推力轴承刚度以及轴承间距为优化变量对推进轴系参数进行优化；最后，利用三维水弹性力学理论和三维水弹性声学分析软件，计算分析不同优化结果下壳体结构的声源级曲线，研究其对水下结构振动与声辐射特性的影响。

1 计算模型及原理

文中将基本的潜艇结构简化为桨-轴-壳体模型，如图1所示，简化模型中包括壳体结构、艉轴、螺旋桨、艉轴后轴承、艉轴前轴承和推力轴承。由于推力轴承纵向刚度对水下结构横向振动影响较小，所以，模型中轴承均简化为水平和垂直方向刚度的弹簧，桨-轴-壳体结构参数如表1所示。

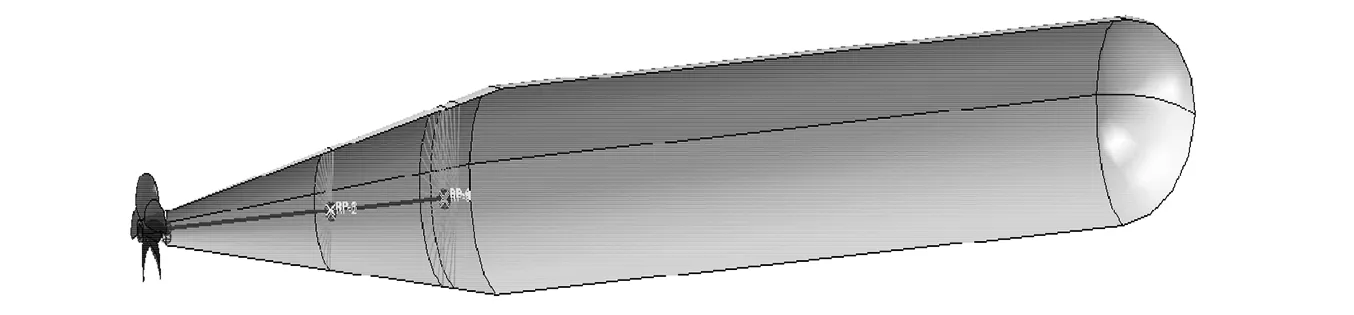
图1 桨-轴-壳体简化模型Fig.1 Simplified model of the propeller-shaft-hull coupled structure

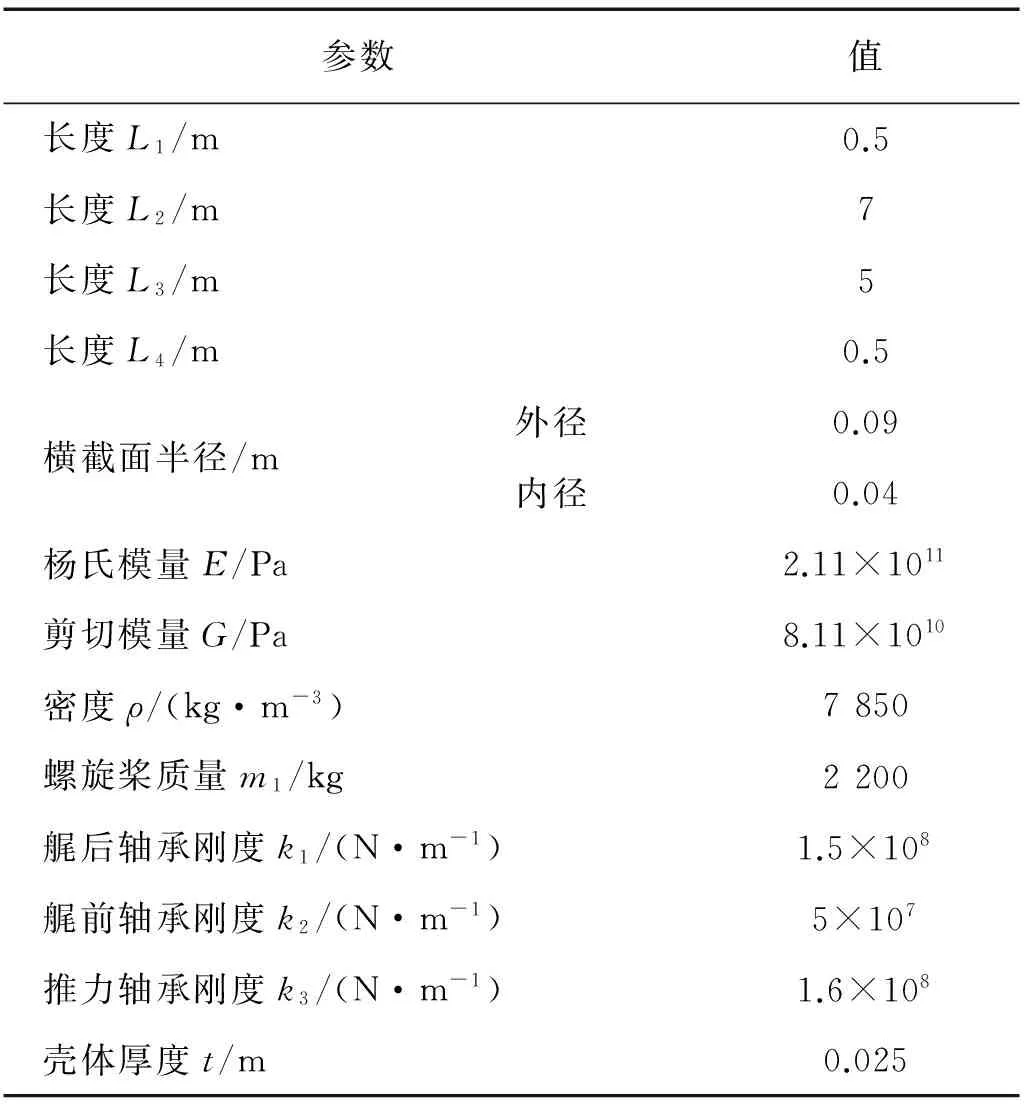
参数值长度L1/m0.5长度L2/m7长度L3/m5长度L4/m0.5横截面半径/m外径0.09内径0.04杨氏模量E/Pa2.11×1011剪切模量G/Pa8.11×1010密度ρ/(kg·m-3)7850螺旋桨质量m1/kg2200艉后轴承刚度k1/(N·m-1)1.5×108艉前轴承刚度k2/(N·m-1)5×107推力轴承刚度k3/(N·m-1)1.6×108壳体厚度t/m0.025

1.1 船舶推进轴系的传递矩阵计算

把图1中的轴系划分为4个单元，相应节点编号为0,1,2,3,4，螺旋桨简化为质量点单元，轴承简化为弹性支承单元，如图2所示。推进轴系质量分布均匀，横截面为空心圆形，抗弯刚度为EI，单位长度的质量为m，截面面积为A。

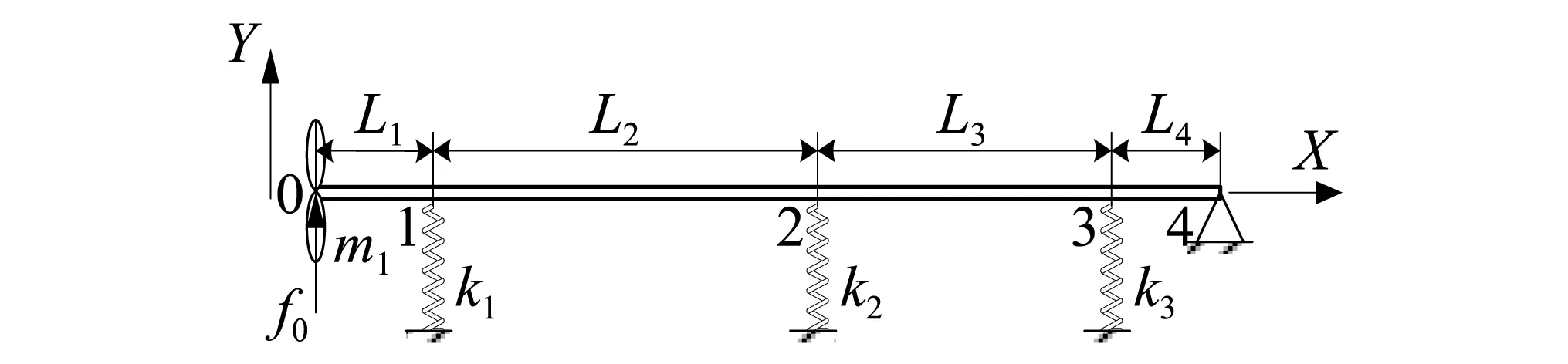
图2 推进轴系结构简化模型Fig.2 Simplified model of propulsion shafting structure

(1)

[T]为轴系两端状态矢量的场传递矩阵，其为4×4的方阵，并且有

T=U4T4U3T3U2T2U1T1U0

(2)

式中：Ui(i=0,…,4)为各节点矩阵；Tj(j=0,…，4)为各段梁单元场矩阵。

求解梁单元的场传递矩阵，一般采用Timoshenko梁理论，虽然Timoshenko梁理论比Bernoulli-Euler梁理论更精确，但其也忽略了由剪切变形引起的转动惯量对梁弯曲振动的影响。陈镕等[12]在Timoshenko梁理论的基础上，对Timoshenko梁的弯曲振动方程进行了修正，同时考虑由剪切变形引起的转动惯量对梁弯曲振动的影响。

根据修正Timoshenko梁的自由弯曲振动方程

(3)

式中：k′为剖面有效剪切系数。

由式(3)可以得到第i段梁单元的场传递矩阵为

(4)

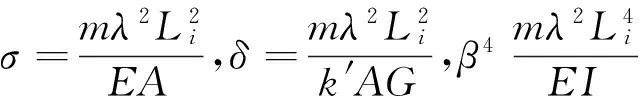
C5=s1shs1+s2sins2，C6=s1sins2-s2shs1，

根据第i段和第i+1(i=1,…,3)段单元连接节点 处力的平衡和位移协调条件，可以得到集中质量点和弹簧支撑处的点矩阵分别为：

图2所示的推进轴系两端的边界条件分别为：

最左端为自由端：剪力和弯矩等于零，

M0=Q0=0

(5)

最右端为简支端：位移和弯矩等于零，

y4=M4=0

(6)

将式(5)和式(6)代入式(1)中，可得到

(7)

求解式(7)可以得到轴系最左端的状态矢量为

(8)

将式(8)代入式(1)中，并根据不同轴段单元间的传递矩阵，即可求得各轴承支撑位置处的位移响应和内力。

对于频率为w的简谐运动，稳态功率流定义为一个周期内的能量平均值

(9)

式中：Re()表示取实部；上标“*”表示取共轭；U(w)和V(w)为广义位移向量和广义速度向量。

从而，可以得到图2中推进轴系通过第i个(i=1,…,3)路径传递到轴承基础上的功率流为

(10)

Fi(w)，Vi(w)分别为推进轴系通过第i个(i=1,…,3)路径传递到轴承基础上的力和基础上第i个(i=1,…,3)路径的速度响应。

1.2 三维声弹性力学理论

由模态叠加法，船体结构离散系统的节点位移可表示为

(11)

式中：qr(r=1,2,…,m)为第r阶干模态的主坐标分量。

假设弹性船体周围水为均匀可压，无黏的理想声介质，只考虑船舶航行诱导的扰动流场以及由结构振动诱导的声波场都是微幅线性的，总的流场速度势可表示为各阶声波辐射速度势的线性叠加

(12)

式中：(x,y,z)为场点的坐标。

声波速度势φ满足Helmholtz方程为

(13)

船体流固湿表面边界条件为

(14)

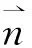
与自由液面边界条件对应的Green函数为

(15)

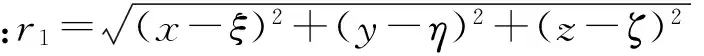
针对各阶干模态可得到对应的简单源边界积分方程

(16)

频域内的船舶声弹耦合动力学方程为

(17)

式中：{q}为广义位移向量；{Ξ}为广义力向量；[a]，[b]，[c]为干结构广义质量、阻尼和刚度矩阵；[A]，[B]，[C]为广义流体附加质量、附加阻尼和恢复力系数矩阵，其表达式为

(18)

(19)

流场中辐射波声压为

(20)

2 数值计算及结果分析

2.1 推进轴系的参数优化

推进轴系的参数优化模型可以表示成多个目标优化的一般形式

(21)

式中：F(X)=min(f1(X),f2(X),…,fp(X))T称为向量目标函数，其表达的含义是：在不等式约束条件gi(X)≤0和等式约束条件hi(X)=0下，求解设计变量X=(x1,x2,…,xn)T，使F(X)中各目标函数被同等地极小化。

2.1.1 优化变量

由于推力轴承和艉轴后轴承安装位置改变比较困难，而改变艉轴前轴承的布置位置是可以实现的。因此，保持推力轴承和艉轴后轴承的位置不变，选取艉轴后轴承刚度k1，艉轴前轴承刚度k2、推力轴承刚度k3以及艉轴前轴承与推力轴承的间距L2为优化变量，即

X=(k1,k2,k3,L2)

(22)

优化变量的取值范围如表2所示。

表2 优化变量的取值范围

2.1.2 优化目标

为对比不同优化目标的优化效果，文中选择三组不同的优化方案进行优化，即，

优化方案一

考虑到横向激励下，艉轴后轴承是主要的传递路径，因此，选取推进轴系在0～150 Hz频段内艉轴后轴承处传递功率流最小为优化目标函数，此为单目标优化问题

min(F(X))=min(f1(x)=∑P1i)

(23)

优化方案二

选取推进轴系在0～150Hz频段内艉轴后轴承、艉轴前轴承和推力轴承三处传递功率流之和最小为优化目标函数，此为单目标优化问题

min(F(X))=min(f1(x)+f2(x)+f3(x))=
min(∑P1i+∑P2i+∑P3i)

(24)

优化方案三

选取推进轴系在0～150Hz频段内艉轴后轴承、艉轴前轴承和推力轴承各处传递功率流最小为优化目标函数，此为多目标优化问题

min(F(X))=min(f1(x),f2(x),f3(x))

(25)

式中，P1i、P2i、P3i分别表示艉轴后轴承、艉轴前轴承和推力轴承处的传递功率流。

2.1.3 约束函数

因为推力轴承和艉轴后轴承位置不变，因此定义等式约束条件为

L2+L3=12

(26)

2.1.4 优化计算

文中选用Isight提供的Pointer优化器对推进轴系进行单目标优化；选用NSGA-Ⅱ优化算法进行多目标优化，种群规模为12，最大遗传进化代数为20，交叉概率选定0.9，经过优化计算一共得到87个Pareto解，并给出一组最优解，Pareto解集的三维分布情况如图3所示。优化结果如表3所示。

图3 Pareto解集Fig.3 The set of Pareto solution

序号k1k2k3L2f1(X)f2(X)f3(X)优化17.5×1081.8×1086.18×1074.0813789398639优化24.6×1071.4×1088.0×1087.1964865094374优化35.0×1071.2×1087.3×1084.8963867704464

2.2 参数优化对结构声振特性的影响

为对比分析三种不同优化方案的优化效果，本文在Abaqus中建立了桨-轴-壳体有限元模型以及壳体结构与流体接触的湿表面，如图4所示。螺旋桨为5叶三维桨，采用3D实体单元模拟；壳体和轴系分别采用2D壳单元和1D梁单元模拟，轴承采用弹簧单元模拟，其刚度和间距按不同的优化结果分别设置。在螺旋桨桨毂的中心位置施加幅值为1 N的垂向激励力，在5～150 Hz频率范围内用三维声弹性响应计算软件，计算水下壳体结构在无限水深介质中产生的辐射声功率，按式(27)换算为声源级。

(27)

式中，P为辐射声功率量值，基准值P0=0.65×10-18W/Hz。

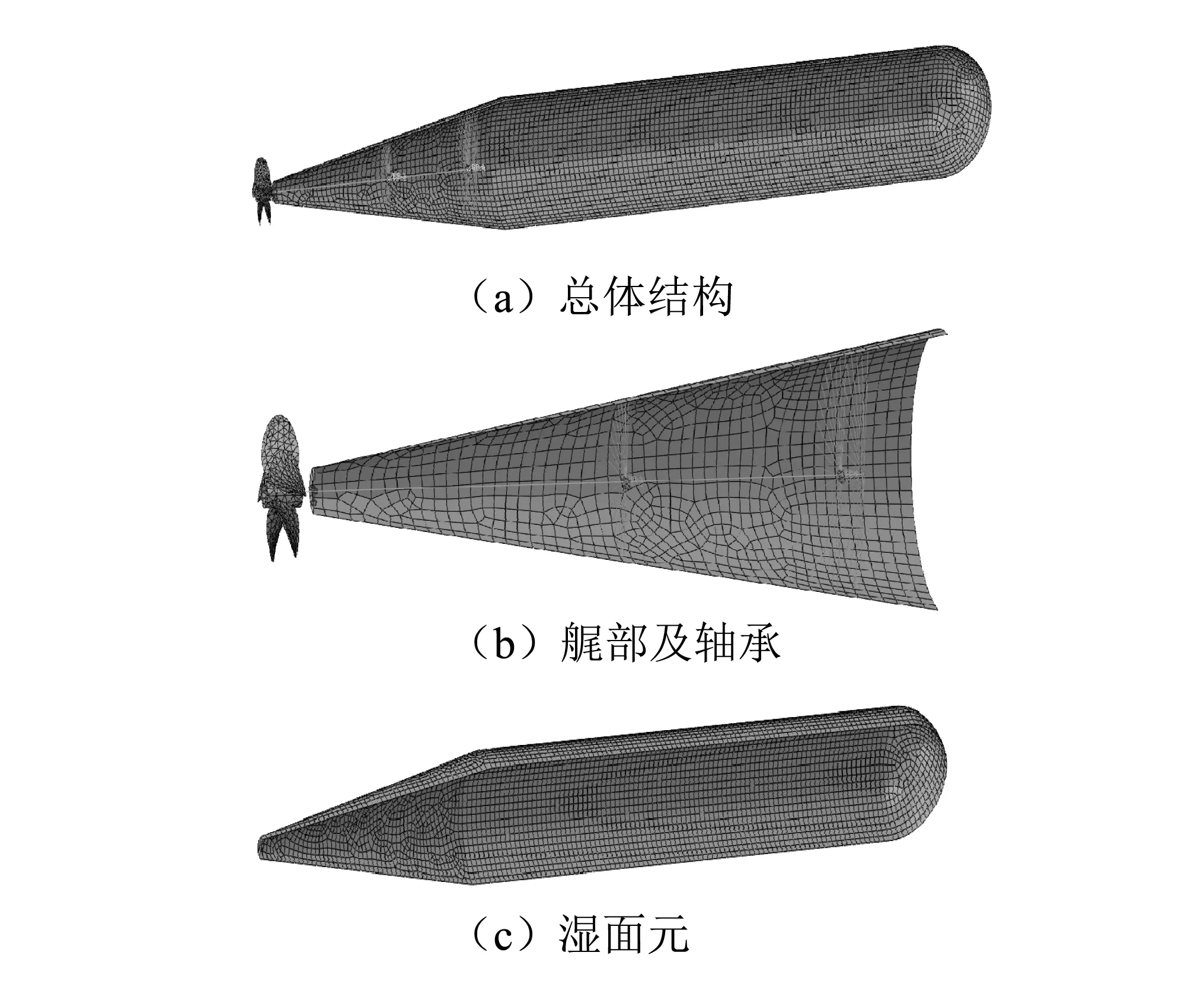
图4 桨-轴-壳体有限元模型Fig.4 FE model of the propeller-shaft-hull coupled structure

在不同的优化方案下，计算得到桨-轴-壳体结构的声辐射声源级曲线，并与优化前的原始方案进行对比，如图5所示。从图中可以看出，仅以艉轴后轴承处传递功率流最小为优化目标的优化方案一并没有取得良好的减振降噪效果，该优化方案反而增加了水下结构在5～150 Hz频段内的声辐射，计算得到优化前水下结构在5～150 Hz频段内声辐射总声级为103.1 dB，优化方案一后水下结构在5～150 Hz频段内总声级为104.8 dB，因此，这种优化方案是不可取的。优化方案二和优化方案三均取得了较明显的减振降噪效果，优化方案二后水下结构在5～150 Hz频段内总声级为101.4 dB，优化方案三后水下结构在5～150 Hz频段内总声级为99.0 dB，优化方案三的效果更优于优化方案二，而且在40 Hz以下的频段内，水下结构的声源级曲线峰值频率产生了变化，这主要是由于不同的优化方案下得到不同的优化参数，改变了推进轴系前几阶弯曲振动的振动状态，所以，在设计阶段，应综合考虑合理的优化方案以避免推进轴系模态与艇体某阶振动模态接近而产生明显的共振现象。

图5 水下结构声辐射声源级曲线Fig.5 The sound source level curve of the underwater structure

3 结 论

文中采用传递矩阵法，在修正Timoshenko梁基础上，推导了水下结构推进轴系简化模型的传递矩阵，实现各轴承位置处振动功率流的求解。然后，以各轴承位置处传递功率流作为优化目标，选择艉轴后轴承处功率流最小为优化方案一；艉轴后轴承、艉轴前轴承和推力轴承三处传递功率流之和最小为优化方案二；艉轴后轴承、艉轴前轴承和推力轴承各处传递功率流最小为优化方案三，取艉轴前后轴承刚度、推力轴承刚度以及轴承间距为优化变量对推进轴系参数进行优化。最后，利用三维水弹性力学理论和三维水弹性声学分析软件，计算分析不同优化结果下水下结构的声源级曲线，结果表明优化方案三能取得最好的减振降噪效果，优化方案二次之，优化方案一无法取得较好的效果。文中的研究结果对于船舶推进轴系的结构设计具有较好的指导意义。

[1] 施引，朱石坚，何琳. 船舶动力机械噪声及其控制[M]. 北京：国防工业出本社，1990.

[2] FENG G P, ZHANG Z Y, CHEN Y. Research on transmission paths of a coupled beam-cylindrical shell system by power flow analysis [J]. Journal of Mechanical Science and Technology，2009，23：2138-2148.

[3] 周春良.船舶轴系振动研究[D].哈尔滨：哈尔滨工程大学动力与能源学院，2006.

[4] 杨志荣，秦春云，饶柱石.船舶推进轴系纵振动力吸振器设计及参数影响规律研究[J].振动与冲击，2007,26(8):101-103. YANG Zhirong, QIN Chunyun, RAO Zhushi. Design and analysis of a dynamic absorber for reducing axial vibration of ship shafting [J]. Journal of Vibration and Shock, 2007,26(8):101-103.

[5] 曹贻鹏.推进轴系引起的艇体结构振动与辐射噪声控制研究[D].哈尔滨：哈尔滨工程大学动力与能源学院，2008.

[6] 李栋梁.轴系-艇体耦合系统振动声辐射分析与实验研究[D].上海：上海交通大学，2012.

[7] MERZ S，KINNS R，KESSISSOGLOU N. Structural and acoustic responses of a submarine hull due to propeller forces[J]. Journal of Sound and Vibration, 2009,325:266-286.

[8] WEI Y S，WANG Y S, DING K. Submarine underwater structure-borne noise and flow noise due to propeller excitation[J]. Acoustics Australia,2012,40(2):122-127.

[9] WU Y S. Hydroelasticity of floating bodies[D].London: Brunel University,1984.

[10] ZOU M S, WU Y S, YE Y L. Three-dimensional hydroelasticity analysis of acoustic responses of ship structures[C]∥9th International Conference on Hydrodynamics. Shanghai, 2010, 10:844-851.

[11] 祁立波，邹明松.加肋圆柱体水下低频辐射声特性研究[J].船舶力学，2015,19(7): 874-883. QI Libo, ZOU Mingsong. Research on acoustic radiation of stiffened cylinder in low-frequency [J]. Journal of Ship Mechanics, 2015,19(7): 874-883.

[12] 陈镕,万春风，薛松涛,等.Timoshenko梁运动方程的修正及其影响[J].同济大学学报(自然科学版),2005, 33(6):711-715. CHEN Rong, WAN Chunfeng, XUE Songtao. Modification of motion equation of Timoshenko beam and its effect[J].Journal of TongJi University(Natural Science),2005, 33(6):711-715.

Effects of propulsion shafting parameters optimization on the vibra-acoustic radiation of underwater structures

LI Haifeng1,2, HE Qiwei1,2, YU Xiang1,2, ZHU Shijian1,2

(1. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China；2. National Key Laboratory on Ship Vibration & Noise, Wuhan 430033, China)

The expression of field transfer matrix of a ship propulsion shafting was deduced based on the modified Timoshenko beam theory and the transfer matrix method. The power flow at each bearing of the propulsion shafting was solved numerically. The propulsion shafting parameters were optimized with three different optimization schemes by selecting the aft stern shaft bearing stiffness , front stern shaft bearing stiffness, thrust bearing stiffness and bearing spacing length as optimization design variables and selecting the sum of the power flows at each bearing of the propulsion shafting as an optimization objective. The three-dimensional sono-elastical theory and acoustic analysis software were applied to analyze the sound source level curve of the underwater structure in the light of the optimization results of different schemes. The analysis results show that the acoustic radiation of the underwater structure is smallest when adopting the optimization scheme that the power flow at each bearing of the propulsion shafting is minimal.

propulsion shafting; transfer matrix method; power flow; parameters optimization; sound source level

国家自然科学基金资助项目(51579242);国家自然科学基金青年基金资助项目(51509253)

2016-04-08 修改稿收到日期： 2016-06-14

李海峰 男，博士生，1988年生

何其伟 男，副教授，1972年生

TB533

A

10.13465/j.cnki.jvs.2017.14.015