箱体柔性对齿轮传动系统动态特性的影响分析

任亚峰， 常 山， 刘 更， 吴立言

(1. 西北工业大学 陕西省机电传动与控制工程实验室，西安 710072；2. 703研究所，哈尔滨 150036)

箱体柔性对齿轮传动系统动态特性的影响分析

任亚峰1， 常 山2， 刘 更1， 吴立言1

(1. 西北工业大学 陕西省机电传动与控制工程实验室，西安 710072；2. 703研究所，哈尔滨 150036)

分别建立了齿轮、轴、轴承及箱体的阻抗模型，并采用阻抗综合法建立了“齿轮-轴-轴承-箱体”耦合动力学模型，实现了传动系统与箱体的耦合。以单级斜齿轮减速器为对象，计算了“齿轮-轴-轴承-箱体”耦合系统的固有频率，以及耦合系统在轮齿时变啮合刚度激励下的齿轮动态啮合力及轴承动态支反力，并与不耦合箱体的情况进行了对比。结果表明：耦合箱体后，系统的固有频率降低了；箱体柔性对轴承动态支反力的影响要大于对齿轮动态啮合力的影响；考虑箱体柔性后，系统的振动可能减小，也可能加剧，取决于系统的工作转速。

齿轮动力学；箱体柔性；耦合振动；阻抗综合

由于齿轮时变啮合刚度、加工误差及安装误差的存在，传动系统不可避免地会产生振动。这种振动经传动轴传递到轴承，进而传递到箱体，引起箱体振动并辐射噪声。应用最广泛的齿轮系统动力学模型为集中质量模型[1]，该模型可以计算轴承支反力。通过建立箱体有限元/边界元模型并施加轴承激振力边界条件即可得到箱体结构噪声及空气噪声[2]。但在现有的齿轮传动系统集中质量模型大都没有考虑箱体的影响。Abbes等[3]采用子结构模态综合法，通过各个子结构的固有频率及振型得到了整个系统的固有频率及振型。Hambric等[4]认为轴承与箱体通过影响轴的边界条件来影响齿轮振动。 Rigaud等[5]用有限元法研究了耦合箱体对传动系统的影响，认为耦合箱体后对齿轮动态啮合力有显著影响的模态个数会增加。Choy等[6]采用模态坐标缩减了系统的自由度并获得了耦合箱体后多级齿轮传动系统的瞬态响应，认为箱体对刚性转子的影响更大。林腾蛟等[7]建立了传动系统与箱体的耦合有限元模型，并采用模态叠加法对系统动响应进行了分析。Zhu等[8]采用静态子结构法研究了考虑箱体后的齿轮动态啮合力，但是由于静态子结构法忽略了箱体的惯性力，因此只能适用于低频计算。贺朝霞等[9]认为箱体吸收并传递了部分能量，导致行星传动系统的齿轮啮合力与轴承支反力均有较大程度的降低。Liu等[10]采用ADAMS建立了传动系统-箱体刚柔混合模型，研究表明箱体对齿轮啮合力影响很小但是会加剧轴承的振动。Yi等[11]同时建立了全有限元模型及集中质量模型，认为箱体对齿轮的影响很小，而对轴承载荷波动及辐射噪声有很大的影响。高维金等[12]采用 Craig-Bampton 动力缩减法考虑箱体的柔性，认为对于扭矩波动带来的振动能量在高频段以后经过齿轮-轴-轴承就已经衰减了。

现有的研究大都需要建立箱体的实体模型，并不能直接利用试验数据。为了实现理论模型与试验数据的结合，本文采用谐响应分析来模拟试验获得箱体阻抗，并采用阻抗综合法实现箱体与传动系统的耦合。

1 子系统阻抗综合法

一个稳定的线性振动系统，在简谐交变力f(t)作用下所产生的稳态响应x(t)，必定也是同频率的谐振动。稳定的、定常的、线性振动系统的机械阻抗，即等于简谐激励与其所引起的稳态响应的复数比。

(1)

式中：Z为机械阻抗；F为系统激振力；X为系统稳态响应(位移、速度和加速度)。

机械阻抗的倒数即为机械导纳，也称为频率响应函数，可表示为

(2)

由于系统的响应可以是位移、速度和加速度，因此机械阻抗和导纳亦有三种不同形式：位移、速度及加速度阻抗和导纳。通常所指的阻抗(导纳)为速度阻抗(导纳)，本文采用位移阻抗(导纳)，又称为动刚度(动柔度)。

阻抗综合法是分析组合结构系统动力特性的一种有效手段。图1以两个自由度耦合的组合系统为例进行说明。

图1 阻抗综合原理Fig.1 Impedance synthesis scheme

A、B两个子系统的阻抗方程可表示为

(3)

(4)

式中：Z为机械阻抗；上标A(B)表示子系统A(B)；下标i(i=1,2,3)为节点i；X为系统响应；F为系统激励。

位移协调方程为

(5)

力平衡方程为

(6)

联立式(3)～(6)可得组合系统的动力学方程

(7)

与静刚度矩阵叠加原理相同，总体结构系统的阻抗矩阵就等于所有子结构的阻抗矩阵按节点组装的结果。

2 “齿轮-轴-轴承-箱体”耦合阻抗建模

典型的齿轮减速器通常包括齿轮、轴、轴承以及箱体等，然而通常的齿轮系统动力学模型中并没有考虑箱体。本文所研究的减速器模型如图2所示，包括传动系统与箱体两部分。传动系统为滚动轴承支撑的单级斜齿轮传动，输入转速为1 080 r/min，负载扭矩为300 N·m。箱体的基本尺寸为410 mm×330 mm×215 mm，壁厚及肋板厚度均为6 mm。

图2 减速器模型Fig 2. The gearbox model

齿轮基本参数见表1。

表1 齿轮基本参数

2.1 子系统阻抗建模

2.1.1 齿轮副子系统阻抗建模

将齿轮副简化为质量弹簧系统，如图3所示。令齿轮副的广义位移为Xm={xp,yp,zp,θxp,θyp,θzp,xg,yg,zg,θxg,θyg,θzg}，则轮副沿啮合线方向的相对位移δ可由式(8)进行计算。

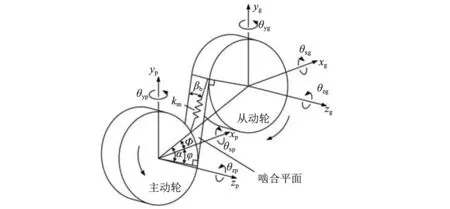
图3 齿轮动力学模型Fig 3. Gear dynamic model

(8)

式中，VP为投影向量，可由式(9)计算。

VP=[cosβbsinφ,±cosβb,sinβb, ∓rPsinβbsinφ,-rpsinβbcosφ,±rpcosβb-cosβbsinφ,∓cosβbcosφ,-sinβb, ∓rgsinβbsinφ,-rgsinβbcosφ,±rgcosβb]

(9)

式中，rp为小齿轮基圆半径，rg为大齿轮基圆半径，φ=α∓φ为端面啮合线与y轴的夹角，α为啮合角，φ为安装相位角，符号±与∓的上半部分用于小齿轮逆时针旋转，下半部分用于小齿轮顺时针旋转的情况。

根据牛顿第二定律可以列出啮合副单元的动力学方程，如式(10)所示。

(10)

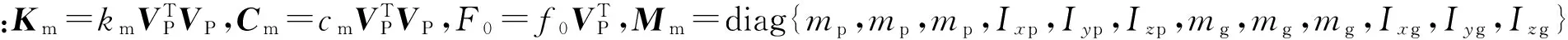
去掉式(10)左边的惯性项和阻尼项，可得啮合副单元的准静态动力学方程

Km(t)XS(t)=F0

(11)

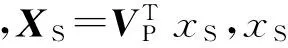
将方程中的时变项分解为均值和波动部分

XS(t)=X0+ΔXS

(12)

X(t)=X0+ΔX

(13)

K(t)=X0+ΔK

(14)

联立式(10)～(14)，可得式(15)

K0ΔXS(t)+ΔK[ΔXS(t)-ΔX(t)]

(15)

由于式(15)中ΔX为未知项，在方程右端以ΔXS近似ΔX，可以得到式(16)。啮合刚度和静态传递误差的计算参考文献[13]。

(16)

由于激振力和振动位移是以齿频为周期的函数，因此可以展成傅里叶级数的形式。式(16)可转为频域形式。

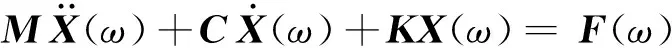
(17)

令ZGP(ω)=-ω2M+jωC+K，则得到啮合副单元的阻抗方程

(18)

式中ZGP为啮合副单元的阻抗矩阵，XGP为位移列向量，FGP为激振力列向量。

2.1.2 轴子系统阻抗建模

对于轴子系统，采用轴段有限元法进行建模，如图4所示。针对每一轴段，建立2节点12自由度的Timoshenko梁单元。

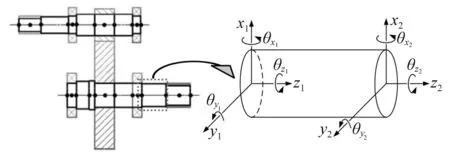
图4 轴子系统动力学模型Fig 4. Shaft sub-system dynamic model

令轴段单元的广义位移为Xsh= {x1,y1,z1,θx1,θy1,θz1,x2,y2,z2,θx2,θy2,θz2}。轴段单元的刚度矩阵如式(19)所示。

(19)

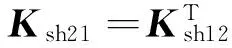
式中，E为材料弹性模量，G为材料剪切弹性模型，A为单元的横截面面积，l为单元的长度，Ix为在yz坐标平面内的截面惯性矩，Iy为在xz坐标平面内的截面惯性矩，J为极惯性矩，k为考虑实际剪切应变和剪切应力不是均匀分布而引入的校正因子，对于圆形截面可取k=10/9。

轴段单元的质量矩阵如式(20)所示。

(20)

Msh21=Msh12
Msh22=Msh11

式中，ρ为材料密度。

阻尼采用Rayleigh阻尼

Csh=α0Msh+α1Ksh

(21)

式中：α0为质量系数；α1为刚度系数。

轴段单元的动力学方程可表示为式(22)

(22)

轴段单元的阻抗矩阵可表示为式(23)。

[Zsh]{Xsh}={Fsh}

(23)

式中：Zsh为轴段单元的阻抗矩阵；Xsh为位移列向量;Fsh为激振力列向量。

2.1.3 轴承子系统阻抗建模

轴承采用弹簧阻尼单元描述，包含两个节点。刚度矩阵表示为式(24)。

(24)

(25)

阻尼采用Rayleigh阻尼

CBr=α1KBr

(26)

式中，α1为刚度系数。

轴承单元的阻抗方程可表示为式(27)

[ZBr]{XBr}={FBr}

(27)

式中：ZBr为阻抗矩阵；ZBr=jωCBr+KBr，XBr为位移列向量；FBr为激振力列向量。

2.1.4 箱体子系统阻抗建模

对于复杂箱体而言，通常很难建立实体模型，或者由于自由度过多而无法进行有限元计算，因此只能进行试验研究。此处通过有限元谐响应分析来模拟试验。

箱体的有限元模型，如图5所示。材料为铝合金，密度为2 700 kg/m3，弹性模量为7.1×1010Pa，泊松比为0.33，黏性阻尼比为2%。采用4节点四面体单元进行网格划分，网格大小为5 mm。模型包含75 906个节点，315 412个单元，仅考虑平动方向的自由度。各轴承孔刚性耦合到轴承孔中心节点，箱体底部螺栓孔耦合到螺栓孔中心节点并在螺栓孔处进行固定约束。

图5 箱体有限元模型Fig 5. Finite element model of the housing

采用模态叠加法进行谐响应分析。分别在各轴承孔中心节点的x，y，z方向施加单位激振力，测得各轴承孔中心节点的x，y，z方向的振动位移。

箱体的位移导纳矩阵的每个元素可由式(28)求得

(28)

分别求得箱体导纳矩阵的每个元素后，可以组装出整个导纳矩阵，箱体的阻抗矩阵可由式(29)求得

ZGB=H-1

(29)

箱体阻抗方程可表示为

[ZGB]{XGB}={FGB}

(30)

2.2 “齿轮-轴-轴承-箱体”阻抗综合建模

当求出各子系统的阻抗矩阵后，可根据阻抗综合原理进行阻抗综合。各子系统的耦合关系如图6所示。

图6 各子系统耦合关系Fig 6. Coupling relationship between sub-systems

耦合系统的阻抗动力学方程如下。

(31)

式(31)左端的阻抗矩阵以及右端的激振力列向量是已知的，仅位移列向量是未知的，因此为线性方程组，可以直接求出系统位移。

由于式(31)是在频域，且随频率变化，系统位移的时域解可以通过式(32)求得。

(32)

式中：iGP为齿轮副编号；nGP为齿轮副个数；k为啮合频率的谐波阶次；K为最大谐波阶次；ωiGP为齿轮副的啮合圆频率；j为复数，j2=-1。

2.3 方法验证

由于本文在对齿轮、轴和轴承子系统进行建模时，首先建立了其集中质量模型，然后转换为相应的阻抗模型，因此传动系统的阻抗模型与集中质量模型并无本质区别，区别仅在于求解方法的不同。为了验证本文提出的阻抗模型，针对不考虑箱体的情况，分别采用阻抗模型与集中质量模型计算了随转速变化的啮合力及轴承支反力。传动系统共包含162个自由度，计算了从25 r/min到15 000 r/min的600个不同转速，两种方法均用时30 s左右。啮合力的均方根与轴承力的均方根见图7，阻抗模型与集中质量模型的结果完全一致，说明了阻抗模型的正确性。

本文建立的传动系统与箱体阻抗模型，箱体仅需要轴承孔耦合节点处的导纳，可以方便地将传动系统与箱体进行耦合，而集中质量模型由于箱体自由度过多，很难进行传动系统与箱体的耦合计算。但阻抗模型仅适用于线性定常系统的稳态分析，因此并不适用于齿轮的非线性动力学分析，而集中质量模型可以考虑间隙等非线性因素。

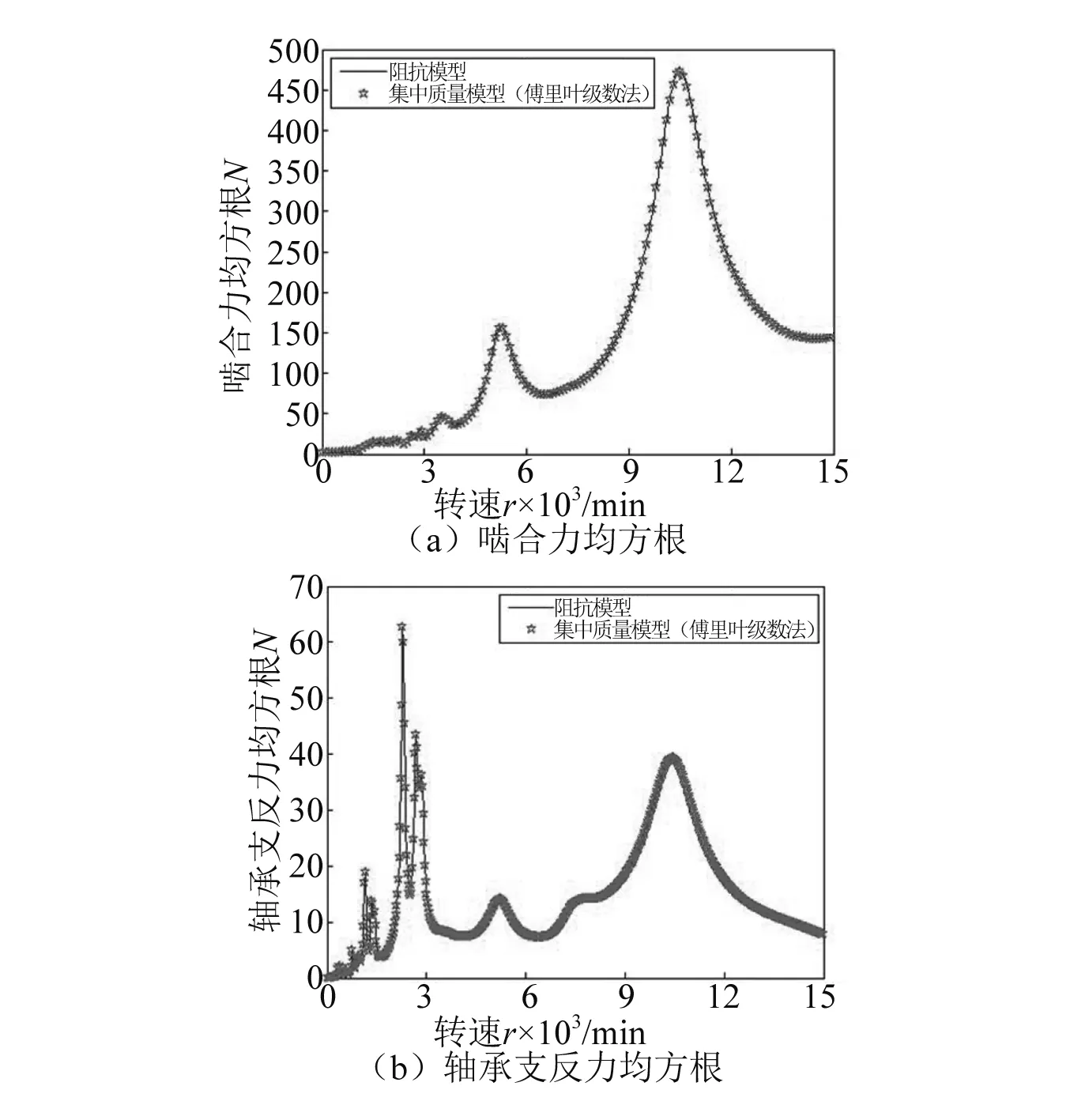
图7 模型验证Fig 7. Model validation

3 箱体柔性对传动系统影响分析

3.1 箱体柔性对系统固有频率的影响

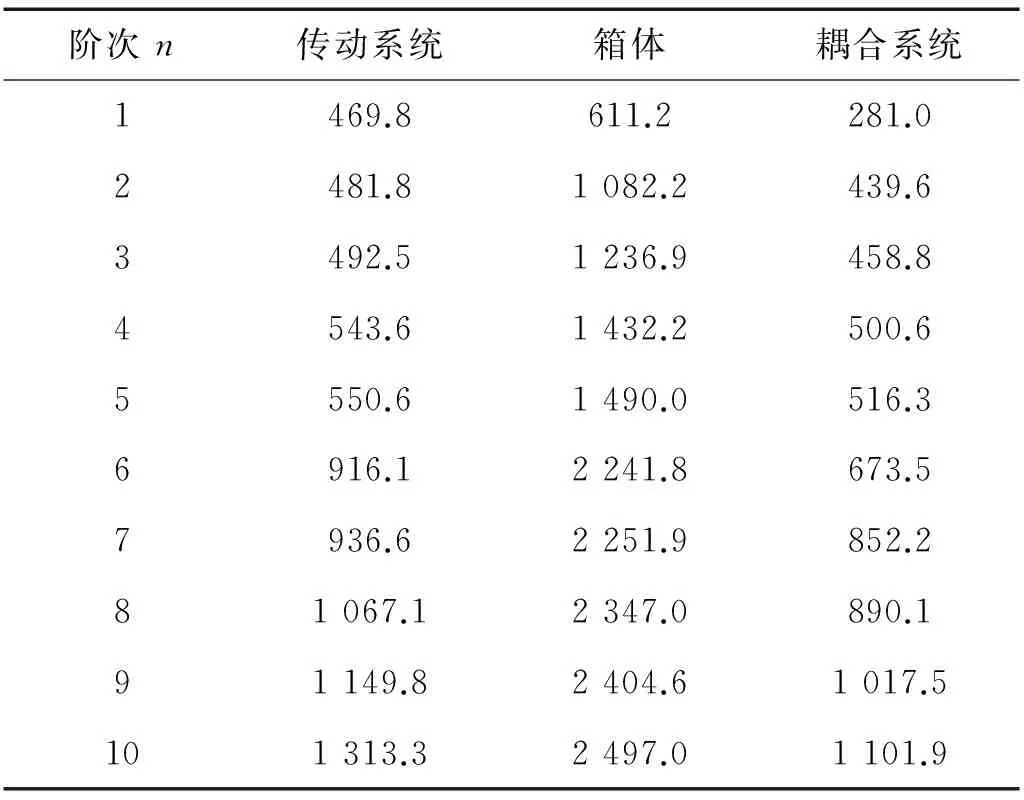
“齿轮-轴-轴承-箱体”耦合系统的阻抗矩阵求解完毕后，可以通过矩阵求逆得到系统的导纳矩阵。导纳矩阵的每一个元素都是随频率变化的函数，频率-导纳曲线的峰值代表了系统的固有频率。以0.1 Hz为步长进行扫频，得系统的前十阶固有频率见表2。由表2可知，耦合箱体后系统的固有频率明显降低了，这是由于箱体增加了传动系统的柔性。

表2 系统固有频率

Tab.2 System natural frequency Hz

3.2 箱体柔性对齿轮啮合力影响

系统动响应求解完毕后，可根据式(33)计算齿轮副的动态传递误差。

DTE=VPXm

(33)

式中：DTE为动态传递误差；VP为投影向量；Xm为啮合副单元的振动位移。

齿轮副的动态啮合力可由式(34)计算

(34)

分别求得不同转速下耦合箱体前后齿轮副的动态啮合力，并进行对比，随转速变化的啮合力均方根如图8 (a)所示。耦合箱体前的两个主共振峰分别对应系统第15阶固有频率及它的1/2倍频，耦合箱体后由于箱体柔性的影响，系统出现更多的固有频率，导致主共振峰分别对应耦合系统的第37阶固有频率及它的1/2倍频。考虑箱体柔性以后，两个主共振峰的峰值由472.8 N和157.0 N变为453.9 N和151.1 N，降幅达到了4.0%和3.8%。

箱体对啮合力的影响可由下式计算

(35)

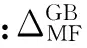
不同工作转速下，箱体柔性对齿轮副振动的影响如图8 (b)所示。由图可知，在不同的工作转速下，箱体可能增加齿轮的振动，也可能减小齿轮的振动。箱体对齿轮副振动的影响主要在3 000 r/min以下，影响程度可达-48.7%～51.1%。

图8 箱体对齿轮啮合力的影响Fig 8. Influence of housing on gear mesh force

3.3 箱体柔性对轴承支反力影响

当求得系统振动位移后，可根据式(27)求得轴承力，根据反傅里叶变换并将不同频率下的轴承力线性叠加，可得到时域内的轴承支反力。

不同转速下，耦合箱体前后轴承1的轴承支反力均方根如图9 (a)所示。箱体柔性对轴承1的振动有很大的影响：①峰值对应的固有频率发生了变化，原对应第6、8、15阶固有频率的峰值耦合后分别对应第7、9、36阶固有频率；②部分峰值发生了偏移，主共振峰所对应的频率降低了6.6%；③峰值的幅值发生变化，主共振峰的幅值降低了7.2%；④出现了新的峰值，如耦合后第6、17阶固有频率处出现新的峰值。

图9 箱体对轴承支反力的影响Fig 9. Influence of housing on bearing reaction force

箱体对轴承支反力的影响可由下式计算。

(36)

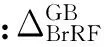
Liu 等的研究表明箱体会增加轴承振动，而贺朝霞等则认为箱体会减小轴承振动，但是他们都仅研究了某几个特殊的工况。不同转速下，箱体柔性对轴承振动的影响程度如图9(b)所示。在某些转速下箱体会增加轴承振动，而在其它转速下会减小轴承振动。箱体对轴承振动的影响主要在5 000 r/min以下，影响程度可达-80.6%～288.3%，这主要是由于共振峰值向左偏移导致的。

3.4 箱体阻抗变化对系统振动的影响

为了研究不同箱体对系统振动的影响，将箱体阻抗分别提高、降低一个量级，并与未耦合箱体的情况进行对比。

不同箱体阻抗对齿轮副啮合力的影响如图10(a)所示。对于刚性箱体(箱体阻抗×10)而言，耦合箱体前后，两个主共振峰的幅值均降低0.4%；对于原始箱体而言，耦合箱体前后，两个主共振峰幅值分别降低4.0%和3.8%；而对于柔性箱体(箱体阻抗×0.1)而言，降幅达到了16.2%和4.7%。耦合箱体后，刚性箱体及原始箱体的主共振转速并未发生明显变化，而柔性箱体的主共振转速降低了3.6%。在不同工作转速下，三种箱体对齿轮啮合力的影响范围分别为-36.1% ～ 29.0%，-48.7% ～ 51.1%以及-49.6% ～ 74.6%。说明柔性箱体对齿轮振动的影响更加显著。

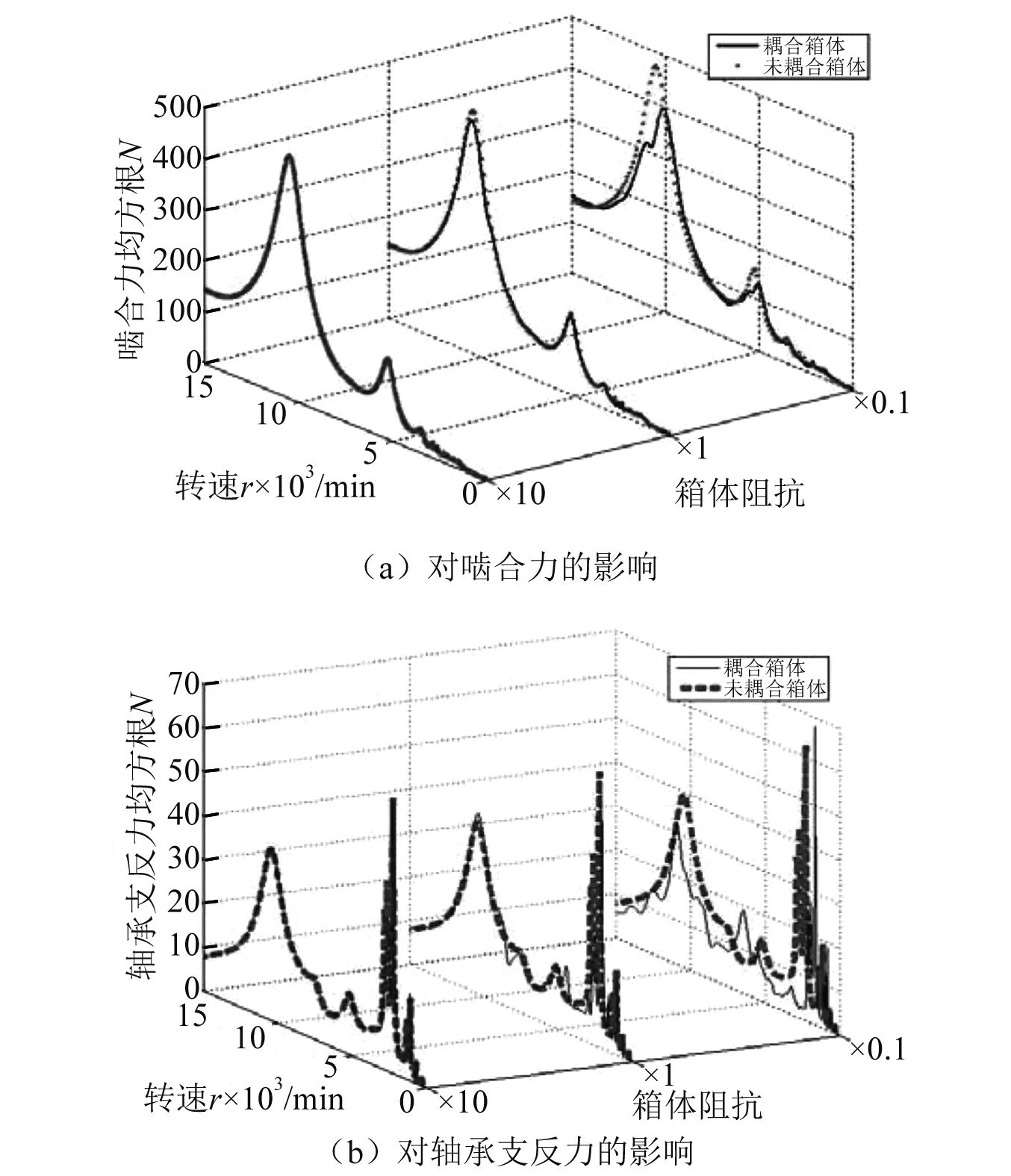
图10 不同箱体阻抗对系统振动的影响Fig 10. Influence of different housing impedances on system vibration

不同箱体阻抗对轴承支反力的影响如图10(b)所示。对于刚性箱体而言，耦合箱体前后，主共振转速没有发生变化；对于原始箱体而言，耦合箱体后，主共振转速降低了6.6%；对于柔性箱体而言，主共振转速降低了27.4%。对于刚性箱体及原始箱体而言，耦合箱体后，主共振峰值降低了0.6%及7.2%，然而对于柔性箱体，主共振峰值升高了8.3%。不同转速下，这三种箱体对轴承支反力的影响范围分别为-44.9%～49.3%，-80.6%～288.3%和 -95.1%～1 704.8%。说明柔性箱体对轴承支反力的影响更加显著。

4 结 论

本文首次采用阻抗综合法进行齿轮传动与箱体的动力学耦合建模。该方法能实现理论数据与试验数据的混合建模，并具有很快的求解速度。通过对耦合箱体前后系统动态特性的对比，得出以下结论：

(1) 耦合箱体后，系统固有频率降低了。

(2) 箱体柔性对齿轮啮合力波动的影响较小，而对轴承支反力波动的影响较大。

(3) 箱体柔性可能增加轴承振动也可能减小，取决于工作转速。

(4) 刚性箱体对系统振动的影响较小，而柔性箱体对系统振动的影响十分显著。

(5) 阻抗综合法是一种有效的子结构综合法，为齿轮传动系统、箱体、基础的耦合提供了新思路。

[1] 常乐浩, 刘更, 吴立言. 齿轮综合啮合误差计算方法及对系统振动的影响[J]. 机械工程学报, 2015, 51(1): 123-130. CHANG Lehao, LIU Geng, WU Liyan. Determination of composite meshing errors and its influence on the vibration of gear system [J]. Journal of Mechanical Engineering, 2015, 51(1): 123-130.

[2] MOHAMED S A, SLIM B, FAKHER C. An acoustic-structural interaction modelling for the evaluation of a gearbox-radiated noise [J]. Mechanical Sciences, 2008, 50: 569-577.

[3] ABBES M S, FAKHFAKH T, HADDER M, et al. Effect of transmission error on the dynamic behaviour of gearbox housing [J]. The International Journal of Advanced Manufacturing Technology, 2007, 34(3/4): 211-218.

[4] HAMBRIC S A, SHEPHERD M R, CAMPBELL R L. Effects of gears, bearings, and housings on gearbox transmission shafting resonances [C]∥ ASME 2010 International Mechanical Engineering Congress and Exposition. Vancouver:ASME, 2010: 229-238.

[5] RIGAUD E, SABOT J. Effect of elasticity of shafts, bearings, casing and couplings on the critical rotational speeds of a gearbox [J]. Physics, 2007,1230:833-845.

[6] CHOY F K, TU Y K, ZAKRAJSEK J J, et al. Effects of gear box vibration and mass imbalance on the dynamics of multistage gear transmission [J]. Journal of Vibration and Acoustics, 1991, 113(3): 333-344.

[7] 林腾蛟, 蒋仁科, 李润方,等. 船用齿轮箱动态响应及抗冲击性能数值仿真[J]. 振动与冲击, 2007, 26(12): 14-17. LIN Tengjiao, JIANG Renke, LI Runfang, et al. Numerical simulation of dynamic response and shock resistance of marine gearbox [J]. Journal of Vibration and Shock, 2007, 26(12): 14-17.

[8] ZHU C C, XU X, LIU H, et al. Research on dynamical characteristics of wind turbine gearboxes with flexible pins [J]. Renewable Energy, 2014, 68: 724-732.

[9] 贺朝霞, 常乐浩, 刘岚. 耦合箱体振动的行星齿轮传动系统动态响应分析 [J]. 华南理工大学学报(自然科学版), 2015 (9): 128-134. HE Zhaoxia, CHANG Lehao, LIU Lan. Dynamic response analysis of planetary gear transmission system coupled with gearbox vibrations [J]. Journal of South China University of Technology(Natural Science Edition), 2015 (9): 128-134.

[2] 高红斌, 卢改林, 高琨, 等. 单级悬臂泵轴的动态分析与改进设计[J]. 流体机械, 2011(7):45-49. GAO Hongbin,LU Gailin,GAO Kun,et al. Dynamic analysis and improved design of single-stage cantitlever pump shaft[J].Fluid Machinery,2011(7):45-49.

[3] 刘厚林,徐欢, 吴贤芳, 等. 基于流固耦合的导叶式离心泵强度分析[J]. 振动与冲击, 2013,32(12):27-30. LIU Houlin,XU Huan,WU Xianfang,et al. Stength analysis of a diffuser pump based on fluid-structure interaction[J].Journal of Vibration and Shock,2013,32(12):27-30.

[4] 荆丰梅, 肖钢,熊志民. 潮流能水轮机单向流固耦合计算方法[J]. 振动与冲击, 2013, 32(8):91-95. JING Fengmei,XIAO Gang,XIONG Zhimin. Calculation method of fluid and structure interaction in a vertical-axis ticlal current turbine[J]. Journal of Vibration and Shock,2013,32(8):91-95.

[5] 黄文俊, 朱晓农, 于洋, 等. 离心风机转子临界转速计算方法的对比分析[J]. 流体机械, 2014(10):37-40. HUANG Wenjun,ZHU Xiaonong,YU Yang,et al. Comparative analysis of calculation method for critical rotating speed of centrifugal fan rotor[J].Fluid Machinery,2014(10):37-40.

[6] 潘旭, 李成, 铁瑛, 等. 轴流泵叶片流固耦合强度分析[J]. 水力发电学报, 2012(4):221-226. PAN Xu,LI Cheng,TIE Ying,et al. Strengh analysis of fluid-solid coupling of axial flow pump blades[J]Journal of Hydroelectric Engineering,2012(4):221-226.

[7] 刘厚林, 徐欢, 王凯, 等. 基于流固耦合的余热排出泵转子模态分析[J]. 流体机械, 2012(6):28-32. LIU Houlin,XU Huan,WANG Kai,et al. Modal analysis for rotor of residual heat removal pump based on fluid-structure interaction[J]. Fluid Machinery, 2012(6):28-32.

[8] 刘建瑞, 陈斌, 张金凤, 等. 余热排出泵水中模态分析[J]. 排灌机械工程学报, 2015, 33(4):290-295. LIU Jianrui,CHEN Bin, ZHANG Jinfeng,et al. Mode analysis for rotor of residual heat removal pump in water[J]. Journal of Drainage and Irrigation Machinery Engineering,2015,33(4):290-295.

[9] 施卫东, 郭艳磊, 张德胜, 等. 大型潜水轴流泵转子部件湿模态数值模拟[J]. 农业工程学报, 2013, 29(24):72-78. SHI Weidong, GUO Yanlei, ZHANG Desheng, et al. Numerical simulation on modal of large submersible axial-flow pump rotor[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(24): 72-78.

[10] 朱利, 杨昌明, 郑军, 等. 基于流固耦合的轴流泵叶轮结构分析[J]. 流体机械, 2013(3):20-23. ZHU Li,YANG Changming,ZHENG Jun,et al. Structure analysis of axial flow pump impeller based on fluid-solid coupling[J]Fluid Machinery,2013(3):20-23.

[11] 袁寿其, 徐宇平, 张金凤, 等. 流固耦合作用对螺旋离心泵流场影响的数值分析[J]. 农业机械学报, 2013(1):38-42. YUAN Shouqi,XU Yuping,ZHANG Jinfeng, et al. Numerical analysis for effect of fluid-structure interaction on flow field in screw centrifugal pump[J]Transactions of the Chinese Society for Agricultural Machinery,2013(1):38-42.

[12] 陈志平, 章序文, 林兴华,等. 搅拌与混合设备设计选用手册[M]. 北京: 化学工业出版社, 2004.

[13] 张钰.水介质中的转子动力学建模及模态分析研究[D]. 武汉：华中科技大学,2013.

Influence of housing flexibility on the dynamic characteristics of gear transmission systems

REN Yafeng1, CHANG Shan2, LIU Geng1, WU Liyan1

(1. Shaanxi Engineering Laboratory for Transmissions and Controls,Northwestern Polytechnical University, Xi’an 710072, China;2. Harbin 703 Research Institute, Harbin 150036, China)

The impedance models of gear, shaft, bearing and housing were built respectively, and the impedance synthesis approach was adopted to establish a gear-shaft-bearing-housing coupled dynamics model. Taking a single-stage helical gear pair gearbox as an example, the natural frequency of “gear-shaft-bearing-housing” system was computed, and the gear dynamic mesh force and bearing dynamic reaction force under the time-varying mesh stiffness excitation were obtained. A comparison between the coupled configuration and the uncoupled case shows that: the coupling of housing reduces the system natural frequencies; the influence of housing compliance on the bearing reaction force is more prominent than that on the gear mesh force; whether the gearbox housing will reduce or intensify the system vibration depends on the operation speed.

gear dynamics; housing flexibility; coupled vibration; impedance synthesis

国家自然科学基金重点项目(51535009)；高等学校学科创新引智计划资助(B13044)

2016-03-30 修改稿收到日期： 2016-06-13

任亚峰 男，博士生，1990年生

刘更 男，教授，博士生导师，1961年生

TH113

A

10.13465/j.cnki.jvs.2017.14.013