基于小波总能量相对变化的结构损伤识别
2017-07-19项贻强郏亚坤
项贻强,郏亚坤
(1. 浙江大学 建筑工程学院,杭州 310058; 2. 浙江大学 唐仲英传感材料及应用研究中心,杭州 310058)
基于小波总能量相对变化的结构损伤识别
项贻强1,2,郏亚坤1
(1. 浙江大学 建筑工程学院,杭州 310058; 2. 浙江大学 唐仲英传感材料及应用研究中心,杭州 310058)
桥梁结构损伤伴随着服役期的增加而逐渐加深,寻找合适的损伤识别方法则是桥梁工作者必须面对的问题。通过对测点处动态响应信号进行离散小波变换,并计算各测点处的小波总能量,以结构未损伤状态为基准,提出了一种基于小波总能量相对变化的损伤识别方法,并以一两端固支梁为例,进行了损伤识别应用及有限元模型验证,结果表明,提出的损伤识别指标能够准确判断损伤的存在和定位损伤,且对损伤程度具有敏感性,对噪音污染、小波种类和分解尺度数有鲁棒性,并能够根据加速度、速度和位移信号的分析处理进行损伤判定,可用于桥梁结构的损伤识别。
桥梁工程;离散小波变换;小波总能量;损伤指标;识别
损伤可以定义为结构原始几何特征、材料特性的偏差,其会导致结构中多余应力、位移或振动[1]。结构损伤本质上是结构局部刚度和质量的改变,反映在结构动力特性上是模态参数的变化[2]。伴随着外界荷载的变化和桥梁服役期的增加,桥梁结构性能出现退化,快速准确的识别损伤存在、定位损伤部位并分析损伤程度是摆在桥梁工作者面前一个关键的问题。近年来,基于频率、模态、小波变换的损伤识别方法越来越多的被广大学者研究和应用。
振型曲率法、模态置信准则、增强模态置信准则和柔度矩阵变化法是基于振型模态的损伤识别方法的代表。Nie等[3]通过实验验证当测试模态形状只存在0.5%的噪音时,四种基于模态形状的损伤指标不能有效识别试验拱桥结构的裂缝损伤。
基于频率的损伤识别方法分为直接利用频率变化和频率响应函数与其他方法相结合的损伤识别方法。显著的局部损伤对结构自然频率产生的变化很小,尤其对于大型结构,影响更小,而且由于测量和处理误差的存在,很难监测到这些变化[4]。
对于基于小波变换的损伤识别,一般是基于传统接触测量得到模态形状,再通过小波变换处理描述损伤;由于密集采样点布置困难,无法满足轻微损伤识别的要求,同时噪音的影响很可能在测量时归因复杂连接电缆及因传感器冗余对温度、湿度等的敏感性,导致误判的发生[5]。
小波分析具有多分辨率分析的特点,在时域和频域中都有表征信号局部信息的能力,分析时间序列的局部轻微变化,时间窗和频率窗可以根据信号的具体形态动态调整,在低频带中有良好的频域分辨率,高频带有着良好的时域分辨率[6-8]。离散小波变换常跟随多分辨率分析,它给出了一种自适应的时-频或空间-尺度分辨,多个尺度的离散小波变换在一定程度上可以反映信号的时频分布,相对于连续小波变换,可大大减少小波变换的冗余度并减少计算量[9-11]。小波能量是小波变换的一个重要特征,小波统计能量分布的量值图可以用来分析由多频组分构成的非稳态序列[12]。
不同于传统的基于小波变换的损伤识别,本文提出一种基于小波总能量相对变化的桥梁损伤识别方法,首先对测点动态响应信号(加速度、速度和位移)进行离散小波变换获取不同尺度下的小波系数,计算不同尺度下的小波能量,求出不同测点的小波总能量,以结构损伤前后测点处的小波总能量相对变化为损伤指标,该指标对噪音污染、小波种类选择及小波尺度数具有鲁棒性,且对加速度、速度和位移信号等动态信号均能准确识别出损伤位置。开展基于小波总能量相对变化的结构损伤识别的研究,对于后续结构的损伤识别具有重要的作用和意义。
1 基于相对小波总能量变化的损伤识别方法
1.1 离散小波变换及损伤指标定义
相应于母波函数的一组时域信号的连续小波变换定义为
(1)
式中:(Wψf)(a,b)是连续小波变换的小波系数;a和b是尺度和平移参数;ψ*(t)是母波ψ(t)的共轭复数。
(Wψf)(a,b)=
(DWψf)(j,k)=
(2)
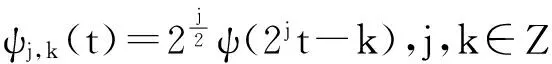
MATLAB中有一维离散小波变换工具箱,对信号进行离散小波变换时,首先要进行小波分解,小波系数包含在小波分解结果中,具体如下:
[C,L] = wavedec(X,N, ‘wname’)
X为待分析信号,N为小波分解尺度,‘wname’为选取的小波种类,C为小波分解向量,L为标签向量。以N阶尺度下的小波分解为例,其结构如图1所示。
AN为最高阶尺度近似,Di(i=N,N-1,…,1)为各尺度下的细节。如果信号长度为L,那么AN有L/2N个小波系数,Di有L/2i个小波系数[13]。如图1所示,小
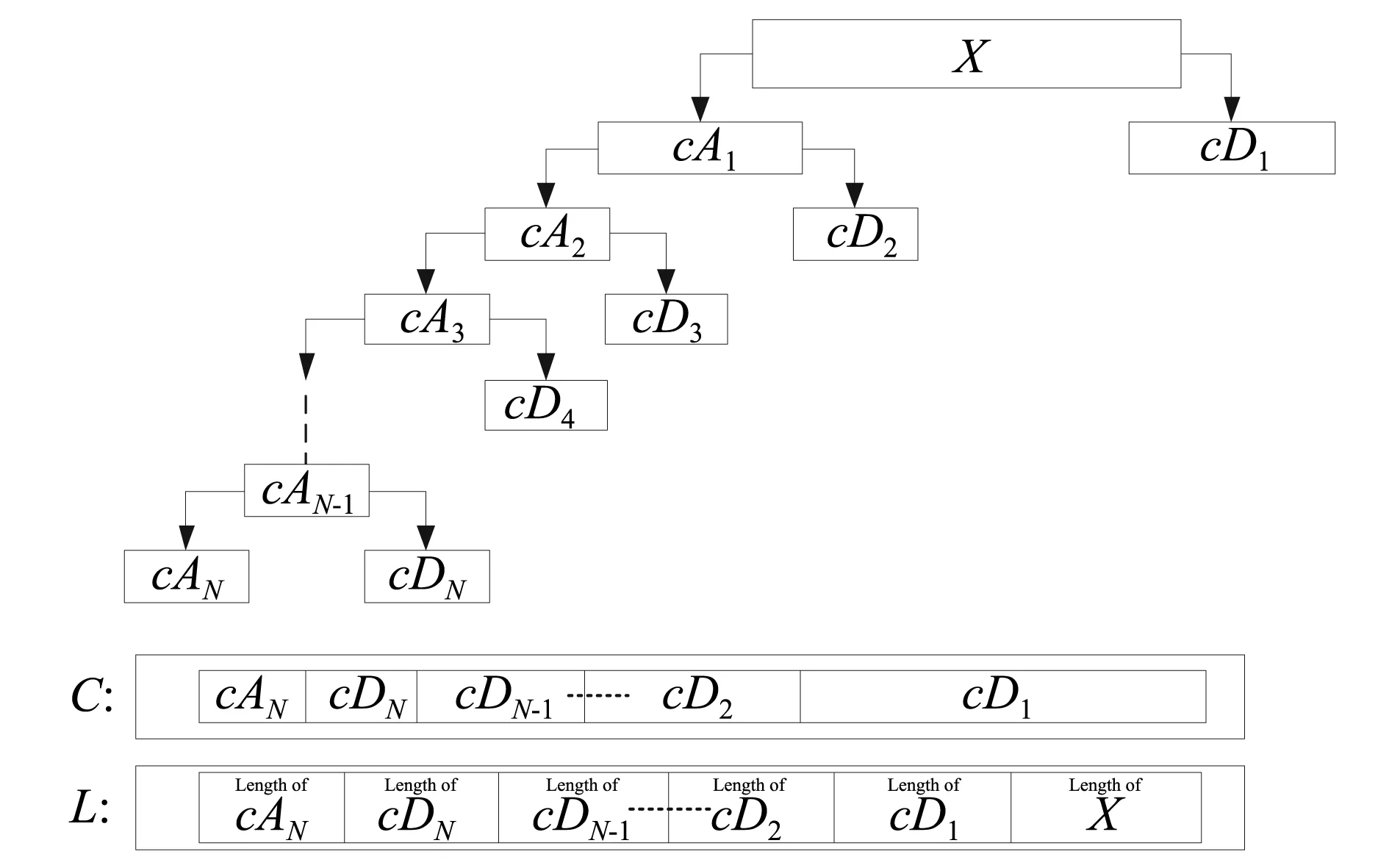
图1 N阶尺度下小波分解示意图Fig.1 The wavelet decomposition at N scales
波分解向量C可以表示为
C=[C1,C2,C3,…,CN+1]=[cAN,cDN,cDN-1,…,cD1]
(3)
MATLAB中对信号进行离散小波变换后的C为一个列向量,需要按照式(3)的形式对小波系数进行重构,使C矩阵的每一列对应不同尺度的近似和细节小波系数。
每个子带Ci(i=N+1,N, …, 1)的小波能量为子带内所有小波系数能量的总和,如式(4)所示[14]
(4)
信号的小波总能量为各个尺度下的小波能量的总和,如式(5)所示
(5)
在结构上合理布置测点,获取结构的动态响应信号。若存在损伤,损伤处动态响应信号(加速度、位移或速度信号等)会更加紊乱,小波系数变化明显,导致小波能量增大,损伤位置处的Etot, dam相对于损伤前该位置处的Etot, undam增加,且变化最大,反之未损伤处的小波总能量变化较少,故可根据测点处小波总能量在损伤前后的相对变化作为损伤指标,判断损伤的存在,并对损伤进行定位识别。
DSI=(Etot, dam-Etot, undam)/Etot, undam
(6)
式中:ifDSI<0,取DSI=0。
损伤位置处的DSIdam比两侧临近测点处的DSI大,由此可以准确判断损伤位置。
1.2 基于小波总能量相对变化的损伤识别步骤
损伤识别程序是基于MATLAB平台编程,运用MATLAB对动态响应信号进行分析和处理,具体步骤如图2所示。
2 有限元模型验证
2.1 有限元模型简介
如图3所示,分析梁为3 m固支梁,材料选用C35混凝土(弹性模量E=3.15×104MPa,容重γ=25 kN/m3),截面采用0.1 m×0.1 m的矩形截面[15],损伤采用截面宽度不变,高度折减的方式进行模拟。荷载采用冲击荷载的形式施加,如图4所示,运用Midas Civil中的时程分析进行冲击荷载的施加,冲击荷载采用文献[16]中形式(见图4),不考虑噪音,并施加在节点4处,采样频率2 000 Hz,分析时长2.408 s,振型阻尼0.05,对梁进行线性瞬态分析。动态响应信号测点一般布置在除去两端支点处的等分点处,另外可根据识别的精度需要进行加密,测点布置数量越多,识别精度越大,定位损伤的效果越好。
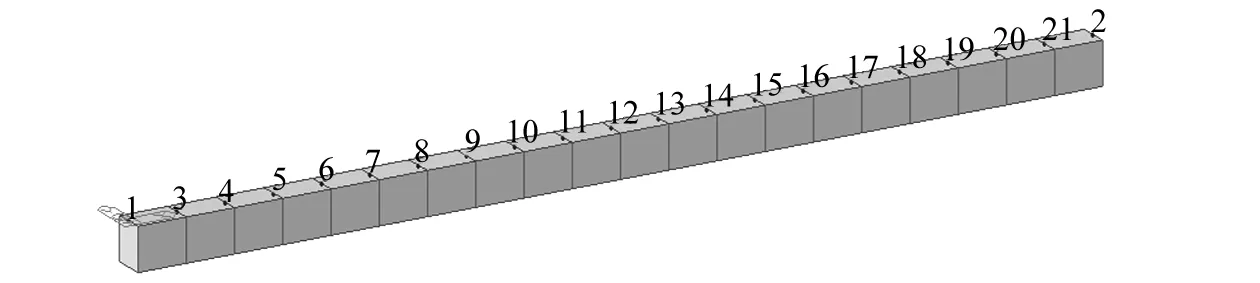
图3 冲击荷载作用下梁的有限元模型Fig.3 Finite element model for analyzing bridge under impact load
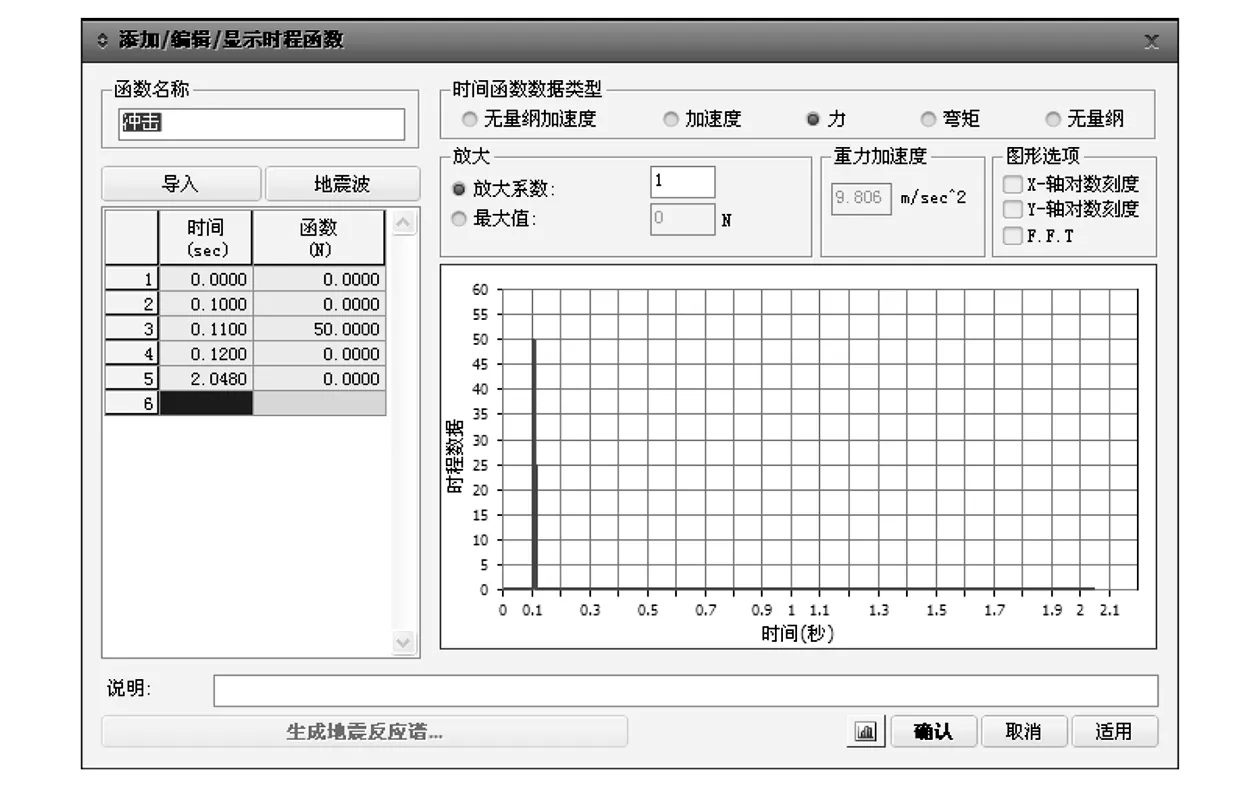
图4 冲击荷载时程数据Fig. 4 Time-history data of the impact load
2.2 损伤类型
损伤分为单个损伤和多损伤,单个损伤又可以分为单个节点处损伤和单个单元损伤。单个节点损伤导致单个测点处的DSI值比其它位置明显较大,单个单元处的损伤会导致该单元上的两个节点处的损伤指标DSI比其它位置处的DSI值明显较大,据此可以区分单个单元损伤和节点损伤。
由此设置以下三种损伤类型:
损伤1# 单元6损伤,损伤程度30%。
损伤2# 节点7处截面损伤,通过对节点7处截面施加3 mm厚的缺口模拟,损伤程度30%。
损伤3# 节点7和节点11损伤,损伤程度30%。
以损伤1#为例,对固支梁中单元6(节点7与节点8之间)施加损伤,损伤程度为30%,此时单元6的截面为:0.07 m×0.1 m,损伤前后固支梁的频率变化如表1所示,损伤前后频率变化最大仅为4%,无法采用频率法判断损伤的存在及定位损伤位置。

表1 损伤前后的频率变化分析
2.3 基于小波总能量相对变化的损伤识别结果
如图3所示,固支梁划分为20个单元,除去两端部固支节点,在剩余的19个等分点上布置测点,运用Midas Civil时程分析,可以获取19个节点处的竖向(Z方向)动态响应信号(加速度信号、速度信号及位移信号)。滤波器采用Elliptic,为了得到模型的前4阶模态,移除高阶频率组分对信号处理的影响,设置截止频率为450 Hz,对信号进行滤波处理。Daubechies小波为有限紧支撑的正交小波,时频域局部化能力较强[17],采用小波db1,尺度为8,对动态信号进行小波分解,并进行离散小波变换。

图5 动态时程响应信号(以节点2加速度信号为例)Fig.5 Dynamic response signal (acceleration at node 2)
2.3.1 损伤1#时的损伤识别结果
图6~图8分别给出了以节点加速度、速度及位移等信号进行分析,单元6损伤30%下的识别结果。图中,x为节点编号,DSI为损伤指标值。
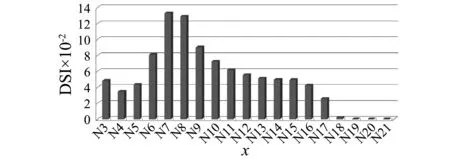
图6 加速度信号下单元6损伤30%的识别结果Fig.6 Detection result for 30% damage of Element 6 using acceleration signal
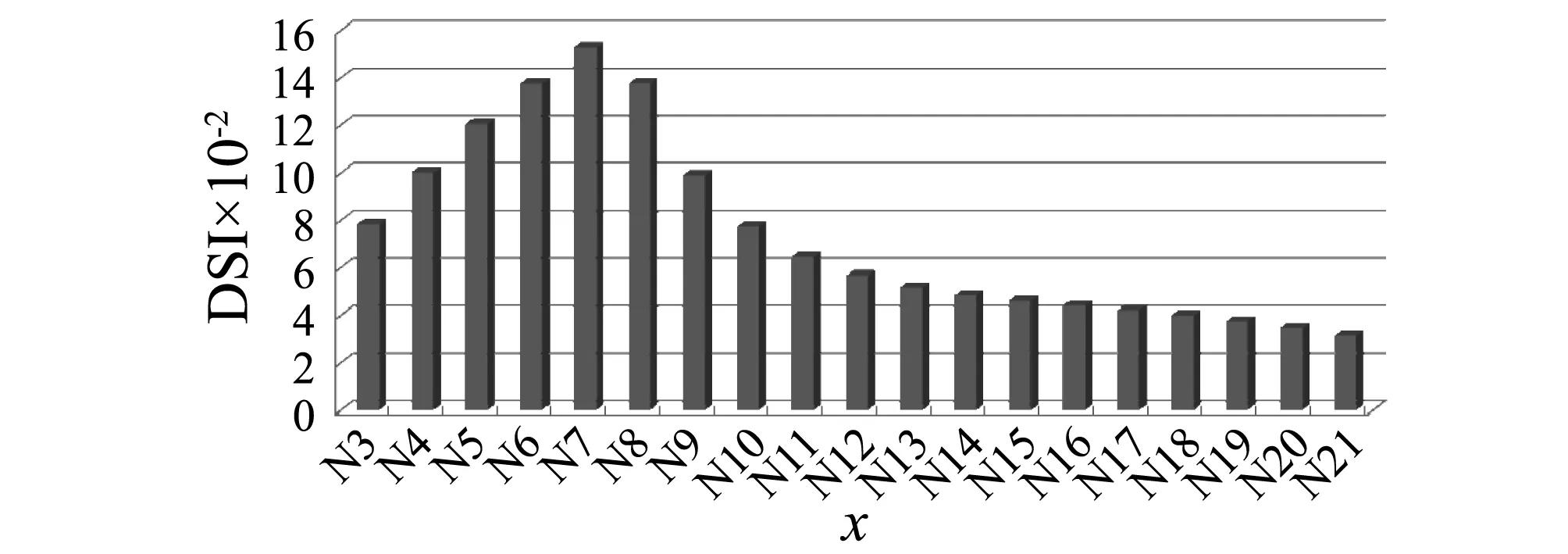
图7 速度信号下单元6损伤30%的识别结果Fig.7 Detection result for 30% damage of Element 6 using velocity signal

图8 位移信号下单元6损伤30%的识别结果Fig.8 Detection result for 30% damage of Element 6 using displacement signal
由图6~图8可知,无论采用加速度信号、位移信号或速度信号,各节点处的DSI分布不均匀,说明损伤存在;又节点7和节点8处的DSI比其他位置的DSI均大,说明损伤发生在节点7和节点8之间的单元上,识别出的预设损伤位置与预设损伤位置相同。因此,采用基于小波总能量相对变化的损伤识别方法可以准确识别出单个单元30%的损伤。
2.3.2 损伤2#时的损伤识别结果
对于节点7处截面3 mm裂缝,以节点加速度、速度及位移等信号进行分析、损伤程度为30%下的损伤识别结果分别如图9~图11所示。
由图9~图11可知,无论采用加速度信号、位移信号或速度信号,各节点处的DSI分布不均匀,说明损伤存在;又节点7的DSI比其他位置的DSI均大,说明损伤发生在节点7处,识别出的预设损伤位置与预设损伤位置相同。因此,采用基于相对小波总能量变化的损伤识别方法可以准确识别出节点30%的损伤。

图9 加速度信号下节点7处损伤30%的识别结果Fig.9 Detection result for 30% damage of Node 7 using acceleration signal

图10 速度信号下节点7处损伤30%的识别结果Fig.10 Detection result for 30% damage of Node 7 using velocity signal
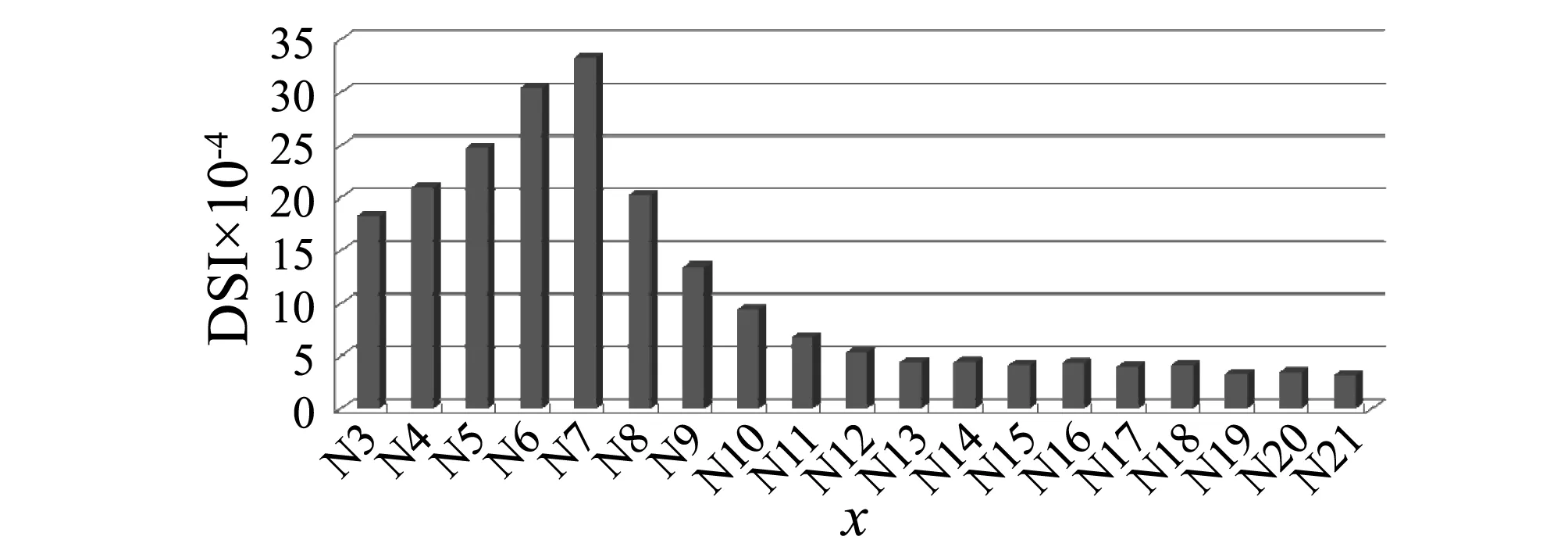
图11 位移信号下节点7处损伤30%的识别结果Fig.11 Detection result for 30% damage of Node 7 using displacement signal
2.3.3 损伤3#时的损伤识别结果
图12、图13、图14分别以节点加速度、速度及位移等信号进行分析,得到节点7和11损伤30%下的识别结果。

图12 加速度信号下节点7和节点11损伤30%的识别结果Fig.12 Detection result for 30% damage of Node 7 and 11 using acceleration signal
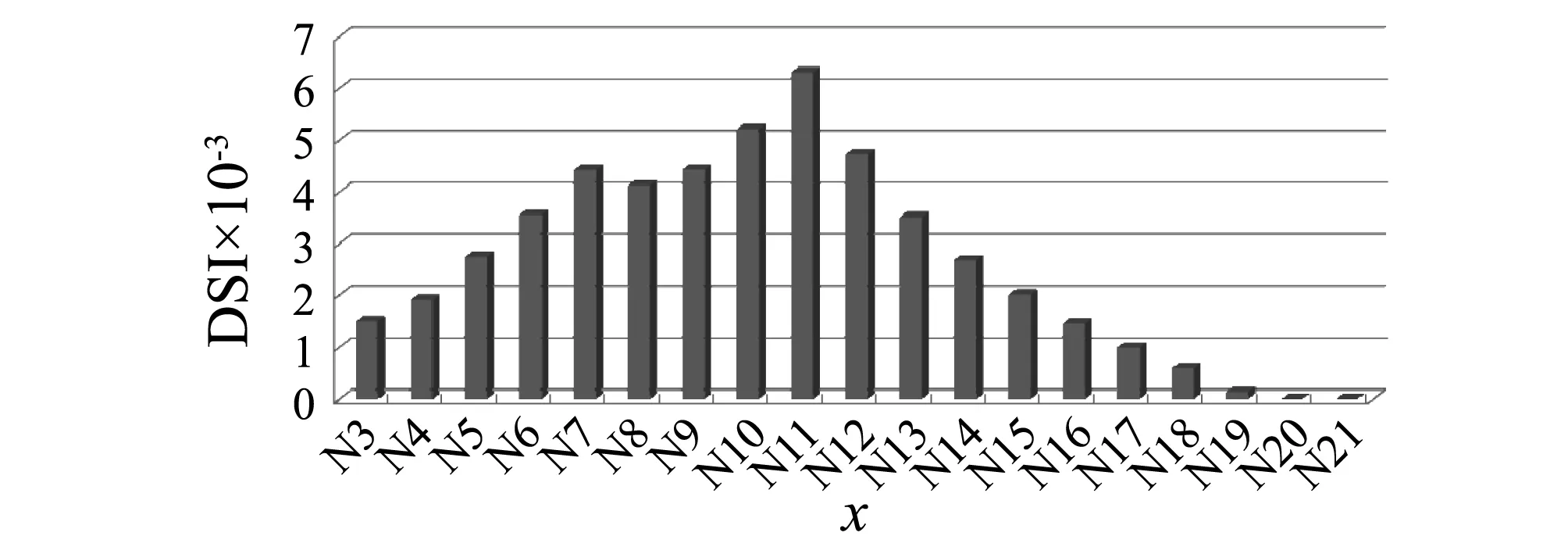
图13 速度信号下节点7和节点11损伤30%的识别结果Fig.13 Detection result for 30% damage of Node 7 and 11 using velocity signal
由图12~图14可知,无论采用加速度信号、位移信号或速度信号,各节点处的DSI分布不均匀,说明损伤存在;且DSI7,DSI11均比其两侧节点处的DSI大,说明损伤存在两个位置,即节点7和节点13存在损伤。
2.4 损伤敏感性分析
以节点加速度信号为例,验证提出的损伤指标对不同损伤程度的敏感性,对节点7处截面3 mm缺口的不同高度模拟不同程度的损伤。图15~图17中,x为节点编号,y为损伤程度,DSI为损伤指标值。

图15 不同损伤程度下的损伤识别结果Fig.15 Damage detection results under different extent of damage
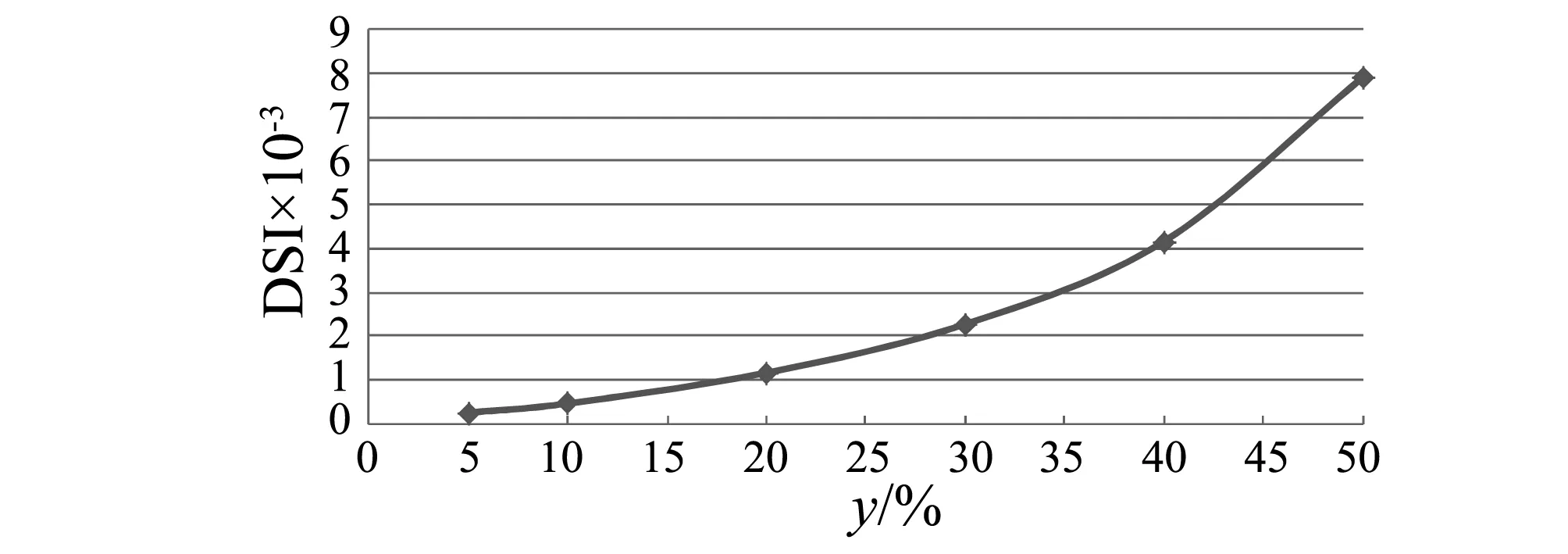
图16 不同损伤程度下节点7处的DSI值Fig.16 DSI value at Node 7 under different extent of damage

图17 节点7处DSI-损伤程度公式拟合图Fig.17 Fitting chart for DSI-damage extent at Node 7
图15给出了5%,10%~50%损伤程度下的损伤指标结果图,发现所提出的损伤指标DSI对5%的小损伤亦是敏感的,能够准确识别出小损伤发生的位置。图16进一步给出了不同损伤程度下节点7处的DSI值,表明随着损伤程度的增大,损伤指标亦不断增大。
通过拟合DSI和损伤程度映射公式,拟合结果如图17所示,其中:
DSI=0.315x5-0.178 7x4+0.035 4x3+0.015 6x2
+0.001 5x+0.000 1 (R2=1)
(7)
定义多项式:
p(x)=0.315x5-0.178 7x4+0.035 4x3+0.015 6x2
+0.001 5x+0.000 1-DSI
(8)
利用MATLAB求解p(x)=0的实数根,若x∈(0,1),则x即为相应的损伤程度。
在单元中构造25%的损伤,计算损伤位置(节点7处)的DSI,代入公式(7),求出相应的损伤程度,与25%比较即可判断损伤估计的准确性。


图18 加速度信号下节点7损伤25%的识别结果Fig.18 Detection result for 25% damage of Node 7 using acceleration signal
3 基于小波总能量相对变化的损伤识别影响因素分析
3.1 噪音信号的影响
由于实际的测试过程中,噪音是无法避免的。因此,可通过对数值模拟动态响应信号施加了一个随机序列来模拟测量数据的噪音污染,即[18]:
(9)

为了验证损伤识别方法对噪音污染的敏感性,对动态响应信号施加三种噪音水平,分别为0.5%,1%和2%噪音水平,分别对单元6和节点7处截面损伤30%下的识别结果进行分析,以加速度信号为例,不同噪音水平下的识别结果如图19和图20所示。
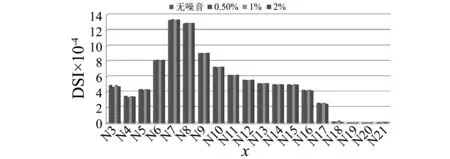
图19 不同噪音水平下单元6损伤30%时识别结果Fig.19 Detection result for 30% damage of Element 6 under different levels of noise
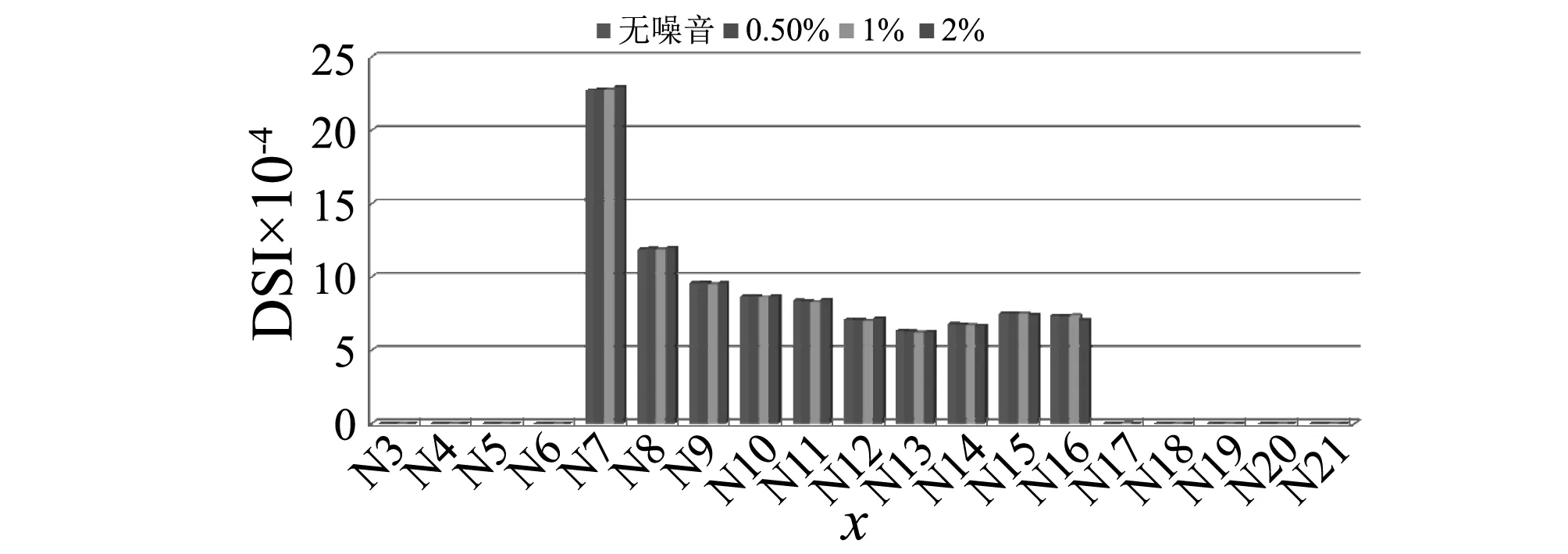
图20 不同噪音水平下节点7损伤30%时识别结果Fig.20 Detection result for 30% damage of Node 7 under different levels of noise
如图19和图20所示,无论对于节点处损伤抑或单元损伤,在不同噪音水平下,提出的损伤指标亦能准确的识别出损伤位置;而且,和无噪音损伤指标值相比,掺杂噪音的信号对应的损伤指标变化微小,提出的损伤指标对噪音污染具有鲁棒性。
3.2 小波种类的影响
离散小波变换取决于小波类型,采用不同的小波得到的小波系数亦不同,本文以节点7损伤30%前后的各节点的加速度响应为分析信号,分别验证损伤指标在haar,db2,sym4,coif3,bior6.8,rbio6.8和dmey等7种不同种类小波下损伤识别结果的鲁棒性。图21中,x为节点编号,y为损伤程度,DSI为损伤指标值。
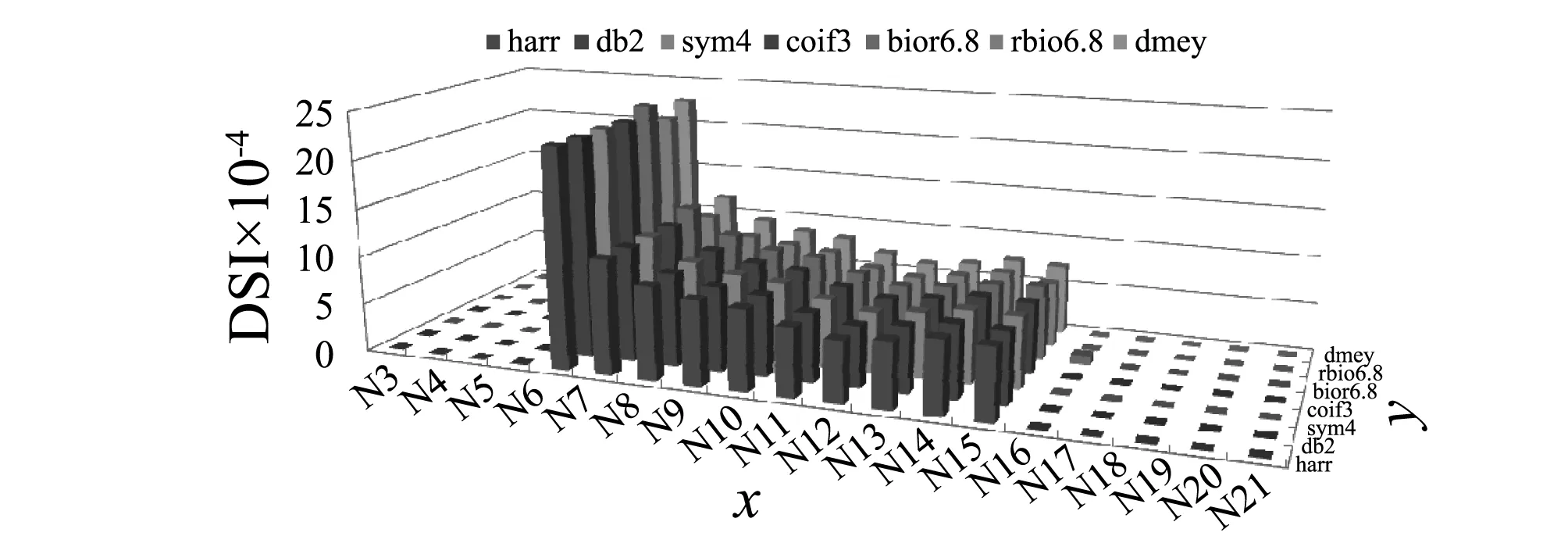
图21 不同种类小波的节点7损伤30%时识别结果Fig.21 Detection result for 30% damage of Node 7 using different kinds of wavelet
如图21所示,采用以上7种不同类型的小波,均能准确的识别出节点7处损伤,且损伤位置处的DSI值变化微小,说明提出的损伤指标对小波类型的选择具有鲁棒性。
3.3 分解尺度数的影响
进行离散小波变换时要确定小波分解尺度,为了研究分解尺度对损伤指标的影响,以节点7处损伤30%下为例,对节点损伤前后的加速度信号进行分析,计算各节点处DSI。图22~24中,x为节点编号,y为分解尺度,DSI为损伤指标值。
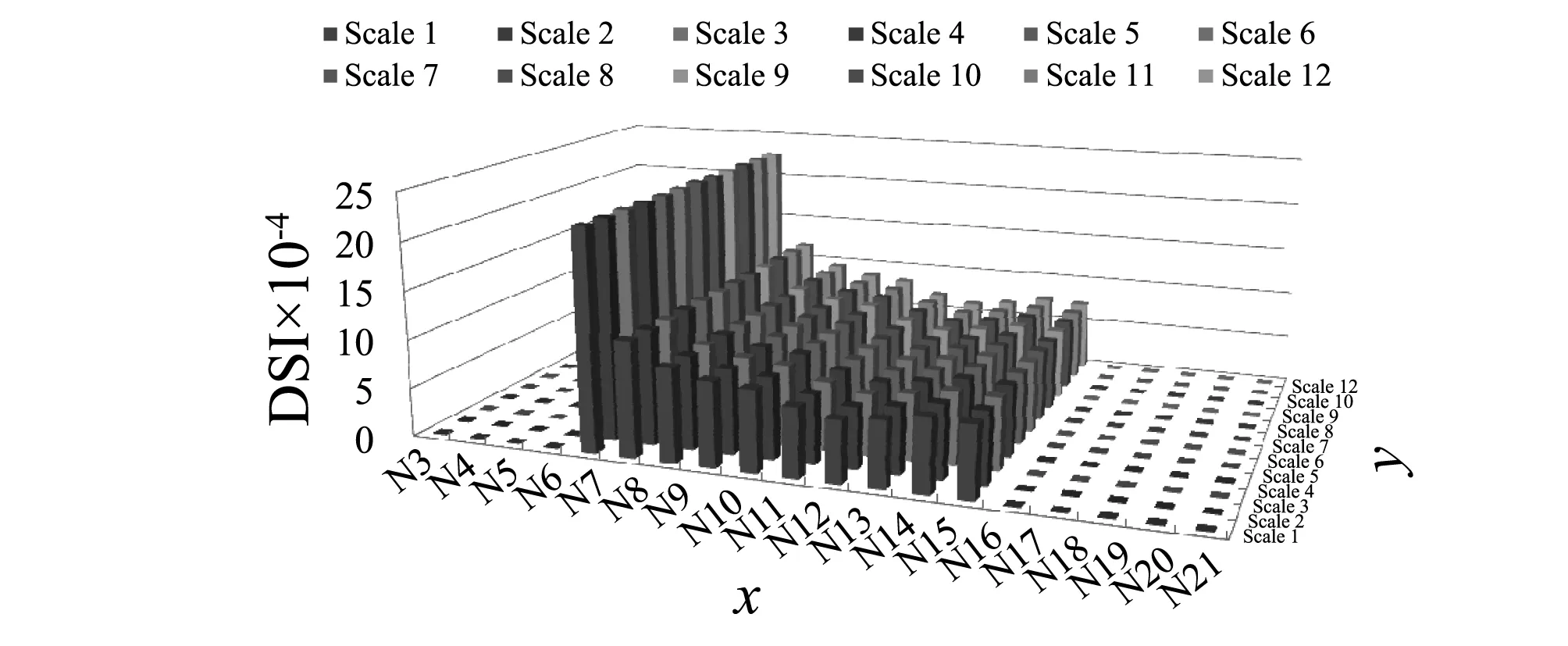
图22 不同尺度下节点7损伤30%的识别结果Fig.22 Detection result for 30% damage of Node 7 under different scale of decomposition
如图22所示,尺度不影响各节点的DSI。原因为:不同的尺度数不改变小波的总能量,只改变小波在特定尺度的分布情况(如图23和图24所示),所以DSI对分解尺度数有鲁棒性。
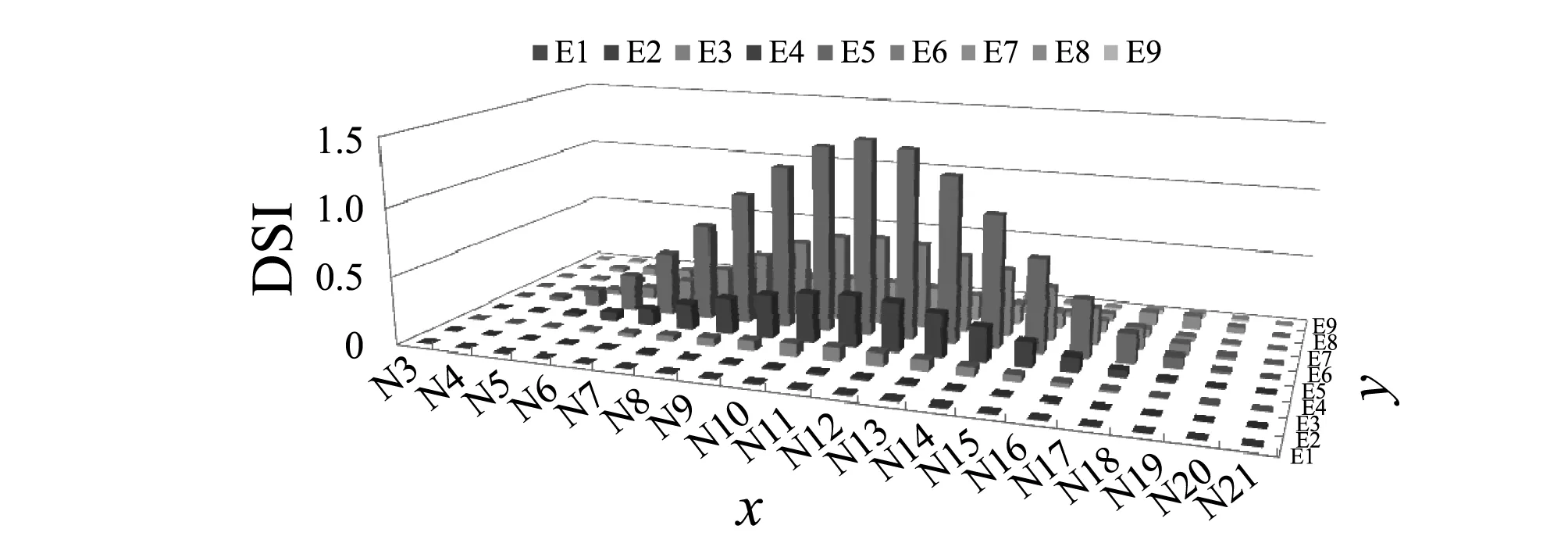
图23 8尺度分解下不同尺度的各节点能量分布Fig.23 The energy distribution of different scale at each node under 8 scale of decomposition
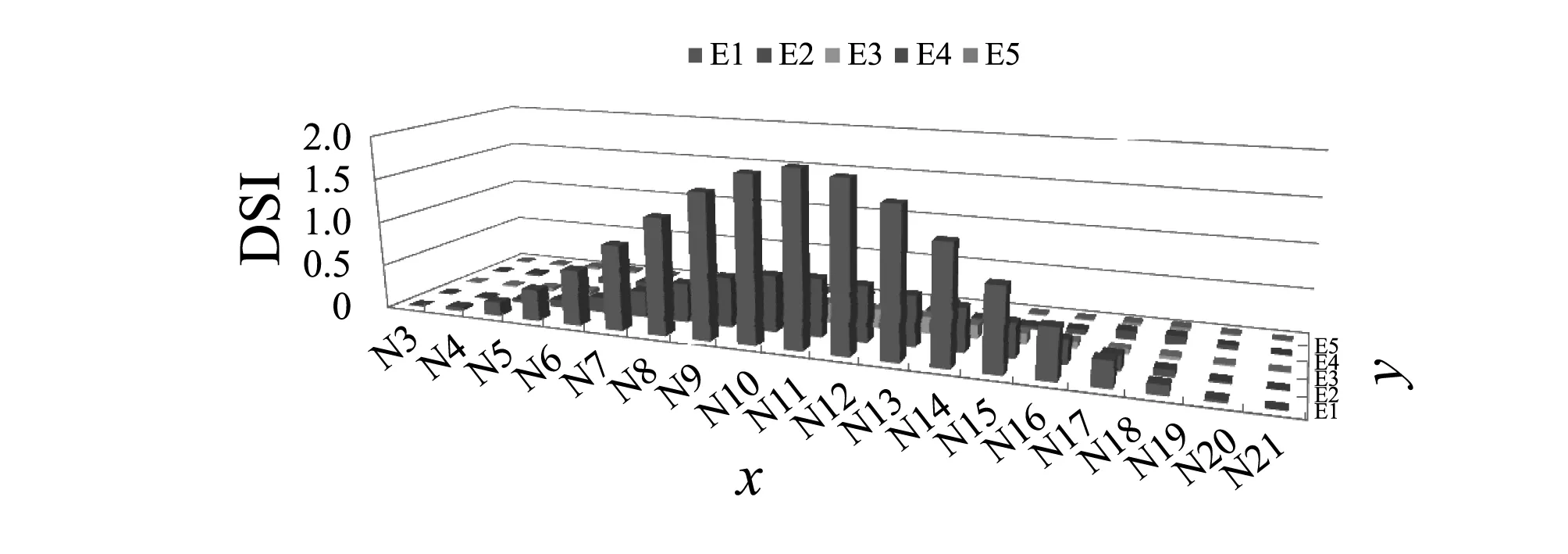
图24 4尺度分解下不同尺度的各节点能量分布Fig.24 The energy distribution of different scale at each node under 4 scale of decomposition
4 结 论
本文通过对结构的动态响应信号进行离散小波变换,计算测点处的小波总能量,以损伤前后测点处小波总能量相对变化值作为损伤指标,提出了一种基于小波总能量相对变化的损伤识别新方法,并以一典型固支梁为例,进行了有限元数值模型分析及验证。从中可以得出如下结论:
(1)基于小波总能量相对变化的结构损伤识别,对动态响应信号的选择具有多样性,可以采用加速度、速度或位移信号进行结构的损伤识别,且能识别结构的单个单元、节点和多处节点的损伤。
(2)基于小波总能量相对变化的损伤指标DSI对小损伤(5%~10%)亦是敏感的,通过拟合损伤指标值和损伤程度的数值公式,可以准确识别出损伤程度。
(3)基于小波总能量相对变化的损伤指标DSI对噪音信号、小波种类和分解尺度数的选择具有鲁棒性。
[1] BANDARA R P, CHAN T H, THAMBIRATNAM D P. Structural damage detection method using frequency response functions[J]. Structural Health Monitoring, 2014, 13(4): 418-429.
[2] 林贤坤,覃柏英,梁兴华. 基于刚度矩阵的桥梁损伤识别研究[J]. 广西工学院学报,2010,21(3):13-18. LIN Xiankun, QIN Boying, LIANG Xinghua. Researches on bridge damage identification based on stiffness matrices [J]. Journal of Guangxi University of Technology, 2010, 21(3): 13-18.
[3] NIE Z, HAO H, MA H. Using vibration phase space topology changes for structural damage detection [J]. Structural Health Monitoring, 2012, 11(5): 538-557.
[4] CHANDRASHEKHAR M, GANGULI R. Structural damage detection using modal curvature and fuzzy logic [J]. Structural Health Monitoring, 2009, 8(4): 267-282.
[5] 郭建,顾正维,孙炳南,等. 基于小波分析的桥梁监测检测方法[J]. 工程力学,2006,23(12):129-135. GUO Jian, GU Zhengwei, SUN Bingnan, et al. Method of bridge health monitoring based on wavelet analysis [J]. Engineering Mechanics, 2006, 23(12): 129-135.
[6] 刘浩,韩晶. MATLAB R2012a完全自学一本通[M]. 北京:电子工业出版社,2013.
[7] SU Yongqing, LIU Hao, YUE Jiguang, et al. Characterization of ionospheric amplitude scintillations using wavelet entropy detrended GNSS data [J]. Advances in Space Research, 2014, 54(11):2172-2183.
[8] 孙增寿,韩建刚,任伟新. 基于小波分析的结构损伤检测研究进展[J]. 振动、测试与诊断,2005,28(2):93-99. SUN Zengshou, HAN Jiangang, REN Weixin. State-of-the-art research and development of wavelet analysis based structural damage detection [J]. Journal of Vibration, Measurement and Diagnosis, 2005, 28(2):93-99.
[9] 何正友,蔡玉梅,钱清泉. 小波熵理论及其在电力系统故障检测中的应用研究[J]. 中国电机工程学报,2005,25(5):38-43. HE Zhengyou, CAI Yumei, QIAN Qingquan. A study of
wavelet entropy theory and its application in electric power system fault detection [J]. Proceedings of the CSEE, 2005, 25(5): 38-43.
[10] 郭建. 基于小波分析的结构损伤识别方法研究[D]. 杭州:浙江大学,2004.
[12] ADDISON P S. The illustrated wavelet transform handbook: introductory theory and applications in science, engineering, medicine and finance[J]. Journal of Physics A: General Physics, 2004, 37(5):1947-1948.
[13] GUN J Y, SOON G L, JOAN C, et al. Decentralized damage identification using wavelet signal analysis embedded on wireless smart sensors [J]. Engineering Structures, 2011, 33(7):2162-2172.
[14] ROSSO O A, MARTIN M T, FIGLIOLA A, et al. EEG analysis using wavelet-based information tools [J]. Journal of Neuroscience Methods, 2006, 153(2):163-82.
[15] 孙增寿,任伟新. 基于小波熵指标的结构损伤检测[J]. 振动、测试与诊断,2008,28(3):233-237. SUN Zengshou, REN Weixin. Structural damage detection based on wavelet entropy index [J]. Journal of Vibration, Measurement and Diagnosis, 2008, 28(3): 233-237.
[16] 刘习军,相林杰,张素侠. 基于小波分析的简支梁损伤识别[J]. 振动、测试与诊断,2015,35(5):866-872. LIU Xijun, XIANG Linjie, ZHANG Suxia. Damage identification of simply supported beam based on wavelet analysis [J]. Journal of Vibration, Measurement and Diagnosis, 2015, 35(5):866-872.
[17] 张敬一,陈龙珠. 基于小波变换的反射波法基桩检测[J]. 振动与冲击,2014,33(6):179-183. ZHANG Jingyi, CHEN Longzhu. Sonic echo test for pile titegrity testing based on wavelet transform [J]. Journal of Vibration and Shock, 2014, 33(6):179-183.
[18] 姜邵飞,胡春明. 基于模态指标与数据融合的钢管混凝土拱桥损伤识别[J]. 振动与冲击,2009,28(12):91-95. JIANG Shaofei, HU Chunming. Structural damage identification based on modal indices and data fusion for an arch bridge of concrete-filled steel tubes [J]. Journal of Vibration and Shock, 2009, 28(12): 91-95.
Damage detection method for structures based on the relative variation of wavelet total energy
XIANG Yiqiang1,2, JIA Yakun1
(1. Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China;2. Cyrus Tang Center for Sensor Materials and Applications, Zhejiang University, Hangzhou 310058, China)
The damage of bridges will be intensified with the increase of service life, so it confronts bridge engineers with searching for an appropriate damage detection method. Applying the discrete wavelet transform to analyze the dynamic response signal at the measuring point, the wavelet total energy can be calculated. Setting the intact structure as a reference state, a detection method based on the relative variation of wavelet total energy was proposed. A case study with respect to a beam (fixed at both ends) was conducted to validate the damage detection method. A finite element model of the beam was established to verify the detection result. It is concluded that: the proposed damage index, which is sensitive to damages, can accurately determine the existence and location of damages. What’s more, it is also shown the index is robust to noises, wavelet types and decomposition scales. The damage detection method proposed can tackle acceleration, velocity and displacement signals to assess damages, and so, can be applied in the damage detection of bridge structures.
bridge structures; discrete wavelet transform; wavelet total energy; damage index; detection
唐仲英基金会及国家自然科学基金项目(51541810)
2016-04-05 修改稿收到日期: 2016-06-07
项贻强 男,博士,教授,1959年生
郏亚坤 男,硕士生,1992年生
TU311.2
A
10.13465/j.cnki.jvs.2017.14.006
