基于在线神经网络算法的混合试验方法

王 涛， 翟绪恒， 孟丽岩， 王 贞

(1. 中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；2.黑龙江科技大学 建筑工程学院，哈尔滨 150022； 3. 哈尔滨工业大学 土木工程学院，哈尔滨 150090)

WANG Tao1,2，ZHAI Xuheng2，MENG Liyan2, WANG Zhen3

(1.Institute of Engineering Mechanics, China Earthquake Administration Key Laboratory of Earthquake Engineering and Engineering Vibration of China Earthquake Administration, Harbin 150080, China; 2. School of Civil Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)

基于在线神经网络算法的混合试验方法

王 涛1,2， 翟绪恒2， 孟丽岩2， 王 贞3

(1. 中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；2.黑龙江科技大学 建筑工程学院，哈尔滨 150022； 3. 哈尔滨工业大学 土木工程学院，哈尔滨 150090)

混合试验是一种将数值模拟与物理试验相结合的新兴结构抗震试验方法，得到了相关研究者们的广泛关注。如何模拟具有强非线性的数值子结构仍是混合试验亟待解决的问题。在传统的离线神经网络基础上提出一种在线学习的神经网络算法，并应用于混合试验中来在线预测数值子结构恢复力。在线学习算法仅利用当前步的系统输入和观测样本，采用递推形式更新每一步的权值和阈值。针对两个自由度非线性结构，分别进行了基于在线学习和离线学习神经网络的混合试验数值仿真。研究表明：与离线学习神经网络算法相比，在线学习神经网络算法具有更好的自适应性，能够有效提高恢复力预测精度和计算效率；基于在线学习神经网络算法的结构混合试验方法可以提高混合试验结果精度。

混合试验；神经网络；在线预测；恢复力

结构混合试验是将试验加载与数值模拟相结合，以较小成本来反映真实结构地震反应的一种新型试验技术。混合试验的数值积分算法[1-2]、加载控制[3-4]、时滞补偿[5]、误差累计[6]、网络协同以及混合试验平台建设[7]等关键技术问题正得到国内、外研究者们的广泛关注，并取得了较大的研究进展。

在传统的混合试验中，通常选取结构或构件中关键部分作为试验子结构进行真实物理加载试验，剩余部分作为数值子结构进行数值模拟。然而，对于一些大型高层建筑以及桥梁结构的混合试验，研究者们会遇到较大的困难。受到作动器数量及试验条件的限制，数值子结构中不可避免会包含一些模拟困难的部分，这些数值部分的模型及模型参数准确程度就会直接影响数值子结构恢复力的计算，进而影响整体混合试验结果。因此，如何提高数值子结构恢复力的计算精度是混合试验亟待解决的问题。

在混合试验中，当数值子结构包含与试验子结构的滞回性能相同构件时，可以充分利用物理加载的观测信息来在线修正数值子结构中相应部分的数值模型或模型参数，即模型更新混合试验方法。Kwon等[8]提出一种多个模型线性叠加的更新方法，试验结果表明该叠加数值模型很好地复制了物理试件的性能。Hashemi等[9]将UKF应用到非线性结构混合试验中，在线更新数值子结构Bouc-Wen模型参数，通过数值模拟和试验验证了模型更新试验方法的有效性。王涛等[10-12]提出一种约束UKF算法，改进的算法可以有效减小了参数识别值前期波动幅度，提高了参数识别收敛速度和模型更新精度，并被应用到防屈曲支撑结构混合试验中。Wu等[13]针对截面恢复力模型，进行了基于UKF的模型更新，并进行了钢框架柱的混合试验验证。上述模型更新方法核心思想是基于假定模型的参数在线更新，因此参数识别效果很大程度上依赖于模型本身的准确性。神经网络(Neural Network，NN)算法[14]不用基于系统具体的非线性数学模型，可以减少数值模型误差所带来的不利影响，具有更好的一般性。

近年来，研究者们将神经网络算法应用在土木工程领域，并取得了较大的研究进展。在时滞控制系统方面，涂建维等[15]提出了采用神经网络预测的方法来减小磁滞效应对振动控制的不利影响。根据过去时刻和当前时刻的结构响应来预测将来时刻的结构响应，有效的补偿了磁滞时间，使控制效果能够接近无磁滞效应的控制效果。周大兴等[16]振动台子结构试验中利用神经网络对作动器的信号进行预测，通过仿真分析验证了方法的有效性。在结构恢复力预测方面，Yang等[17]采用变神经元BP神经网络模拟非线性结构的恢复力模型，进而来预测结构的恢复力。Yun等[18]提出五变量的神经网络输入，并根据输入变量在滞回曲线不同位置的正负号初步应用在恢复力识别中。张健[19]在此研究成果上又增加了三个输入变量，并应用在混合试验中预测数值子结构恢复力。

标准的NN算法采用离线学习方式，这种批量的学习方式并不适用于混合试验中数值子结构恢复力在线预测。为了提高NN算法在线预测的精度和计算效率，本文提出一种基于在线学习方式的神经网络算法，并应用于两个自由度非线性结构混合试验中，以验证改进的NN算法性能及恢复力在线预测混合试验方法的有效性。

1 标准NN算法预测原理

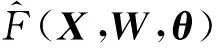
图1 标准神经网络原理图Fig. 1 Schematic diagram of standard NN

图1中系统的输入数据X为n×N的矩阵，具体形式为

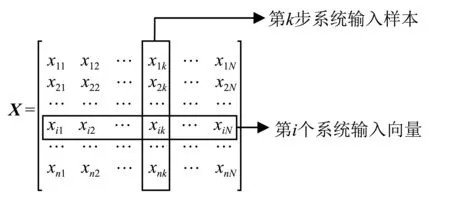
X可分别采用行向量以及列向量表示，即：

X=[x1x2…xi…xn]T=
[x1x2…xk…xN]

式中：xi=[xi1xi2…xik…xiN]为系统第i个输入向量；xk=[x1kx2k…xik…xnk]T为系统第k个输入样本。

同理，系统的观测输出数据Y为m×N维矩阵，具体形式为

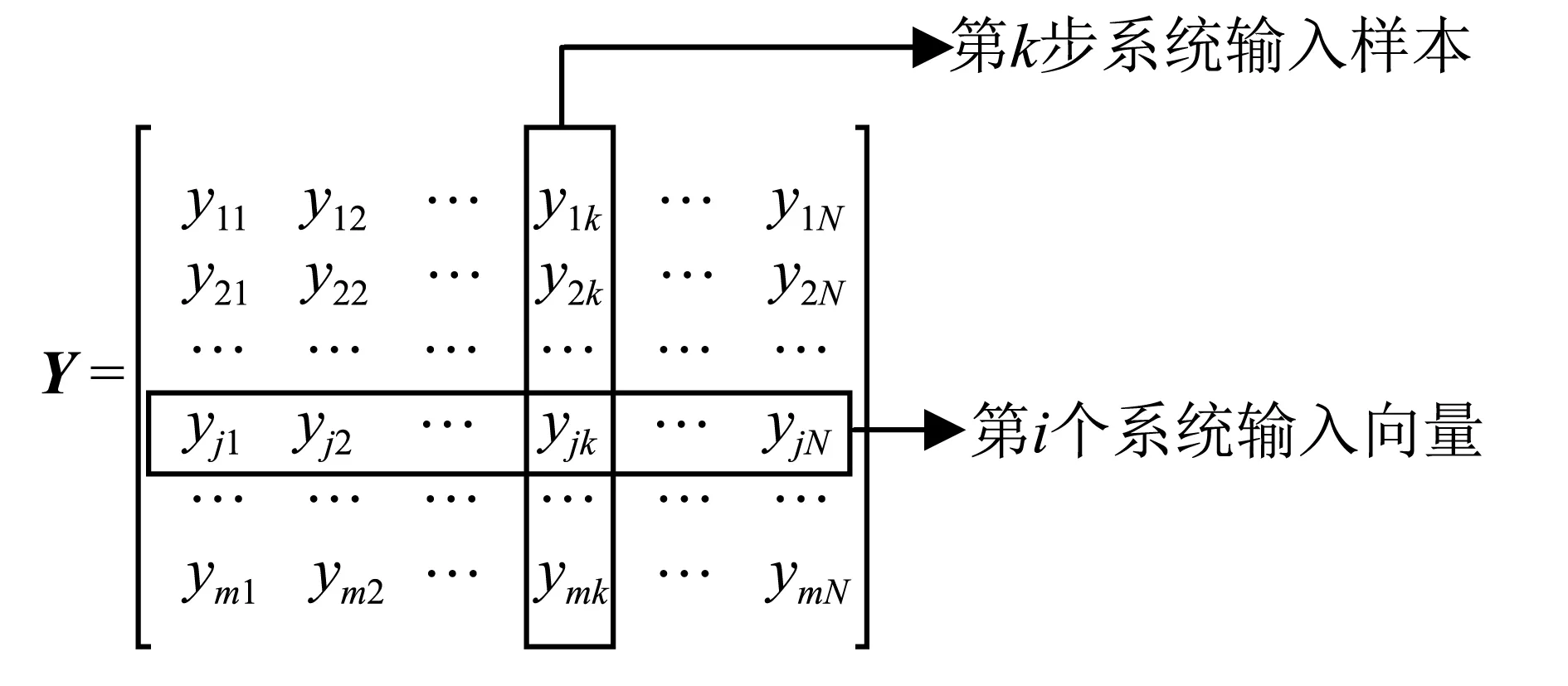
将Y分别以行向量以及列向量表示，即：

Y=[y1y2…yj…ym]T=
[y1y2…yk…yN]

式中：yj=[yj1yj2…yjk…yjN]为系统第j个输出向量；yk=[y1ky2k…yjk…ymk]为系统第k个输出样本。

标准的NN算法虽然可以逼近任意非线性系统，然而当需要进行在线预测应用时就会遇到困难。标准NN算法的学习采用批量训练，即在预测前需要已知系统所有的输入和观测样本。在实际预测过程中，若无法事先获取系统的全部样本时，则要利用当前及之前步已有的全部样本对初始的神经网络进行重复训练。这种训练方式本质上属于离线的学习方法，算法的计算量会随着输入和观测样本数量的逐步增加而显著增大，计算效率随之下降。另外值得注意的是每一步新到的样本会被前面所有步的样本信息逐渐湮没，这将导致训练算法的自适应性变差。结构混合试验本质上是一种在线的闭环控制，试验的每一步加载过程中只能记录到试验子结构当前及之前所有加载步的输入和观测数据。显然，标准的神经网络算法并不适用于数值子结构恢复力的在线预测问题，为此，针对神经网络在学习阶段出现的弊端下面将提出一种在线学习的神经网络算法。

2 在线NN算法

在线学习算法在标准的NN算法基础上主要进行了两个方面改进。一是在线学习算法仅需利用当前第k步的系统输入和观测数据集{xk,yk}对神经网络进行训练，当满足性能目标后，便得到最优的权值Wk和阈值θk。相比而言，标准的NN算法则需要采用当前第k步及之前的所有系统输入和观测数据集{x1,…，xk,y1,…,yk}进行训练，可见改进算法能够降低训练算法的计算负荷，提高计算效率；二是在线学习算法每一步的权值Wk与阈值θk都是基于前一步网络训练完后的权值Wk-1与阈值θk-1进行训练，使得权值与阈值计算具有递推形式。这样算法可以充分利用了前一步的训练结果信息，提高了算法的自适应能力。相比而言，标准NN算法第k步权值Wk与阈值θk均是基于随机的初始权值W0与阈值θ0进行迭代训练。一个典型的三层在线神经网络在第k步的训练示意图如图2所示。

图2 在线NN算法第步训练示意图Fig.2 Training diagram of online NN algorithm at step

在线NN算法的学习阶段包括信号的正向传播和误差的反向传播两个过程。第k步样本输入后的训练迭代过程具体如下:

(1)信号的正向传播

隐含层的输入Uk为所有输入xk的加权之和，即

Uk=Wk(1)xk-θk(1)

(1)

设隐含层的激活函数为g(•)，则隐含层的输出Vk为

Vk=g(Uk)

(2)

输出层的输入Zk为所有隐含层的输出Vk加权之和，即

Zk=Wk(2)×Vk-θk(2)=Wk(2)g(Uk)-θk(2)=
Wk(2)g(Wk(1)xk-θk(1))-θk(2)

(3)

设输出层的激活函数为h(•)，则输出层的输出Dk为

Dk=h(Zk)=h(Wk(2)Vk-θk(2))=
h(Wk(2)g(Wk(1)xk-θk(1))-θk(2))

(4)

(2)误差的反向传播

相比离线学习的NN算法，在线算法不需要记忆全部的训练样本，重新定义在线学习算法在第k步的目标误差性能函数Ek设为

(5)

进行误差反向传播时，将目标误差性能函数分别对各层的连接权值与阈值进行求偏导，得到当前第k步第r次迭代下的权值与阈值的改变量，进而调整第r+1次权迭代后的权值与阈值。每当信号正向输出与期望输出的误差达不到目标误差时，便开始进行权值的反向调整，如此循环下去，直至系统输出达到预测的目标误差要求或最高迭代次数为止。隐含层到输出层当前权值的改变量

考虑在由元件C1、C2构成的并联系统中，如何配置负载冗余元件R使系统可靠性更高，假设X1,X2,Y服从参数为λ1、λ2、λ的指数分布，比较以下两个系统的寿命：

(6)

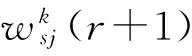
(7)

(8)

(9)

阈值的修正方法同上，此处不再阐述。

经过多次迭代后，此时计算得到的权值矩阵Wk(1)、Wk(2)和阈值矩阵θk(1)、θk(2)则为第k步的最优值，从而在线神经网络有了即时预测的能力。当第k+1步的输入数据与观测样本到来后，网络中权值与阈值的初始值分别为前一步的Wk(1)、Wk(2)、θk(1)、θk(2)，利用目标误差Ek+1对权值与阈值进行再次迭代，最终得到第k+1步时最优的权值矩阵Wk+1(1)、Wk+1(2)和阈值矩阵θk+1(1)、θk+1(2)，如此递推下去，直至试验系统样本输入完毕。在线BP神经网络权值阈值递推关系以及训练流程示意图分别如图3和图4所示。

3 基于在线NN的混合试验方法

3.1 基于在线NN的混合试验原理

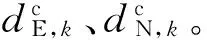
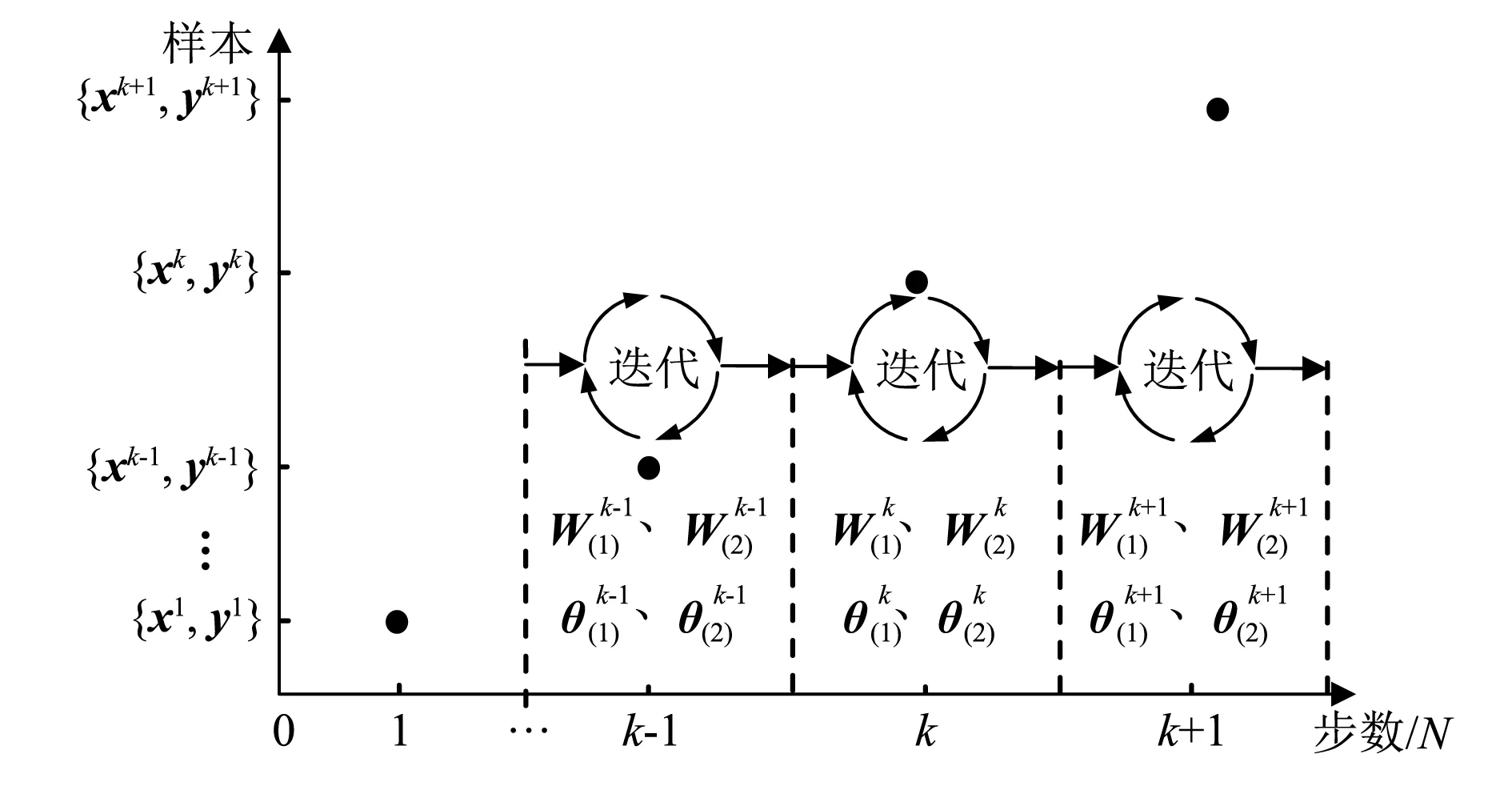
图3 权值与阈值递推关系图Fig.3 Recursive relation of weights and thresholds

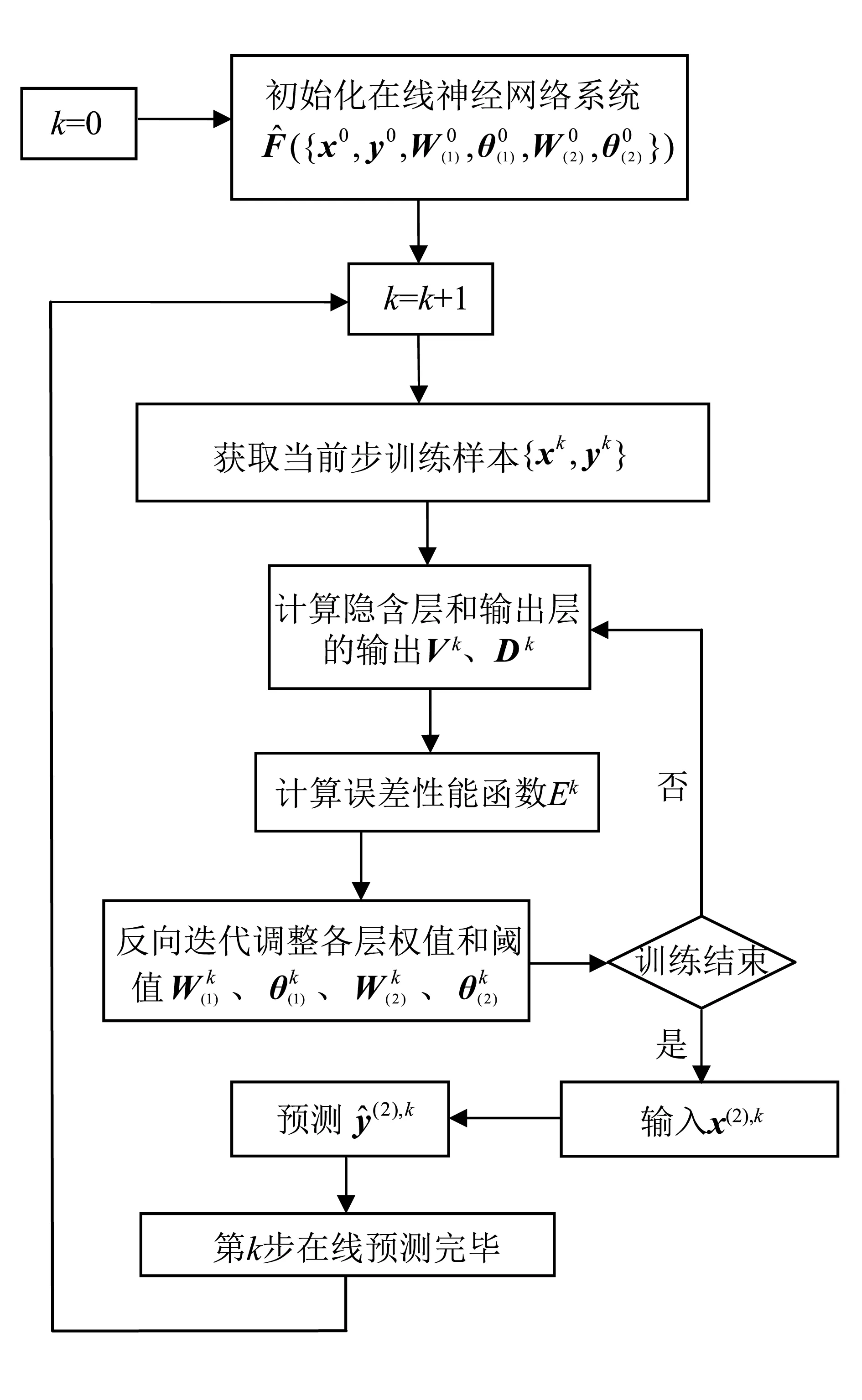
图4 在线神经网络算法流程Fig. 4 Flow chart of online NN algorithm

图5 基于在线NN的混合试验模拟示意图Fig. 5 Schematic of the hybrid testing based on online NN

3.2 基于在线NN的混合试验仿真算例

3.2.1 试验结构及其参数

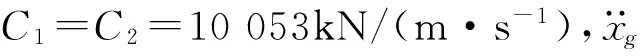
(10)

为了验证本文提出的基于在线NN的混合试验方法的有效性，共进行了三个类型对比试验，分别为：

(1)真实混合试验，采用“Exact”表示。试验子结构与数值子结构采用模型参数真实值，其试验结果作为真实值。

(2)基于离线学习NN的混合试验，采用“Offline-NN”表示。试验子结构采用模型参数真实值，数值子结构的模型采用离线学习方式的神经网络系统，即当前步的恢复力预测所需要的神经网络训练样本为试验子结构加载后获取的所有输入以及输出真实数据。

(3)基于在线学习NN的混合试验，采用“Online-NN”表示。试验子结构采用模型参数真实值，数值子结构的模型采用在线学习方式的神经网络系统，即将当前步的试验子结构的输入和输出数据作为神经网络训练样本来进行恢复力预测。

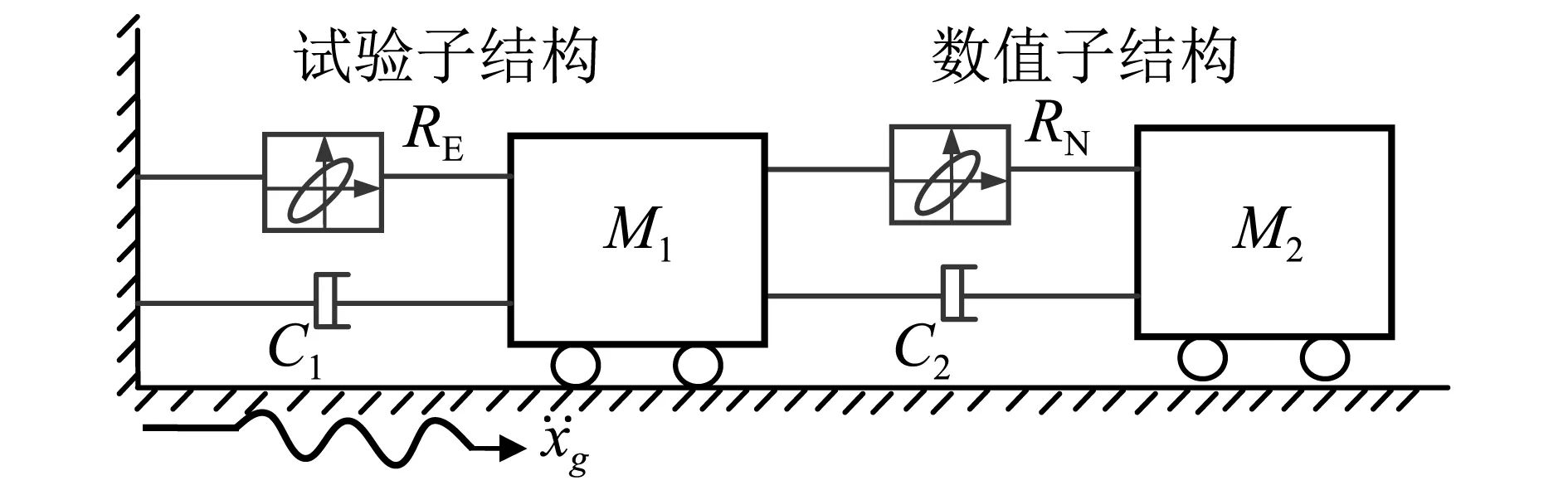
图6 子结构模型示意图Fig. 6 Skeleton of substructure model

3.2.2 选取神经网络输入量及结构

由于Bouc-Wen模型具有较强的非线性关系，为了能够比较全面的模拟滞回模型，采用张健提出的八变量作为神经网络的输入变量，分别为uk、Rk-1uk-1、Rk-1sign(Δuk)、uk-1、Rk-1、ut、Rt和ek-1。其中，下标k为试验加载步数；uk为结构层间位移；Rk-1为结构恢复力；ut和ft分别表示在滞回环转折点处的位移和恢复力；ek-1=(Rk-1+Rk-2)(uk-1-uk-2)/2，ek-1表示滞回系统第k-1步的耗能；sign(Δuk)为第k步位移增量的符号函数。神经网络结构示意图，如图7所示。

采用具有两层隐含层的BP神经网络拓扑结构，每层隐含层具有15个神经元节点，首层激活函数采用双曲正切S型函数，二层激活函数采用对数S型函数。输出层具有一个变量，即结构的恢复力，激活函数采用线性函数。神经网络训练方法选用LM-BP算法，神经网络的训练参数为目标函数采用均方差，Levenberg-Marquardt算法的控制因子μ为0.001，最大训练步数为50步，目标误差设定为10-4。

图7 神经网络结构示意图Fig.7 Skeleton of NN structure

4 结果分析

为了检验基于在线NN与离线NN的混合试验预测效果，图8～图13分别给出了三种类型试验的数值仿真结果对比。图中“Exact”表示真实混合试验；“Offline-NN”表示基于离线学习NN的混合试验；“Online-NN”表示基于离线学习NN的混合试验。

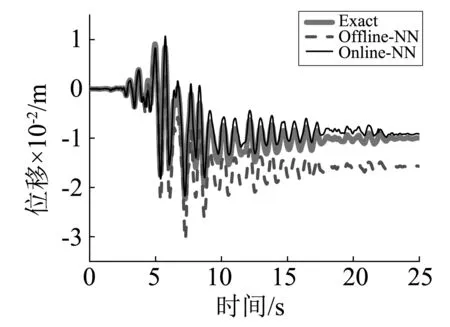
图8 试验子结构位移时程曲线 Fig.8 Displacement curve of testing substructure

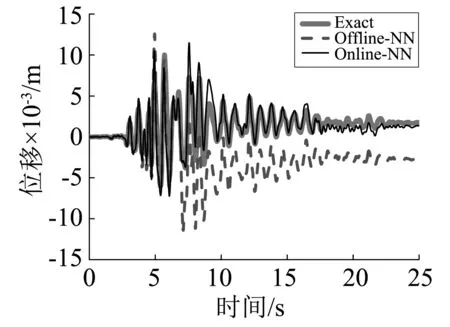
图9 数值子结构位移时程曲线Fig.9 Displacement curve of numerical substructure

图11 数值子结构恢复力时程曲线Fig.11 Restoring force curve of numerical substructure

图12 试验子结构滞回曲线Fig.12 Hysteretic curve of testing substructure

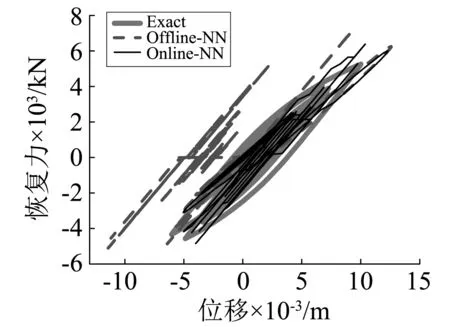
图13 数值子结构滞回曲线Fig.13 Hysteretic curve of numerical substructure

图8和图9分别为试验子结构和数值子结构位移时程反应，可以看出采用离线神经网络得到的位移分别大约在5 s和7 s后开始出现偏移，并且随着时间逐渐增大，而采用在线神经网络得到的位移与真实混合试验结构位移反应吻合较好。图10和图11分别给出了试验子结构和数值子结构恢复力时程反应，可以看出采用离线神经网络与在线神经网络预测的恢复力整体上与真实结构恢复力吻合，但离线神经网络预测的恢复力在地震动峰值附近偏差较大，误差最大约为2 000 kN。图12和图13分别给出了试验子结构和数值子结构的滞回曲线，可以看出采用离线神经网络的试验结果与真实反应存在很大偏差，而本文提出的在线神经网络的试验结果有了很大改善。图14给出了数值子结构恢复力误差对比，结果表明：与离线NN混合试验相比，在线NN混合试验数值子结构恢复力误差明显减小，提高了混合试验精度。

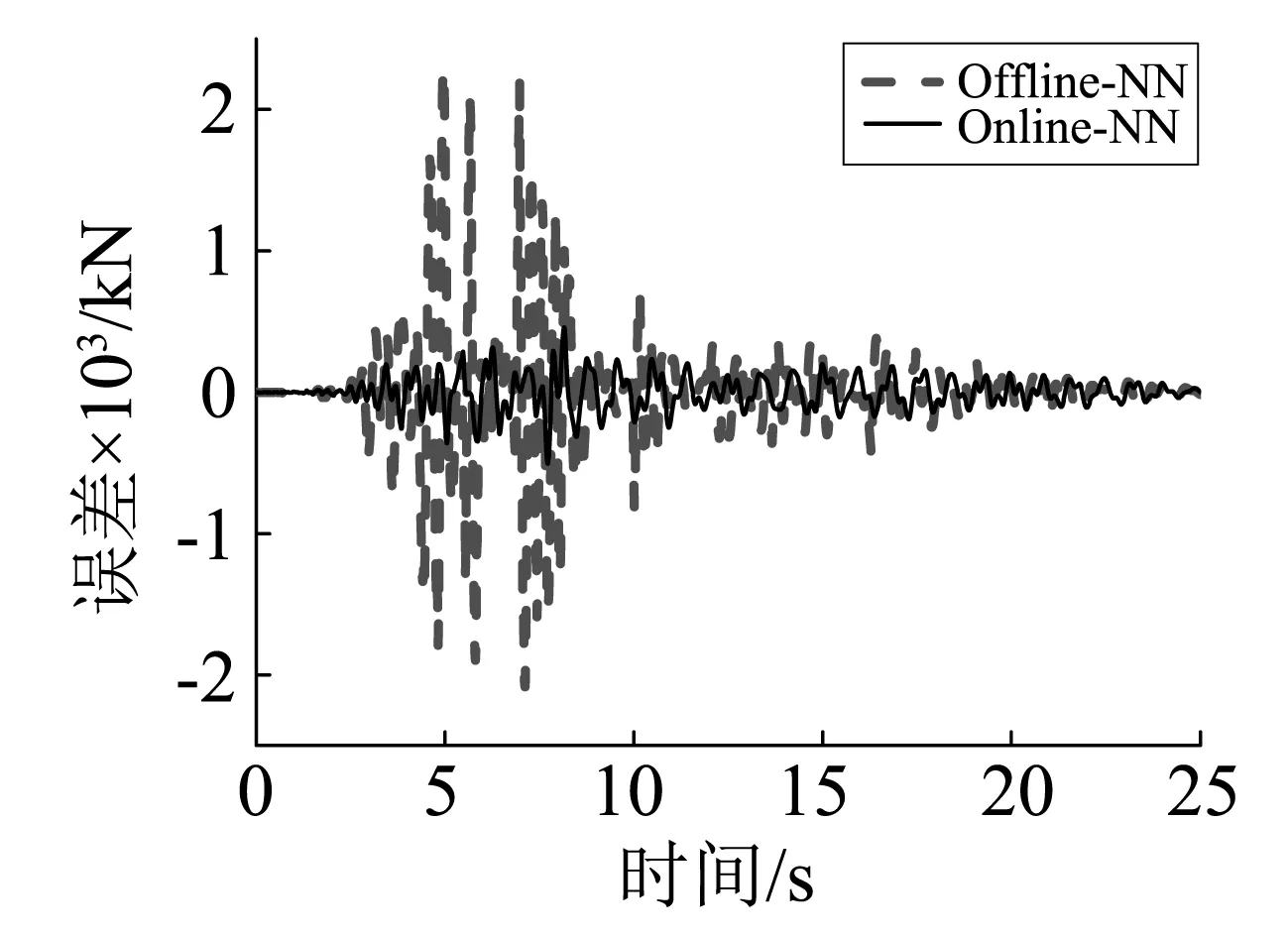
图14 数值子结构恢复力误差对比Fig.14 Comparison of restoring force errors for numerical substructure

为了验证在线NN算法的计算效率，同时记录下基于离线NN和在线NN混合试验数值仿真用时，分别为328.039 s和255.473 s。相对离线算法，在线神经网络算法的计算用时缩短了22%。可见，针对样本数量多且冗余度高的训练集，在线NN算法较离线NN算法具有更快的训练速度，原因在于单个样本收敛所需的迭代次数远小于整个训练集的样本同时收敛的迭代次数。即使在线算法的训练集样本数量大于离线算法，其训练所需得总时间较后者也会大大减少。

另外，为了定量分析试验预测精度，文中选用量纲1的误差指标：相对均方根误差(The Root Mean Square Deviation,RMSD)，数学表达式为

(12)

由于神经网络结构参数中权值与阈值的初始值是系统在较小范围内随机给定的，考虑到每次仿真结果的差异性，笔者通过训练20次后求取平均值作为预测结果。图15给出了在线与离线算法的数值子结构恢复力预测精度对比。

由图15可以看出, 在线NN算法全局误差明显小于离线NN算法，在25 s时在线算法与离线算法相对均方根误差为0.258 61和0.331 52。结果表明：在学习同等数量的样本条件下，在线NN算法的预测精度优于离线NN算法。

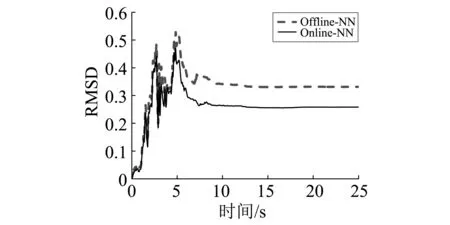
图15 离线与在线NN算法数值子结构恢复力预测精度对比Fig.15 Comparison of prediction accuracy of offline and online NN algorithms

5 结 论

本文提出了基于在线NN算法的混合试验方法，通过两个自由度非线性结构混合试验数值仿真验证了该方法的有效性。试验结果表明，与离线NN算法相比，在线NN算法具有更好的自适应性，能够有效提高恢复力预测精度和计算效率；基于在线NN算法的结构混合试验方法可以提高混合试验结果精度。

目前，神经网络算法在混合试验中的应用仍然有很多方面值得深入研究：

(1)在线神经网络虽然较离线神经网络预测的结果有很大改善，但与结构的真实反应仍存在一定的误差，进一步提高算法精度和计算效率仍是未来研究的重点。

(2)在线算法仍是一种基于前馈型的静态神经网络，利用静态前馈网络对动态系统进行辨识，实际上是将动态时间建模问题变为静态建模问题，需要继续探讨动态神经网络及其在混合试验中的应用。

(3)神经网络系统相对复杂，包含输入与输出变量的选择、隐含层的层数以及节点个数、激活函数的选取、学习率的取值等多方面的影响因素，需进一步研究算法的鲁棒性。

[1] WU B, BAO H, OU J, et al. Stability and accuracy analysis of the central difference method for real-time substructure testing[J]. Earthquake Engineering and Structural Dynamics, 2005, 34:705-718.

[2] JUNG R, SHING P, STAUFFER E, et al. Performance of a real-time pseudo dynamic test system considering nonlinear structural response[J]. Earthquake Engineering and Structural Dynamics, 2007, 36:1785-1809.

[3] 王贞. 实时混合试验的控制和时间积分算法[D]. 哈尔滨: 哈尔滨工业大学, 2012.

[4] 曾聪,许国山,张树伟，等. 力-位移混合控制方法在大型多功能试验加载系统拟静力试验中的应用[J]. 振动与冲击,2016,35(7):161-166. ZENG Cong, XU Guoshan, ZHANG Shuwei, et al. Application of force-displacement hybrid control rnethod in quasi-static tests of a multi-funcaional testing system[J]. Journal of Vibration and Shock, 2016, 35(7):161-166.

[5] WU B, WANG Z, BURSI O. Actuator dynamics compensation based on upper bound delay for real-time hybrid simulation [J]. Earthquake Engineering and Structural Dynamics, 2013, 42(12):1749-1765.

[6] CHANG S. Nonlinear error propagation analysis for explicit pseudo dynamic algorithm[J]. Journal of Engineering Mechanics, 2003,129(8):841-850.

[7] 杨格, 王贞, 吴斌, 等. 建筑结构混合试验平台HyTest开发研究[J]. 建筑结构, 2015,36(11):149-155. YANG Ge, WANG Zhen, WU Bin, et al. Development of HyTest for structural hybrid simulation[J]. Building Structures, 2015,36(11):149-155.

[8] KWON O, KAMMULA V. Model updating method for substructure pseudo-dynamic hybrid simulation[J]. Earthquake Engineering and Structural Dynamics, 2013, 42(13): 1971-1984.

[9] HASHEMI M, MASROOR A, MOSQUEDA G. Implementation of online model updating in hybrid simulation[J]. Earthquake Engineering and Structural Dynamics, 2014, 43(3): 395- 412.

[10] WU B, WANG T. Model updating with constrained unscented Kalman filter for hybrid testing[J]. Smart Structures and Systems, 2014,14(6):1105-1129.

[11] 王涛. 基于模型更新的土木结构混合试验方法[D].哈尔滨:哈尔滨工业大学，2014.

[12] 王涛, 吴斌. 基于UKF模型更新的混合试验方法[J]. 振动与冲击, 2013,32(5):100-109. WANG Tao, WU Bin. Model updating for hybrid testing with unscented Kalman filter[J]. Journal of Vibration and Shock, 2013,32(5):100-109.

[13] WU B, CHEN Y S, XU G S, et al. Hybrid simulation of steel frame structures with sectional model updating[J]. Earthquake Engineering & Structural Dynamiacs, 2016, 45 (8):1251-1269.

[14] 庄镇泉. 神经网络与神经计算机[M]. 北京: 科学出版社. 1996.

[15] 涂建维, 戴葵, 瞿伟廉. 磁流变阻尼器的磁滞效应与神经网络预测调整[J].华中科技大学学报(自然科学版), 2007, 35 (3): 110-112. TU Jianwei, DAI Kui, QU Weilian. Magnetic hysteresis of magnetorheological dampers and its compensation by neural network prediction[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2007, 35 (3): 110-112.

[16] 周大兴, 闫维明,陈彦江,等.神经网络在振动子结构试验中的应用[J].振动与冲击, 2011, 30 (12): 14-18. ZHOU Daxing, YAN Weiming, CHEN Yanjiang, et al. Application of neural network in real-time substructure testing with shaking table[J]. Journal of Vibration and Shock, 2011, 30 (12): 14-18.

[17] YANG W J, NAKANO Y. Substructure online test by using real-time hysteresis modeling with a neural network[J]. Advances in Experimental Structural Engineering, 2004(38): 267-274.

[18] YUN G Y, GHABOUSSI J, ELNASHAI A S. A new network-based model for hysteretic behavior of materials[J]. International Journal for Numerical Methods in Engineering, 2008, 73(4): 447-469.

[19] 张健. 自适应子结构拟动力试验方法[D]. 哈尔滨：哈尔滨工业大学，2010.

[20] MA F, ZHANG H, BOCKSTEDTE A, et al. Parameter analysis of the differential model of hysteresis[J]. Journal of Applied Mechanics, 2004, 71(3): 342-349.

Hybrid testing method based on an online neural network algorithm

Hybrid testing is an advanced structural seismic experimental method that combines the numerical simulation and physical testing and is increasingly being recognized by researchers. One of the challenging issues is how to model the numerical substructure with strong nonlinearity. An online learning neural network (NN) algorithm was proposed based on the conventional offline NN algorithm and applied in the hybrid testing to online predict the restoring force for the numerical structure. Weights and thresholds of the novel algorithm can be updated using a recursive form only based on the current step systematic inputs and observations. Numerical simulations for the hybrid testing based the online and the offline NN algorithms were conducted on a two degrees of freedom nonlinear system. The results show the new online NN hybrid testing method has better adaptation, computational efficiency and prediction accuracy for the detection of restoring force, compared with the offline NN hybrid testing method. In general, the online NN hybrid testing method can effectively improve the accuracy of hybrid testing results.

hybrid testing method; neural network; online prediction; restoring force

黑龙江省青年科学基金项目(QC2013C055); 国家自然科学基金项目(51408157；51308159；51308160)

2016-04-25 修改稿收到日期： 2016-06-06

王涛 男，博士，副教授，1978年生

E-mail: hitwangtao@126.com

TU317

A

10.13465/j.cnki.jvs.2017.14.001

WANG Tao1,2，ZHAI Xuheng2，MENG Liyan2, WANG Zhen3

(1.Institute of Engineering Mechanics, China Earthquake Administration Key Laboratory of Earthquake Engineering and Engineering Vibration of China Earthquake Administration, Harbin 150080, China; 2. School of Civil Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)